一种三自由度弱耦合并联机构运动学分析
2022-10-14谢俊左飞飞杨启志李玉萍
谢俊,左飞飞,杨启志,李玉萍
(1.江苏大学机械工程学院,江苏镇江 212013;2.江苏大学农业装备工程学院,江苏镇江 212013)
0 前言
两平移一转动(Two Translation and One Rotation, 2T1R)并联机构兼顾移动和转动输出特性,在生产实践中应用广泛。毛军华、薛城等人[1-2]研究了2T1R型并联康复机器人;王成军、谢俊、汪志焕等[3-5]将2T1R并联机构应用于物料筛分领域。在机构学研究方面,黄秀琴等[6]对2T1R新构型并联机构进行位置分析;刘延斌、董倩文等[7-8]针对一种3-RPR并联机构分析其运动学特性;邓嘉鸣等[9]研究了(RPa‖3R)-R+RSS型无寄生运动并联机构。在机构耦合研究方面,马履中等[10]研究了三平移弱耦合并联机器人;范彩霞等[11]对完全解耦型2R并联机构进行了运动学分析;TIAN、沈惠平[12-13]等研究了3T1R机构的耦合度和解耦特性。
上述并联机构主要存在两个问题:(1)未兼顾机构耦合度与解耦分析,使得所设计的并联机构不能同时实现运动学分析的简化与控制方式的解耦,不利于机构的快速设计与应用;(2)解耦分析未涉及控制方式耦合程度的判别,输入-输出控制方式的解耦特性不明确。
基于方位特征集理论,本文作者提出一种2T1R并联机构。该并联机构耦合度为1,位置分析所需联立的运动支链数较少;基于位置分析求解动平台工作空间和Jacobian矩阵,在并联机构约束动平台输出三自由度运动的前提下,3种输入-输出控制方式解耦。此外,文中还对该机构速度和加速度进行了研究。
1 并联机构设计及拓扑分析
1.1 机构设计
根据基于方位特征集(Position and Orientation Characteristic, POC)的并联机构拓扑结构设计理论[14],文中提出的2T1R并联机构由动平台1、静平台0和单开链(Single Opened Chain, SOC)Ⅰ、Ⅱ、Ⅲ组成,并联机构的拓扑结构为PRR+2-PRRU。
如图1所示,单开链Ⅰ(P1‖R1‖R2-U1)的结构等价于(P1‖R1‖R2‖R11⊥R12),单开链Ⅱ(P2‖R3‖R4-U2)的结构等价于(P2‖R3‖R4‖R21⊥R22),单开链Ⅲ结构为(P3‖R5‖R6)。静平台0上各移动副轴线布置关系为:移动副P1、P2、P3分别沿x轴、z轴、y轴方向布置,此外,移动副P1、P2、P3轴线两两垂直。

图1 2T1R并联机构结构简图
1.2 机构自由度计算
并联机构的POC方程[14]分别为
(1)
(2)
式中:Msj为支链中第j个子SOC的POC集,j=1,2,…,k;Mbi为第i条支链末端的POC集,i=1,2,…,g;Mpa为机构动平台的POC集。
(1)机构的拓扑结构
如图1所示,组成并联机构的3条单开链Ⅰ、Ⅱ、Ⅲ的拓扑结构分别为
SOC1{-P1‖R1‖R2-U1-}
SOC2{-P2‖R3‖R4-U2-}
SOC3{-P3‖R5‖R6-}
静平台0上,以单开链Ⅲ末端点O′为基点进行分析。
(2)确定各支链POC集
由式(1)可知:
并联机构的全周自由度公式[14]为
(3)
其中:
(4)

(3)确定各支路独立方程数ξLj
该机构可分解为2个独立回路,其组成分别为
SOC1{-P1‖R1‖R2-U1-P3‖R5‖R6-}
SOC2{-P2‖R3‖R4-U2-}
它们的独立位移方程数计算如下:
单开链Ⅰ和Ⅲ组成的子并联机构构成第1个独立回路,由式(4)可得:
ξL1=dim.{Mb1∪Mb3}=
由式(2)可知该子并联机构的POC集:
上述子并联机构与单开链SOC2组成第2个独立回路,由式(4)可得
ξL2=dim.{Mpa(1-3)∪Mb2}=
(4)确定该并联机构自由度
由式(3)可得该并联机构自由度为
因此,该并联机构自由度为3。由驱动副存在准则[14]选取静平台0上P1、P2、P3为驱动副。如图1所示,驱动副P1、P2、P3提供往复直线运动,通过并联机构约束动平台输出2T1R三自由度运动。
1.3 机构耦合度κ分析
由基于单开链单元的机构组成原理[14]可知,任意机构可分解为若干个基本运动链;而ν个独立回路的基本运动链可进一步分解为ν个单开链SOC(Δj) (j=1,2,…,ν),而第j个单开链(SOCj)的约束度定义为
(5)
其中:
式中:mj为第j个SOCj的运动副数;Ij为第j个SOCj的驱动副数。
由∑Δj=0可知,基本运动链的耦合度κ定义为
(6)

耦合度[14]κ与机构构型的复杂程度有关,它反映各运动回路变量间的依赖程度:
(1)当κ=0时,机构基本运动链间完全解耦,其运动学和动力学分析可单独求解。
(2)当κ>0时,机构基本运动链的运动学和动力学分析需联立多个回路求解。
特别的,当κ=1的多回路机构,可用一维搜索法得到位置分析的全部实数解。
第1.2节已计算出2个回路的独立位移方程数,分别为ξL1=ξL2=5,且各回路驱动副数目分别为I1=2、I2=1,由式(5)可知约束度Δ1、Δ2分别为
Δ1+Δ2=0→BKC=1
即该机构基本运动链数为1。由式(6)可知该机构耦合度κ为1,即该机构位置分析的全部实数解可用一维搜索法得到。
2 位置分析
2.1 坐标系的建立
如图2所示,静平台0与动平台1均为矩形,二者平行布置,动平台1位于静平台0正上方,且相距为L0;以动平台1中心P为原点建立动坐标系{P}:P-uvw,且u轴平行于动平台长度方向,并指向A2,w轴竖直向上垂直于动平台,v轴由右手定则确定;同理以静平台0中心O为原点建立定坐标系{O}:O-xyz。设驱动副P1运动量为X,驱动副P2运动量为Z时,动平台与x轴夹角为β,连杆A2B2、连杆B2C2与连杆A3B3与x轴的夹角分别为θR4、θR3和θR5。
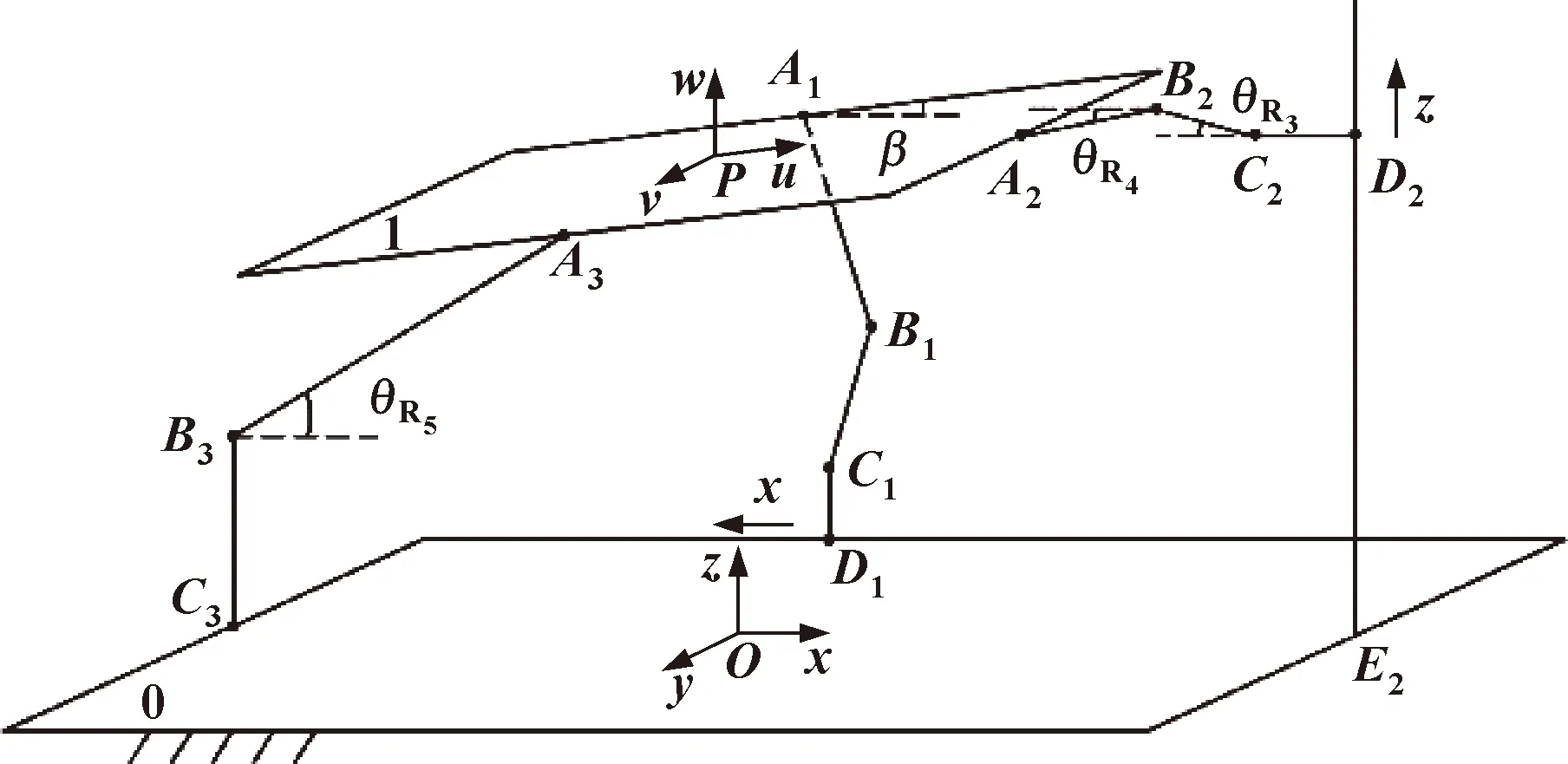
图2 2T1R并联机构运动学模型
该并联机构的结构参数为:静平台0长为2l1,宽为2l2,动平台1长为2l3,宽为2l4;其他尺寸B3C3=l5,A3B3=l6,A2B2=l7,B2C2=l8,C2D2=l9。
2.2 位置正解分析
机构位置正解[15]即已知该机构的输入参数(X,Y,Z),求解动平台的位姿(x,y,β)。
(1)x、y求解
如图1所示,该并联机构运动过程中,移动副P1的移动量即为动平台沿u轴向的移动量,则有:
x=X
(7)
如图2所示,在定系{O}中C3=(-l1,Y,0),B3=(-l1,Y,l5),在动系{P}中A3=(0,-l4,0)。将点A3变换至定系{O}中:
(8)
(9)
进一步,式(9)整理可得:
(10)
(2)β求解
如图2所示,由单开链Ⅱ与单开链Ⅲ在x轴与z轴方向的投影,单开链Ⅰ与单开链Ⅱ在x轴方向的投影组成的封闭回路[16-18],可建立如下方程:
l5+l6sinθR5+l3sinβ=L0+Z
(11)
l6cosθR5+l3cosβ+l7cosθR4+l8cosθR3+l9=2l1
(12)
l9+l8cosθR3+l7cosθR4+l3cosβ=l1+X
(13)
将式(13)整理为l8cosθR3+l7cosθR4=l1+X-l9-l3cosβ,并代入式(12)中,整理可得:
(14)
进一步,将式(14)各式平方后相加可得:
(15)
进一步,整理式(15)可得:
Asin2β+Bsinβ+C=0
(16)
其中:
解式(16)可得:
(17)
即有:
β=arcsinU
(18)
2.3 位置反解分析
机构位置反解即已知动平台位姿(x,y,β),反求该机构的输入参数(X,Y,Z)。
(1)X、Y求解
(19)
(2)Z求解
由式(15)可知:
(L0+Z-l5)2+d(L0+Z-l5)+e=0
(20)
其中:
解式(20)可得:
(21)
即有:
Z=u+l5-L0
(22)
2.4 位置分析算例
设并联机构结构参数为:l1=400 mm,l2=370 mm,l3=150 mm,l4=75 mm,l5=185 mm,l6=560 mm,l7=165 mm,l8=60 mm,l9=210 mm,L0=415 mm。根据三维建模与实际装配情况,式(10)与式(21)中的符号“±”选“+”,式(17)与式(19)中的符号“±”选“-”,通过MATLAB[19-20]验证所得位置正反解方程正确性。仿真步骤如下:
(1)设置输入参数(X,Y,Z);
(2)将输入参数(X,Y,Z)代入正解模型,计算得正解参数(x,y,β);
(3)将正解参数(x,y,β)代入反解模型,计算得反解参数(X′,Y′,Z′);
(4)计算所得反解参数(X′,Y′,Z′)与输入参数(X,Y,Z)的差值;
(5)根据差值判断位置分析正确性。
经上述仿真步骤,可得位置分析算例,如表1所示:由正反解方程所得的反解参数(X′,Y′,Z′)与输入参数(X,Y,Z)差值为0,即所得位置正反解方程正确。

表1 位置分析算例
3 工作空间
工作空间即满足约束条件的机构末端参考点集,假设杆件在运动过程中不发生干涉,基于运动学正解,使用极限边界法求解机构工作空间,具体步骤如下:
(1)根据第2.4节设置机构尺寸参数;
(2)设定驱动副输入参数(X,Y,Z)的搜索区间为X∈[-100 mm,0],Y∈[-250 mm,250 mm],Z∈[-150 mm,150 mm];
(3)由几何约束,求解约束方程:
(4)将步骤(1)和步骤(2)代入位置正解方程中,求解动平台位姿参数,并由步骤(3)所示的约束条件对位姿参数进行筛选。
依次重复步骤(1)—步骤(4),并以步长ΔX、ΔY、ΔZ在驱动副行程内进行搜索,当到达驱动副行程边界时结束,最后利用MATLAB软件记录并输出所有满足约束条件的点集,所得机构三维工作空间如图3所示。
由图3和图4可知,在X∈[-100 mm,0]范围内,y-β截面工作空间凹凸有界,边界内部区域连续无空洞。随着x值的增大,截面面积朝y轴正向逐渐增大。

图3 并联机构三维工作空间

图4 工作空间y-β截面
4 解耦分析
4.1 耦合类型判断
解耦即机构某方向的运动仅受特定方向的驱动影响,而其他方向的驱动不影响该方向的运动[21]。随着运动支链的增多,机构耦合性增强,进而影响机构的控制,降低运动精度,因此解耦分析是必要的。
(23)
整理式(23),基于Jacobian矩阵可得如下形式:
(24)
式中:Jp和Jq分别为该并联机构的正、逆Jacobian矩阵。
且有:
Jp=
根据耦合特性,GOGU[22]将并联机构分为4类:
(1)完全同性并联机构:Jacobian矩阵J为对角矩阵,且对角元素相同;
(2)去耦并联机构:Jacobian矩阵J为对角矩阵,但对角元素不同;
(3)解耦并联机构:Jacobian矩阵J为三角矩阵;
(4)若非上述三类,则为耦合并联机构。
由第1.2节和第2.1节可知,该并联机构沿x、y、z轴的直线移动输入(X,Y,Z)产生沿x、y轴的平移和绕y轴的转动,使动平台输出三自由度运动(x,y,β)。在保证动平台输出运动(x,y,β)的前提下共有7种输入-输出控制方式:
(1)X-x,即保持输入(Y,Z)不变,改变输入X,研究输入X与输出x间的对应关系。
(2)Y-y,即保持输入(X,Z)不变,改变输入Y,研究输入Y与输出y间的对应关系。
(3)Z-β,即保持输入(X,Y)不变,改变输入Z,研究输入Z与输出β间的对应关系。
(4)(X,Y)-(x,y),即保持输入Z不变,改变输入(X,Y),研究输入(X,Y)与输出(x,y)间的对应关系。
(5)(X,Z)-(x,β),即保持输入Y不变,改变输入(X,Z),研究输入(X,Z)与输出(x,β)间的对应关系。
(6)(Y,Z)-(y,β),即保持输入X不变,改变输入(Y,Z),研究输入(Y,Z)与输出(y,β)间的对应关系。
(7)(X,Y,Z)-(x,y,β),即同时改变输入(X,Y,Z),研究输入(X,Y,Z)与输出(x,y,β)间的对应关系。
由式(24)中的Jp可知,该并联机构J矩阵属于非对角、非三角矩阵,该机构为耦合并联机构,即存在耦合输入-输出控制方式。
4.2 控制方式解耦分析
由式(24)的Jp可知,正Jacobian矩阵Jp的列反映输入-输出参数的映射关系。为进一步研究机构控制方式的解耦特性,根据Jacobian矩阵列的相关性[23]可知:
(25)
式(25)表示第i列与第j列向量所代表的输入-输出控制方式线性无关,即无耦合;
(26)

(27)
若G为对角矩阵,则机构输入-输出控制方式完全解耦;反之则存在耦合,对应输入-输出控制方式具有相关性。由式(27)可知:


5 速度与加速度正解分析
5.1 速度正解公式推导
当机构不存在奇异位置时,即Jp可逆,由式(24)可知,该并联机构速度正解[24-25]为
(28)
5.2 加速度正解公式推导
将式(24)中各变量对时间求一阶导数,可得:
(29)
其中:

当机构不存在奇异位置时,即Jp可逆,则该并联机构加速度正解为
(30)
5.3 速度与加速度仿真

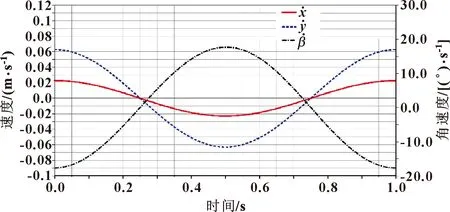
图5 动平台速度ADAMS仿真曲线

图6 动平台加速度ADAMS仿真曲线
由图5和图6可知:该并联机构速度与加速度曲线变化平稳,无尖点,具有良好的动力学性能。
6 结论
(1)基于拓扑结构设计理论,提出一种新型2T1R弱耦合并联机构,可实现动平台沿x轴、y轴的平移和绕y轴的转动。
(2)该并联机构耦合度为1,降低了机构位置正解的求解难度,通过MATLAB仿真对比反解参数与输入参数,二者差值趋于0,体现了位置分析的合理性。
(3)基于位置正解分析该机构的工作空间,发现其工作空间连续无空洞。
(4)基于Jacobian矩阵列的相关性,推得该机构平动输入Y与平动输出x间存在耦合,3种输入-输出控制方式X-x、Z-β和(X,Z)-(x,β)解耦。
(5)速度与加速度曲线变化平稳且无尖点,表明该并联机构具有较好的动力学性能。
