变系数时滞脉冲方程周期解的指数稳定性研究

雷 婷， 朱 双

(西南交通大学 数学学院，成都 610031)

0 前 言

神经网络属于复杂网络，因其能够描述各种真实的系统而受到了大量学者研究，从Gohe和Grossberg提出Gohe-Grossberg神经网络系统以来，稳定性一直是复杂网络的重要问题，神经网络通常用微分方程进行建模，而Halanay不等式是研究系统稳定性的重要不等式。

由于神经网络是多样性的，研究其稳定性或者同步性时，采用的不等式存在差异。传统的Halanay不等式已不能满足需求，许多学者对Halanay不等式及其广义形式[1-5]进行了研究，得到了许多有用的结论[6-9]。

则存在γ>0，K>0使得

f(t)≤Ke-γ(t-t0)，t≥t0

传统的Halanay不等式系数为常数，要求衰减因子必须时刻大于增长因子，Liu Bo在文献[4]将其系数推广为变量

D+表示Dini导数，a(t),b(t)是一般标量函数，当τ较小时，可以从时间平均函数条件导出其解渐进稳定性，不用时刻满足衰减因子大于增长因子。

Lin Yusen在文献[4]的基础上加入脉冲因素[10]

得到的不等式可以用于不连续的系统的稳定性证明。上述工作最后的结论均与时滞的取值大小有关系。

由于信息传播时存在多种路径，沿着这些传播路径会产生不同的现象，时滞不能用瞬时或者离散来描述，因此出现了一种更为合适的时滞类型——连续的分布时滞[11]。同时，在物理，电子学，信息科学等领域中，信息的传递会在某一时刻由于环境或者其他因素突然发生变化，导致系统的状态发生变化，产生脉冲效应[12]。文章均没有研究不等式同时含有变系数，脉冲以及分布时滞型的情形，故将Halanay不等式的时滞推广为分布时滞，常系数推广为变系数，并加入脉冲因素，研究了脉冲分布时滞神经网络系统周期解的稳定性问题。

考虑如下脉冲分布时滞微分不等式形式

利用常数变异法对不等式进行证明，证明不等式的关键在于确定适当的指数。由于影响因素包含分布时滞，脉冲，变系数，不便使用传统的反证法，故文章将指数的取值和系数周期性结合起来。分布时滞，脉冲，变系数满足下文假设A(1)，得到的指数和时滞脉冲，变系数均有关系。不分别考虑每一个因素的影响，而是考虑整体的影响。

神经网络是多样性的，研究其稳定性或同步性时，采用的方式存在差异。文献[14]利用微分积分型不等式证明了时滞神经网络系统的全局稳定性，文献[15]利用含有离散时滞和脉冲类型的不等式证明了转换系统的稳定性，均利用不等式证明系统的稳定性。使用新建立的含有分布时滞和脉冲的变系数广义Halanay不等式证明脉冲时滞方程的指数稳定性，利用广义Halanay不等式和Banach不动点理论，建立简单的Lyapunov函数，得到了使脉冲神经网络系统周期解的存在性和指数稳定性的充分条件，具有较强的实用性。

1 预备知识

在这一节中，为了证明广义的Halanay不等式，给出表示方法。

C(X,Y)表示从拓扑空间X到拓扑空间Y的连续映射。PC(J,H)={ψ(t):J→H}，ψ(t)在可数个点(s∈J)外是连续的，s∈J时左右极限存在且相等。J⊂R是间隔的集合，H是一个完备的度量空间。特别的，PC≜PC([-τ,0],Rn])。

考虑下列含有脉冲和分布时滞的微分不等式

x(t)≥0在t≥t0是连续函数，φ∈PC,α(t),β(t)≥0 是周期为T的周期函数，对于任意的k∈N，存在q使得tk+q=tk+T，pk+q=pk，pk是正常数。

2 主要结果

给出下列假设

接下来，提出引理1并对引理1进行证明。

引理1 对于任意0<ε<1，x(t)是下列微分方程的一个解

(1)

x(t)≤K1([φ]τ+ε)eλ(t-t0)+εG1

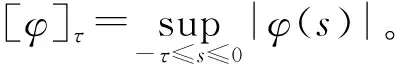
证明采用常数变异法，当t>t*≥t0时

x(t)=W1(t,t*)x(t*)+

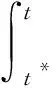
因为x(t)≥0,β(t)≥0,t≥t0

当t>t*≥t0时，x(t)≥W1(t*,t)x(t*)

当t≥t0+τ时，x(t)≥W1(t-τ,t)x(t-τ)

则x(t)≤W1-1(t-τ,t)x(t-τ)

从式(1)可知

利用Grownwall不等式，当t≥t0+τ

(2)

其中

由式(2)可知

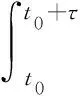
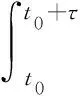
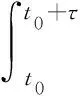
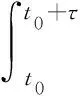
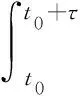
结合式(2)当t≥t0+τ

x(t)≤MW2(t0,t)([φ]τ+ε)+

(3)

其中

τ)(β(s)+1)ds

对于t∈[t0+nT,t0+(n+1)T],n=0,1,2,…

由式(3)结合式A(1)可得：

x(t)≤M([φ]τ+ε)[W2(t0,t0+T)]nW2(t0+nT,t)+

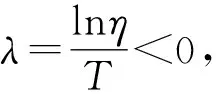
x(t)≤M([φ]τ+ε)enλTW2(t0,t-nT)+

M([φ]τ+ε)enλTeλ(t-t0-nT)e-λTW2(t0,t-nT)+

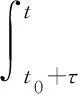
(4)

当t∈[t0+τ+nT,t0+τ+(n+1)T],n=0,1,2,… 时

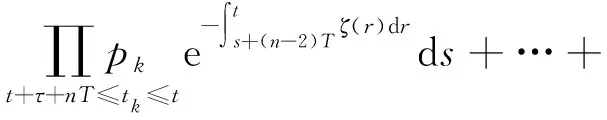
(ηn-1+ηn-2+…+η+2)(B+1)2θT:=G1<∞

(5)

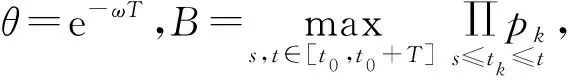
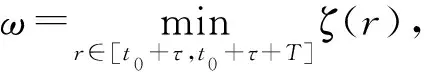
当t≥t0+τ时

x(t)≤K([φ]τ+ε)eλ(t-t0)+εG1

表明存在正数K1,G1，独立于ε，当t≥t0

x(t)≤K1([φ]τ+ε)eλ(t-t0)+εG1

证毕。

u(t),v(t)∈PC[[-τ,∞],]满足

且

则

u(t)≤v(t),t0-τ≤t≤t0

即

u(t)≤v(t),t≥t0。

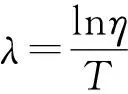
x(t)≤K([φ]τ+ε)eλ(t-t0)

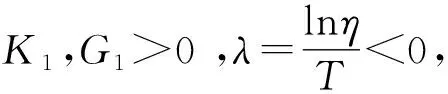
x(t)≤K1([φ]τ+ε)eλ(t-t0)+εG1

当ε→0时

x(t)≤K([φ]τ+ε)eλ(t-t0)

则结论成立。

3 神经网络周期解的指数稳定性

神经网络属于复杂网络范畴，复杂网络可以描述各种真实的系统，如生态系统，互联网，生物神经网络，社会网络，生物分子网络等[16-18]，而神经网络的稳定性是研究神经网络的重要问题，因此大量学者研究了神经网络系统的稳定性[19-20]，常用的方法分为两大类：构造Lyapunov泛函法(Lyapunov直接法,Lyapunov-krasovskii方法, Lyapunov-Razumikhin方法)、矩阵及不等式法(Laselle不变集、线性矩阵不等式、微分不等式、积分不等式)。文章采用的是不等式法，避免了构造复杂的Lyapunov函数，只需构造简单Lyapunov函数即可。研究以下神经网络的周期解的指数稳定性问题：

(6)

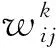
φ(t)=[φ1(s),…,φn(s)]T∈PC。

通过(t0,φ)的解为y(t,t0,φ)或yt(t0,φ)，其中

yt(t0,φ)=y(t+s,t0,φ),-τ≤s≤0,t≥t0。易知，系统式(6)有唯一解y(t,t0,φ)。则系统式(6)可以被称为神经网络系统。下面考虑这个神经网络的周期解的存在惟一性，在此之前给出下列引理。

引理3 式(1)有周期解当且仅当存在φ∈PC满足

yt+T(t0,φ)=φ

定理2假设存在非负常数Fj,Gj,j=1,…,n使得

|fj(x)-fj(y)|≤Fj|x-y|

|gj(x)-gj(y)|≤Gj|x-y|,∀x,y∈R

η(t),ξ(t)满足

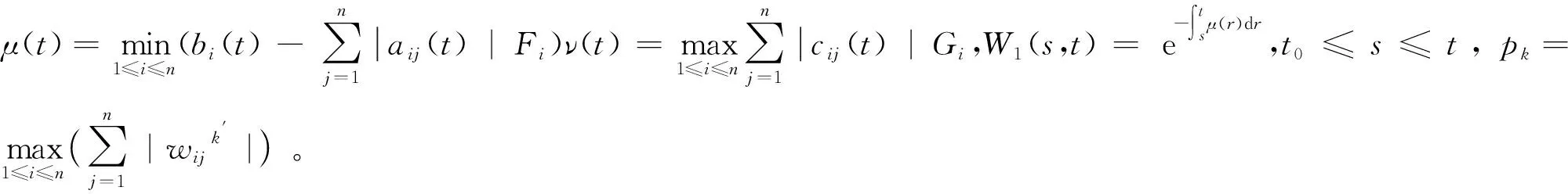
则式(6)有惟一全局稳定周期解。

证明令φ，φ∈PC，x(t),y(t)是上述系统通过初值(t0,φ)和(t0,φ)的解，则有

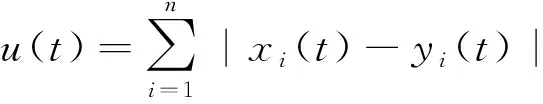
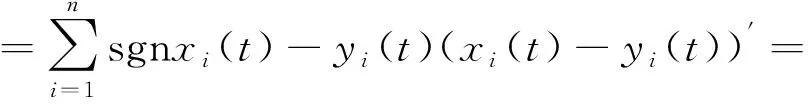
当t=tk时

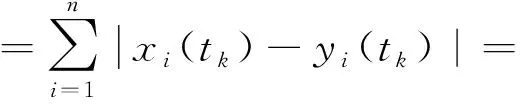
由引理1、引理2和定理1可得

u(t)≤Keλ(t-t0)，t≥t0，λ<0

定义算子F：PCt0→PCt0+T有Fφ=yt0+T,φ∈PCt0

由周期性可知PCt0=PCt0+T，即F将PCt0映射到自身。进一步可知，式(6)的存在惟一解

F*φ=xt0+kT(t,φ)，k∈

由于u(t)≤Keλ(t-t0)，t≥t0则

||Fmφ-Fmφ||=||yt0+mT(t0,φ)-xt0+mT(t0,φ)||

其中，m∈N,0

结合引理3可得式(6)的一个全局指数稳定周期解x(t,t0,φ*)，证毕。

4 结束语

建立了一个新的具有脉冲和分布时滞的变系数广义Halanay不等式，分析了神经网络系统式(1)的稳定性，由分析结果可知式(1)的周期解指数稳定。分布时滞在应用中十分广泛，例如生态系统中捕食者和被捕食者的关系不仅跟过去某一时刻有关系，而且跟过去某一段时间有关系，分布时滞可以很好描述这一现象。此外，将常系数改为变系数克服了系数为常量时衰减因子必须时刻大于增长因子的弊端。

神经网络系统可以描述各种真实的系统。例如：生态神经网络，互联网，社会网络等等。而系统的稳定性关系到一个系统性能的好坏，建立广义Halanay不等式可以用于各种系统的稳定性分析。各类广义Halanay不等式最后的结论都依赖于时滞，若能证明Halanay不等式最后的结论不依赖于时滞，则将是一个更优的结论。