双馈风机系统最大功率控制研究

2022-10-13张吴飞王双园李帅帅李嘉成

重庆工商大学学报（自然科学版） 2022年5期

张吴飞，王双园，李帅帅，李嘉成

(上海理工大学机械工程学院，上海 200082)

0 引言

传统的最大风能追踪是以风力发电机输出的机械功率最大为目标，忽略齿轮箱等带来的损耗，而双馈电机的输入功率即为风力机输出机械功率。刘凯等[1]通过模糊控制对电机进行阻尼控制，发现模糊控制能够对电机进行较好的控制。孔旻玥等[1]通过矢量与虚拟同步机分别控制，进行建模和分析，整个功率点寻优系统较为精确，但响应时间不足。李爽等[3]通过PSO算法进行PID控制，整个控制的抗干扰性能显著提高，但反应时间仍然较长，灵敏度还不够。颜湘武等[4]通过遗传算法解决了双馈电机故障穿越问题，但仍然存在寻优耗时较长的问题。秦继朔等[5]通过寻优算法辨识调节器参数。Cheng X等[6-7]通过高灵敏度待辨别，低灵敏度不辨别的方法辨识参数。以上研究虽成功解决了灵敏度问题，但却牺牲了一部分抗干扰性，当风速在复杂变化时，往往会使得RMS波动较大。Wang Y等[8-9]通过WECC Type-4型风机的模型，筛选出电气参数进行识别，可以较精准地识别到最大功率点，但波动性较大。本文摒弃传统以风力机输出机械功率最大建模而改用以双馈电机定子输出反馈给电网的功率最大为目标建立DFIG数学模型，根据此数学模型引入模糊控制，从而实现双馈电机最大功率点响应迅速，寻优稳定的跟踪策略。

1 最大功率点跟踪策略

1.1 基于电网电压定向下DFIG的数学模型

(1)

其中，Us为电网电压矢量的幅值，usd和usq为dq轴上定子电压分量。

由于双馈电机的定子侧输出是直接与电网相连接的，因此当电网电压保持不变，定子磁链在旋转dq坐标系下的分量是保持不变的，即使变化，也只是一个小的波动;而且，由于定子电阻值比较小，因此忽略定子绕组产生的电动势，定子电压的方程式为

(2)

将式(1)代入式(2)，可以得到：

(3)

可见，定子磁链完全落在了q轴上，d轴上的分量为0，定子输出电压与定子磁链互相垂直。将式(3)代入定子磁链方程(定理方程不过多阐述)可得：

(4)

将式(4)和转子磁链方程联立(定理方程不过多阐述)，得：

(5)

其中，ψsq、ψsd、ψrd、ψrq为dq轴上定、转子磁链的分量；isd、isq、ird、irq为dq轴上定、转子电流的分量；Lm为同轴定、转子绕组在dq坐标系下的自感；Ls为两相定子绕组在dq坐标系下的自感；Lr为两相转子绕组在dq坐标系下的自感。

(6)

由式(6)可见，双馈电机转子侧的磁链在dq轴上的分量可单独由dq轴上转子电流分量来进行控制。

再将式(6)代入转子电压方程可得：

urd=Rrird+pψrd-ωsψrq

(7)

urq=Rrirq+pψrq+ωsψrd

(8)

(9)

通过对双馈电机转子电压方程的简化，转子电压将无需用定子电流量来表示，虽然转子电压之间还是存在耦合，但是通过前馈补偿的方法，可以实现转子dq轴之间的解耦控制。

将式(3)、式(4)代入转矩方程(定理方程不过多阐述)，可得简化后的转矩方程:

(10)

其中，Te表示电磁转矩，np表示极对数，而有功、功率Ps、无功功率Qs计算公式为

(12)

由式(12)可见，通过电网电压定向以后，定子输出的有功功率Ps可以由转子电压的d轴分量ird单独控制，而无功功率Qs则由电流irq单独控制，进而对有功、无功解耦控制。因此，可以通过改变转子电流的转矩分量实现双馈电机最大功率点跟踪策略。

1.2 最大功率点跟踪

当忽略铁芯损耗和所有杂散损耗时，定子的铜损耗将影响定子向电网的输出功率。图1为双馈电机内部功率流向图，由于当双馈电机的转速处于超同步或亚同步时，电机转子的功率流向是不同的，因此图1(a)为亚同步速时的功率流向图，转子此时处于电动状态;图1(b)为超同步速时的功率流向图，此时转子侧进行发电。

(a) 处于亚同步速状态

(b) 处于超同步速状态图1 双馈电机内部功率流向图Fig.1 Internal power flow diagram of doubly-fed motor

图1中Pr、Per、Pcur分别为转子侧输入电功率、转子侧电磁功率和转子侧铜耗；Ps、Pes、Pcus分别为定子侧输出功率、定子侧电磁功率和定子侧的铜耗；Pmech为双馈电机轴上输入的机械功率，由于忽略了机械转轴上的损耗，因此双馈电机的电磁功率Pe=Pmech，所以:

(13)

根据功率的流向图，双向电机定子输出有功功率Ps等于定子侧的电磁功率Pes减去定子侧的铜耗Pcus：

Ps=Pes-Pcus

(14)

将式(13)代入式(14)，则：

(15)

对式(12)进行变化，可得：

(16)

将定子电流的表达式(16)代入式(15)可得：

(17)

定子输出有功功率Ps的值与无功功率Qs、双馈电机的输入功率Pmech,和双馈电机的电角速度ωr有关。Ps的大小取决于Qs,、Pmech和ωr这3个变量的值。由于Pmech即为风力机输出的机械功率，因此Pmech和ωr的关系满足图2风力机输出功率-转速曲线图,ωr=Nωwnp/9.55，N为齿轮箱增速比。

图2 同一风速下风能曲线Pmech及定子输出功率曲线PsFig.2 Wind energy curve Pmech and stator output power curve Ps at the same wind speed

1.3 无功功率的取值

无功功率Qs影响着有功功率Ps的值，因此为了研究双馈电机的最大功率点跟踪策略，必须对双馈电机定子输出的无功做分析。在分析无功之前，首先对双馈电机内部的损耗做一定的分析。因为忽略了电机的铺铁芯损耗和一切内部杂散损耗，因此：

(18)

当双馈电机内部损耗最小时，此时定子侧的输出无功功率为

(19)

当Ploss的值为最小时，定子无功输出Qs只与电网以及电机的参数有关，与双馈电机的运行状态以及励磁电流大小无关，所以当电网电压恒定，忽略一切由于外界环境变化或者电机高速运行引起的电机参数变化的因素，则双馈电机内部损耗最小时，定子输出无功功率为一恒定值。

本文将以双馈电机内部损耗最小为目标，得到最佳的无功功率给定值。由于通过电网电压定向，实现了双馈电机发电时定子输出有功、无功功率的解耦控制，因此根据式(12)，单独控制转子电流q轴分量irq,可以控制无功Qs的大小。

1.4 最大功率点跟踪曲线

通过式(19)确定了无功功率Qs的值，再通过式(17)可以计算得到双馈电机定子反馈给电网的功率Ps的大小，每一组(Pmech,ωr)可以确定一个Ps的值。而(Pmech,ωr)可以根据风力机输出功率和转速变化之间关系，计算出不同风速变化下，双馈电机定子反馈给电网功率Ps的大小，Ps的变化如图3所示。

图3 11 kW双馈电机定子反馈电网功率变化曲线Fig.3 Power variation curve of 11 kW doubly-fed motor stator feedback grid

2 基于模糊控制器的控制策略

2.1 模糊控制器设计

将上述提出的最大功率点跟踪策略与模糊控制原理相结合，建立最大功率追踪模糊控制器，通过调节双馈电机的转速来实现最大功率发电的目标[2]。如图4所示为模糊控制器框图。

图4 模糊控制器框图Fig.4 Block diagram of fuzzy controller

图4中KWR和KPO为发电机转速ωr的量化因子，KWR和KPO的产生是通过模糊计算得到的，他们的值随转速的增加而增加。当确定了速度的隶属度之后，利用量化因子计算规则表，得到相应的KWR和KPO的值。

(a) Δpo(pu)

图5 模糊变量的隶属度函数Fig.5 Membership function of fuzzy variables

2.2 最大功率点追踪控制策略

经过电网电压定向，实现了对双馈电机定子侧输出功率的有功、无功解耦控制，再利用定子输出有功Ps曲线具有单峰特性，通过最大功率追寻模糊控制器，搜索到最大功率处的电机转速，进行转速闭环控制，从而实现了双馈电机最大功率馈电控制。

在整个双馈风力发电系统中，核心部分是控制算法。当系统实现并网控制，则下一步要进行最大功率追踪控制，从而实现整个机组的最优状态发电。因此，控制策略的正确性将影响整个发电系统的运行状态及性能。本文选择使用模糊控制器，也是为了能使整个机组响应速度快、抗干扰性能强。

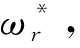
3 仿真与实验

为验证最大功率追踪控制策略的正确性，在MATLAB/Simulink环境下搭建仿真模型，进行仿真验证。仿真所使用的双馈电机参数为:额定功率P=11 kW,极对数np=3,，定子电阻Rs=1.95 Ω，定子自感Ls=0.267 H，转子电阻Rr=1.45 Ω，转子自感Ls=0.267 H，互感Lm=0.258 H，参数均已折算到定子侧，定、转子都为Y型连接。

风速为6 m/s及8 m/s，双馈风力发电系统运行在最大功率点时，双馈电机的运行参数见表1。

表1 最大功率点的运行参数Table 1 Operating parameters of maximum power point

图6(a)、图6(b)、图6(c)，分别为风速6 m/s时，双馈电机的转速、电磁转矩和定子侧反馈给电网功率曲线图。由于在追寻最大功率点前，先要实现双馈电机的并网控制策略，因此仿真的0.2 s前为并网控制，此时定子尚未与电网相连，认为此时的Ps=0 W。

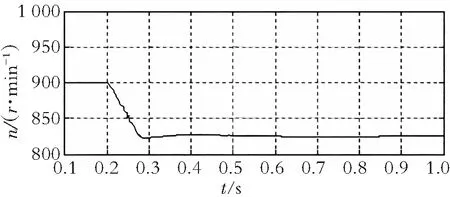
(a) 双馈电机转速

(b) 双馈电机转矩

在稳定风速下，双馈风力发电系统通过模糊控制器的在线搜索，能稳定运行在最大功率馈电状态，下面将通过仿真验证风速从6 m/s变化到8 m/s时，系统能否始终追踪最大功率。如图7所示为风速变化下双馈电机的运行参数。

(a) 双馈电机转速变化曲线图

(b) 双馈电机转矩变化曲线图

(d) 双馈电机定子输出电流的变化曲线图

(e) 双馈电机转子侧电流变化曲线图图7 风速变化下双馈电机运行参数Fig.7 Operating parameters of doubly-fed motor under wind speed change

如图7(a)、图7(b)所示，0.6 s处风速变化，整个发电系统具有较强的动态调节能力。双馈电机能快速地稳定运行在最佳转速，电磁转矩的调节响应时间较短，超调量较小，系统的鲁棒性好。图7(c)所示的定子输出功率Ps的值从2.8 kW变化到6 kW，与表1 的最大输出功率数据基本吻合，说明双馈风力发电系统风速变化前后始终稳定运行在最大功率输出点，最大功率追踪控制策略是正确的。

而定子输出无功Qs的值在风速变化前后都稳定在775 W上下，实现了有功、无功的解耦控制。图7(d)为定子侧的输出电流曲线，由于实现并网后，双馈电机定子与电网相连，因此风速的变化只会造成定子电流幅值的变化，频率始终为工频50 Hz。图7(e)为双馈电机转子励磁电流变化曲线，通过对励磁电流频率、幅值、相位的调节，达到双馈电机变速恒频、并网控制、最大功率追踪控制等目的。

图8为模糊控制器在风速变化时输出转速变化曲线图。在风速变化前后，模糊控制器的响应时间较短，能快速地搜索到不同风速下的最佳转速，虽然转速值有一定的超调量，但是不会影响系统的稳定性。