基于改进的FCM算法对图像分割的研究和应用

朱 凯 俊

(安徽理工大学 电气与信息工程学院，安徽 淮南 232001 )

0 引 言

随着人类社会的发展，大数据时代的来临，如何从一张包括海量信息的图片中提取自己想要的部分信息成为当前人们需要解决的问题。图像分割的核心是聚类，即把所有样本数据有规律划分到各个类当中。1965年，美国学者 Zadeh[1]教授首次在 Fuzzy Sets 中提出一种描述模糊现象的概念——模糊集合(Fuzzy Set, FS)，这一概念的出现使得使用数学思维和方法处理问题的现象有了理论依据，构成了模糊数学的基础；1969 年，Ruspini[2]利用模糊集理论简化数据表示，在聚类分析中运用模糊集的思想，首次提出了模糊聚类方法；1973 年，Dunn[3]给出了一个将硬 C 聚类算法与模糊理论相结合的特例，首次提出FCM 算法；1984年，Bezdek[4]将 Dunn 算法扩展到m>1 的情形，使用隶属函数矩阵对算法进行了改进，并评估了提出的方法，验证了算法的收敛性，模糊 C 均值算法逐渐形成了较完整的体系。

1 理论基础

1.1 直觉模糊集

直觉模糊集合与模糊集合最大的差别在于1965年Atanassov在直觉模糊集中引入了非隶属度概念。下面给出直觉模糊集定义[5]：

集合X={x1,x2,…,xn}上的一个直觉模糊集可以表示为

A={〈xi,uA(xi),νA(xi)〉∣xi∈X},i=1,2,…,n

其中，函数值uA(xi),νA(xi)都在闭区间0到1上取值，它们表示的是元素xi对A的隶属度和非隶属度，所以它们的和也在闭区间0至1上取值，并且他们的差值|uA(xi)-νA(xi)|∈[0,1]。规定πA(xi)=1-uA(xi)-νA(xi),函数值πA(xi)为犹豫度，且也在闭区间0到1取值。

1.2 直觉模糊熵

熵反映的是体系混乱程度的度量，模糊信息熵反映的是模糊时间段的信息量，熵值越大，则表示信息种类越多样化。这一概念于1972年被Burillo在信息熵的基础上进行拓展并提出[6]。之前人们提出的一些直觉模糊熵测度存在一些明显的缺陷，比如：

能很清楚地看出这个模糊熵测度里面没有包含犹豫度对直觉模糊不确定程度的影响。所以，本文提出一种新的直觉模糊熵公式并给出证明：

E(A)=

(1)

从式(1)可以看出，新的直觉模糊熵公式里包括犹豫度πA(xi)和隶属度与非隶属度的绝对值之差|(uA(xi)-νA(xi))|。下面给出证明：

E(A)=0⟺∀xi∈X

|uA(xi)-νA(xi)|(uA(xi)+νA(xi))=0 ⟹

|uA(xi)-νA(xi)|=0

因为

uA(xi)∈[0,1],νA(xi)∈[0,1]

所以

uA(xi)+νA(xi)≠0⟹uA(xi)=νA(xi) ⟺

∀xi∈X,uA(xi)=νA(xi)

E(A)=1⟺∀xi∈X

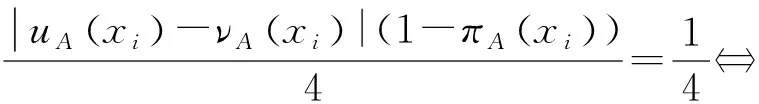
|uA(xi)-νA(xi)|(uA(xi)+νA(xi))=1⟺

因为

uA(xi)∈[0,1],νA(xi)∈[0,1]

所以

uA(xi)=1 ⟺∀xi∈X

〈uA(xi),νA(xi)〉=〈1,0〉,∀xi∈X

|uA(xi)-νA(xi)|∈[0,1]

(1-πA(xi))∈[0,1]

由于直觉模糊熵公式为单调递增函数， 并且由上面的推导可知：

uA(xi)-νA(xi)≥0⟹uA(xi)≥νA(xi)

令uA(xi)≤uB(xi),νA(xi)≥νB(xi),πA(xi)=πB(xi)，有

|uA(xi)-νA(xi)|≤|uB(xi)-νB(xi)| ⟺

E(A)≤E(B)

由此可以得出，E(A)是一个包含犹豫度信息的直觉模糊熵，并且是有效的。

1.3 模糊C均值算法

模糊C均值算法在硬模糊C均值算法的基础上加入了模糊划分矩阵。 FCM算法中用隶属度来表示样本中某个数据对于某个类的归属程度。下面通过数据模型直观表示,如图1、图2所示。

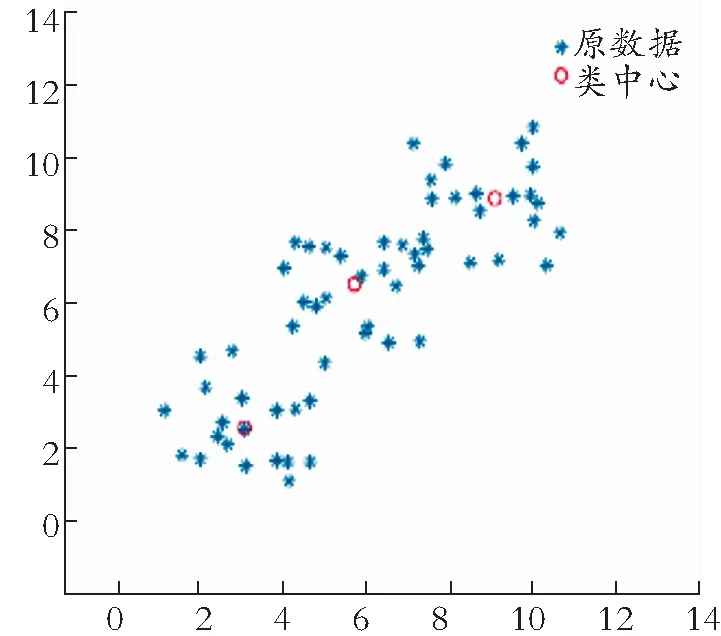
图1 数据聚类散点图Fig.1 Scatterplot of data cluster

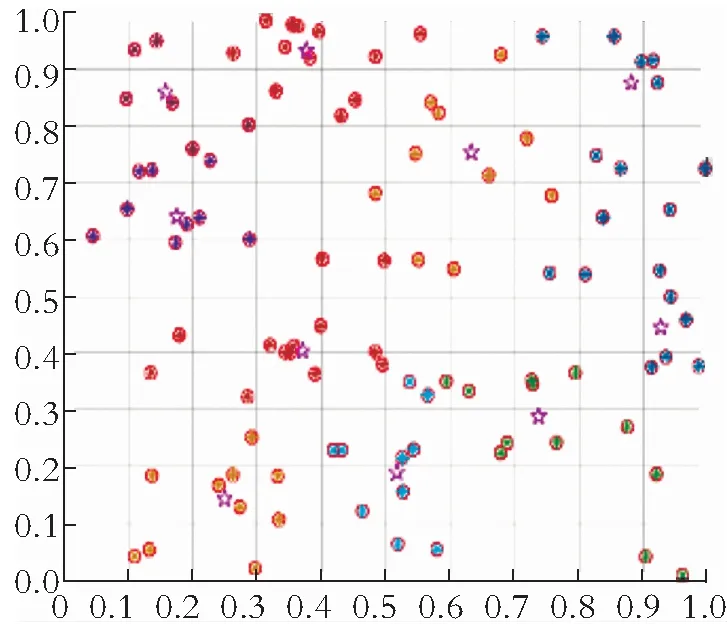
图2 数据在不同聚类中心分布Fig.2 Data distributed in different cluster centers

从图1可以大致看出样本数据归属于哪一个类中心，但是不能清楚直观地看出哪一个数据样本归属于哪一个类中心，但是在图2中可以很清楚地看到每一数据样本都很好地归属于一个类中心。

下面介绍FCM的定义：FCM把xi(i=1,2,…,n)分为c个模糊组，划分的依据为

则FCM的目标函数就是

(2)

这里uik为隶属度，介于0，1之间，vk为模糊组K的聚类中心，dik=||vk-xi||为第k个聚类中心与第i个数据点间的欧几里得距离，m是加权指数，又称平滑参数，且m∈[1,+∞),但是通常取m=2。图3给出了FCM算法的流程图(ε为收敛精度)。

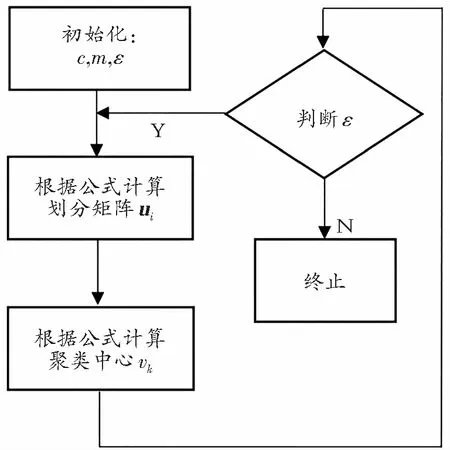
图3 FCM算法流程图Fig.3 Flowchart FCM algorithm

采用拉格朗日乘数法构造新的目标函数,分别对L的u,v,λ求偏导，然后令所求的偏导为0，联立3个式子求解就可以得到隶属度uik和聚类中心vk的表达式。构造函数如下[7]：

(3)

隶属度的值为

i=1,2,…,c;k=1,2,…,n

(4)

聚类中心为

(5)

算法步骤为

① 输入图像，设定聚类类别数、模糊指数，初始化聚类中心，设置迭代停止阈值以及最大迭代次数；

② 更新隶属度；

③ 更新聚类中心；

④ 看是否满足标准化测度函数的条件，若满足，停止算法并输出隶属度和聚类中心，否则循环执行步骤②；

⑤ 根据最大隶属度原则进行图像像素点的划分，实现图像分割[8]。

2 融入新加权因子的直觉模糊C均值算法

2.1 已有的改进模糊C均值算法

文章前面介绍了FCM算法，由于它的原理很符合实际情况，所以应用比较广泛，但是在应用中经常受到噪声干扰，碰到复杂性图像处理效果不理想，鲁棒性较差。所以人们对原有FCM算法进行一系列的改进，接下来着重介绍IFCM和KFCM。

2.1.1 直觉模糊C均值算法IFCM

通过文字表面意思可以看出，IFCM算法就是在FCM算法中融入了直觉模糊隶属度。下面给出目标函数：

(6)

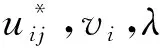
2.1.2 基于核改进的模糊C均值聚类算法KFCM

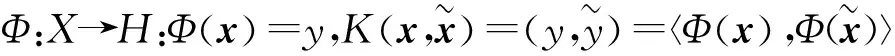
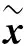
定义目标函数为

其中,K(vi,xj)是高斯径向基函数，其表达式为

(7)

其中,1-K(xj,vi)是像素i到邻域窗内像素k的高斯核函数，用于计算像素点到聚类中心的距离。然后利用拉格朗日乘数法构造新的目标函数L(构造方法参考上述的FCM算法)，对L的λ，uij，vi求偏导，然后令所求的偏导为0，联立3个式子求解可得出：

隶属度值为

(8)

聚类中心为

(9)

KFCM算法提高了聚类性能，但对图像边缘细节部分的处理没能得到解决。KFCM算法对噪声和孤立点的鲁棒性较好，鲁棒性指算法在一定的参数(如噪声)摄动下，对图片处理效果的好坏，可以通过一系列的评价指标来判断算法的鲁棒性。通过文献阅读知道KFCM算法的迭代次数最少，因此运行时间会大大减少。算法步骤可以参考文献[12]。

2.2 改进的直觉模糊C均值算法

2.2.1 抑制式算法

抑制式算法可以在算法运行的时候，突出主要因素，减少从属因素干扰，有效提高算法的处理速率。引入这个概念的原因在于考虑到新算法结合IFCM和KFCM，可能会导致算法运行速度变慢，那样就失去了新算法的意义，所以引入一个抑制式算法改进一下新算法的运行速率。假设样本xj属于第m类，且它对于m这个类的隶属度是最大的，记为umi,则修正后的隶属度为

(10)

其中，α是抑制因子。当α=0的时候，算法变成HCM算法；当α=1的时候，算法变成FCM算法。α的取值决定图像分割的效果和算法的收敛效果，由于α只能在0到1取值，所以折中考虑，取α=0.5。因为新的直觉模糊集生成方法中犹豫度和抑制因子取值范围相同，所以采用像素点的隶属度求出犹豫度作为抑制因子的值去修正像素点的隶属度，不同的样本点产生不同的抑制因子，所以α的计算方法[13]为

αij=πij=2uij(1-uij)

(11)

2.2.2 KWIFCM算法

由于IFCM算法没有包含空间信息，所以本文提出了一种基于IFCM和KFCM改进的新算法：KWIFCM算法。该算法重新定义了加权模糊因子，该模糊因子包含了空间信息，并且引入高斯核距离代替欧几里得距离计算像素点之间的距离，提高了算法对加噪图像的分割精度。在新算法中，需要对核空间和直觉模糊集对模糊C均值修正的目标函数和直觉模糊熵两个函数求最小值，修正的目标函数为式(12)，初始聚类中心的选取依靠式(1)。这样可以使算法不易陷入局部最优，增强算法性能，具体可以参考文献[14]和式(17)。由于新算法中包含隶属度、非隶属度、犹豫度和新的模糊因子，所以JKWIFCM=Jω+Jπ，下面给出新算法的目标函数：

(12)

其中，

(13)

(14)

K(x,y)=〈φ(x),φ(y)〉=φ(x)Tφ(y)

(15)

(16)

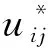
(17)

其中，Exk是特征xk的直觉模糊熵，见式(1)。数据样本的特征权重反映了评价指标对能否实现这次评价的相对重要程度，但是不能保证样本分布是均匀分布的，一定是杂乱无章的，所以要采用特征加权方法对样本进行加权，从而挑选出权重比较大的部分，在这个区域当中选取初始聚类中心，然后利用拉格朗日乘数法求出隶属度。

与传统FCM一样，KWIFCM通过不断更新隶属函数和聚类中心来优化目标函数。由于新的加权模糊因子中已经包含像素空间信息，所以新算法不需要引入任何参数，即不需要人为干预，这就要提高算法的准确性。具体算法步骤如下：

① 输入图像、高斯核函数K、聚类数目c、迭代停止阈值δ、加权指数m，根据式(12)(13)(14)计算像素的局部信息；

② 根据直觉模糊熵选取初始化聚类中心；

③ 为高斯核函数修正θ；

④ 根据生成的犹豫度修正隶属度矩阵，判断迭代停止条件：当前的隶属度与前一个隶属度的差值是否小于ε，当条件不满足则重复步骤④，否则停止迭代，输出隶属度矩阵和θ[15]。

2.2.3 算法验证

衡量一个算法的好坏不能仅依靠主观推测和感觉，要通过实验结果验证，所以在评价指标上，引入正确分割率RSA这一概念来评价算法的优越性。定义RSA为

(18)

本文的实验平台是MATLAB 2018b，使用的图像为pen灰度图像、pepper灰度图像和lena灰度图像，且3种图像均为标准灰度图像，灰度值为256×256。pen灰度图像和pepper灰度图像可以代表现实生活中简单和复杂的物体，pen灰度图像细节较少，pepper灰度图像细节较多；lena灰度图像代表人物。对这3幅图像进行分割处理，具有典型的意义。为了验证新算法对噪声图像的分割效果，给图片加的噪声都为均值为0，强度为0.2的高斯噪声。在实验开始前，要交代一些参数的设定：m=2，ε=0.000 001，最大迭代次数为1 000，图4聚类数目c=2，图5聚类数目c=3，图6聚类数目c=4。由于本文使用的计算机处理器为英特尔六代，所以算法在运行时间上会跟其他文献上有所出入。

图4可以看出：pen的灰度图像进行FCM算法处理后，图片显示出一些细节部分，灰度对比很明显。FCM算法处理的pen灰度图像背景较暗，经过本文算法处理后，背景基本上为一片黑色，说明此时的灰度值较大，经过测量计算可知此时背景的灰度值已达到251，这样更能突出所分割图片的有效信息。加入高斯噪声的图片经过两种算法处理后得到的效果跟上述结果大相径庭。

(a) pen灰度图

(b) FCM算法

(c) KWIFCM算法

(d) pen加噪图

(e) FCM算法

(f) KWIFCM算法图4 pen图像分割效果对比图Fig.4 Comparison of pen image split effect

从图片中也可以看到新算法对加噪图片的抗噪性也是比较优秀的。以lena灰度图片和lena加噪图像为例(图5)，原灰度图像经FCM算法处理后，虽然图片像素明暗一目了然，但噪声也可以看得很清楚，经本文提出的算法处理后，背景灰度明显变暗，此时灰度值达到247，人物信息被很好凸显；FCM对lena加噪图片的处理并不是很理想，处理过后的图片背景明暗交替分布，这为算法处理不掉的噪声区域，但是进行KWIFCM算法处理后，明暗交替部分已经明显减少，可知噪声区域在减少。从图6可以看到：pepper原图像和pepper加噪图进行KWIFCM算法处理后，效果明显优于FCM，噪声区域明显减少或消失，新算法对细节的分割效果也很有效。可以得出结论：新算法的稳定性较高，不管对于简单图像还是复杂图像，处理结果都能达到人们想要的效果。

(a) lena灰度图

(b) FCM算法

(c) KWIFCM算法

(d) lena加噪图

(e) FCM算法

(f) KWIFCM算法图5 lena图像分割效果图Fig.5 Comparison of lena image split effect

(a) pepper灰度图

(b) FCM算法

(c) KWIFCM算法

(d) pepper加噪图

(e) FCM算法

(f) KWIFCM算法图6 pepper图像分割效果对比图Fig.6 Comparison of pepper image segmentation effect

为了防止实验数据出现偶然性，所以做了10次随机实验并对实验数据进行了平均化处理(表1、表2)。

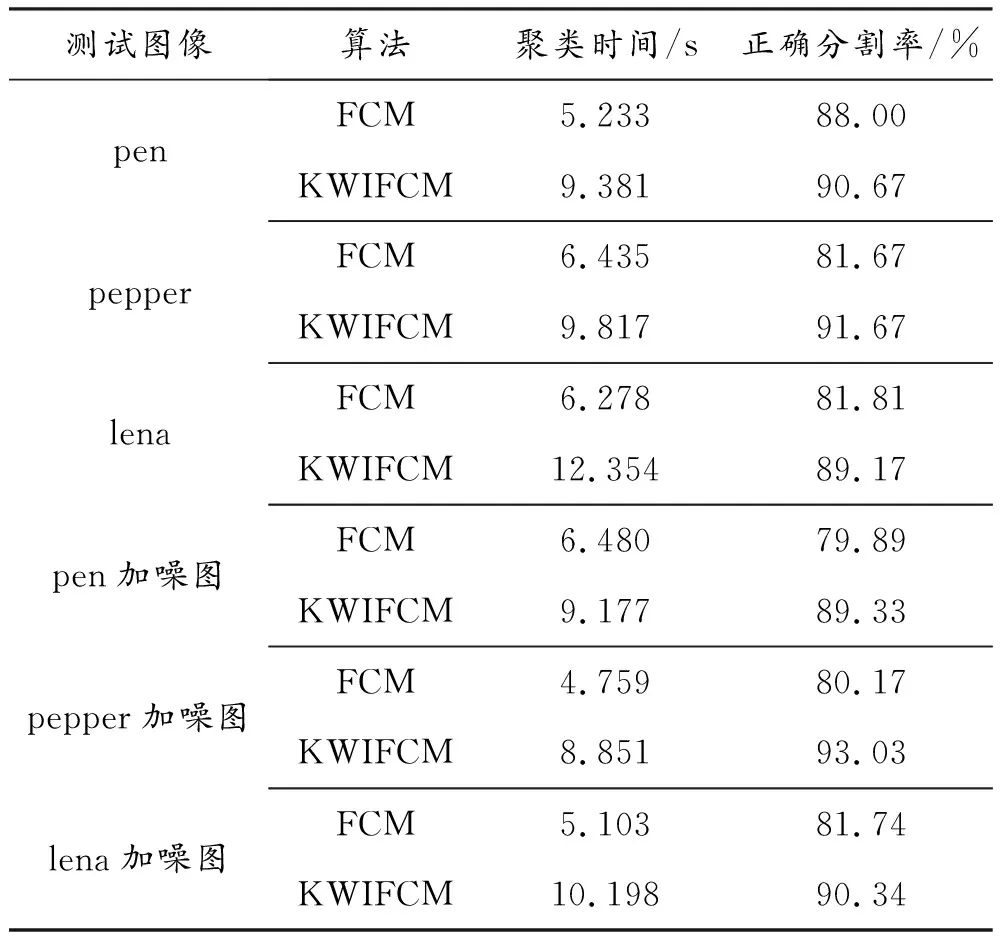
表1 两种算法对图像分割效果的对比Table 1 Comparison of the image segmentation effects of two algorithms

表2 两种算法迭代次数对比Table 2 Comparison of the number of iterations of two algorithms

从表1实验数据可以看出：只有pen灰度图像在FCM算法和KWIFCM算法分别处理后的正确分割率相差不多，而其他灰度图像分别进行FCM算法和KWIFCM算法处理后，其正确分割率差值在10%左右。可能的原因在于pen灰度图像细节不多，而其他图像细节比较多。新算法的聚类时间虽然比FCM算法要多出大概一倍的时间，但其处理效果明显优于FCM算法。

从表2可以看出改进算法的迭代次数有所减少。综合来说，改进的算法是一次成功并且有效的改进。

3 已有改进FCM算法的实际应用

已有改进的FCM算法不在少数，所以本文只对IFCM，KFCM和本文新提出的算法进行介绍。在实际应用中，评价分割好坏的指标除了正确分割率之外，还有本节引入的4项指标。灰度均值代表像素点的平均值，像素点越大，代表图像分割越精确，即灰度均值越大，图像的分割精度越高。标准差用于反映数据的波动性，标准差越大，则图像的黑白像素点分明，分割的图像也越清晰。熵反映混乱度，是一种能量的概念，熵越大，则表明图像的信息越多，分割的结果也就越准确。平均梯度即灰度的变化率大小，平均梯度越大，则图像越清晰。

由于上文已经对高斯噪声进行处理，所以不再进行赘述，本节对图像添加椒盐噪声进行处理和分析。初始参数的设定和上文一样，椒盐噪声的强度设定为0.1。选取的图片为pepper和lena灰度图像(图7，图8)。

(a) pepper灰度图

(b) pepper加噪图

(c) FCM算法

(d) IFCM算法

(e) KFCM算法

(f) KWIFCM算法图7 强度0.1椒盐噪声下pepper分割对比图Fig.7 Comparison of segmentation of pepper images when the intensity of impulse noise is 0.1

(a) lena灰度图

(b) lena加噪图

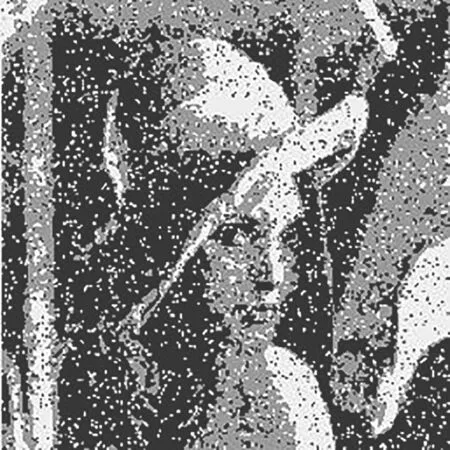
(c) FCM算法

(d) IFCM算法

(e) KFCM算法

(f) KWIFCM算法图8 强度0.1椒盐噪声下lena分割对比图Fig.8 Comparison of segmentation of lena images when the intensity of impulse noise is 0.1

从上面的实验结果可以看出:FCM算法抗噪能力依然不强，处理后的图片中仍包含一些椒盐噪声点；IFCM算法虽然有处理不确定信息的能力，但对椒盐噪声几乎没有抑制作用，处理后的图片噪声基本没有得到遏制；KFCM算法包含了空间信息，有效减缓了椒盐噪声的干扰，对椒盐噪声鲁棒性一般，而且对图片一些不确定信息的处理不很理想；KWIFCM算法包含了空间信息的模糊因子、加快算法运行效率的抑制因子和处理不确定信息能力的直觉模糊C均值算法，从结果可以看出：KWIFCM算法对图片的分割效果优于其他算法，并且对椒盐噪声鲁棒性较好。

表3即为4种算法在椒盐噪声下的分割效果对比图。

表3 4种算法在椒盐噪声下的分割效果对比(10次随机实验)Table 3 Comparison of the split effect of four algorithms under impulse noise (10 randomized experiments)

从表3可以看出：4种算法的聚类时间有所不同。由于KWIFCM算法在迭代过程中引入核函数和每次迭代都要计算的加权模糊因子，因此其聚类时间有所延长，并且KWIFCM算法加入了抑制因子，增加了聚类时间，但并不影响KWIFCM算法分割的正确率。并且从上文可知，KWIFCM算法对高斯噪声的鲁棒性也是最佳的。综上， KWIFCM算法在图像分割时，对高斯噪声和椒盐噪声有着明显的抑制效果。

从表4、表5当中的数据可以看到:在pepper加噪图中经KWIFCM算法处理后的图像灰度均值、标准差和平均梯度最大，而熵值却最小。在lena加噪图中，经KWIFCM处理后的图像标准差和平均梯度最大，而熵值同样为最小。让人意外的是，经FCM处理后的图像灰度均值居然最大，可能的原因是FCM算法对椒盐噪声处理效果不佳导致噪声点对灰度均值的计算产生了干扰；而熵值都为最小，可能是因为处理后的图片只有黑白两种像素点，虽然能够直观地看出分割效果，但会有一些非常细微的信息在处理时丢失，而其他算法熵值之所以高，可能是因为对噪声对处理结果的影响。总体来说，改进算法对噪声图像分割有着明显的优势。

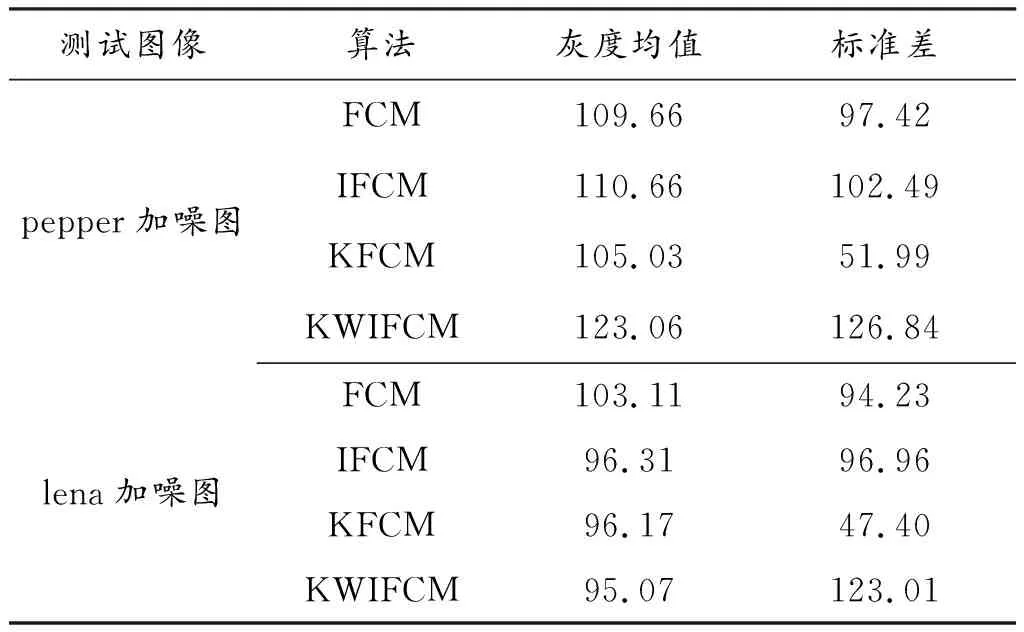
表4 4种算法对椒盐噪声图像分割时的灰度均值、标准差、熵、平均梯度Table 4 The mean grayness, standard deviation, entropy and average gradient when using four algorithms to split images under impluse noise

表5 4种算法对椒盐噪声图像分割时的熵、平均梯度Table 5 Entropy and average gradient when using four algorithms to split images under impulse noise

4 总结与展望

本文提出的改进算法减少了算法时间，同时实现了多种功能。在IFCM算法和KFCM算法的基础上进行了改进，除了引入直接模糊集和高斯核距离，还在目标函数中加入了加权模糊因子，目的是为了引入像素的空间信息；利用直觉模糊熵公式选取初始聚类中心，可以防止算法陷入局部最优；在算法中加入抑制因子，目的是为了减少运行时间。

未来对图像分割的要求会越来越严格，针对提出的算法给出建议：第一，算法的运行时间较长，可能是抑制因子α的选择没有做对比实验，没有选出最佳的α值，导致实验结果不理想。第二，图像分割正确率提高不明显，只能停留在90%左右，没有达到令人满意的效果。可以将直觉模糊集推广到中智集来提高算法的处理能力，更多了解可以参考文献[16]。