高导无氧铜等温压缩系数推算模型研究

刘文静，张海洋，高 波*，罗二仓，Laurent Pitre

（1.中国科学院理化技术研究所 中法低温计量科学与技术国际联合实验室，北京 100190；2.中国科学院理化技术研究所 中国科学院低温工程学重点实验室，北京 100190；3.中国科学院大学，北京 100049；4.法国国家计量院，法国 巴黎 F93210）

0 引言

低于24.556 1 K（氖三相点温度）的深低温区热力学温度的高准确度测量，对前沿科学研究和大科学装置运行具有重要意义。热力学温度的基准级（测温准确度＜1 mK）测量是深低温区高准确测温技术的基石。

当前，用于深低温区基准级热力学温度测量的方法主要有定容气体法[1]、介电常数法[2]、声学法[3]和气体折射率法[4-5]。其中，声学法和气体折射率法均采用微波谐振法进行测量，实验中均需使用与高导无氧铜近似的电解质铜（Cu-ETP）制成的微波谐振腔体在真空和充气状态下分别进行测量。该种材料热导率高，低温下性能稳定，便于进行控温；导电率高，趋肤效应小，可提高谐振频率测量准确度。电解质铜制成的微波谐振腔为空心腔体，当谐振腔充入气体承受高压时，谐振腔体会发生变形并影响最终热力学温度测量，腔体变形量用等温压缩系数表示。由最新气体折射率测温结果[5]发现，等温压缩系数对测量的热力学温度贡献了最大的不确定度分量。为提高测量准确度，需要对腔体变形产生的影响进行修正，即需要得到高准确度的腔体材料等温压缩系数。由于缺乏电解质铜文献数据，本文采用高导无氧铜数据建立模型，并与文献模型比较，可应用于研究电解质铜的等温压缩系数。

目前，确定高导无氧铜等温压缩系数的方法有实验测量和理论推算两种。实验测量方面，按照所测量的物理量分为两种：一种是直接法，利用激光干涉仪[6]测量材料在同一温度下不同压力和方向上的形变，从而获得等温压缩系数kT；另一种是间接法，利用超声多普勒测振仪[7-8]、微波干涉仪[9]、密度仪和绝热量热仪[10]分别测量材料的绝热压缩系数ks、体积膨胀系数αV、密度ρ和比热cp，结合关系式kT=ks+αV2T（/ρcp）间接计算kT。理论推算方面，2016年，Gaiser等[11]基于Grüneisen[12]和Anderson[13]的 工作 提出了等温压缩系数推算模型，并应用于高导无氧铜等温压缩系数的推算，但推算偏差较大，尤其是在深低温区。为满足该温区高导无氧铜等温压缩系数计算准确度的要求，本文建立拟合结果好、形式简洁、适用于深低温区的高导无氧铜等温压缩系数推算模型，以应用于等温压缩系数的推算。

1 等温压缩系数推算模型

等温压缩系数是材料的热物性参数之一，表示当物体温度一定时，压力每升高1 Pa时的体积变形量。当谐振腔充入气体承受高压时，腔体会发生变形，影响相关物理量测量。而深低温环境较难获得，相应深低温区实验数据较少，通常基于室温数据借助推算模型获得。德国联邦物理技术研究院开展了高导无氧铜等温压缩系数的模型推算研究[11-12]，所提出的模型存在深低温区推算偏差大、形式较复杂的问题，需要发展更好的高导无氧铜等温压缩系数推算模型。

1.1 高导无氧铜物性数据

本文所采用的高导无氧铜等温压缩系数“实验数据”通过式（1）获得：

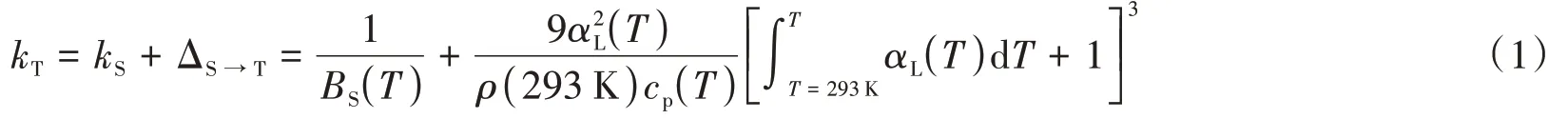
式中：kS为绝热压缩系数[14-15]；BS为体积模量[14-15]；αL为线膨胀系数[16]；cp为定压比热[17-18]；密度ρ[19]均为文献实验数据。

1.2 目标函数

本文中所有数据分析均采用以下目标函数f来表述，如式（2），即采用文献实验值与模型拟合值相对偏差的加和来计算：

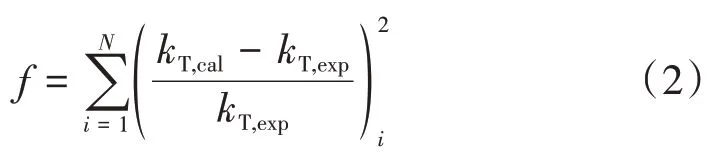
式中：i为实验数据序列号；N为实验数据点数；下标“exp”和“cal”分别表示高导无氧铜等温压缩系数的实验值和拟合值。

1.3 评价指标

本文采用的评价指标主要有：相对偏差δRD（Relative Deviation，RD），平均绝对相对偏差δAARD（Average Absolute Relative Deviation，AARD）、最大绝对相对偏差δMARD（Maximum Absolute Relative Deviation，MARD），其计算式分别为式（3）～（5）：

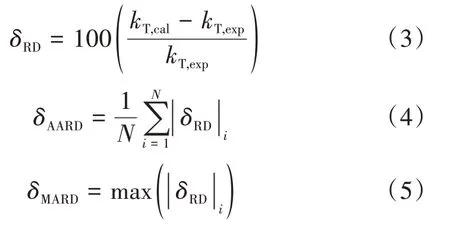
式中：max表示取最大值。

1.4 文献模型

Gaiser等[11]针对高导无氧铜的等温压缩系数的计算提出推算模型，如式（6）：

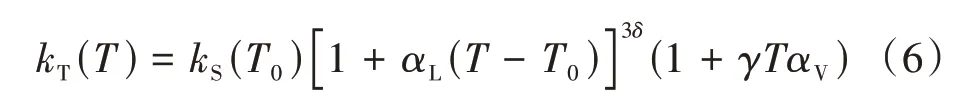
式中：T、T0（273.16 K）分别为等温压缩系数计算温度和参考温度；αL为线膨胀系数（αV=3αL）；δ、γ分别为Anderson-Grüneisen和Grüneisen参 数，其 计 算式[7-8]分别为式（7）（8）：

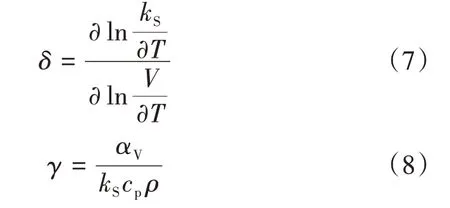
δ、γ取其室温附近值的平均值，为更好地比对，本文将δ、γ作为待定参数用于等温压缩系数的推算。

1.5 本文模型

针对Gaiser提出的模型推算偏差相对较大的情况，本文在该模型基础上提出优化推算模型，如式（9）：

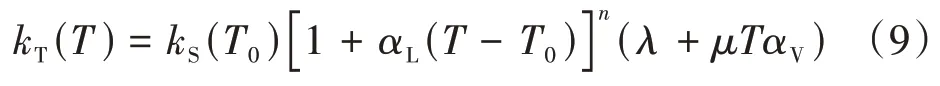
式中：n、λ和μ为待定参数，由实验数据拟合确定。

为了确定式（9）中参数n的大小，采用Levenberg-Marquardt算法[20]和式（1）对0～300 K高导无氧铜等温压缩系数的实验数据进行拟合。拟合结果如图1所示，拟合结果如表1所列，可以看出，优化推算模型能很好地关联实验数据，相对偏差在0.10%以内。

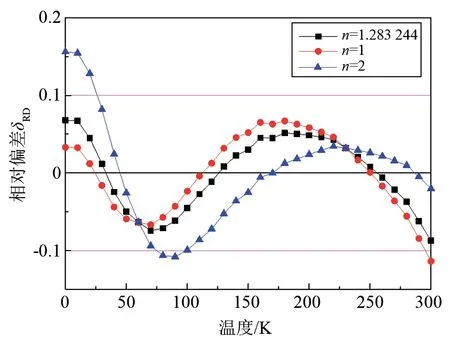
图1 高导无氧铜等温压缩系数的拟合结果Fig.1 Fitting results of isothermal compression coefficient of high conductivity oxygen free copper

但如式（9）所示的三参数方程在由部分数据拟合后外推时会出现不合理结果（例如数据点少、未知量多时，会存在过拟合现象，拟合结果可能为不合理的复数），为提高方程拟合效果，同时考虑到方程的简洁性，本文将参数n设为1或2。设定n后拟合结果如表1和图1，可以看出，n=1时拟合结果与最优结果（n=1.283 244，如图1中黑色线所示）更接近，大部分数据相对偏差均在0.10%以内，并且此时方程为简洁的一次函数形式，因此，式（9）设n=1，转换为式（10）。

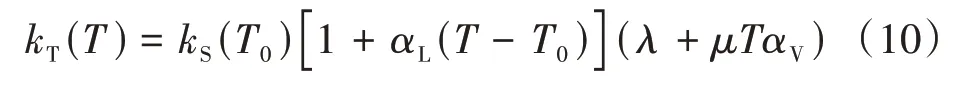
表1 0～300 K实验数据拟合结果Tab.1 Fitting results of experimental data from 0 to 300 K

2 计算结果及分析

本文首先通过拟合有限的数据获得式（9）的待定参数λ和μ以及和式（6）的待定参数δ和γ，将所建模型外推至其他温区并与实验数据进行对比以检验模型的外推预测能力。为更好地考察本文模型和文献模型的外推能力，将待分析数据分为三个温区：室温区（260～280 K，采用空调制冷，容易获得）、低温区（140～160 K，采用混合工质制冷，较易获得）和深低温区（10～30 K，采用脉冲管等方法制冷，较难获得）。拟合和外推预测结果如表2所列，图2～5分别给出了不同温区本文模型与文献模型的计算结果。

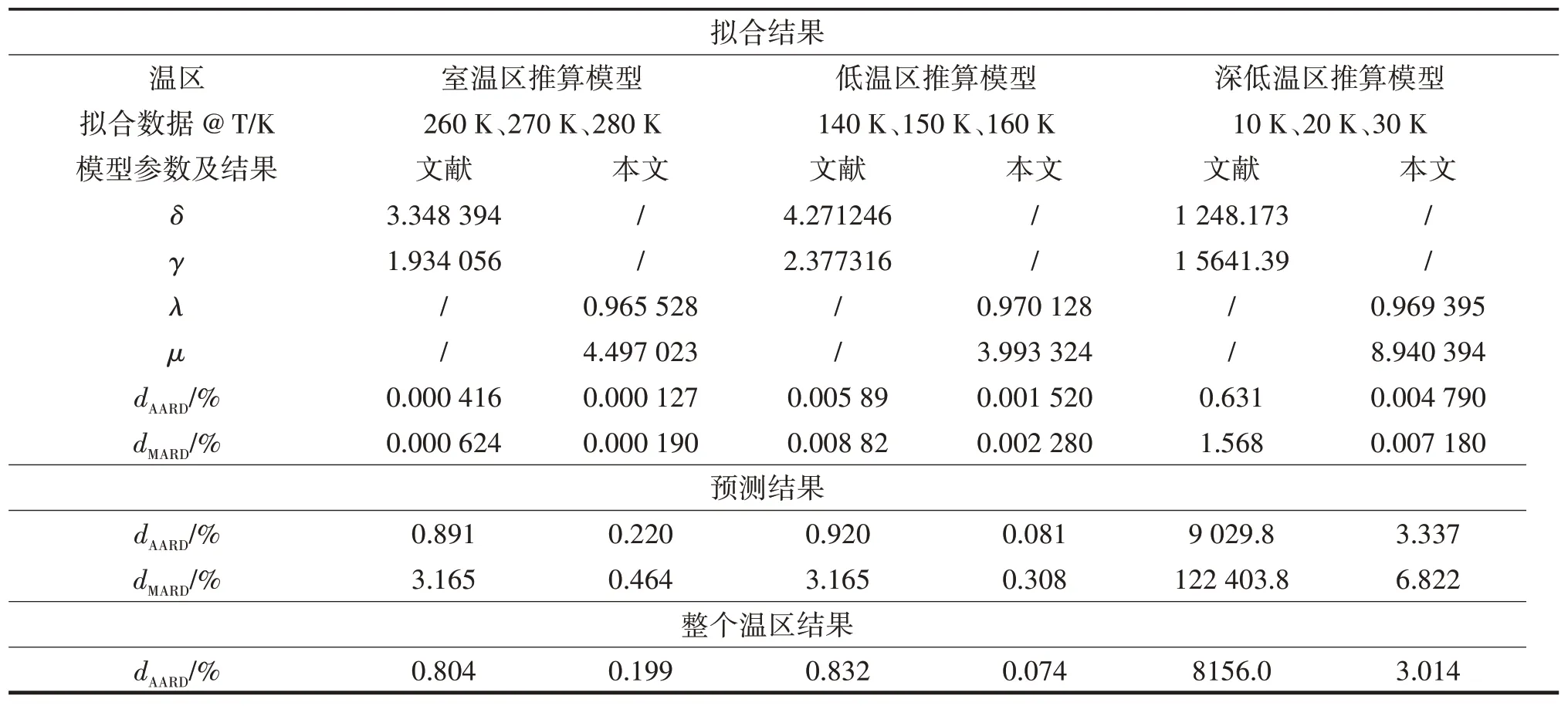
表2 不同温区拟合及其预测结果Tab.2 Fitting and prediction results of experimental data of different temperature zone

由图2（a）可以看出，在室温区，随着目标温度远离拟合温度区间，两个模型的预测相对偏差呈增大趋势。从整体温区拟合结果可以看出，本文模型预测相对偏差均在0.50%以内，明显高于文献模型预测结果（δAARD为0.891%），尤其是在0～100 K温区。由图2和3可以看出，低温区、深低温区与室温区的预测结果相似，随着目标温度远离拟合温度区间，两个模型预测相对偏差呈增大趋势，整体而言，本文模型预测结果均明显优于文献模型预测结果。室温区、低温区和深低温区本文模型预测结果的δAARD分别为0.220%、0.081%和3.337%，将所有数据按式（4）计算 可 得 整 体δAARD，3个 模 型δAARD分 别 为0.199%、0.074%和3.014%，低温区模型推算结果最好。

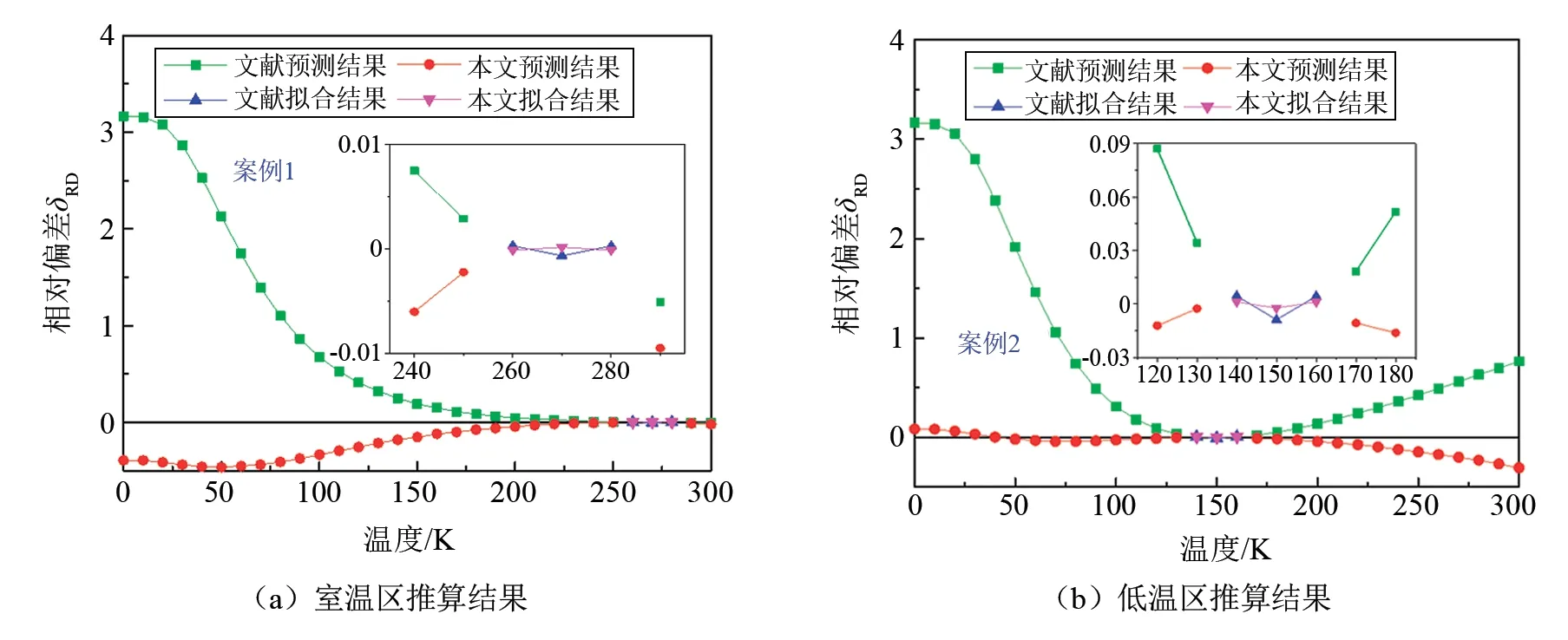
图2 室温区和低温区文献模型和本文模型等温压缩系数推算结果Fig.2 Extrapolation results of isothermal compressibility of model from literature and this work

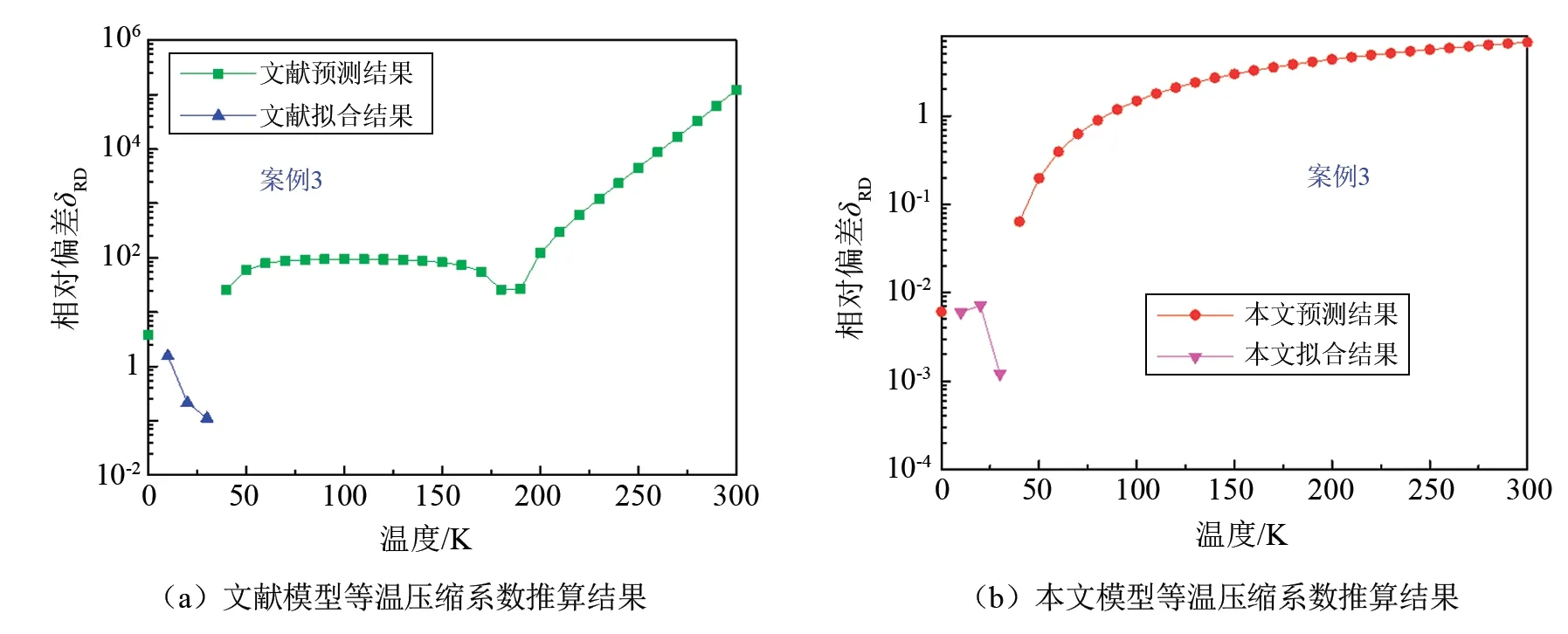
图3 深低温区文献模型和本文模型等温压缩系数推算结果Fig.3 Extrapolation results of isothermal compressibility of model from literature and this work at ultra-low temperature

图4给出了文献模型中δ、γ随拟合温区平均温 度的变化趋势，可以看出，大于200 K时δ、γ值的大小随温度变化较小，小于150 K时δ、γ值的大小随温度变化开始迅速上升，在深低温区达到最大值，正是由于δ、γ值的大小随温度变化剧烈使得由拟合进行外推时的结果很差。

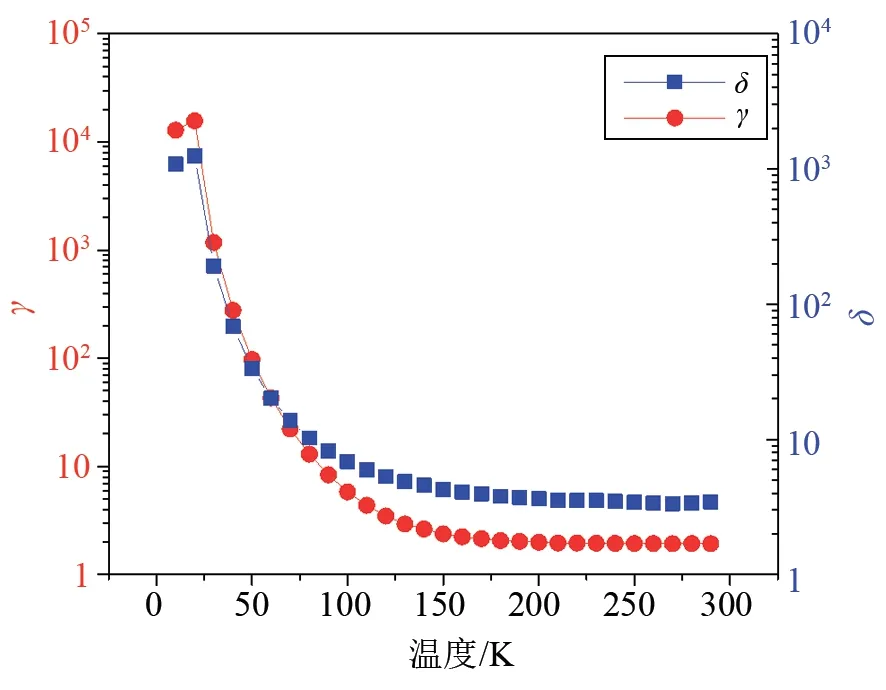
图4 文献模型拟合参数δ、γ值随温度的变化Fig.4 Variation of fitting parametersδandγof literature model with temperature

图5给出了本文模型中λ、μ随拟合温区平均温度的变化趋势，可以看出：在0～300 K温度区间λ值波动变化很小，为0.969±0.002（1倍标准差）。μ值在50～300 K温度区间变化较小，为4.20±0.25（1倍标准差）；小于50 K时随着温度的降低，μ值迅速增大，但是该温区内μ值的绝对值仍然比文献中的γ值小3个数量级。因此，本文模型在整个温度区间的外推计算结果均优于文献模型。

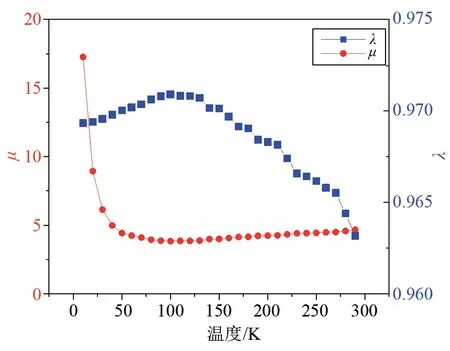
图5 本文模型拟合参数λ、μ值随温度的变化Fig.5 Variation of fitting parametersλandμof model in this work with temperature

利用本文深低温区推算模型对5～25 K温度区间高导无氧铜等温压缩系数进行了推算，结果如图6，其中，实验数据来自美国国家标准与技术研究院（NIST）数据库[10]。由图6可以看出，计算相对偏差均在0.06%以内，δAARD为0.048%，可满足该温区对高导无氧铜等温压缩系数计算准确度的要求。接下来可将该模型进一步应用到电解质铜、316不锈钢等材质的等温压缩系数推算研究中，以检查本文模型的普适性。

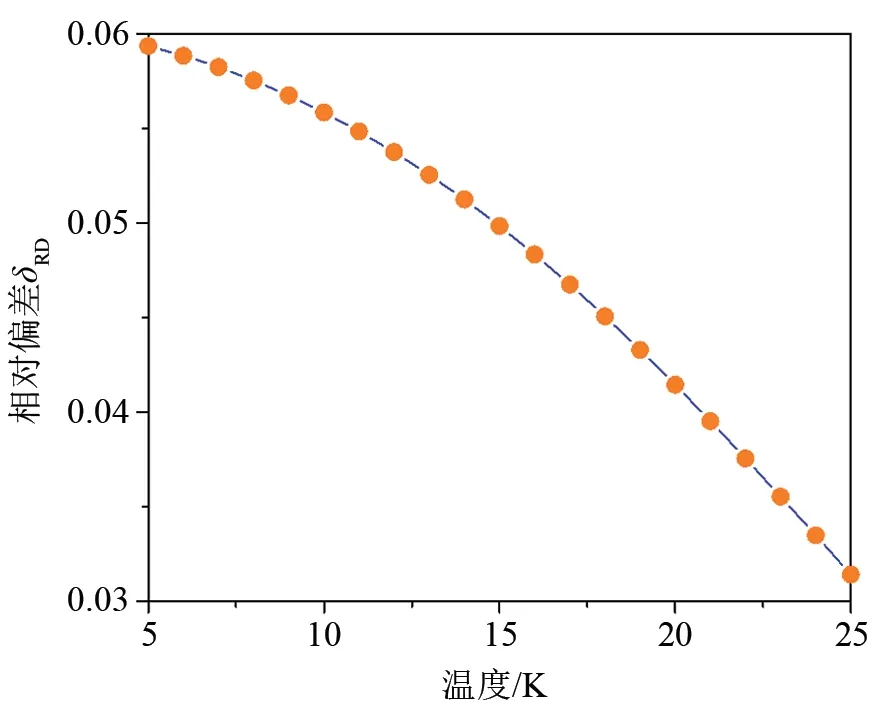
图6 本文低温区模型推算5～25 K高导无氧铜等温压缩系数相对偏差Fig.6 Relative deviation of isothermal compressibility of oxygen-free high conductivity copper calculated by model from 5 to 25 K

3 结论

本文建立了高导无氧铜的等温压缩系数推算模型，适用温度范围为5～300 K。该模型推算结果优于文献模型推算结果，主要是因为该模型中两个拟合参数与文献模型中的参数相比，随温度变化的剧烈程度较小；分别在室温区、低温区和深低温区进行推算研究，结果显示该模型在低温区推算结果最好，5～25 K温区高导无氧铜等温压缩系数的推算相对偏差在0.060%以内，可满足该温区对高导无氧铜等温压缩系数计算准确度的要求，进而通过气体折射率法实现热力学温度的高准确度测量。未来可将本文模型应用到电解质铜、316不锈钢等材料的等温压缩系数推算研究中，以检查模型的普适性。