质子交换炉温控系统的模糊解耦预测控制

伏 娜，张 晞

(北京航空航天大学仪器科学与光电工程学院，北京 100191)

0 引言

铌酸锂(LiNbO3)晶体具有优异的电光和声光等特性，被广泛用于制备各种光波导器件[1-2]。铌酸锂光波导是高精度光纤陀螺的核心器件，质子交换炉是用质子交换法制备铌酸锂光波导的主要设备，炉温的波动直接影响波导深度的变化，导致光波导性能不稳定，同时对不同批次制备的光波导的一致性也有较大影响，因此实现炉内温度的精确控制非常重要。一般用于制备半导体器件的加热炉采用整段加热控温，其温度场分布均匀性差。为了满足生产工艺的要求，提高生产效率，质子交换炉一般采用大哥三段控温的方式以提高炉内温度分布均匀性，但这同时引入了温度耦合的问题。质子交换炉是一个具有非线性、强耦合、多变量、大滞后、多干扰特点的复杂对象，目前国内质子交换炉的温度控制一般采用3路PID控制，由于控制算法本身的限制，在质子交换炉温度控制上存在许多不足，如PID控制参数不能自动调节、不具有自适应性、调节不及时等问题，且炉内3段温度相互耦合，单靠传统的PID控制无法消除回路之间的耦合，故控制效果不理想，很难满足控制精度的要求[3-5]。

质子交换炉是一个具有非线性、强耦合、多变量特点的系统，针对系统回路之间的耦合，采用模糊解耦控制方法是降低系统耦合程度的一种有效办法[6-8]。但是，随着我国铌酸锂光波导制备技术的不断发展，质子交换炉的温度稳定性要求越来越高，单纯采用模糊解耦控制只能降低扰动对另一回路温度输出的影响，并不能减弱干扰对自身回路造成的温度波动，因此并不能取得良好的控制效果。而模型预测控制(model predictive control，MPC)算法作为一种先进控制方法，在具有大滞后、多干扰特点的场合下，基于鲁棒性强、控制效果好的优势在许多工业过程上得到了应用[9-13]。本文为解决炉温控制问题，基于热平衡机理推导出了质子交换炉简化机理模型，基于模型提出了模糊解耦与预测控制相结合的控制方法，组成在机理上互补的集成控制策略，以降低系统耦合并提高系统抗干扰能力，最后通过仿真验证了所提策略的可行性与有效性。

1 控制对象及建模

1.1 控制系统介绍

控制对象是质子交换炉，采用圆筒结构，立式放置，炉体结构由外至内分别有保温层、加热丝、炉管。炉管由石英材料制成，在炉管上均匀缠绕了3段电阻加热丝，可以分别独立供电。在每组加热丝的中间有一副用于测量温度的热电偶。炉管外部的保温层由绝热材料制作而成。工作时，通过控制3段炉丝的加热功率，使炉膛内的温度稳定在目标温度值。

3段控温质子交换炉温度控制系统原理图如图1所示。热电偶输出的模拟信号经过A/D转换后成为温度数字信号，该信号经单片机处理后由定时器产生脉宽调制信号，逻辑阵列GAL将脉宽调制信号分为3路分别送到3个MOS管上，由此分别控制各组加热丝的加热功率，从而实现温度控制。

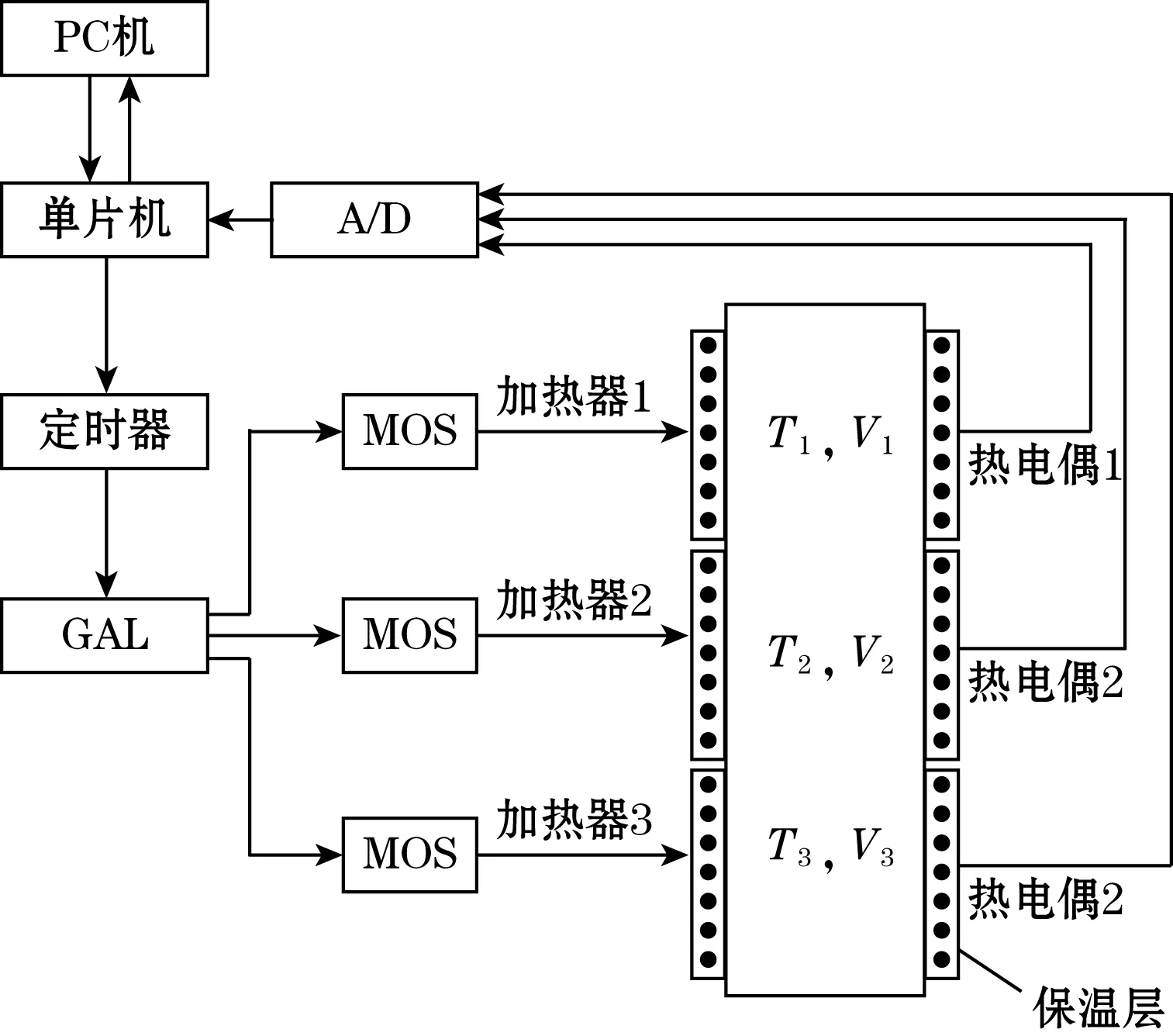
图1 质子交换炉温控系统原理图

1.2 质子交换炉温控模型的建立

质子交换炉在3段控温下，炉膛内空气温度分布分别对应第一温区、第二温区和第三温区。Ti、Vi、Ki、UiIi(i=1,2,3)分别为第i温区的温度、体积、输入占空比、输入功率。ρ为空气的密度，c为空气的比热容。根据能量守恒定律，可得

第一温区空气的热量传递微分方程为

(1)

第二温区空气的热量传递微分方程为

(2)

第三温区空气的热量传递微分方程为

(3)

(4)

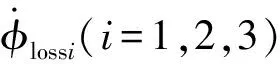
(5)

式中：Tw为炉管外壁温度；Tn为炉管内壁温度；R1为炉管的导热热阻;Tbw为保温层外部的温度；T∞为外界环境的温度；A1为各温区保温层外表面面积；hw为表面传热系数；R2为保温层的导热热阻。

(6)

式中：A2为温区空气截面积；h1-top为第一温区与炉顶的对流换热系数；λ为空气的导热系数；H1为第一温区中心距离炉顶的高度，Ttop为炉顶温度。

(7)

式中：h3-bottom为第三温区与炉底的对流换热系数；H3为第三温区中心距离炉底的高度；Tbottom为炉底温度。

(8)

(9)

式中：h2-1、h2-3分别为第二温区与第一温区、第三温区的空气对流换热系数。

3个温区均选取加热器的控制脉冲作为模型的输入量，U=[N1，N2，N3]T，N1，N2，N3分别表示3个温区加热器的控制脉冲值，3个温区的状态量为每个温区的实际温度X=[T1，T2，T3]T，输出量为各温区的实际温度Y=[T1，T2，T3]T，因此，可将质子交换炉各温区动态模型统一为一种形式，即：

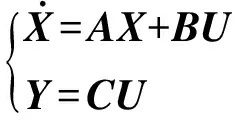
(10)

式中A、B、C为系数矩阵。

经过计算以及试验，质子交换炉的控温目标为240 ℃时，炉膛顶部和底部的温度分别为Ttop=160 ℃，Tbottom=216 ℃，根据传热学中对流换热系数相关计算[14]，可得出：h1-top=2.39 W/(m2·K)，h3-bottom=1.55 W/(m2·K)，h2-1=1.33 W/ (m2·K)，h2-3=0.81 W/ (m2·K)，hw=3.0 W/ (m2·K)。经计算得出系数矩阵分别为：

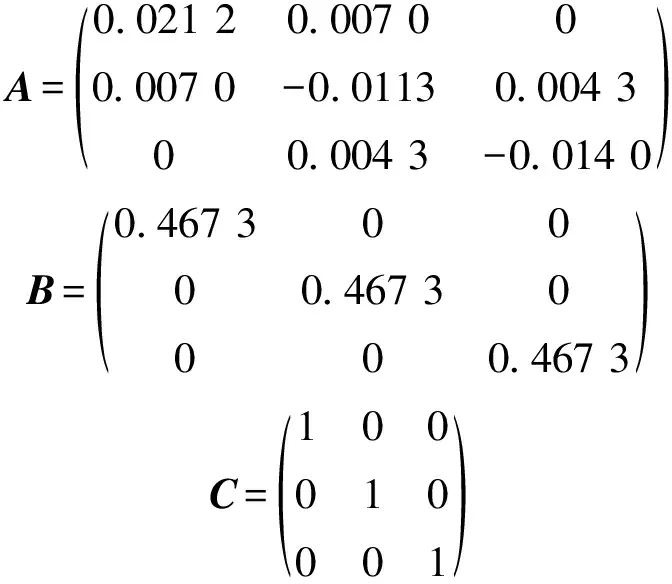
利用MATLAB可以实现状态空间模型到传递函数模型的转换。

1.3 系统耦合性分析

多变量耦合控制系统中，输入、输出变量间的耦合程度可以用相对增益来描述[15]。针对所建立的数学模型，由传递函数矩阵，利用MATLAB编程可求得静态相对增益矩阵：

输入Xj对输出Yi的相对增益λij的大小反映了通道之间的耦合程度[15]。由静态相对增益矩阵可看出，主对角线上的元素都不为1，其值在 (1.1，1.5)区间中，表明系统存在耦合；其中第三温区对应的相对增益为1.169 6，理论上可以不进行解耦也能达到一定的效果；解耦设计重点在第一和第二温区，其受其他操作量的影响最大，这点与工程实际运行情况吻合。因此本文主要对第一和第二温区设计了模糊解耦与预测控制相结合的控制算法。

2 模糊解耦与预测控制相结合的算法设计

图2给出了质子交换炉的模糊解耦与预测控制相结合的设计框图。其中w1、w2分别为第一温区、第二温区的设定值；v1(k)、v2(k)为外部不可测干扰量；y1(k)、y2(k)分别为第一温区、第二温区的输出值；Gm1、Gm2分别为第一温区、第二温区的预测模型传递函数。模糊解耦控制器将多变量系统控制转化为2个单变量系统的控制，实现系统解耦，并对解耦后的系统采用闭环预测控制。

k时刻系统的输出可表示为

(11)

输入为

(12)

下面分别介绍模糊解耦控制器和预测控制器的设计。

2.1 模糊解耦控制器的设计

常规解耦控制方法依赖于系统精确的数学模型，而被控对象的数学模型往往是在一定的假设条件下成立的，所建立的模型不可能完全精确，这种方法具有一定的局限性。模糊控制算法摆脱了数学模型的束缚，开辟了解耦控制的一条新路径。因此，本文在模糊策略的基础上设计了一种模糊解耦控制器，如图2中虚线框内所示。

模糊解耦补偿器1将第二温区控制量u2对第一温区温度y1的干扰进行补偿，使得u2对第一温区的影响为0；模糊解耦补偿器2将第一温区控制量u1对第二温区温度y2的干扰进行补偿，使得u1对第二温区的影响为0，这样就实现了被控对象输入、输出间的解耦控制。对质子交换炉2个温区可分别进行模糊补偿器设计，设计方法相同，为说明方便，去掉标识数字，模糊补偿器的原理如图3所示。

图3中的知识库框内包含隶属函数库μ、控制规则库R、清晰化方法库fd。本文所设计的模糊补偿控制器输入为预测控制器的输出控制量u和控制量变化du/dt，输出为u*。模糊补偿控制器的核心由模糊化模块(D/F)、近似推理模块(A*·R)、清晰化模块(F/D)组成。为了能够和输入、输出的清晰量相匹配，在模糊化模块之前设有量化因子ku、kuc，在清晰化模块之后有比例因子ku*。

本文设计的模糊补偿器输入输出量均取7个语言值{NB，NM，NS，ZO，PS，PM，PB}，模糊子集的论域均为{-6，-5，-4，-3，-2，-1，0，+1，+2，+3，+4，+5，+6}，其隶属度函数均采用对称三角形。结合质子交换炉实际的温度控制特性，根据已有的知识和经验，综合分析后得出控制决策，并总结出模糊控制规则表，如表1所示。

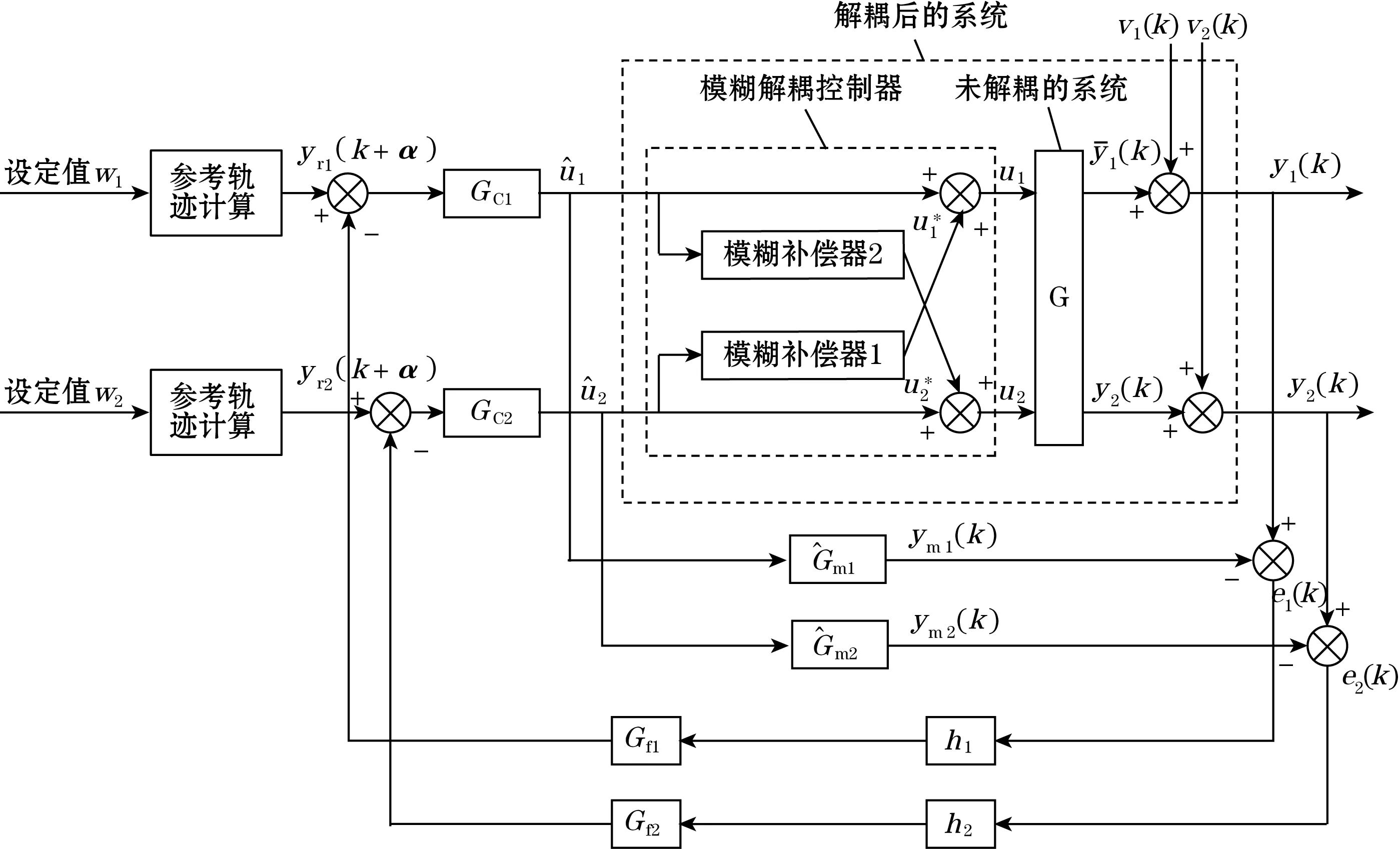
图2 模糊解耦与预测控制相结合的设计框图

图3 模糊补偿器原理框图

表1 补偿模糊控制器的模糊规则

本文采用Mamdani模糊模型的推理方法，根据当前时刻模糊控制的输入变化量量化值得到相应的隶属度值，再找出相关的模糊控制规则，即可得到控制量的输出模糊集。由于被控对象只能接受一个控制量，因此采用加权平均法从输出模糊集中计算出精确的控制输出量，其表达式为

(13)

式中：n为模糊变量的个数；μj为模糊变量；A(μj)为对应模糊变量的隶属度。

2.2 预测控制器的设计

模糊解耦控制器将多变量系统控制转化为2个单变量系统的控制，为了减弱控制效果对扰动的敏感程度，提高系统的抗干扰能力，在模糊解耦的基础上对系统采用预测控制算法，预测控制算法采用模型算法控制(model algorithmic control，MAC)，主要包括预测模型、在线校正、滚动优化等几部分，基本思想是首先利用预测模型预测系统未来的输出状态，再确定当前时刻的控制动作，具有预见性[16]。

对质子交换炉第一温区、第二温区可分别进行控制器设计，设计方法相同。解耦后的质子交换炉输出预测记为ymj(k+α)。

参考轨迹设计是预测控制算法中比较重要的一个环节。设wj为系统期望输出，为使系统平稳快速地达到系统给定值，预测控制的参考轨迹采用如下形式：

(14)

式中β为柔化因子，影响系统鲁棒性，β值越大鲁棒性越好，但是系统的响应也越慢。

由于系统存在非线性、时变及干扰等因素，因此必须用校正方法对基于预测模型得到的输出预测值进行校正，以提高预测值的准确性[16]。

ypj(k+α)=ymj(k+α)+[yj(k)-ymj(k)]

(15)

式中：ypj(k+α)为经校正后的α步超前预测输出；ymj(k)为k时刻预测模型输出；yj(k)为k时刻输出实测值。

选取系统的性能指标为

(16)

3 质子交换炉温度控制系统仿真分析

为了验证本文所提控制方法的有效性，使用MATLAB软件，在工作点对质子交换炉进行了控制仿真研究。第一和第二温区的温度设定值均为240 ℃，分别采用PID控制、单纯模糊解耦、模糊解耦控制与预测控制相结合这3种控制方法进行仿真研究，比较三者的控制效果。

3.1 解耦效果对比

为研究系统内的耦合，在80 s时给第一温区温度控制过程通道添加一个幅值为1的阶跃输入扰动；当系统运行到150 s时，系统运行稳定，此时给第二温区温度控制过程通道添加一个幅值为-3的阶跃输入扰动。2种控制方法的解耦效果对比如图4所示，图4(a)为第一温区加干扰时第二温区的温度变化，图4(b)为第二温区加干扰时第一温区的温度变化。

(a)第一温区加干扰时第二温区温度的变化

(b)第二温区加干扰时第一温区温度的变化图4 3种控制方法的解耦效果对比

通过对比图4(a)、图4(b)可以看出：相比较PID控制和单纯模糊解耦控制，模糊解耦与预测控制相结合的方法具有较强的解耦能力。当分别给2个回路加扰动时，使得扰动对另一回路温度输出的影响几乎为0，相比常规PID控制明显降低，展现了模糊解耦与预测控制相结合方法的解耦优势。

3.2 抗干扰效果对比

给某一温区加干扰时，除了对相邻温区的温度产生耦合影响外，还会造成自身温区温度的波动，如图5所示，图5(a)为第一温区加干扰时第一温区温度的变化，图5(b)为第二温区加干扰时第二温区温度的变化。

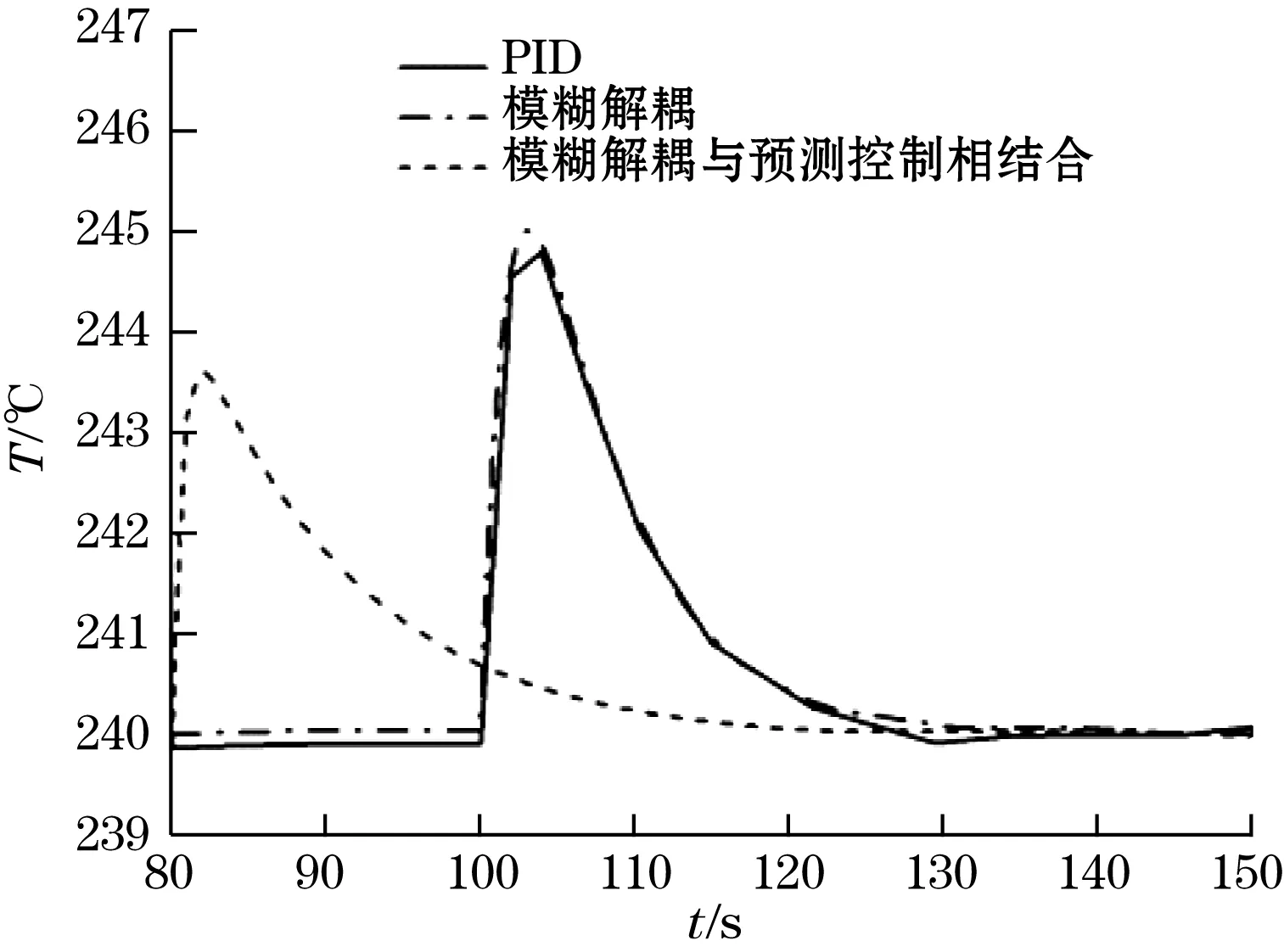
(a)第一温区加干扰时第一温区温度的变化

(b)第二温区加干扰时第二温区温度的变化图5 3种控制方法的抗干扰效果对比

通过图5(a)、图5(b)可以看出，采用单纯模糊解耦控制时，扰动引起自身温区的温度波动与PID控制相比没有明显改善，说明模糊解耦控制不能减小扰动引起自身温区的温度波动；而相比较PID控制和单纯模糊解耦，模糊解耦与预测控制相结合的方法明显减小了扰动引起自身温区的温度波动，2个温区的超调量分别从2.1%降低到1.4%、从6.3%降低到4.3%，提高了温度稳定性。同时从图5(a)可以明显看出，模糊解耦与预测控制相结合的方法能够实现系统的超前调节，这是由于加入预测控制会对系统未来输出有预测作用。

4 结论

本文基于热平衡机理建立了质子交换炉温控系统的数学模型，在此基础上提出了模糊解耦与预测控制相结合的控制策略。仿真结果表明，与传统PID控制和单纯模糊解耦控制相比，这种控制策略不仅能够降低系统耦合程度，而且减小了扰动引起自身温区的温度波动，控制效果明显改善。此外，模糊解耦与预测控制相结合的策略由于对系统未来输出有预测作用，能够对加热炉这一类时滞较大的系统实现超前调节，展现了所提策略的工程应用优势与价值。