基于分位数回归森林+POT的极端VaR风险测度
2022-10-13董皓天黄聪聪
蔡 超,董皓天,黄聪聪
(山东工商学院 统计学院,山东 烟台 264005)
一、引言
金融市场的稳健发展对经济发展有促进作用,金融市场风险的监管一直受到相关部门的重点关注。随着经济全球化的加速,金融市场的风险也越来越大,不可控因素也越来越多,比如1997年亚洲金融风暴,2008年全球金融危机,2015年中国股市市值暴跌,这些极端性的风险发生的频率在增加,导致的破坏性也在增加。如何精准地预测这些极端的金融风险,提前获知风险发展的动向,针对性的应对危机的发生是目前金融部门的重点问题。
在微观审慎监管框架下,经典的金融风险管理工具风险价值(VaR, Value at Risk)自从提出之日起,就受到了学界与业界的广泛关注。Jorion认为VaR风险实质为损失分布在某一置信水平下的分位数,可以通过优化非对称绝对损失函数得到[1]。基于此,在VaR风险测度中,Koenker等提出的分位数回归方法[2]起到了至关重要的作用。近年来,在非线性VaR风险测度方面,也取得了一些研究进展,主要有两类。第一类,参数形式的测度方法,如Engle等建立了CAViaR模型,使用非线性函数设定,进行非线性VaR风险测度[3];叶五一等分别使用门限分位数回归和动态分位数回归对VaR风险进行测度[4-5]。第二类,非参数形式的测度方法,如Taylor、许启发等使用神经网络分位数回归[6-7],Shim、许启发等使用支持向量分位数回归[8-9],Jiang、苟小菊等使用分位数回归森林,对VaR风险进行测度[10-11]。上述文献表明,在VaR风险测度方面非参数形式的分位数回归方法优于参数形式的方法。
虽然非参数分位数回归方法在测度VaR风险方面取得了较好的效果,但是Schaumburg认为由于极端尾部较少观测值会对非参数分位数回归的估计结果产生影响,使用非参数分位数回归方法并不能很好的测度极端VaR风险[12]。极值理论POT方法被广泛应用于金融数据尾部风险预测,如顾正娣和秦学志等使用POT方法测度了极端金融风险,发现其能够实现极端风险的有效测度[13-14]。本文结合QRF方法和POT方法的优点构建QRF+POT方法,一方面,利用集成模型比单一模型可以取得更好预测效果的优势,使用分位数回归森林这一集成模型来测度VaR风险的非线性结构;另一方面,使用POT方法来解决金融数据极端尾部观测值有限的问题。QRF+POT方法的基本思想为:首先,通过QRF方法得到正常分位点处的分位数估计;其次,通过POT方法将正常分位点处的分位数转化为极端分位点处的分位数,进而测度极端VaR风险。本文以上证综合指数、上证180指数、沪深300指数和深证成份指数的日收益率数据为研究对象,使用QRF+POT方法测度了极端VaR风险,并与QRT+POT方法、许启发等[15]提出的QRNN+POT方法进行对比,结果表明:与QRT+POT和QRNN+POT方法相比,在极端VaR风险测度方面,QRF+POT方法的表现更优,可以有效的描述收益率出现较大跌幅时的极端风险特征。
二、模型与方法
(一)VaR风险与分位数回归
t时刻的收益率yt可以定义为:
yt=100×(lnpt-lnpt-1),
(1)
其中,pt为第t天的价格。
收益率yt的相反数可以视为损失,即Lt=-yt。在置信水平100×(1-τ)%下,VaR可表示为:
VaR1-τ(Lt)=-inf{x|P(yt≤x)≥τ}=-Qyt(τ),
(2)
其中,τ(0<τ<1)为分位点,inf为下确界,P(·)表示概率。由式(2)可知,在给定置信水平下,VaR为收益率yt的τ分位数的相反数。对下述公式进行优化即可获得收益率yt的τ分位数:
作为一种非常古老的海洋动物,早在寒武纪时期,鲎就已经出现在地球上了,而且至今仍保持着“当年”的形态,堪称海洋世界里的“远古遗民”。为什么和它同时代的动物大都灭绝了,唯独鲎幸存下来了呢?
(3)
其中,损失函数ρτ(u)=u(τ-I(u<0))为分段线性函数,I(·)为示性函数。
(二)分位数回归森林模型

(4)
假设生成K颗决策树构建随机森林,则对于每个样本xi,随机森林的权重向量为各个决策树的平均:
(5)
随机森林使用决策树的平均结果来估计条件均值E(Y|X=x),即随机森林的预测值是响应变量的加权平均:
(6)
在展示了随机森林如何估计自变量的条件均值之后,将上述方法推广到整个条件分布,得到:
F(y|X=x)=P(yi≤y|X=x)=E(I(yi≤y)|X=x)。
(7)
条件分布的估计可以看成对于示性函数I(yi≤y)的加权平均。因而给出对于条件分布的估计为:
(8)
则τ条件分位数Qy(τ|X=x)为:
(9)
(三)POT极值方法
(10)
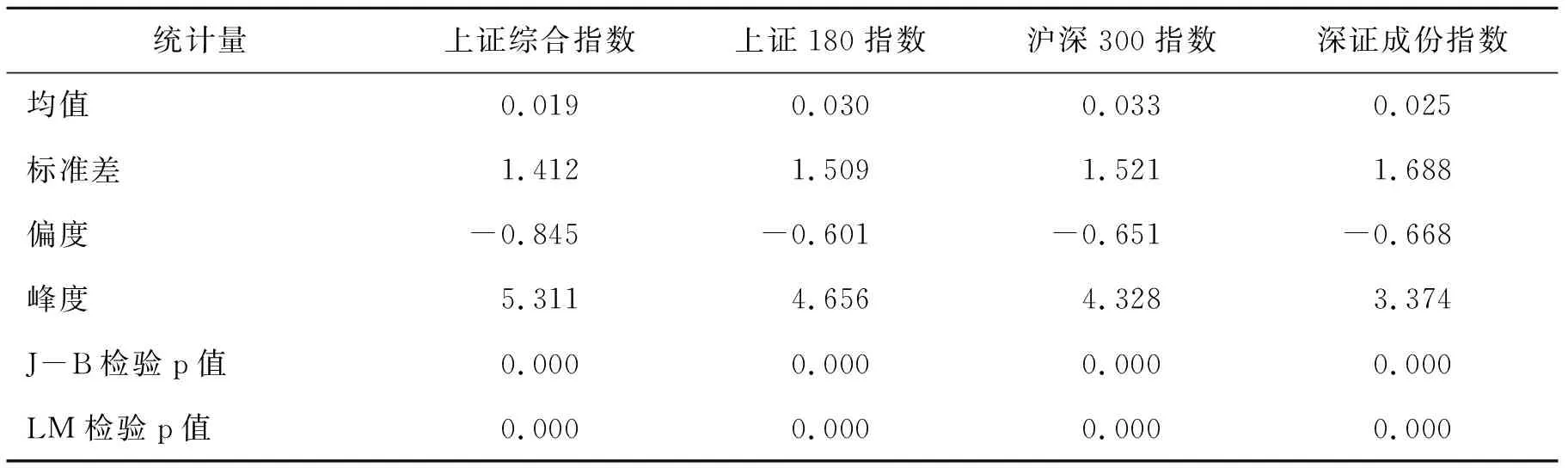
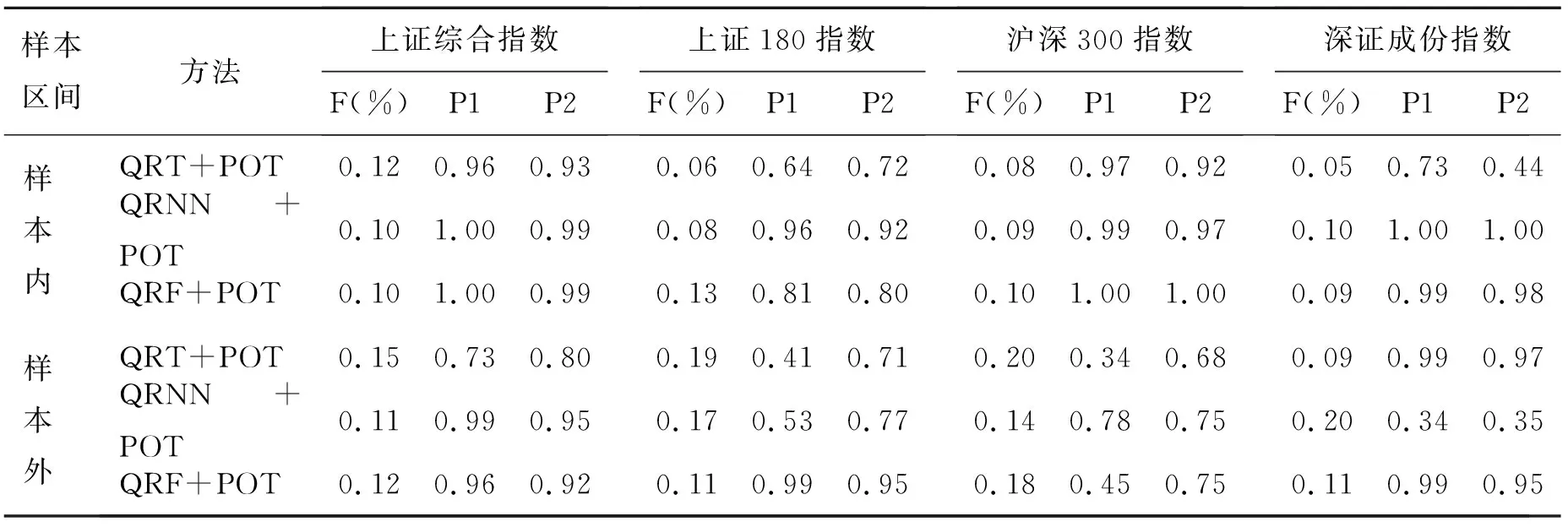
其中,0≤x 当μ→yF时,Fu(x)可以近似的表示为广义的帕累托分布: (11) 其中,ξ为形状参数,σ为尺度参数。即: Fμ(x)≈Gξ,σ(x)。 (12) 将式(12)代入式(10)可得: 1-F(x+μ)≈(1-F(μ))(1-Gξ,σ(x))。 (13) 设Nμ表示超出阈值的观测值数量,n是观测值总数,则(1-F(μ))=Nμ/n。对于式(13),令y=x+μ,将式(11)代入式(13),当ξ≠0时,尾部概率为: (14) τ分位数即为式(14)F(y)=τ的逆函数 (15) 实际中,通常需要估计τ=0.01或τ=0.001的极端分位数来测度在99%或99.9%置信水平下的极端VaR风险。然而,金融时间序列数据的尾部数据通常较少,分位数回归森林等传统的估计方法并不能获得较好的测度效果。因此将分位数回归森林与POT方法相结合构建QRF+POT方法估计极端分位点处的分位数,从而测度极端VaR风险。QRF+POT方法的具体步骤如下: 步骤1,运用QRF方法,估计正常分位点τ1处的分位数Qyt(τ1)。 步骤2,Qyt(τ1)根据计算分位数残差序列并对其进行标准化处理: (16) 步骤3,设极端分位点τ2(τ2<τ1)处的分位数为Qyt(τ2),则: (17) 由于Qyt(τ1)<0,式(17)中不等式符号发生改变。将式(16)代入式(17)可得: (18) 将式(18)计算逆函数可以得到: (19) 则极端分位数Qyt(τ2)和正常分位数Qyt(τ1)之间的对应关系为: Qyt(τ2)=Qyt(τ1)×[Qzt(1-τ2)+1]。 (20) 式中Qzt(1-τ2)是将zt中大于0的值代入式(11)计算形状参数ξ和尺度参数σ,再代入式(15)计算分位点(1-τ2)的分位数。 本文以上证综合指数、上证180指数、沪深300指数和深证成份指数的日收盘价数据为研究对象,时间跨度从2009年1月5日到2020年12月24日,共计2913天的数据,数据来源于国泰安数据库。日收益率用式(1)计算获得。表1给出了四支股票指数的日收益率的描述性统计结果。从表1可以看出,平均收益从高到低依次为沪深300指数、上证180指数、深证成份指数和上证综合指数;其标准差从高到低依次为上证综合指数、上证180指数、沪深300指数和深证成份指数,平均收益和标准差的表现符合“高风险-高收益”的规律。四支股票指数的偏度均小于0且峰度均大于3,尖峰厚尾特征明显。J-B检验和LM检验的p值均为0,表明指数收益率数据均不服从正态分布,且存在ARCH效应,具有异方差性特征。 表1 各股票指数日收益率的描述性统计结果 本文采用分位数回归树(QRT)、神经网络分位数回归(QRNN)和分位数回归森林3种非参数分位数回归方法测度VaR风险。为评价这3种方法对VaR风险测度的效果,首先,将日收益数据划分为样本内数据和样本外数据,样本内数据从2009年1月6日到2015年3月12日,共计1500天,样本外数据从2015年3月13日到2020年12月24日,共计1412天;其次,使用样本内数据建立模型;最后,分别使用样本内数据和样本外数据进行预测,比较3种方法的VaR风险测度效果。选取上述时间划分样本内数据和样本外数据的原因在于:2015年6月中国股市市值暴跌,跌幅达30%以上。因此,使用样本外数据来检验3种方法能否识别并预测出极端金融风险。在测度VaR风险的过程中,响应变量为yt,解释变量为滞后五天的收益率yt-1,yt-2,yt-3,yt-4,yt-5,主要考虑到滞后期的收益率对当期收益率的影响。 给定置信水平测度正常VaR风险,即估计时收益率分位数的相反数。为比较3种方法测度VaR风险的效果,对VaR进行返回测试,主要方法为模型失败率、似然比检验法[17]和有条件覆盖检验法[18],分别用符号F、P1和P2表示,结果如表2所示。 由表2可知,第一,在样本内和样本外中,3种方法都获得了较好的结果,表现为失败率都接近理论水平,且检验的P值都较大。这表明3种方法都是有效的。第二,与样本外的结果相比,样本内的失败率更接近理论水平,且检验的P值更大,这表明样本内的结果都优于样本外。第三,无论在样本内还是样本外,在大多数股票指数中,QRF方法VaR风险测度的失败率更接近理论水平,且检验的P值均高于QRT和QRNN方法,这表明QRF方法这一集成模型比其他两个单一模型具有更好的预测能力。 表2 95%置信水平下VaR返回测试结果 1.基于QRF模型的测度 给定置信水平1-τ=99%或1-τ=99.9%测度极端VaR风险,即计算τ=1%或τ=0.1%时收益率分位数的相反数。极端VaR返回测试的结果如表3所示(置信水平为99.9%的结果与99%的结果类似,因此文中只报告了置信水平为99%的结果)。由表3可知,第一,样本内的测度结果显示,QRT、QRNN和QRF方法在VaR的测度上都取得了较好的效果,失败率较为接近理论水平。第二,样本外的测度结果显示,各种方法的失败率都远大于理论值,且检验的P值都较小,这表明当发生股市市值暴跌的极端事件时,较少的极端尾部数据会导致各种方法预测能力显著下降,难以精确测度极端VaR风险。 表3 99%置信水平下极端VaR返回测试结果 2.基于QRF+POT方法的测度 表3的结果表明在极端风险突发的时期内,无论是集成模型还是单一模型都不能准确测度极端VaR风险。本节采用QRF+POT方法测度99%或99.9%置信水平下极端VaR风险,并与QRT+POT和QRNN+POT方法进行对比。表4和表5分别报告了基于POT方法的99%和99.9%置信水平下极端VaR风险的返回测试结果。由表4和表5可以看出,第一,在样本内和样本外,失败率都在理论水平的左右,且检验的P值都较大,这表明在极端VaR风险测度方面,结合POT方法的非参数分位数回归方法都优于单一的非参数分位数回归方法,也即结合POT方法处理极端尾部数据的能力有助于提高各种非参数分位数回归方法测度极端风险的精度。第二,与QRT+POT和QRNN+POT方法相比,QRF+POT方法的失败率更接近理论水平,且检验的P值更大,这表明QRF+POT方法在极端金融风险测度上优于QRT+POT和QRNN+POT方法。 表4 基于POT方法的99%置信水平下极端VaR返回测试结果 表5 基于POT方法的99.9%置信水平下极端VaR返回测试结果果 本文结合分位数回归森林和极值理论两个方面的优势,提出了测度极端VaR风险的新方法:QRF+POT。以上证综合指数等四支股票指数为研究对象,实证比较了QRF、QRF+POT与其他方法在样本内和样本外数据中的VaR风险测度效果,结果表明:第一,在正常VaR风险测度中,不管是单一模型的分位数回归方法还是集成模型的分位数回归森林都能较为准确的测度VaR风险,不过在样本内和样本外的结果中,分位数回归森林模型表现都优于单一模型的分位数回归方法。第二,在极端VaR风险测度中,无论是单一模型的分位数回归方法还是集成模型的分位数回归森林在样本外都表现不佳,不能实现准确测度。第三,在样本内和样本外,QRF+POT方法都能显著提高极端VaR风险测度的精度,且优于QRT+POT和QRNN+POT方法。 未来的研究中,一是考虑选取其他的极值理论方法,如EVT方法与分位数回归森林相结合测度极端VaR风险;二是将随机森林推广到expectile回归的框架下,构建expectile回归森林,用于ES风险的测度。三、实证研究
(一)数据的选取和统计分析
(二)正常VaR风险测度

(三)极端VAR风险测度


四、结论与启示
