时间积分方法的研究进展与挑战

邢誉峰 季奕 张慧敏

(1. 北京航空航天大学 固体力学研究所, 北京 100083;2. 北京理工大学 宇航学院, 北京 100081; 3. 北京宇航系统工程研究所, 北京 100076)

时间积分方法[1](time integration method,TIM)是求解动力学常微分方程最有力的数值方法之一,也是目前计算机辅助工程(computer aided engineering, CAE)软件中的主流时域求解器。 时间积分方法的思想[1]是:将待求时间域离散成为一系列时间区间或时间单元,并建立每个时间区间内位移、速度和加速度随时间的变化规律,进而由前一时刻的已知状态变量递推计算当前时刻的未知状态变量。 由此可见,时间积分方法有2 个特点[1]:①动力学平衡方程仅在离散时间点或广义时间点上得到满足,而不是在任意时刻都成立;②需要构造状态变量在时间区间或时间步内的变化规律。 这些变化规律决定一个方法的精度、耗散、效率和稳定性。 这与空间有限元方法类似,也需要设计单元的容许位移函数。 也就是位移随着空间坐标的变化规律,并且代数平衡方程也仅在结点上得到满足。 有限单元的容许位移函数决定了精度、效率和适用性。

级数展开法、Runge-Kutta 法和Newmark 方法是经典的时间积分方法。 基于级数展开思想直接构造的格式皆属于条件稳定的显式时间积分方法,代表性工作有Taylor 级数法和Lie 级数法。Taylor 级数法直接对时间坐标求导,而Lie 级数法则对状态变量求导。 求导方式的不同使得Lie 级数法可以解决Taylor 级数法中高阶求导困难和计算量大的问题。 Runge-Kutta 法是基于Taylor 级数展开思想于19 世纪末、20 世纪初提出的高精度方法。 Runge-Kutta 法[2]的求解对象是形如dz/dt=f(z,t)的一阶常微分方程(ordinary differential equation, ODE),其利用函数f在若干时间离散点上信息的线性组合来表示f的导数,再利用Taylor级数法确定其中的系数。 与级数展开法和Runge-Kutta 法不同,虽然Newmark 方法设计思想也是基于级数展开,但其求解对象为二阶ODE。Newmark 方法包括许多著名的辛格式,如梯形法则(trapezoidal rule, TR)、中心差分方法(central difference method, CDM)、Fox-Goodwin 方法等。

随着科学技术的发展,人们对时间积分方法的精度、效率、耗散和稳定性的要求越来越高,经典方法已经难以满足需求,这推动了时间积分方法在过去几十年中的持续发展。 激发人们设计高性能时间积分方法的主要问题可以概括如下:

1) 具有数值耗散的Newmark 方法[1]只有一阶精度。

2) 收敛阶数大于2 时,线性多步法只能是条件稳定或不稳定[3]。

3) 对线性系统具有无条件稳定性的二阶Newmark 辛几何方法,如TR,对于简单的非线性问题可能发散[4-5]。

4) 如何同时提高时间积分方法的精度、效率、耗散性能和稳定性。

5) 对非线性动力系统而言,时间积分方法的失稳机理,二阶非线性系统的无条件稳定性方法的设计原则。

针对问题1,通过对动力学平衡方程进行加权处理[6-10],或在差分格式中引入辅助状态变量[11-12],学者们发展了参数类耗散方法,该类耗散方法具有二阶精度。 为了解决问题2,学者们利用微分求积法[13-15]和加权残量法[16-18]等构造出了具有无条件稳定性的高阶时间积分方法。 针对问题3,借助能量有界准则[19],学者们发展了可稳定计算非线性动力响应的保能量方法[20-30]。为了全面提高时间积分方法的数值性能,通过使用更多时刻的已知状态变量,或不同分步采用不同类型的时间积分方法,学者们提出了线性多步法[31-38]和复合方法[39-50],这2 类方法可有效解决问题4。 问题5 更具有挑战性。 为了提高稳定性,学者们提出了结构相关时间积分方法[51-54],在该类方法中,算法参数与系统质量、阻尼和刚度矩阵相关,数值结果表明,该类方法能够有效提高数值积分方法处理软刚度系统时的稳定性。 此外,学者们还发现可利用幅值有界准则[55]或时变参数[31]解释在求解非线性问题时已有时间积分方法的失稳机理,并据此幅值有界准则设计了对一阶和二阶ODE 都是无条件稳定的BN 稳定型方法[56]。

本文着重介绍了针对上述问题提出的先进时间积分方法的发展状况,并对时间积分方法的未来发展趋势进行展望。

1 参数方法

为了提高Newmark 方法耗散格式的收敛阶次,学者们基于Newmark 方法发展了具有数值阻尼的二阶参数方法。 根据构造方式不同,参数方法可以分成2 类:一类是加权动力学平衡方程,另一类是在差分格式中引入辅助变量。

第一类参数方法的代表性工作有广义-α方法[6-8]、HHT-α方法[9]和WBZ-α方法[10]。 这类方法沿用了Newmark 方法的差分格式,即

式中:M、C、K和R分别为质量矩阵、阻尼矩阵、刚度矩阵和外载荷列向量。

由式(2)可以看出,第一类参数方法不满足离散时间节点的平衡方程。 广义-α方法的参数可统一写成高频极限处谱半径ρ∞的函数,即

上述参数可保证广义-α方法具有二阶精度,并且高频段的数值耗散程度可由ρ∞精确调控。当α=δ=0 时,广义-α方法退化为Newmark 方法;当α=0 时,广义-α方法退化为HHT-α方法;当δ=0 时,广义-α方法退化为WBZ-α方法。 以广义-α方法为代表的第一类参数方法采用了加权思想,使得动力学平衡方程不能被严格满足,这导致由该类参数方法计算的加速度仅具有一阶精度。 为了改善该性能,张慧敏和邢誉峰[11]提出了第二类参数方法,其在时间节点处严格满足动力学平衡方程,即

因此,该类方法被称为三参数单步法(three parameters single-step method, TPSM)。 引入的辅助变量θ是一个中间变量,其本身不需要满足任何状态方程。 因此,在初始时刻,θ可以设置为0以避免额外的启动程序。 采用相同的构造方式,邢誉峰和张慧敏[12]还发展了四参数保辛单步法(four parameters single-step method, FPTM)。

2 高阶无条件稳定方法

通过减小时间步长来提高精度最容易实现,这相当于有限元方法中的h收敛性,但不可避免会导致计算量增加,而且会引入舍入误差。 升高时间积分方法的收敛阶次是另一种提高计算精度的有效方式,相当于有限元方法中的p收敛性。虽然线性多步法的稳定性受Dahlquist 定理[3]的约束,即当收敛阶次大于2 时,算法是条件稳定或不稳定,不过学者们利用多级升阶思想构造出了具有无条件稳定性的高阶时间积分方法。

多级方法的定义是:在每个时间步内,在多个时刻或多次在同一时刻满足动力学平衡方程的时间积分方法。 代表性工作有Runge-Kutta 法[2]、微分求积法[13-15]和加权残量法[16-18]等。 多级方法的稳定性不受Dahlquist 定理约束,可以同时实现高阶精度和无条件稳定性,随着算法级数的增加,方法的收敛阶次随之提高,但伴随着成倍增加的计算量。

基于多级思想建立的Runge-Kutta 法[2]因其精度高而被广泛用于求解一阶ODE。 若用其求解二阶ODE,则需将二阶ODE 转化为一阶ODE。Runge-Kutta 法按构造格式可以分为显式、对角隐式和完全隐式3 类。 利用高斯积分,s级完全隐式Runge-Kutta 法可以达到2s阶精度。 但是,如此改善精度导致计算成本大幅度增加,因此其实用价值不高。 综合精度、效率和稳定性,对角隐式Runge-Kutta 法更受欢迎。 Runge-Kutta 法的求解格式为

由式(8)可以看出,对角隐式Runge-Kutta 法的系数矩阵A是一个对角元素不全为0 的下三角矩阵。 通过参数设计和选择足够的级数,隐式Runge-Kutta 法可以具有任意高阶精度和无条件稳定性。

基于微分求积思想、加权残量思想、最小二乘法等,Fung[13-14,16,18]构造出一些高阶无条件稳定方法。 在Fung 的工作基础上,一些性能更加优秀的高阶方法被提出,如Huang 方法[57]和Kim 方法[58]。 Huang 和Fu[57]将不同格式的Fung 方法混合使用在一个时间步长内,从而有效提高了低频精度。 在不损失高阶精度和无条件稳定性的前提下,Kim 方法[58]优化了一个时间步内时间离散点的位置,使得最后一个时间配点与时间步的终点重合,从而简化了Fung 方法的执行流程。 下面以Kim 方法为例,简述该类高阶方法的构造流程。 在Kim 方法中,位移、速度和加速度的表达式如下:

式中:ψj为第j个时间点的Lagrange 插值函数;uj、vj和aj分别为第j个时间点的位移、速度和加速度。

Lagrange 插值函数的定义为

式中:tk为第k个时间步的初始时刻;τs和Δt为第k个时间步内的配点。

在式(9)中,位移、速度和加速度是彼此独立的。 Kim 方法采用加权残量法建立速度-位移和加速度-速度之间的关系,即定义如下残量:

结合t+τiΔt(i=1,2,…,n)时刻的动力学平衡方程,即可求解出所有未知的状态变量。 基于微分求积思想、加权残量思想、最小二乘法等建立的高阶方法在有数值耗散时具有(2n- 1)阶精度,在无数值耗散时是2n阶精确的。

3 保能量方法

著名的TR(即欧拉中点辛差分格式)谱半径特性表明其是一种无条件稳定方法,但将其应用于求解一些简单的非线性问题时,如刚性单摆[4]和软弹簧方程[5],发现若时间步长选取的不合适,TR 会发散。 虽然数值阻尼可以增强稳定性,但当把耗散方法用于非线性问题求解时,其结果仍可能不收敛。

为了稳定地计算非线性动力学响应,学者们基于能量有界准则[19]建立了保能量方法。 在该类方法中,当前时间步的机械能小于或等于上一时间步的机械能与外力功之和。 据此准则,Hughes 等[22]首先提出了约束能量型方法(constraint energy method, CEM)。 CEM 以TR 为 基础,通过Lagrange 乘子法施加能量准则约束。 然而,该方法需要额外计算Lagrange 乘子和离散的能量值,在非线性迭代中还会遇到收敛困难问题。不同于CEM,Simo 和Wong[30]提出了另一种保能量方法,即能量-动量法(energy momentum method, EMM)。 EMM 是基于修正的中点法则建立的,在使用Green 应变的非线性系统中可以保守能量,但其难以推广到一般非线性系统。

针对一般非线性系统, 已有 Gonazlez 方法[26]、Krenk 方法[25]等。 这些方法均基于中点法则,修正后的中点内力能够满足能量守恒的要求,但也都需要计算离散点的能量值。 为了解决这个问题,笔者直接从能量准则出发,提出了一种更为通用的保能量方法[21](energy-conserving method,ECM)。 该方法利用Gauss-Legendre 求积法则计算平均内力,数值结果表明,只要使用足够的节点数,就可以精确地保守系统能量。 更重要的是,该方法仅需已知内力形式即可,不需要计算能量,并且适用于同时包含阻尼和刚度非线性的动力学系统。

下面以CEM 为例,简述保能量方法的实现过程。 考虑如下非线性保守系统:

式(17)是所有保能量方法的设计准则。

CEM 是基于TR 设计的,对于方程(14),其递推格式如下:

在CEM 中,定义一个泛函Γ(xt+Δt),其形式如下:

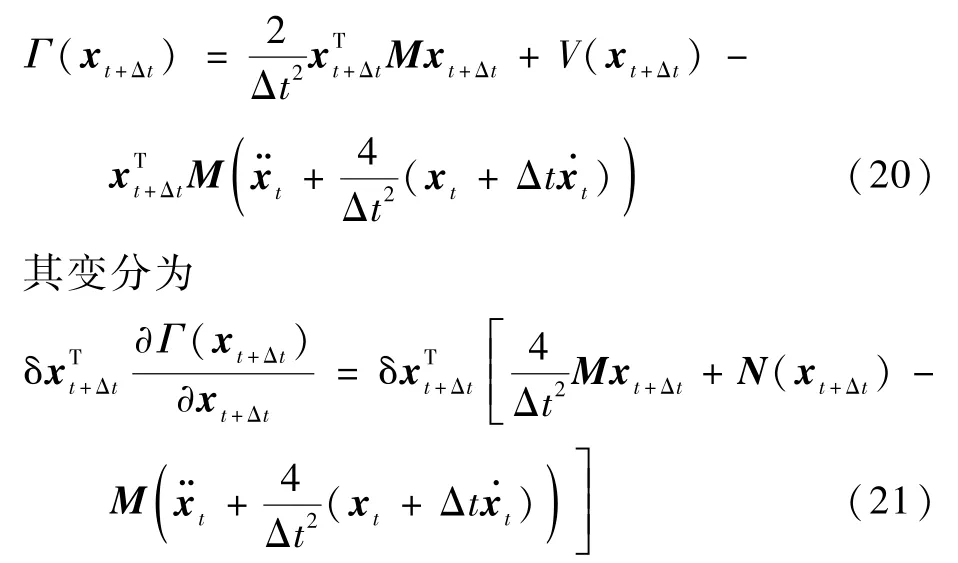
由式(21)可见,式(18)等价于泛函Γ(xt+Δt)的一阶变分等于零。 为了满足能量守恒方程(17),CEM 将Γ(xt+Δt)修正为

通过式(23)和式(24)可联立求解出xt+Δt和λ,进而利用式(19)计算t+Δt时刻的速度和加速度。 从方程(24)可以看出,每一步CEM 都需要计算能量,与TR 相比计算量略有增加。

4 线性多步法和复合方法

为了综合提高时间积分方法的数值性能,包括精度、效率、耗散和稳定性,可以采用线性多步法和复合方法。 线性多步法属于单步时间积分方法中的一种,但为了计算当前时刻的响应xt+Δt,需要利用其他自启动方法计算前几个时刻的响应,以获得足够的启动信息。 与线性多步法不同,复合方法是将一个时间步划分成若干个分步,计算xt+Δt需要每个分步的信息。

4.1 线性多步法

工程界目前使用较多的线性多步法[2]有Adams 类方法、显式Adams-Bashforth 方法、隐式Adams-Moulton 方法及预测校正类格式等。 这些方法虽然具有高阶精度,但稳定性难以提高。 Dahlquist[3]曾证明,所有显式方法和二阶以上的线性多步法均无法实现无条件稳定。 因此,在实际应用中,显式和隐式线性多步方法常作为预测和校正方法成对使用,并结合自适应步长技术,控制局部截断误差,以避免结果发散。 此外,向后差分格式,如Houbolt 方法[59]和Park 方法[1],也属于经典的线性多步法。 它们一般具备二阶精度、无条件稳定性及强烈的高频耗散能力,可以快速滤掉高频响应成分,因此更适用于刚性动力学系统的分析。

为进一步提高线性多步法的计算精度,学者们构造出了更加精确的线性三步法[33]和线性四步法[33]。 另外,为了解决线性多步法无法自启动的问题,通过引入一些辅助状态变量,学者们还提出了与一些线性多步法具有相同数值性能的单步法[32-33]。

下面以线性两步法[33](linear two-step method, LTM)为例,介绍该类方法的求解流程。 LTM的递推格式为

由式(26)可以看出,LTM 需利用其他自启动方法计算t- Δt时刻的状态变量,之后才能执行式(26)。

4.2 复合方法

复合方法在一个时间步的不同分步内使用不同的时间积分方法,以发挥不同方法各自的优势,从而获得优于各分步方法的数值性能。

Bank 等[60]在1985 年把TR 和后向差分公式(backward difference formula, BDF)组合使用,并将其用于求解一阶ODE。 Bathe 和Baig[46]在2005 年将这种复合方法TR-BDF 用于求解二阶ODE,并发展了复合方法概念。 随后,Bathe 等进一步研究了TR-BDF 方法在非线性系统[61]、波传播[62]等问题中的性能。 TR-BDF 方法优越的低频精度和高频耗散能力受到了学术界和工程界的广泛关注。 在Bathe 方法基础上,学者们提出了一系列性能更加优越的复合方法,如三分步TR-TRBDF[50]、三分步TR-BDF-Houbolt[48]、四分步Optimal-TR-TR-TR-BDF[42]等。 与 两 分 步 Bathe 方法[46]相比,这些方法的低频精度更高。

由TR 和BDF(或Houbolt 方法)组合的复合方法具有L 型稳定性。 为了能够精确地调控高频段的数值耗散量,基于标准Bathe 方法[46],Rezaiee-Pajand 和Sarafrazi[37]提 出 了β1/β2-Bathe 方法,该方法的第二分步采用两点后向差分公式(backward interpolation formula, BIF),通过调整β1和β2的大小和比例,可以控制高频段的数值耗散量。 之后,Noh 和Bathe[44]进一步优化了β1/β2-Bathe 方法,提出了ρ∞-Bathe 方法,仅使用一个参数ρ∞来光滑和准确地改变数值耗散的大小。 在具有可控数值耗散的前提下,为了进一步提高该类方法的低频精度,季奕和邢誉峰[43]提出了一种优化三分步方法。

下面以Bathe 方法[46]为例介绍复合方法的求解思路。 在Bathe 方法中,把一个时间步[t,t+Δt]划分为2 个分步[t,t+γΔt]和[t+γΔt,t+Δt],其中γΔt表示第1 个分步的大小。 TR 被用在第1 个分步中,即

式中:θ0、θ1和θ2为算法参数。

联立求解t+γΔt和t+Δt时刻的动力学平衡方程,即可得到一个时间步内所有状态变量。

另外,针对由TR 和BDF(或BIF)复合得到的时间积分方法,邢誉峰和季奕等[42]研究了如何选择分步数、分步步长、差分点数、各分步采用的方法,并得到了一些重要的结论,为复合方法的构造提供指导,这些结论包括:

1) 当BDF(或BIF)采用的差分点数不变时,随着分步数的增加,TR 在一个时间步中的占比增加,从而提高了低频精度。 但是,这种方法不能明显提高低频精度。

2) 当分步数固定时,提高BDF 的差分点数(或BIF 中的插值点数),可以有效提高低频精度。 实际上,随着差分点数目增加,一个时间步内采用TR 的分步的占比略有降低。 因此,可以认为增加差分点数比增加分步数更有助于提高低频精度。

3) 当分步数为常数时,只要采用相同的参数优化方式,就可以构造出性能相近的复合方法。如三分步优化Optimal-TR-BDF-BDF 方法中采用TR 的分步的占比大约是三分步优化Optimal-TRTR-BDF 方法中的一半,但二者的计算精度几乎相同。

5 BN 稳定型方法

引入数值阻尼是改善时间积分方法在非线性系统中稳定性的一种直接且有效的方式。 与非耗散方法相比,一般情况下耗散方法在非线性系统中具有稳定性优势,但其精度变低。 为了保证在计算非线性动力学响应时的稳定性,保能量方法是一种选择。 但保能量方法具有额外的计算量,并且适用范围有限。

下面简单介绍ρ∞-TSSBN 方法的求解格式和算法参数。 该方法包含2 个分步[t,t+c1Δt] 和[t+c1Δt,t+c2Δt],其中,0 ＜c1＜c2＜1。 第1 个分步的求解格式为

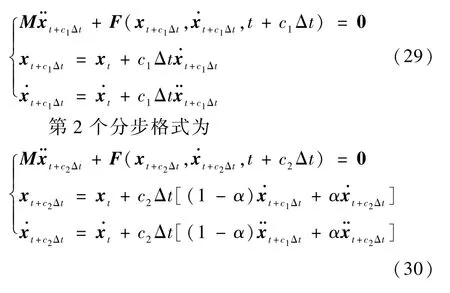
式中:F为包含内力和外力的向量。

由式(29)和式(30)可求解出t+c1Δt和t+c2Δt两个时刻的状态变量。 时间步终点t+Δt的信息是由这2 个时刻的状态变量加权得到,即

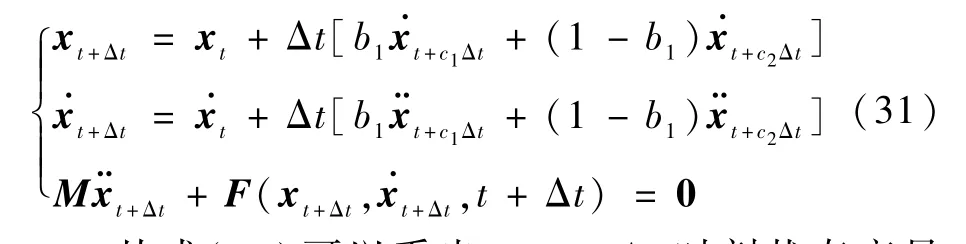
从式(29)可以看出,t0+c1Δt时刻状态变量的求解不需要初始时刻t0的加速度信息,因此,该方法是一种真正的自启动方法。

从式(31)可以看出,t+ Δt时刻不需要有效刚度矩阵分解和Newton 迭代运算。 因次,从计算量的角度来说,该方法属于两分步格式。

为了确保ρ∞-TSSBN 方法能够稳定地处理非线性系统,即具有BN 稳定性,利用BN 稳定性理论的充分条件(即代数稳定性)设计了该算法参数。 当ρ∞=1 时,算法参数为

数值算例表明,在TR 和ρ∞-Bathe 方法失效的非线性问题中,ρ∞-TSSBN 方法可以给出稳定且精确的结果。

6 结束语

本文介绍了用于求解动力学常微分方程的时间积分方法,并着重介绍了近年来发展出的一些先进时间积分方法,包括参数方法、高阶无条件稳定方法、保能量方法、线性多步法、复合方法和BN稳定型方法。 更详细的资料读者可以阅读相关的综述文章[63]和专著[64]。

关于时间积分方法的未来发展问题,可以从其求解的是线性问题和非线性问题角度进行讨论。

对于线性动力系统,时间积分方法的设计已有成熟的理论基础。 虽然已经存在高精度、快速计算方法[65-67],但如何更快、更精确地计算仍然是人们追求的目标。 对于线性单自由度动力系统,已经可以利用时间积分方法得到精确的结点位移[68-69],其具有精确的幅值和相位。 对于线性多自由度系统,虽然辛几何算法[70]具有保幅值或保能量特性,或者说从根本上解决了幅值误差累计问题,但相位误差累计问题仍然存在。 幅值有界准则和能量准则都是针对幅值衰减和发散问题提出的,但建立一个针对相位误差的约束准则是值得探索的。

对于复杂非线性动力系统,时间积分方法的精度和稳定性应该是更加本质的问题。 季奕等[56]基于BN 稳定性理论已经设计出两分步二阶无条件稳定时间积分方法,但发展更精确高效的BN 稳定型方法是一项有意义和挑战的工作。此外,虽然季奕和邢誉峰[31]已经建立了时变参数谱分析理论,并利用此理论设计了对非线性刚度系统是无条件稳定的方法,但尚未将这种方法推广用于非线性阻尼系统等。 非线性系统的高阶时间积分方法的设计及多尺度快速计算问题等也都是值得关注的问题。

现代科学发展的特征是多学科交叉、多物理场耦合和多尺度分析和非线性特征,对于结构动力学系统时间积分方法的研究工作也要与现代科学发展的步伐协调一致。