复杂电磁环境辐射-散射耦合场快速预估方法

苏东林 崔朔 白江飞 李尧尧

(1. 北京航空航天大学 电子信息工程学院, 北京 100083; 2. 北京航空航天大学 前沿科学技术创新研究院, 北京 100083;3. 北京航空航天大学 沈元学院, 北京 100083)

随着电子信息技术与电子对抗技术的发展,在当前及未来的作战场景中,干扰辐射源和目标散射体同时存在,战场态势瞬息万变,电磁环境严酷复杂[1]。 为了分析、评估电子信息系统的复杂电磁环境适应性能力,掌握系统性能边界,对复杂电磁环境的数值模拟与仿真必不可少[2-3]。

目标电磁散射特性是影响目标回波幅度的关键因素,蕴含着目标的几何结构、材料等信息[4]。在目标电磁散射特性研究中,研究者提出了雷达散射截面(radar cross section,RCS)[5]、散射振幅系数[6]、极化散射矩阵[7-8]等描述参数,为散射特性问题的分析提供了可量化的概念。 在辐射研究中,天线远场辐射方向图[9-10]是表征辐射特性的典型特征。

研究者引入多种方法进行电磁场的仿真计算。 低频数值方法包括矩量法(method of moments,MOM)[11]、有限元法(finite element method,FEM)[12]和时域有限差分法(finite difference time domain,FDTD)[13]。 近似求解方法包括几何光学法(geometric optics,GO)[14]、物理光学法(physical optics,PO)[15-16]、弹跳射线法(shooting and bouncing ray,SBR)[17]、一致性几何绕射理论(uniform geometrical theory of diffraction,UTD)[18-20]等。 为了进一步提高计算效率、减少资源占用,研究者提出了多种加速技术,如快速多级子方法(fast multipole method,FMM)、多层快速多极子方法( multilevel fast multipole method,MLFMM)、矩阵预处理技术、递归方法、快速傅里叶变换方法等,来快速求解线性方程组[21-22],基于CPU/GPU 的硬件加速、树形数据结构快速检索技术等来快速追迹射线管[23],基于高斯回归预测、神经网络建模等策略来建立数学预测模型[24-25]。

就研究对象而言,上述描述方法或关注金属/介质结构的散射特性求解,或关注天线的辐射特性求解。 对于目标散射体和辐射源同时存在的复杂电磁环境,空间中既有辐射场,又有散射场,辐射场对目标的散射场、探测雷达的接收场均存在影响。 此时,雷达接收到的空间总场不能用目标单独存在时的散射场和干扰单独存在的辐射场直接叠加的方式来描述,还要考虑辐射源对目标的耦合散射场。 综上所述,面向辐射源和目标散射体共同存在的实际场景仿真的应用需求,仍存在一定研究空间:

1) 对抗场景中,雷达、目标散射体、干扰辐射源的相对态势瞬息万变,场景电磁环境的仿真预测需要具备近实时计算效率,常规的电磁计算方法难以满足要求。

2) 对于不掌握精确几何结构的非合作目标,传统的依赖目标和天线的几何模型的电磁计算方法存在应用困难。

3) 对于散射场与辐射场相互交织的复杂场景,传统的单独针对散射或辐射的计算不能描述辐射场与散射场间的物理作用,存在模型误差。

4) 动态场景中,孤立目标或干扰辐射源的位置和姿态变化,但散射和辐射特性不变,若能在场景电磁环境计算中利用这一特点,有望进一步节约资源、提升效率。

因此,本文提出一种辐射-散射耦合场快速预估方法。 首先,载入天线装机方向图和平台雷达散射截面数据;然后,通过射线定向和引爆计算辐射场对散射场的激励;最后,通过场的极化矢量叠加,得到辐射、散射耦合条件下的场景远场结果。本文方法将复杂电磁环境辐射-散射耦合场的计算与环境中目标的散射特性数据库和干扰的辐射特性数据库建立联系,在先验数据的支撑下,通过建立和调用对应的散射特性、辐射特性数据开展场景的电磁计算,实现了耦合散射场的实时预测。仿真结果验证了辐射源存在情况下,雷达接收的电磁场较目标原始散射场存在明显差异,从而将影响雷达正确识别目标。

1 辐射-散射耦合场模型

基于雷达视角,对包含干扰辐射源和目标散射体的复杂电磁环境进行分析,如图1 所示。

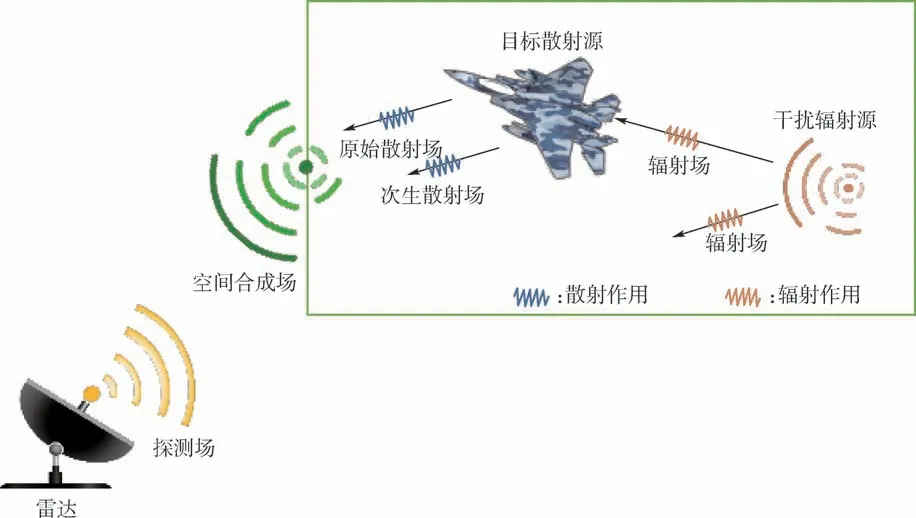
图1 辐射-散射耦合场景示意图Fig.1 Radiated and scattered coupled fields

空间存在的总电场E可分为4 类:雷达入射场Ei、目标在雷达照射下产生的原始散射场Es、散射体在辐射源照射下产生的次生散射场E′s及干扰辐射源产生的辐射场Er,即

1.1 目标原始散射场

目标原始散射场Es是目标散射体对雷达入射场Ei的响应。 从感应电流的观点分析,入射场在散射体表面激发感应电流Js,进而在空间形成散射场。

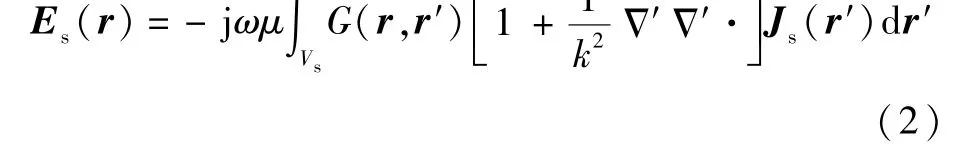
式中:ω为角频率;μ为真空磁导率;Vs为散射体;r和r′分别为场点和源点;G(r,r′)为自由空间点源格林函数;k为波数。

应注意的是,多散射体同时存在时,各散射体上的感应电流不等于它们孤立地被同样的入射场激发的感应电流。 原因在于:各散射体的散射场形成了新的激励源,影响其他散射体上的感应电流。

1.2 干扰源辐射场

实际中的干扰源辐射场通常来自于飞行平台上雷达和干扰机辐射的电磁场。 辐射源电流密度为Jr,则引发的辐射电场Er为

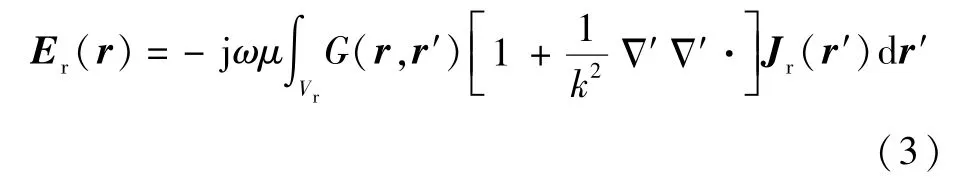
式中:Vr为干扰辐射源。

1.3 目标次生散射场

对于1.2 节所述的辐射场,当其照射到目标表面时,会在目标上激发感应电流,并产生散射场。 空间中的辐射场也会照射到目标表面,激发感应电流并产生散射场。 为与入射场激发的原始散射场相区分,辐射场激发的感应电流成为次生感应电流,辐射场激发的散射场称为目标的次生散射场。

照射到目标上的辐射场E′i(r)为

2 辐射-散射耦合场快速预估方法

实际工程中,单目标、单辐射源的特性数据往往都是具备的,这些数据中隐含了目标散射体和辐射源的几何外形、材料参数等特征信息。 利用这些已知先验信息,可以等效替代复杂环境求解中耗时的积分或路径寻迹步骤,直接实现辐射和散射电磁场的快速求解。

2.1 辐射场快速计算方法

2.1.1 远场方向图

天线远场方向图通常描述为

式中:Er为远区球面上任意(θr,φr)方向某点处的场强;Er,max为球面上Er的最大振幅。

2.1.2 辐射场的计算和变换

在干扰源天线处建立本地坐标系。 对于与干扰源天线相对方向相同的矢量,其在场景中干扰源天线在本地坐标系下的角度坐标与在干扰源天线远场方向图中的角度坐标一致。 干扰源天线本地角度坐标与全局角度坐标的转换关系详见2.2.2节。

借助天线远场方向图,局部坐标系下的干扰源辐射场Er,l的计算公式为

式中:α为电场幅度系数;^er,l为干扰源天线的电场单位矢量;r为空间场点,在干扰源天线局部坐标系中的角度坐标为(θr,l,φr,l);kr为干扰源辐射场波矢;ra为干扰源天线的等效相位中心;β为干扰源辐射场初始相位。

将该干扰源辐射场转换到全局坐标系下,表示为

2.2 散射场快速计算方法

2.2.1 极化散射矩阵

式中:Sij(i,j=θ,φ)为目标以i极化接收和j极化发射时的复标量散射系数,i、j代表2 个正交的极化基方向;θs和φs分别为散射方向的俯仰角和方位角;θi和φi分别为入射方向的俯仰角和方位角。

2.2.2 散射场的计算和变换

由于目标在场景中的姿态与其在极化散射矩阵数据库中的姿态不尽相同,为将目标极化散射矩阵中的角度与场景中的角度做对应,采用坐标系转换的方法。

建立场景的全局坐标系,记为O(^x,^y,^z)。 在目标处建立本地坐标系,记为r0(^u,^v,^w)。 对于与目标相对方向相同的矢量,其在场景中目标在本地坐标系下的角度坐标与在目标极化散射矩阵数据库中的角度坐标一致,如图2 所示。 本地坐标系基矢与场景全局坐标系基矢间的关系为

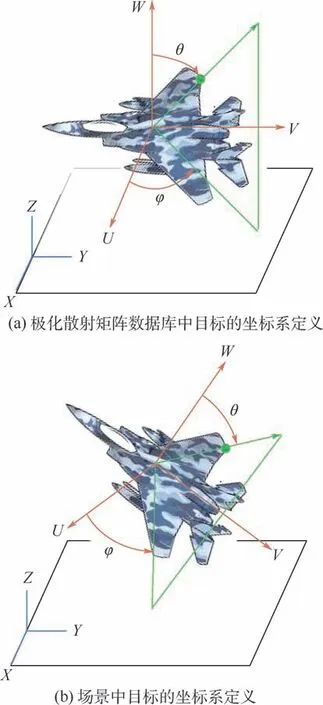
图2 极化散射矩阵数据库与场景中目标的坐标系定义Fig.2 Coordinate system definitions of polarization scattering matrix database and target in the scene

式中:ki为入射场波矢;r0为散射体位置矢量;Ei为场景的入射场场强;θ^i和^φi分别为全局坐标系中入射场的垂直极化方向基矢和水平极化方向基矢;θ^i,l和^φi,l分别为本地坐标系中入射场的垂直极化方向基矢和水平极化方向基矢。

假定入射场的源和目标的距离、接收天线和目标的距离均满足远场条件,借助极化散射矩阵,局部坐标系的远场散射场Es,l的计算公式为

式中:θs,l和φs,l分别为散射场波矢方向在目标本地坐标系中的俯仰角和方位角;θi,l和φi,l分别为入射场波矢方向在目标本地坐标系中的俯仰角和方位角;ks为散射场波矢;r为远场场点。

将该散射场转换到全局坐标系下,表示为

式中:θ^s和^φs分别为全局坐标系中散射场的垂直极化方向基矢和水平极化方向基矢;θ^s,l和^φs,l分别为本地坐标系中散射场的垂直极化方向基矢和水平极化方向基矢。

2.3 次生散射场快速计算方法

对于次生散射场,由于目标的极化散射特性不因入射场的变化而变化,仍可使用极化散射矩阵进行快速求解。

当散射体和干扰辐射源位置满足远场条件、散射体可近似为一点时,干扰源辐射场在散射体处可近似为沿连线方向传播的平面波。 此时,目标的次生散射场可表示为

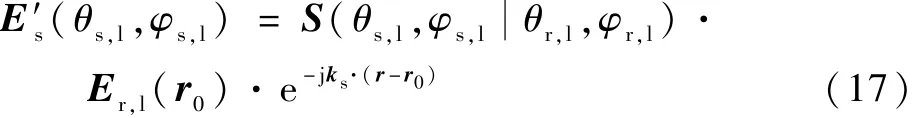
式中:θr,l和φr,l为干扰辐射源相对于目标的局部角度坐标;r为远场场点;Er,l(r0)为r0处的远场干扰辐射场。

2.4 场合成方法

为了计算辐射-散射矢量耦合场总场,本文方法对耦合场的各成分分量向全局坐标系下的极化基做投影,再按极化类型分别进行求和。

以2 个场成分为例。 将场1 整理为全局坐标系下的表达式为

3 仿真实验

建立理想导体球和电偶极子辐射源、飞机和喇叭天线辐射源2 个算例,分别就本文方法原理的正确性和方法的适用性开展验证。 所有仿真均在Intel(R) Core(TM) i7-7700 CPU@ 3. 60 GHz,16.0 GB RAM 的台式计算机上完成。

3.1 理想导体球和电偶极子辐射源

仿真场景设置如图3 所示。 位于XOY平面上的理想导体球半径为0.5 m,一个辐射源位于从球心沿Y方向相距D处,辐射源为偶极矩0.005 Am的理想电偶极子。 平面波从θi= 0°,φi=0°处入射。 仿真频率为300 MHz。

图3 理想导体球与电偶极子仿真场景示意图Fig.3 Simulation scene of a perfect conductor sphere and an electric dipole

图4 给出了不同距离D和辐射源强度倍数因子M时,整个场景的远场电场强度计算结果。以图4(a)为例,将商业软件feko 的MOM 求解器的求解结果作为参考值,本文方法的均方根误差为0.002 7,结果一致性良好。 每个三维全空间场景平均用时0.008 9 s。 可以分析得到以下规律:

图4 不同距离和辐射源强度倍数因子的理想导体球与电偶极子远场电场强度对比Fig.4 Comparison of far-field electric field strength of a perfect conductor sphere and an electric dipole at different distances and radiation source intensity multiplier factors

1) 在相同距离D下,辐射场的倍数因子M越大,空间总远场电场分布越接近电偶极子孤立存在时的辐射电场;辐射场的倍数因子M越小,空间总远场电场分布越接近理想导体球孤立存在时的散射电场。

2) 在相同辐射场倍数因子M下,距离D越大,空间总远场电场分布越接近此时场强相对较大的场成分。

这些规律符合物理规律,验证了本文方法的正确性。

3.2 飞机和喇叭天线辐射源

为了验证本文方法的实用性,对飞机和喇叭天线辐射源的场景进行计算。 仿真场景如图5 所示。 飞机等效相位中心位于ra=(xa,ya,za);辐射源为喇叭天线的辐射场,等效相位中心位于(0,0,0) m。 平面波从θi=90°,φi=30°处入射。 仿真频率为3 GHz。

图5 飞机与喇叭天线辐射源仿真场景示意图Fig.5 Simulation scene of an aircraft and a conical horn antenna’s radiated field

图6 给出了不同距离下,整个场景的远场电场强度计算结果。 以图6(i)为例,将商业软件feko的MOM 求解器的求解结果作为参考值,本文方法的均方根误差为0.000 09,结果一致性良好。每个三维全空间场景平均用时0.009 5 s,与3.1 节场景算例的计算效率持平。 通过对结果分析可以发现,辐射场强度和位置均会对空间中的场分布产生显著影响。 其中,辐射场强主要影响目标回波散射场强度,辐射场位置主要影响目标回波散射场分布。

图6 不同距离和辐射源强度倍数因子的飞机与喇叭天线辐射源远场电场强度对比Fig.6 Comparison of far-field electric field strength of an aircraft and a conical horn antenna’s radiated field at different distances and radiation source intensity multiplier factors

4 结 论

区别于经典的计算电磁学计算方法,本文提出了一种辐射-散射耦合场快速预估方法,适于工程应用。

1) 利用提前获取并加载的天线辐射方向图和目标极化散射特性数据,能够实现对复杂电磁环境近实时预测,适用于动态电磁环境的内场仿真。

2) 不需要掌握目标和天线的几何模型信息,即可开展计算。

3) 方法的计算效率对求解频率、场景电尺寸不敏感,在同样的仿真计算机配置下,相较其他方法具备更好的电大复杂场景的电磁环境仿真预测能力。

未来将开展进一步的研究,使本文方法可以处理近场辐射源与散射体耦合的情况。