旋转部件SGBEM-FEM 耦合热弹性断裂分析
2022-10-13董雷霆贺双新
董雷霆 贺双新
(北京航空航天大学 航空科学与工程学院, 北京 100083)
Abstract: Rotational components undergo complex loads which can easily initiate cracks, resulting in fatigue and fracture failures. For thermal-loaded rotational components with cracks, the finite element method(FEM) was applied to the global structure without cracks, thus exerting the advantage of FEM in numerical analysis of large-scale structure; meanwhile, the symmetric Galerkin boundary element method (SGBEM) was employed to the subdomain around the crack, thereby developing the advantage of SGBEM in fracture analysis. The SGBEM super element, which took the influence of the rotational inertia loading and the thermal loading into consideration, was developed in this paper. The stiffness matrix of the obtained SGBEM super element was symmetric and positive semidefinite, where the rotational inertia loading and the thermal loading only influence the equivalent force vector. Thus, the SGBEM super element can be directly assembled with the stiffness matrix and the equivalent force vector of the FEM, and be coupled with the FEM to solve the thermoelastic fracture problem of rotational components. Stress intensity factors of the cracked rotational disk undergoing the thermal loading were computed, which validates the effectiveness of SGBEM super element and FEM coupling method.
Keywords: symmetric Galerkin boundary element method (SGBEM); super element; thermoelasticity;rotational inertia load; stress intensity factor
涡轮盘和转子叶片等旋转部件的疲劳断裂是航空发动机的常见多发故障[1-3],严重影响航空发动机和飞机的安全性与可靠性。 旋转部件的高效仿真分析,特别是应力强度因子等断裂参数的精确快速计算,对飞机和航空发动机的结构仿真分析和结构完整性评估具有重要意义[4-5]。
有限元法(finite element method,FEM)[6]广泛应用于大型复杂结构的仿真分析,已成为当今工程技术领域应用最为广泛、成效最为显著的数值分析方法。 FEM 采用连续函数作为形函数,然而在裂纹几何面处的位移场具有不连续性,并且在裂纹尖端处的应力场具有奇异性[7],因此FEM在处理裂纹这种强不连续问题方面具有难度,需要在裂纹尖端的高应力区划分致密的网格[8],这增加了问题求解规模,且限制了断裂力学参数的求解精度。
对称伽辽金边界单元法(symmetric Galerkin boundary element method,SGBEM)[9-10]在结构断裂仿真分析方面具有优势。 对于三维断裂力学问题,由于SGBEM 无需内部网格,仅在裂纹面划分网格,相比有限元,大大降低了裂纹尖端应力集中区域网格划分难度;其面力边界积分方程中的检验函数选取为位移场[11],可以精确计算裂纹张开位移,配以裂尖1/4 结点单元后[12],SGBEM 可得到很高的应力强度因子计算精度[13];并且SGBEM 的位移和面力边界积分方程是弱奇异的[14],这降低了数值积分计算难度。 但由于SGBEM 的系数矩阵是满阵[15],随着自由度数目的增加,会导致计算规模快速增加,因此难以用于求解复杂结构。
SGBEM 超单元FEM 耦合法[16]结合了FEM求解大型复杂结构的优势和SGBEM 求解断裂问题的优势。 该方法在裂纹附近局部子域使用SGBEM 求解,构造了SGBEM 超单元;在全局无裂纹区域使用FEM 求解;由于SGBEM超单元对称且半正定,可直接装配至全局有限元的刚度矩阵中,从而耦合求解含裂纹的复杂结构。 该方法对飞机二维结构如加筋板裂纹黏结修复、耳片接头裂纹疲劳失效等实际问题可进行高效的仿真分析。 但该方法没有考虑旋转惯性载荷和热载荷对含裂纹局部子域产生的影响,不能直接用于三维旋转部件的热弹性断裂分析。
本文将SGBEM 超单元FEM 耦合法推广至三维旋转部件的热弹性断裂问题。 推导了三维情况下考虑热载荷和旋转惯性载荷的SGBEM 超单元,将SGBEM 超单元应用于含裂纹局部子域,并给出SGBEM 超单元FEM 耦合的过程,计算算例验证了该方法。
1 旋转部件热弹性SGBEM 超单元
1.1 位移和面力边界积分方程
如图1 所示,设弹性体Ω内存在体力f和温度场T,源点ξ和场点x均位于弹性体Ω的边界∂Ω上。 伽辽金式位移边界积分方程[17-18]为

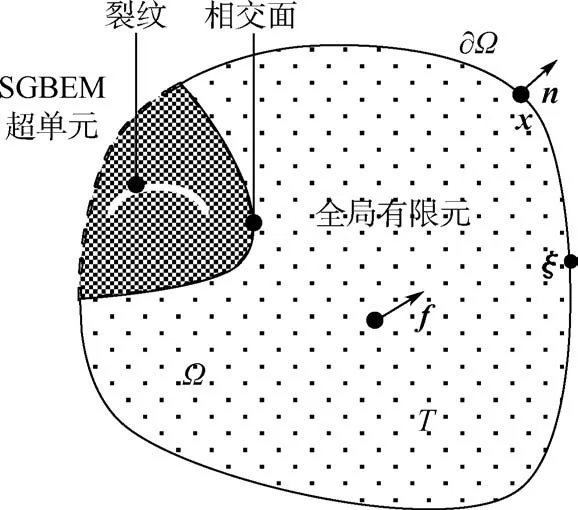
图1 热弹性体Fig.1 Thermoelastic body

伽辽金式位移边界积分方程式(1)是将传统边界元法中的位移边界积分方程写为弱形式,并对核函数使用亥姆霍兹(Helmholtz)分解进行弱奇异化后得到的;伽辽金式面力边界积分方程式(2)是将强奇异的应力边界积分方程写为弱形式,并对核函数使用亥姆霍兹分解进行弱奇异化后得到的。 将伽辽金式位移和面力边界积分方程在边界网格上离散,再求解相应的线性方程组即可得到边界上的位移和面力,从而可以求解裂纹的张开位移,并使用位移外推法获得裂纹应力强度因子。
1.2 SGBEM 超单元构造格式
将伽辽金式位移边界积分方程式(1)和伽辽金式面力边界积分方程式(2)离散。 为简化推导过程,本文不列出一个边界单元系数矩阵组装到对称伽辽金边界单元法中系数矩阵的过程。 不失一般性,假设边界上位移和面力均为未知的。
边界上位移可离散为



1.3 含裂纹SGBEM 超单元

添加此约束条件后,无需将2 个裂纹面分别划分网格,仅需在一个裂纹面划分网格即可,可直接计算裂纹面张开位移。
式(13)代入SGBEM 超单元的构造格式(9),即得含裂纹弹性体的SGBEM 超单元构造格式。
2 SGBEM 超单元FEM 耦合法
2.1 SGBEM 超单元FEM 耦合构造格式
如图1 所示,局部子域和全局有限元区域相交面上有重合的面单元和重合的结点。
位移有限元的表达格式可写为

分别装配式(14)、式(15)的刚度矩阵和等效结点力向量,可得SGBEM 超单元FEM 耦合构造格式:
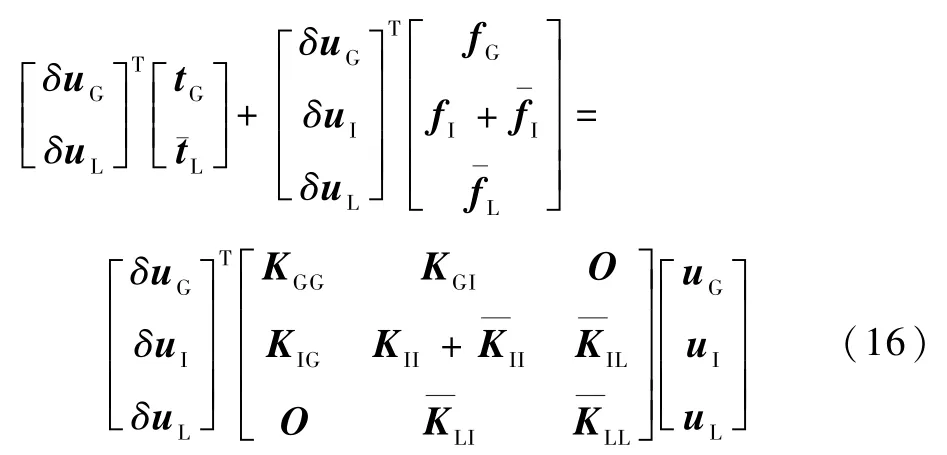
注意到,有限元区域与局部子域相交面上存在着相交结点,有限元在相交结点上的面力tI与SGBEM 超单元在相交结点上的面力¯tI大小相等,方向相反,即tI=- ¯tI,故式(16)不显示相交结点上的面力。
2.2 SGBEM 超单元FEM 耦合求解流程
SGBEM 超单元FEM 耦合求解流程采用自动化的软件完成,用户仅需要独立划分有限元网格与裂纹面网格。 如图2 所示,详细耦合求解过程如下。
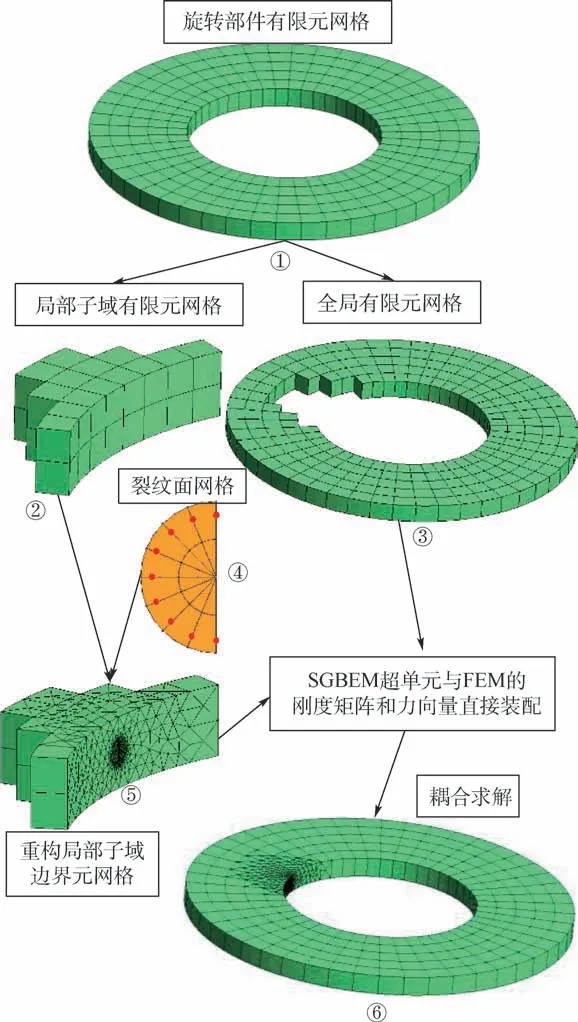
图2 SGBEM 超单元FEM 耦合求解流程Fig.2 Process of SGBEM super element and FEM coupling solution
1) 搜索局部子域。 当旋转部件划分好有限元网格后,根据旋转部件中裂纹位置,找到裂纹附近有限元单元,这些有限元单元构成了局部子域有限元网格。
2) 消除内部结点。 注意到,裂纹面网格是另外插入的,裂纹面网格结点与局部子域有限元网格结点没有任何关系。 对于内部裂纹,需要将局部子域有限元网格中内部结点消去,仅保留边界面单元,这些边界面单元和裂纹面单元共同构成了局部子域边界网格,如图3 所示,为清楚显示内部,该图隐藏了部分边界单元。
3) 重构局部子域。 对于面裂纹,以图2 中④所示半圆形裂纹为例,其在局部子域中的位置如图3所示。 裂纹前沿(即半圆曲线)上的结点在局部子域内部,无需处理;但该裂纹的开口线(即半圆直径线)上的结点既在裂纹面上,也在局部子域边界面上。 因此,需要重新划分局部子域边界面(见图2 中⑤部分)。 注意,局部子域和全局有限元相交面上的边界面单元不可以重构,因为相交面上的结点是局部子域和全局有限元共有的。
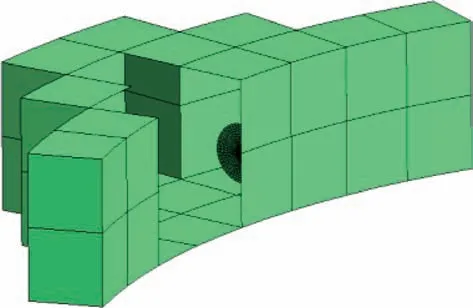
图3 局部子域边界网格和裂纹网格Fig.3 Subdomain boundary mesh and crack mesh
4) 装配刚度矩阵。 在获得局部子域边界元网格后,分别求解局部子域SGBEM 超单元和全局有限元,获取SGBEM 超单元的刚度矩阵和有限元的刚度矩阵,再通过结点编号直接装配。
5) 施加载荷。 根据式(9)等号左端第2 项求解局部子域旋转惯性载荷和热载荷产生的等效载荷列向量,并求解全局有限元中的载荷列向量。再按照式(16)等号左端第3 项将局部子域等效载荷列向量装配至全局有限元中的等效载荷列向量。
6) 耦合求解。 步骤4)和步骤5)给出局部子域SGBEM 超单元和全局有限元的刚度矩阵和等效载荷列向量的整体装配形式。 求解该线性方程组,可获得局部子域SGBEM 超单元和全局有限元所有结点的位移解,包括裂纹张开位移,从而可以使用位移外推法求解裂纹应力强度因子。
3 含裂纹受热旋转圆盘算例
本节使用SGBEM 超单元FEM 耦合法求解图2中的受热旋转圆盘,以展示其优点。
如图4 所示,圆盘内径Ri=0.1 m,外径Ro=0.2 m,厚t=0.02 m,弹性模量E=1 000 MPa,泊松比ν=0.3,线膨胀系数α=2.17 ×10-5/℃。 绕圆盘中心轴的转速为ω,转速ω的取值如表1 所示。 沿径向的温度分布为
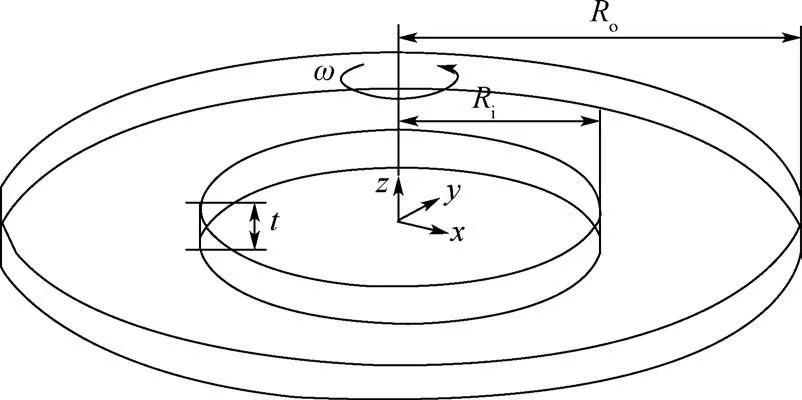
图4 受热旋转圆盘Fig.4 Rotational disk undergoing thermal loading

式中:系数k的取值如表1。 在圆盘内环面中间存在一半圆形面裂纹,半径为r= 0. 004 m(见图3);在圆盘内环面中心处施加刚体位移约束。
该圆盘的SGBEM 超单元FEM 耦合法求解流程见2.2 节。 分别使用SGBEM 超单元FEM 耦合法和商业有限元软件ANSYS Workbench 计算半圆形裂纹圆弧中点处的I 型裂纹应力强度因子。 ANSYS Workbench 所使用的有限元网格见(见图5(a)),该网格比图2 中⑥部分的耦合法所用的网格更加密集;且ANSYS Workbench 在裂纹附近使用了多种体单元,有五面体棱柱单元、六面体单元、五面体金字塔单元以及四面体单元(见图5(b))。 可见,耦合方法使用了更加稀疏的网格,在裂纹尖端处仅使用了四边形单元,网格也更加简单(见图2 中④部分)。
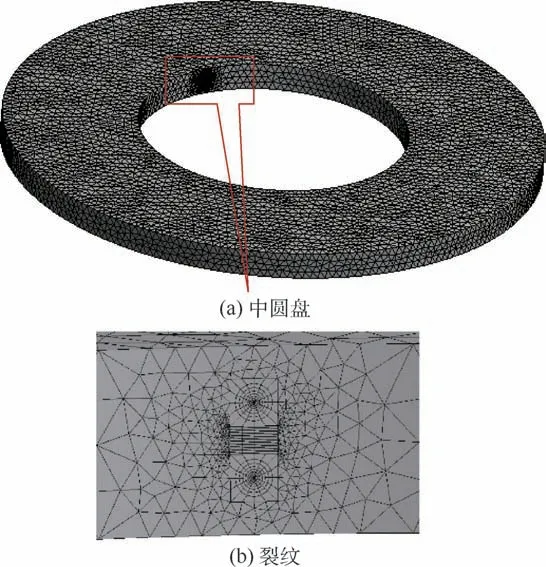
图5 ANSYS Workbench 中圆盘和裂纹的有限元网格Fig.5 Disk and crack FEM mesh used by ANSYS Workbench
受热旋转圆盘I 型裂纹应力强度因子计算结果如表1 所示,不同转速和温度下,SGBEM 超单元FEM 耦合法与ANSYS Workbench 的计算结果相比,误差均小于2%,可见SGBEM 超单元FEM耦合法可有效用于旋转部件的热弹性断裂分析。
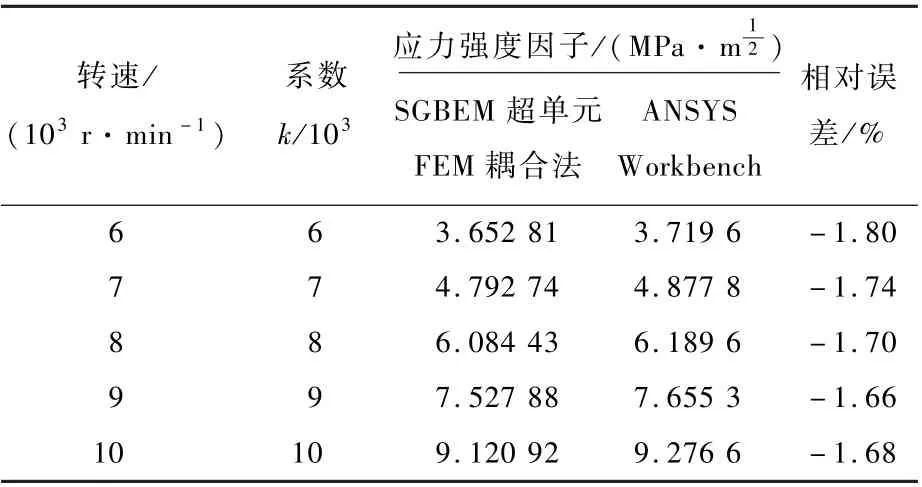
表1 不同转速和温度下圆盘裂纹应力强度因子Table 1 Stress intensity factors of crack in disk for different rotational speeds and temperature
该算例中本文方法在不含裂纹的全局区域进行稀疏的有限元剖分;在裂纹附近仅使用二维单元进行边界元的计算,仅需要对裂纹面和包络裂纹的局部子域表面进行简单的二维网格划分,避免了裂纹附近细致的三维有限元网格剖分,可以显著减少单元数量。 关于SGBEM-FEM 法模拟断裂与疲劳问题的在网格剖分和计算效率方面的优势,请见文献[19-20]中给出的详细论述。
4 结 论
本文给出了三维旋转部件SGBEM 超单元的具体构造格式。 本文将SGBEM 超单元与有限元耦合,计算了旋转圆盘在热载荷作用下半圆形裂纹的应力强度因子,并与商业有限元软件ANSYS Workbench 结果进行对比,对比结果表明了该SGBEM 超单元FEM 耦合法可有效用于旋转部件的热弹性断裂分析。 通过SGBEM 超单元FEM 耦合求解流程可知:
1) 有限元网格独立划分,不受裂纹干扰。 由于裂纹面不使用有限元单元,有限元网格可自由按需划分,无需考虑裂纹尖端应力集中区有限元网格加密的困难。
2) 裂纹面网格独立划分,难度降低。 裂纹仅使用边界单元,可自由按需划分,且内部裂纹无需重构网格。 虽然面裂纹存在网格重构问题,但仅需在局部子域边界曲面上划分二维网格,相比传统有限元需在裂纹附近区域划分致密的三维网格,难度大大降低。
3) 耦合过程简单。 由于SGBEM 超单元仅存在位移自由度,不存在面力自由度,从SGBEM 超单元FEM 耦合构造格式可知,其与有限元的装配耦合过程与有限元中一个单元的刚度矩阵装配至整体刚度矩阵的过程完全一致。
4) 裂纹尖端网格简单。 SGBEM 超单元FEM,耦合法在裂纹前沿使用1/4 结点面单元。而有限元需要使用多种形状的体单元划分不规则形状的裂纹前沿。
5) 有助于快速仿真裂纹扩展。 当进行裂纹扩展仿真时,每当裂纹扩展一段距离,对于内部裂纹,耦合方法仅需在裂纹前沿增加一层边界面单元即可继续仿真;对于面裂纹,仅需再次重构局部子域裂纹附近处的边界面网格。 但对有限元而言,需要重新划分裂纹附近区域体单元网格。
附录A:

附录B:
当弹性体作用有旋转惯性载荷时,如果使用散度定理将旋转惯性载荷引起的域积分转换为边界积分,则伽辽金式位移和面力边界积分方程式(1)和式(2)中关于旋转惯性载荷的函数为

