变频环境下异步电机故障诊断方法

2022-10-13黄向慧田坤臣荣相魏礼鹏杨方

机床与液压 2022年18期

黄向慧，田坤臣，荣相，魏礼鹏，杨方

(1.西安科技大学电气与控制工程学院，陕西西安 710000；2.中煤科工集团常州研究院有限公司，江苏常州 213000；3.天地(常州)自动化股份有限公司，江苏常州 213000 )

0 前言

异步电机具有结构简单、安全可靠和生产成本低等优点，是目前工业生产、运输和电力系统广泛使用的一种电机。大中型异步电机多采用鼠笼型转子，一旦发生故障，将会导致整个系统停止工作，如果可以在故障初期尽早预警，就可以减少因电机故障带来的经济损失。在异步电机的各种故障形式中，最常见的是转子断条故障和偏心故障。随着变频器的发展，越来越多的电机是在变频环境下运行的，若在变频环境下能够对这些故障进行较为准确的诊断，对于异步电机的稳定运行有着极为重要的意义。

在变频环境下原始信号不但会受到大量的噪声干扰，还会由于高频功率电子器件所产生的高频脉冲在电机的定子线圈内产生谐波干扰，需要对信号进行特征提取。苏建芳、吴钦木利用小波包对故障信号进行分析，依据各类故障特征频率，对信号进行小波包分解和重构，得到相应的故障特征，但是如果信号是非平稳信号，在选取小波基函数上会存在一定困难；谭勇、刘振兴提出一种基于分数阶Fourier和频域Relax算法进行故障提取的方法，将线调频变化的电流主分量转换成恒频分量，再通过频域Relax方法提取和剔除该恒频成分，突出故障特征，但是会存在对各个频率分量的参数估计不准确的问题；张建文等提出利用扩展Park矢量的方法，将故障特征频率分量从原始电流信号中剥离出来，减少基频信号的影响，采用频谱方式使之得到突显，但是高频成分会对处于低频段的故障特征频率造成一定干扰；刘美容等提出采用EMD方法进行故障特征提取，将非平稳信号拆成频率从高到低排序的多个频段的本征模式函数，但是该方法存在很严重的模态混淆情况。在故障识别方面，李卫民等搭建支持向量机分类模型，近似熵特征量被划分为训练样本和测试样本，该方法只适合小样本集；马天兵等采用BP神经网络，选取不同样本对神经网络进行测试，容易出现局部最小化问题；鞠晨等人通过粒子群优化算法优化BP神经网络的初始权值和阈值，可以避免陷入局部极小值；李思琦、蒋志坚先进行EEMD分解，再计算信号陡峭度及其他一系列指标后使用卷积神经网络进行故障诊断。

本文作者针对变频环境下异步电机断条和偏心故障提取方法，提出了互补集合经验模态分解(Complementary Ensemble Empirical Mode Decomposition，CEEMD)，使用排列熵和样本熵作为判断有效IMF信号的依据，将选择出来的IMF信号重构，多组重构后的数据组成数据集，通过一维卷积神经网络进行训练分类诊断，并保存最优训练模型，通过实例信号进行验证，结果表明提出的方法可以实现故障诊断。

1 CEEMD-CNN算法理论

1.1 CEEMD算法理论基础

互补集合经验模态分解(CEEMD)是模态经验分解(EEMD)改进的一种方法。EEMD是在被分解信号中加入高斯白噪声，相较于传统EMD可以较好地抑制模态混淆情况，但是在分解过程中高斯白噪声会影响分解出来的IMF信号，导致分解出来的IMF信号准确性不高。互补集合经验分解则是通过添加一对相位相反、幅值相同的高斯白噪声来进行分解，不仅可以进一步抑制模态混淆情况，还可以减少因添加高斯白噪声造成的重构信号误差。CEEMD的具体分解步骤与EEMD分解大致一样，EEMD分解方法详细参照文献[12]。CEEMD具体步骤如下：

(1)在初始信号()中加入一对相位相反、幅值相同的高斯白噪声构成两个新的信号()和()，其中

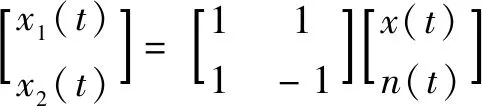
(1)

式中：()为添加的高斯白噪声。

(2)对()和()进行三次样条插值拟合得到上包络线和下包络线，并取平均值记为()和();

(3)用()和()分别减去平均值()和()，得到新的数据序列()和()，若()和()满足本征模态函数则作为一个IMF分量，不满足则对以上步骤进行重复操作，直到符合本征模态函数;

(4)将第一个IMF分量从()和()中进行分离，得到新的分量，以此类推循环多次，直到不能再提取出满足条件的分量后停止循环，再将()和()得到的两组IMF信号两两对应求平均值，得到最终IMF分量。

1.2 样本熵原理

样本熵可以比较出各IMF信号的复杂程度，计算得到的样本熵越大，则该信号复杂性越高，反之复杂性越低。样本熵计算步骤如下所示：

(1)假设实际信号为()，嵌入维数=2，相似容限=01×[()]，其中[()]是数据信号的标准差，参照实际信号对其重构，重构一个维向量。

()={,+1,…，+-1}，1≤≤-+1

(2)

(2)定义为()和()对应元素之差绝对值最大值的距离，统计<的个数(<)，定义()为

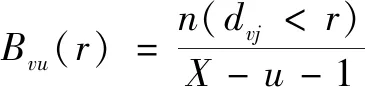
(3)

(3)对()求平均值()，再对维数+1重复以上几步得到+1()和+1()。

(4)得到样本熵的表达式为

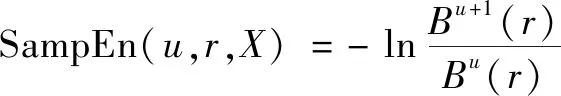
(4)

样本熵具有比时域统计更好的估计效果，对原始数据处理时无需进行粗粒化提取，且抗干扰能力强，是常用的一种熵值计算方法。本文作者选择小于平均值的IMF信号为有效信号。

1.3 排列熵原理

排列熵是一种用于描述信号复杂程度的非线性估计方法，排列熵值越大，则说明该信号的时间序列越复杂，反之信号就越简单。排列熵计算步骤如下所示：

(1)假设数据是长度为的时间序列，将此序列按照相空间延迟坐标法进行重构，若该序列中每一个采样点都选取连续的个样本点，就可以得到()的维重构向量：

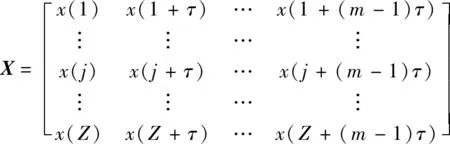
(5)

其中：为嵌入维数，这里取=5；为延迟时间，这里取=1。

(2)上述矩阵每一行都可看做一个重构分量，将矩阵第行按升序的方式排序，都将得到一组位置索引序列,记为()，它是符号序列的其中一种：

()=(，，…，),=1,2,3,…，

(6)

式(6)中≤!。符号序列出现的概率记为(=1，2，…，)，它满足:

(7)

(3)序列{(),=1,2,…,}的排列熵可以定义为

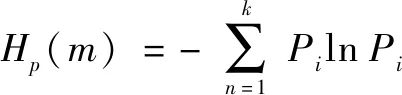
(8)

(4)对排列熵进行归一化处理可得：

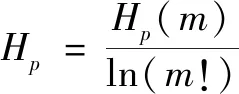
(9)

排列熵能够有效放大时间序列的微弱变化，且计算简单、实时性好。这里同样选择小于平均值的IMF信号为有效信号。

1.4 卷积神经网络(CNN)

卷积神经网络是一种具有代表性的深度学习算法，其主要结构通常由卷积层、池化层以及全连接层3个部分组成。卷积层是卷积神经网络的核心，提取输入数据中包含的特征；池化层用于实现对特征图的降采样操作；最后通过全连接层对得到的特征图进行铺展和连接，通过采用ReLU函数作为激活函数的隐藏层，结合softmax函数实现分类结果的输出。

其中卷积操作的原理如图1所示。

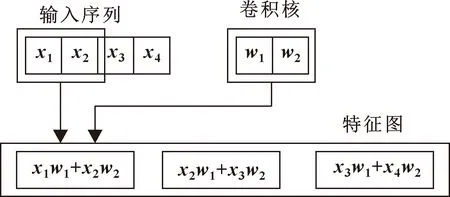
图1 卷积操作原理

不难发现，图1中输入序列的数据维度为4，卷积核的维度为2，卷积后输出的数据维度为3，存在数据维度减少的问题。为了保持信号的维度不发生变化，可以采取补零策略，即在输入序列最前面或最后面补零，可以保证输出维度不变。

2 故障诊断步骤

变频环境下异步电机故障诊断步骤主要分为四部分：数据样本的获取、故障特征的提取、仿真数据故障类型的识别以及实测数据故障类型的识别，电机故障诊断流程如图2所示。

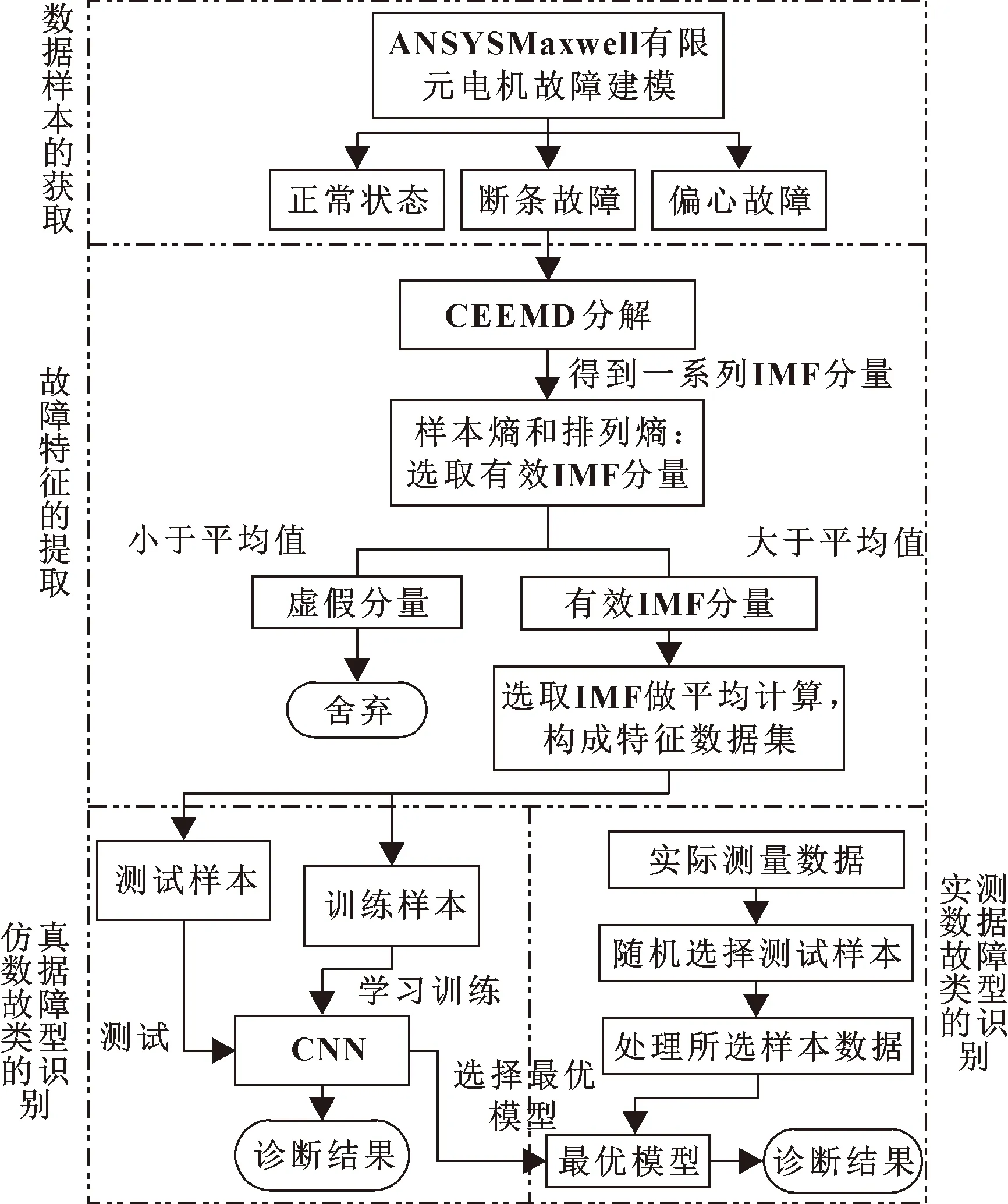
图2 电机故障诊断流程

具体步骤如下：

(1)基于ANSYS软件分别对正常电机、转子断条电机、气隙偏心电机建模并进行有限元分析，在Simplorer中搭建一个SPWM电路联合仿真，获取仿真定子电流数据。

(2)对获取的电流数据进行滤波处理和CEEMD分解，可得到多个IMF信号。

(3)计算每个IMF信号的样本熵和排列熵，选择低于平均值的IMF信号为有效信号。

(4)将选择的IMF信号进行重构，将多组重构信号组成数据集，作为卷积神经网络的样本集。

(5)设计CNN结构和基本参数，将定子电流数据集划分为训练集与验证集，分别对CNN模型进行训练与验证，最终得出故障诊断结果并保存训练效果最好的模型。

(6)通过搭建实验平台，分别对正常电机、断条电机以及偏心电机3种状态收集电流信号，再重复步骤(2)—(3)，将得到的电流信号数据集放到步骤(5)训练好的模型中进行故障诊断。

3 仿真验证

通过设置SPWM电路中正弦调制波频率为40、50、60 Hz，从而达到输出频率也为40、50、60 Hz的效果，再由SPWM电路与三相异步电机模型进行联合仿真，收集不同状态的电流信号。

3.1 Maxwell有限元建模

在Maxwell搭建一个三相异步电机，对电机的有限元模型进行参数设计，在RMxprt中可以自动生成电机模型。此次搭建的是一个型号为380V YB3-160M的三相异步电机，采用星形接法，电机模型如图3所示，电机参数如表1所示。

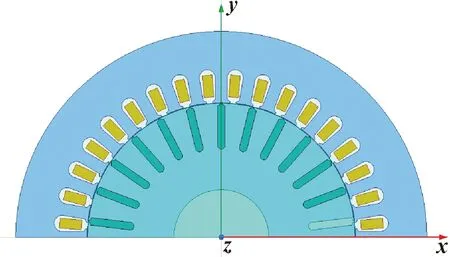
图3 三相异步电机模型

表1 YB3-160M-4型电机参数

断条故障一般指的是电机导条和端环断裂，通过改变鼠笼导条铸铝材料参数将电导率调至2 S/m，远低于其他导条电导率，即可达到转子断条故障的效果。偏心故障通过改变定子、转子、铁芯位置及坐标系可获得气隙偏心故障，再通过建立相对坐标系区分静态偏心和动态偏心，通过文中的研究，可以将静态偏心和动态偏心划分为一类偏心故障进行故障诊断，这里统一设置偏心度为20%。

3.2 Simplorer外电路

变频环境通过搭建一个基于正弦脉宽调制(SPWM)技术变频电路来实现，通过控制逆变电路中开关器件的通断，使电路输出一系列幅值相等宽度不等的脉冲波，用脉冲波来代替正弦波。通过改变载波与调制波的频率比可以改变输出电压的频率，实现变频输出，如图4所示。

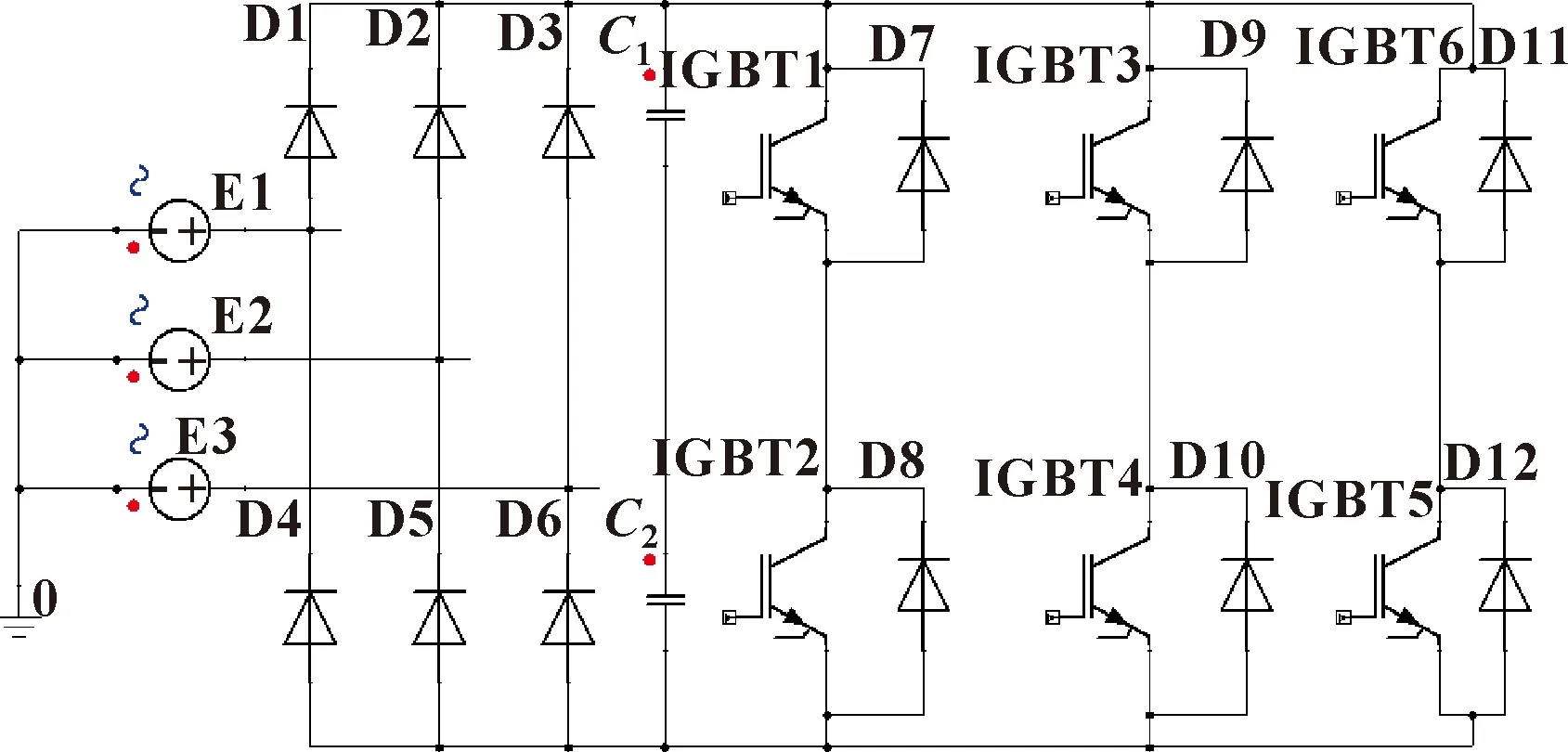
图4 变频电路

3.3 基于CEEMD的故障特征提取

以断条故障电机电流信号数据为例进行CEEMD分解，分为10个IMF分量和1个残余分量，残余分量这里不做考虑，如图5所示。

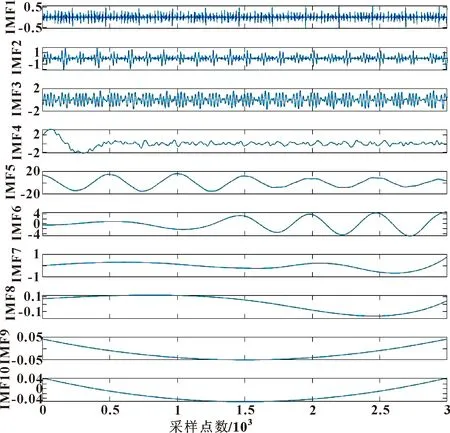
图5 CEEMD分解结果

对CEEMD分解后的各IMF信号分别进行样本熵和排列熵的计算，选取低于熵值平均值的IMF信号，选取结果见表2和表3。

表2 CEEMD分解后样本熵选取IMF结果

表3 CEEMD分解后排列熵选取IMF结果

为方便后面使用卷积神经网络进行故障诊断，这里统一对样本熵选取结果选择IMF5～IMF10作为有效IMF信号，对于排列熵选取结果选定IMF4～IMF10作为有效IMF信号。

将选定的IMF信号做一个平均值的计算，使其得到一个重构后的数据，再由多组数据组合成一个数据集，将该数据集放入卷积神经网络中进行训练，为保证每组数据集含特征，文中使用的数据集共13 500条数据(3种频率平均分配)，每条包含3 000个点。

3.4 基于CNN的故障类型识别

3.4.1 CNN的建立

使用的卷积神经网络的参数如表4所示。使用Adam优化器优化模型，设Dropout为0.3，学习率为0.000 1。从数据集中各随机选出70%数据作为训练集，共9 450条数据，剩下30%的数据作为验证集，共4 050条数据。每次从训练集选择32条数据进行训练，最后使用训练好的卷积神经网络模型对验证集进行验证，检验模型的可用性。

表4 卷积神经网络的参数

3.4.2 CNN诊断结果

为了验证文中所述故障诊断方法能够有效地提高在故障识别过程中的精度，采取多种方法进行对比，其中为通过排列熵选取的IMF信号进行重构得到的数据集，为通过样本熵选取的IMF信号进行重构得到的数据集，实验结果如表5所示。

表5 实验结果

图6为使用数据集CEEMD-CNN方法训练得到的训练集和验证集的准确率的变化情况，图7为损失函数变化情况。

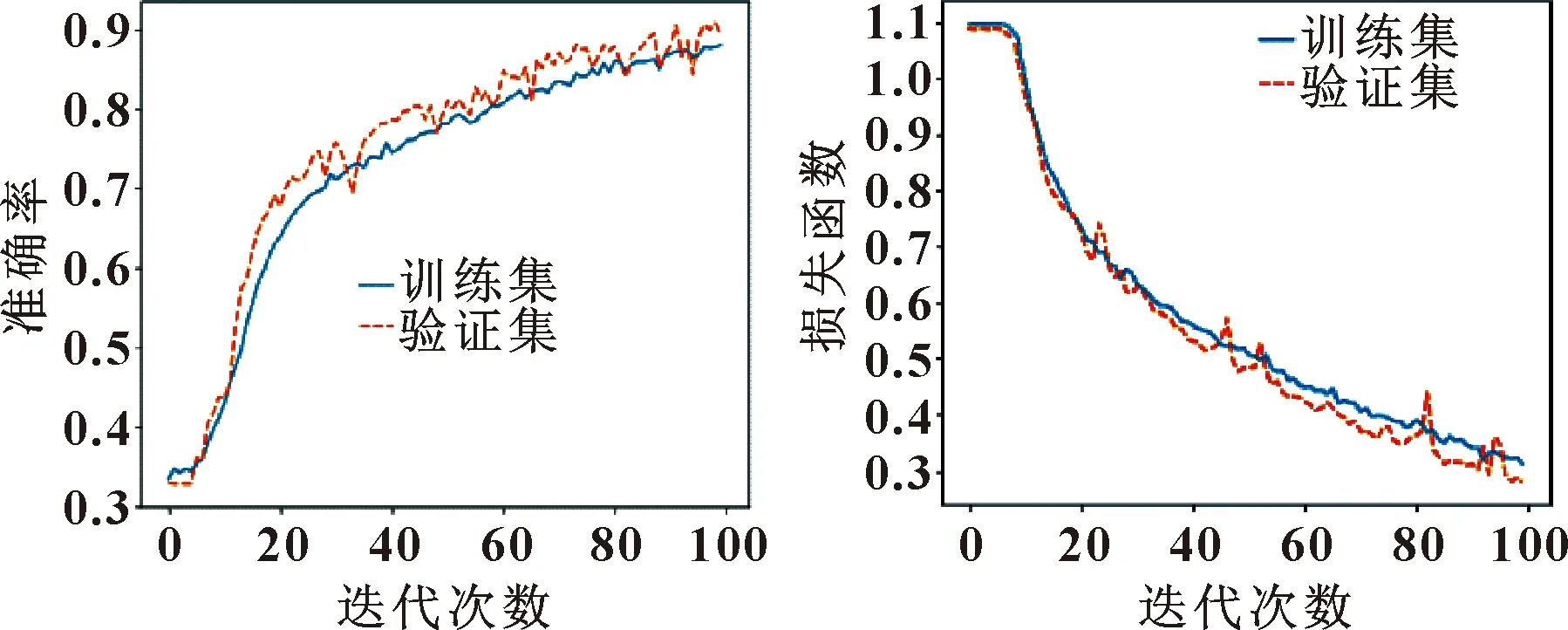
图6 准确率变化情况(未滤波) 图7 损失函数变化情况(未滤波)

由上述结果可知：这样进行故障诊断的准确性并不高，这是因为变频环境下故障特征易受基频影响，会引起较大误差，如果直接对原始信号进行处理，工频信号和谐波信号会产生干扰，得到的效果并不理想。因此本文作者对原始信号进行滤波处理，去掉基频，实验结果如表6所示，对比滤波之后的结果可见，对信号进行滤波处理是很有必要的。

表6 滤波之后实验结果

图8为滤波之后使用数据集CEEMD-CNN方法训练得到的训练集和验证集准确率的变化情况，图9为损失函数变化情况。

图8 准确率变化情况(滤波后) 图9 损失函数变化情况(滤波后)

由上述结果可知：对原始信号进行滤波处理至关重要，使用EEMD和CEEMD提取故障特征存在差异性，同样的方法使用排列熵选出来的重构数据集比样本熵选出来的准确率高。这是因为样本熵在处理大量数据的时候，计算效率较低，因此使用排列熵作为选择IMF信号的CEEMD-CNN方法具有更好的故障诊断效果。

4 实验平台验证

实验平台如图10所示，主要包括5个部分:三相异步电机，变频器，控制台，扭矩传感器和电涡流制动器，其中扭矩传感器用来测量电机的转速和扭矩，电涡流制动器用来给电机加负载。通过给转子钻一个5 mm的孔达到断条故障效果,如图11所示;这里通过移动轴承端盖扩大0.15 mm达到偏心度为20% 的效果，如图12所示，通过控制台中电流传感器收集电流信号，再对信号进行滤波处理和CEEMD分解，随机取90组数据(断条电机，偏心电机和正常电机各取30组数据)，其中40、50、60 Hz各占1/3组成测试集进行测试，编号0为电机正常状态，编号1为电机断条故障，编号2为电机偏心故障，得到的混淆矩阵如图13所示，验证结果如表7所示,总识别率为95.56%。