机床空间精度预测与NC代码补偿研究
2022-10-13陈廷兵敬正彪李志强
陈廷兵,敬正彪,李志强
(1.成都工业学院智能制造学院,四川成都 611730;2.成都工业职业技术学院装备制造学院,四川成都 610218)
0 前言
在机床加工空间内,实际刀尖相对工件切削位置发生的偏离即为机床空间偏差。在机床各项几何误差综合影响下,空间精度的局限性严重制约着机床加工精度。因此,搭建精确数控机床空间精度模型是提升机床空间精度补偿的前提条件,而机床空间精度补偿是提高机床加工精度的重要技术手段,可为数字制造精度补偿技术提供参考。
国内外学者针对机床空间精度建模展开了众多研究,XIANG等提出了一种多机床空间精度广义模型,利用广义模型和分布式误差补偿技术,建立了详细的三轴和五轴机床广义运动学模型;YUEN 和ALTINTAS提出了一种补偿六自由度旋转磁台集成的三轴龙门式微机床几何误差引起的刀具位置误差的方法,利用齐次变换矩阵建立了九轴机床的无几何误差理想正运动学模型。
针对机床空间精度补偿,HSU 和WANG提出了一种新的五轴机床几何误差补偿方法——解耦法,该方法建立在只考虑机床旋转轴运动的刀具定位误差模型的基础上,与传统的同时计算旋转轴和直线轴误差补偿的方法相比,进一步分别计算了旋转轴和直线轴的误差补偿;ZHU等通过逆向修正相应的数控代码对识别出的几何误差进行补偿,为了验证该方法的有效性,开发了一个原型软件系统,可用于任意类型的五轴以上数控机床的实验。
综上所述,传统机床空间精度建模与补偿存在以下问题:难以实现完整机床空间精度的建立,间接导致补偿结果不理想;存在补偿残差的问题。针对上述问题,以某立式加工中心为研究载体,基于旋量理论建立机床空间精度模型。在此基础上,输出空间精度预测图,进而针对传统空间精度补偿不充分的局限性,将空间精度补偿思路转换为NC代码最优化问题;基于遗传算法求解该最优化问题,通过实验验证优化结果的有效性。
1 机床空间精度建模
1.1 机床几何误差
图1为立式加工中心结构示意图。一般地,三轴立式加工中心有、、轴,每个轴共6项几何误差,3根直线轴共计18项几何误差,同时包含3项垂直度。因此,三轴立式加工中心共计21项几何误差,后续机床空间精度建模应保证包含全部21项几何误差。几何误差如表1所示,几何误差原理如图2所示。
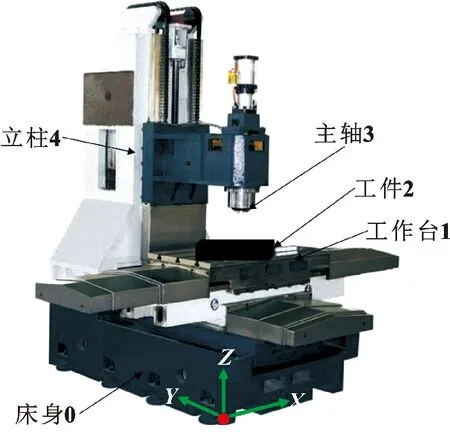
图1 立式加工中心示意

表1 21项几何误差

图2 几何误差原理
1.2 机床运动链
将该立式加工中心运动链划分为机床刀具运动链和机床工件运动链,其中刀具坐标系和工件坐标系分别为{W}、{T},其原点分别为W、T;机床参考坐标系为{C},其原点为C,如图3所示。

图3 机床运动链简图
充分考虑刀具与工件在机床坐标系下的位置是实现机床空间精度完整建模的重要前提。刀具和工件坐标系在机床坐标系下的位置坐标分别为
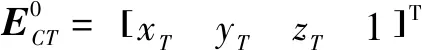
(1)

(2)
式中:、、分别为刀尖点在机床坐标系下各轴分量;、、分别为工件切削点在机床坐标系下各轴分量。此处仅给出了机床坐标系的刀具与工件空间位置,并未给出姿态矩阵。由于三轴无法实现姿态输出,因此式(1)(2)矩阵为4×1形式。
1.3 机床空间精度建模
机床空间误差是由于几何误差综合作用下导致机床刀尖点偏离了工件切削点,因此应该输出理想状态与实际状态下机床2条运动链(刀具链和工件链)的运动学正解模型。
理想状态下(几何误差未参与),基于旋量理论可得出刀具运动链与工件运动链末端运动矩阵为

(3)

(4)
式中:为刀尖点在机床坐标系下的理想运动矩阵;为工件在机床坐标系下的理想运动矩阵。
实际状态下(有几何误差参与),机床进给过程中存在几何误差,则实际刀具链与工件链运动矩阵为


(5)

(6)


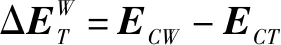
(7)
根据大量文献得到,传统的基于D-H构建的机床空间精度模型与基于旋量理论搭建的机床空间精度模型存在部分差异,差异性主要体现在运动学矩阵与误差矩阵相乘存在“左乘”与“右乘”的差异。由于D-H理论在建立机床各运动部件局部坐标系后,在局部坐标系作齐次坐标系转换时相对前一个运动部件的坐标系参考,必须选用右乘原则;而基于旋量理论的机床空间精度建模时,所有运动部件均以机床坐标系为唯一固定参考坐标系,必须选用左乘原则,同时旋量理论建模的最大优势在于仅需建立唯一机床坐标系即可满足机床空间精度建模的需求。
基于机床空间精度基本定义,推导计算该立式加工中心空间精度模型Δ为

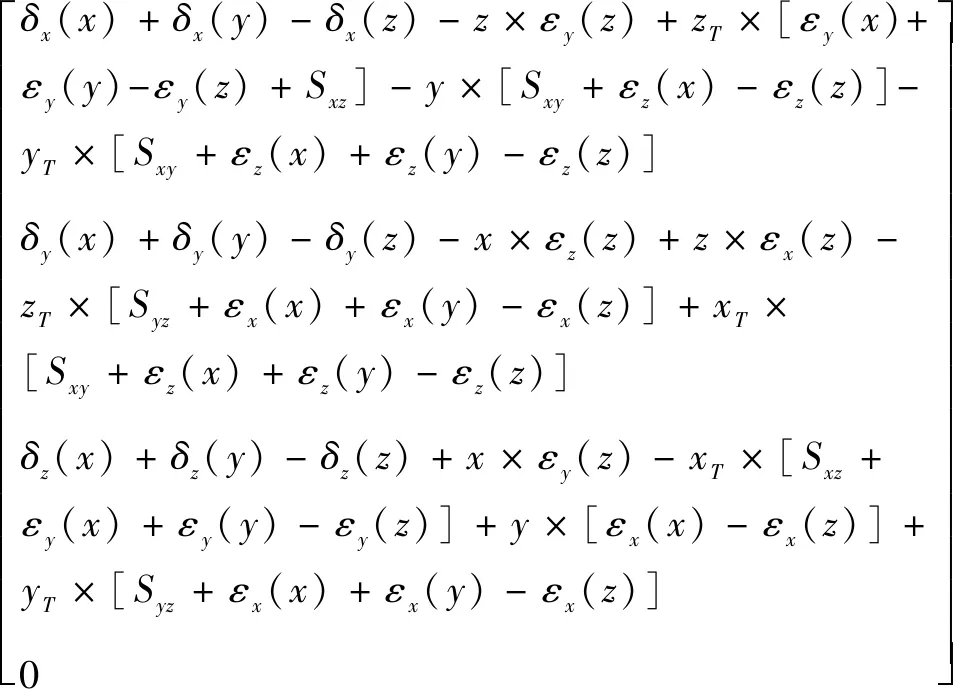
(8)
式中:、、分别为工作空间内各轴进给行程;Δ、Δ、Δ分别为各轴空间精度投影。
综上所述,基于旋量理论建立了该立式加工中心空间精度模型,可以看出,该空间精度模型包含了全部21项几何误差,保证了所建空间精度模型的完整性,为后续机床空间精度补偿提供了可靠的数学模型。
2 空间精度预测
上述参数模型无法直观表述该机床空间精度分布情况,因此,借助九线法辨识各项几何误差后代入式(8)中,规划该机床加工空间运动范围为400 mm×400 mm×400 mm,从而输出该机床加工空间内空间精度分布预测结果,如图4所示。
图4中红色部分代表该空间精度较差,橙色部分空间精度较好。预测图不仅可以输出任意空间位置空间精度,同时为后续空间精度补偿提供了方向。

图4 空间误差预测图
3 机床空间精度补偿
3.1 NC代码优化补偿技术
传统机床空间精度补偿的思路:利用初试NC代码提取各空间点坐标后代入空间精度模型中得到各空间点空间精度,但在几何误差综合影响下,各空间点会偏离至实际空间点,此时对应的空间精度为,因此将该空间精度线性逆向叠加在上后获取补偿坐标,最终以坐标进给后实现空间精度补偿,如图5(a)所示。优化补偿如图5(b)所示。

图5 优化补偿示意
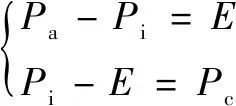
(9)
其中:为理想指令位置;为实际位置;为补偿指令位置;为补偿后的位置。
然而传统补偿结果因残差而存在局限性,由于空间精度是空间点位置的函数,传统补偿结果会导致补偿后的坐标偏离至处,并不会落在理想坐标处。因此,为规避该补偿局限性的存在,提出一种NC代码补偿技术,将传统补偿残差问题转化为NC代码最优化问题,并借助遗传算法求解实际补偿NC代码坐标,使得机床根据此优化NC代码进给后到达理想位置,即:
+=
(10)
基于式(10)搭建优化目标函数模型:

(11)
式中:=1,2,3,分别代表、、轴;n、n、i分别为实际位置、补偿量、理论位置。
该优化补偿的思想为保证优化补偿后的空间坐标与理想坐标偏差最小。
选择为优化指令坐标变量:
=(n,n,n)
(12)
根据实测实验数据可知,该空间定位精度实测数据在各轴分量均未超出0.055 mm,因此给出该优化目标函数约束条件为

(13)
根据约束条件(13),结合立式加工中心空间精度模型公式(8),利用遗传算法可求解出实际补偿NC代码坐标的目标函数。
3.2 实验验证
基于ISO230—6:2002标准,在机床工作空间内进行空间体对角线定位精度测试实验(以PPP为例),验证孔精度补偿效果。分别执行传统补偿后的NC代码和基于遗传算法求解的优化NC代码,输出机床工作空间4条体对角线传统补偿结果与优化补偿结果,如图6、表2所示。

图6 体对角线空间精度传统补偿与优化补偿

表2 体对角线空间定位精度补偿结果对比
由图6和表2可知:针对机床工作空间4条体对角线补偿,优化补偿结果均优于传统补偿结果,以PPN为例,未补偿时最差定位精度为-52.63 μm,传统补偿后定位精度得到了一定提升,此时定位精度为-18.9 μm;而通过优化补偿的定位精度为-4.77 μm,同时优化补偿率高达90.94%,消除了传统补偿后存在残差的局限性。
4 结论
面向某立式加工中心提出了一种基于遗传算法求解的优化补偿技术。基于旋量理论建立了包含21项几何误差的机床空间精度模型,并输出了该立式加工中心空间精度预测模型。对比了传统逆向叠加机床空间精度补偿技术与基于遗传算法求解的机床空间精度NC代码优化补偿技术。利用NC代码优化补偿技术对机床工作空间4条体对角线进行了补偿,且优化补偿技术相较传统补偿技术效果更加显著,该优化补偿技术消除了传统补偿后存在残差的局限性,能够更加有效地进行机床空间误差补偿。
