基于三维点云地图和ESKF的无人车融合定位方法
2022-10-12崔文薛棋文李庆玲王凤栋郝雪儿
崔文,薛棋文,李庆玲,王凤栋,郝雪儿
(1. 国能准能集团有限责任公司 机电管理部,内蒙古 鄂尔多斯 010300;2. 中国矿业大学(北京) 机电与信息工程学院,北京 100083)
0 引言
稳定、精确、实时的定位能够保证无人车行驶安全。目前无人车定位方法主要分为相对定位和绝对定位。相对定位主要采用航迹推算方法[1]和实时定位与地图构建(Simultaneous Localization and Mapping,SLAM)方法。航迹推算方法主要采用车轮里程计或惯性测量单元(Inertial Measurement Unit,IMU)[2]得到车辆位姿,但车轮里程计在车轮打滑或侧滑时会出现较大误差,IMU则在长时间使用后产生较大的累计误差,出现位置漂移。SLAM方法使用外界环境的特征来计算相对运动,对外界环境要求较高,并且每2帧数据的相对运动计算都会产生一定程度的误差,且误差随车辆行驶距离的增加而增大。绝对定位指的是在已知全局参考信息的基础上,通过传感器获得的信息计算车辆位姿的方法,不存在累计误差[3]。绝对定位包括全球卫星导航系统(Global Navigation Satellite System,GNSS)和地图匹配[4]等定位方式。无人车采用GNSS定位对卫星信号质量要求较高,对于特定场景如煤矿井下、地下隧道则无法实现定位[5]。地图匹配定位方法精度取决于已创建地图的精度,受外界的影响较小,更适用于复杂场景下的无人车定位。
先验地图构建是无人车实现地图匹配定位的重要环节。常用的地图包括二维栅格地图和三维点云地图。通过二维栅格地图可直接获取无人车的可行驶区域,但该地图对周围环境特征信息的描述较少,导致匹配定位精度低,且容易失效[6]。三维点云地图的采集范围更广,环境特征信息丰富,不仅可用于环境感知、路径规划,还可用于高精度的无人车定位。相较于相机,三维激光雷达通过主动发射激光束来直接获得与周围环境特征之间的距离信息,数据更加准确,且激光雷达几乎不受光照变化的影响。这些优良特性使得激光雷达常被用于制作精度较高的三维点云地图。基于高精度三维点云地图的无人车定位系统可以摆脱对卫星信号的依赖,不受外界环境因素的干扰。
基于激光雷达的地图匹配定位方法已成为学者研究的 重 点。M. Hentschel等[7]将OpenStreetMap数据集中的建筑物标签数据集成到机器人的定位任务中,通过激光雷达扫描得到的二维建筑物轮廓与地图进行匹配定位。F. Moosmann等[8]提出了基于迭代最近点(Iterative Closest Point,ICP)的三维激光雷达点云匹配算法,采用基于匀速运动模型的点云扭曲补偿方法进行地图构建和定位。Yang Jiaolong等[9]为了扩大ICP算法的收敛范围,结合分支定界法提出了一种全局最优解迭代最近点(Globally Optimal Algorithm Iterative Closest Point,Go-ICP)算法,通过该算法对点云进行配准。D. Droeschel等[10]提出了一种基于点云表面元模型的概率配准算法,并采用分层优化的后端图优化策略对连续轨迹和地图进行优化。然而,上述研究中所用的激光雷达点云匹配算法是以单一的特征为核心进行匹配,对于大规模点云匹配准确率较低,当2帧数据之间变化剧烈时,点云匹配算法容易发生失效问题[11]。同时,进行地图匹配定位时没有充分利用三维环境信息。因此,仅依靠基于激光雷达的地图匹配定位方法不能实现稳定、可靠的定位效果。
本文提出了一种基于三维点云地图和误差状态卡尔曼滤波(Error State Kalman Filter,ESKF)的无人车融合定位方法。采用正态分布变换(Normal Distribution Transform,NDT)算法进行点云匹配,提升大规模点云匹配准确率,并通过图优化算法解决匹配过程中误差不断累计的问题,提高三维点云地图构建精度;采用ESKF融合定位方法,实现无人车位姿信息持续稳定输出,提高无人车定位精度。
1 三维点云地图构建
1.1 激光点云匹配算法
在激光点云匹配中使用前后帧点云数据来计算车辆的相对位姿变换。激光点云匹配算法可分为3类——基于点的扫描配准、基于特征的扫描配准和基于数学特性的扫描配准。当前主要采用的是基于点的扫描配准算法——ICP类算法[12]和基于数学特性的扫描配准算法——NDT类算法[13]。ICP算法迭代计算过程比较复杂,且对初值要求较高,在大规模、高密度的点云场景下进行点云匹配时,查找对应点速度较慢,配准效率较低。NDT点云匹配的核心思想是将三维网格中的点云数据转换为连续可微的概率分布函数,即将采样得到的参考点云数据和待匹配的点云数据转换为网格中三维空间点位置的概率分布,并用正态分布表示,之后使用Hessian矩阵优化2个点云集合之间变换参数的正态分布概率,最终得到NDT点云配准结果。
利用NDT算法进行三维点云匹配的一般过程简述如下。
(1) 将扫描得到的点云集合进行网格化划分,即将三维空间中的点云划分为一个个边长相等的立方体,划分的立方体边长则为NDT算法的分辨率(分辨率大小应根据点云集合的实际情况而定)。通过每一个划分的立方体网格中的点,计算每一个网格的均值μl和协方差El:

(2) 将点云集合之间的变换参数用k表示,通过里程计数据给k赋初值或将k初始化为单位矩阵。将待配准点云集合中所有点按变换T进行变换,并转换到参考点云的立方体网格中,从而得到新的点云根据下式计算新点云落在参考点云中的概率(即待配准点云经过变换后与参考点云的重合程度):

将所有立方体网格计算出来的概率相加,得到NDT配准得分[14]:
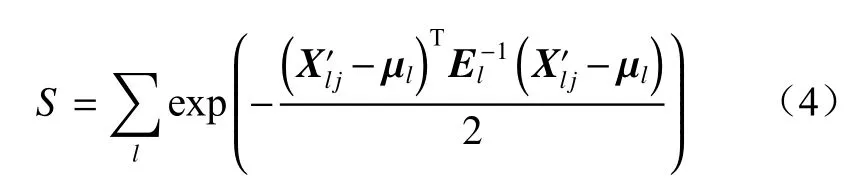
(3) 采用牛顿优化算法对NDT配准得分进行优化,得到最佳的变换参数k,使得配准得分最大。
根据上述NDT配准过程,正态分布计算是在扫描参考点时一次性完成的,相较于ICP算法,耗时稳定且计算速度较快。另外,NDT算法的计算精度与初值相关性较小,适合处理大规模点云数据,因此本文通过NDT算法进行帧间点云匹配,提高点云配准效率。
1.2 图优化算法
将激光雷达采样得到的环境点云信息和NDT点云匹配得到的无人车位姿进行关联来构建三维点云地图,在短时间内得到的是清晰度和精度较高的局部点云地图。随着无人车行驶距离增加,点云地图的构建范围逐渐扩大,扫描配准的位移误差和旋转误差也在不断累计,最终将导致不可避免的累计误差。对于构建大范围场景的点云地图而言,累计误差将导致地图局部偏移及闭环处无法闭合的现象,使得整个点云地图的精度较低。
针对地图局部偏移及地图精度低等问题,本文采用图优化算法来提高建图效果。图优化算法中的位姿图由顶点和边构成:顶点表示需要优化的参数,在建图过程中则表示无人车位姿,不包括一般SLAM问题中的路标点位姿;边表示各种约束,例如无人车不同位姿之间的相对转换关系。为减少位姿的累计漂移,提高三维点云地图构建精度,在由激光里程计获得的地图数据构建的位姿图基础上,添加闭环检测,得到闭环约束,然后通过图优化算法计算出最优位姿。闭环检测又称为回环检测,即检测无人车是否回到之前的位置,通过闭环检测可将当前关键帧与存在闭环的历史关键帧进行配准,以得到闭环位姿。将闭环位姿构成的闭环约束作为约束边添加到位姿图中。添加闭环约束的图优化原理如图1所示。
(52)合叶裂齿苔Odontoschisma denudatum(Dumort.)Dumort. 李粉霞等(2011)
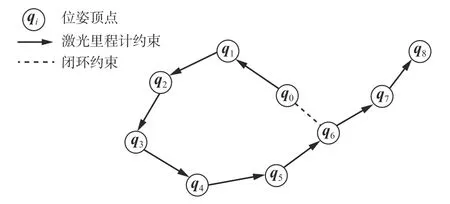
图1 图优化原理Fig. 1 Graph optimization principle
位姿图中的位姿顶点和观测约束边共同构成一个图优化问题,该问题本质上就是一个最小二乘问题。令qi(i=0,1,…,N,N为位姿顶点序号)为无人车的位姿顶点,zi和Hi分别为位姿顶点qi的观测值及观测值对应的信息矩阵。无人车位姿顶点qi和观测值zi之间的误差函数ei(qi,zi)即位姿图中的约束边。则优化问题的总体目标函数为
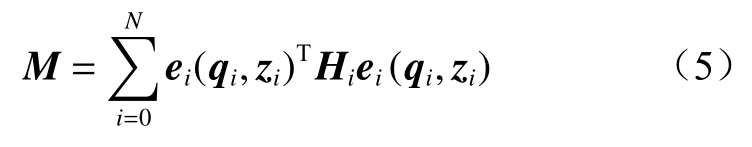
当前针对最小二乘问题的求解,主要采用高斯牛顿(Gauss-Newton,GN)算法或列文伯格-马夸尔特(Levenberg-Marquardt,LM)算法。GN算法针对非线性目标函数采用二阶泰勒展开方法,泰勒展开通常只在展开点的近似效果较好。LM算法通过添加信任区域对GN算法进行改进,使得目标函数在信任区域内的近似都有效。LM算法比GN算法鲁棒性更好,得到的结果更加准确,因此本文使用LM算法来求解整个优化问题。基于图优化的三维点云地图构建算法减少了地图的局部偏移,提高了建图精度,将为ESKF融合定位部分提供准确的三维点云地图。
2 ESKF融合定位
通过惯性导航解算(即对IMU输出角速度、加速度信息进行解算),得到当前时刻无人车的先验位姿信息(即无人车的位置、姿态和速度)。本文中,设定世界坐标系为w系,载体坐标系为b系,根据三维运动的微分性质[15]有
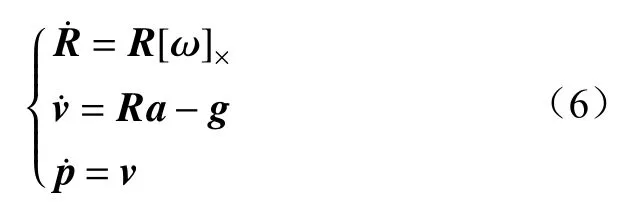
式中:R为b系到w系的旋转矩阵,即无人车的姿态;[·]×为向量的反对称矩阵;ω,a分别为IMU测量的角速度和加速度;v,p分别为无人车的速度和位置;g为重力加速度。
通过惯性导航解算可得到无人车的先验位姿信息,但解算过程中误差会随着时间不断累计。为得到更加准确的无人车姿态、速度和位置信息,采用ESKF融合定位对得到的IMU先验位姿的状态变量进行修正,需要预先建立惯性导航误差方程(式(7))。该方程由三维运动微分方程推导得到。

式中:Δθ,Δv,Δp分别为无人车的姿态、速度和位置误差;bω,Δbω,nω分别为陀螺仪的零偏、零偏误差和白噪声;ba,Δba,na分别为加速度计的零偏、零偏误差和白噪声。
使用预先构建的惯性导航误差方程对无人车的状态变量误差进行时间更新,设状态变量x=[p v R babω]T,状态变量误差Δx=[ΔpΔvΔθΔbaΔbω]T,系统高斯噪声w=[nanωnbanbω]T, 其中nba为加速度计的零偏不稳定噪声,nbω为陀螺仪的零偏不稳定噪声。由惯性导航误差方程和IMU模型,构建滤波器误差方程:

式中:F为状态变量误差转移矩阵;B为系统噪声雅可比矩阵。
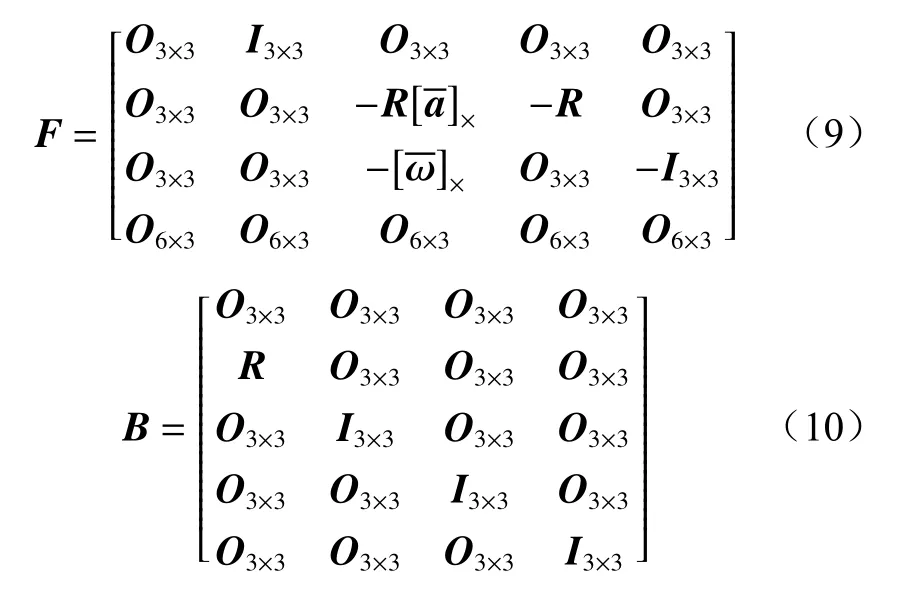
式 中:O6×3,O3×3为零矩阵;I3×3为单位矩阵;=a-ba;=ω-bω。
对状态变量误差进行时间更新后,再对其进行观测更新,即对基于地图的扫描配准数据与观测方程得到的观测值进行卡尔曼滤波。观测方程为

式中:y为状态变量误差的观测值;G为观测矩阵;C为观测噪声转移矩阵;n为观测噪声。

通过状态变量误差Δx对 状态变量x进行修正,获得无人车后验位姿,实现对传感器参数误差的补偿。
3 实验分析
3.1 实验环境和硬件平台
为全面客观地评估本文提出的三维点云地图构建和ESKF融合定位方法的性能,针对2组不同数据展开实验分析。采用由德国卡尔斯鲁厄理工学院和丰田美国技术研究院联合创办的KITTI数据集对建图及融合定位效果进行分析;在校园内开展无人车的三维点云地图构建和融合定位实验,数据采集环境如图2所示,通过定位轨迹评估融合定位效果。数据采集工作由自行搭建的数据采集平台(图3)完成,该平台搭载了Xsens MTi-300 IMU和Velodyne VLP-16激光雷达,采用软同步方式进行时间对齐。校园实测数据采集时间约为1 000 s,平台运行速度约为2 m/s,总距离约为2 km。激光雷达和IMU的外参数(即相对位姿)是数据融合的前提条件,外参标定在设置了特殊靶标的结构化环境中预先进行,因此在数据处理中将外参数作为已知量。

图2 数据采集环境Fig. 2 Data collection environment

图3 数据采集平台Fig. 3 Data collection platform
3.2 三维点云地图构建实验
为验证本文三维点云地图构建算法的有效性,与以单一特征进行匹配的建图算法(以下简称单一特征建图算法)进行对比实验。
不同算法基于KITTI数据集构建的三维点云地图如图4所示。可看出与单一特征建图算法相比,采用本文算法得到的点云地图的重影部分明显减少且轮廓清晰,其中矩形标记部分对比最为明显。KITTI数据集的实验结果表明,采用本文算法可有效提高大规模点云匹配准确率,降低累计误差和局部地图的偏移,对地图一致性的提升具有重要作用。

图4 基于 KITTI 数据集的三维点云地图Fig. 4 3D point cloud map based on KITTI dataset
不同算法基于校园实测数据构建的三维点云地图如图5、图6所示(矩形框处为无人车沿道路行驶轨迹的闭环位置)。

图5 单一特征建图算法构建的三维点云地图Fig. 5 3D point cloud map constructed by single characteristic mapping algorithm

图6 本文算法构建的三维点云地图Fig. 6 3D point cloud map constructed by the proposed algorithm
对比图5(a)与图6(a)发现,单一特征建图算法未经图优化闭环约束得到的三维点云地图在矩形框处重力方向上出现明显偏差;图5(b)可发现道路的点云沿重力方向的反方向出现明显偏移,而图6(b)中道路的点云则在同一水平面上;通过图5(c)与图6(c)的对比则更加直观地观测到单一特征建图算法未经图优化闭环约束得到的三维点云地图沿重力方向的反方向向上偏移。校园实测数据的实验结果表明,本文算法在激光里程计得到的数据基础上经图优化添加闭环约束后,能够有效处理室外大场景闭环造成的累计误差,提升三维点云地图质量。
3.3 ESKF融合定位实验
基于KITTI数据集的融合定位轨迹如图7所示。使用KITTI数据集中的GNSS数据作为定位结果的真值,选取行驶距离约为1 300 m时,基于地图匹配的定位方法和ESKF融合定位方法得到的定位数据(每隔100 m选取1个定位数据)分别与真值进行对比,得到的相对位姿误差如图8所示(横坐标为按顺序选取定位数据的序号),具体统计结果见表1。从图8和表1可看出,与基于地图匹配的定位方法相比,ESKF融合定位轨迹相对位姿误差最大值减小了0.176 9 m,平均误差减小了0.027 1 m,表明定位精度有所提升,且均方根误差减小了0.059 4 m,表明误差波动范围较小。
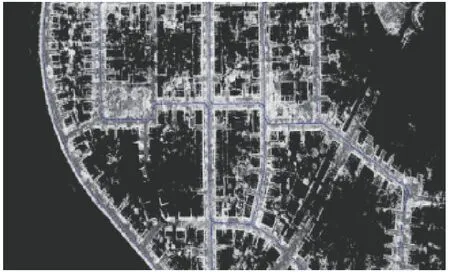
图7 基于 KITTI 数据集的融合定位轨迹Fig. 7 Fusion positioning trajectory based on KITTI dataset

图8 不同定位方法的相对位姿误差对比Fig. 8 Comparison of relative pose error of different positioning methods
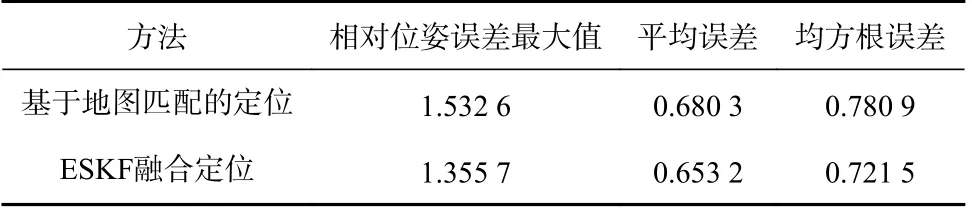
表1 定位轨迹误差统计结果Table 1 Positioning trajectory error statistics m
基于校园实测数据的融合定位轨迹如图9所示。基于地图匹配的定位方法和ESKF融合定位方法得到的定位轨迹对比如图10所示。数据采集平台实际工作时,沿图10矩形框标记路段的同一路线行驶2次,而图10(a)中矩形框标记的同一行驶路线的2条定位轨迹并没有完全重合,图10(b)中同一行驶路线的2条定位轨迹则完全重合。经对比发现,基于地图匹配的定位方法在无人车旋转时出现了配准偏差,造成2条定位轨迹不重合,而ESKF融合定位方法的定位精度及稳定性更优。

图9 基于校园实测数据的融合定位轨迹Fig. 9 Fusion positioning trajectory based on campus measured data
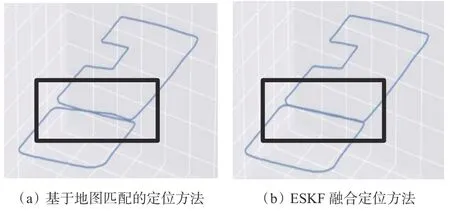
图10 不同定位方法的定位轨迹对比Fig. 10 Comparison of positioning trajectories of different positioning methods
4 结论
(1) 针对三维点云地图构建过程中累计误差较大的问题,通过激光里程计得到的数据来构建位姿图中的基本顶点和约束边,并添加闭环约束来优化位姿图。通过优化后的位姿图构建三维点云地图,地图重影部分明显减少。
(2) 针对基于地图匹配的无人车定位方法精度差且在无人车旋转时配准偏差较大的问题,采用ESKF融合定位方法,通过融合IMU数据和三维点云地图数据,实现对无人车先验位姿的修正并输出后验位姿。
(3) 实验结果表明,基于三维点云地图和ESKF的无人车融合定位方法能够有效降低相对位姿误差,在定位方面具有更稳定可靠的表现。下一步将在ESKF融合定位的基础上融合更多观测信息,如编码器测量数据,进一步提升无人车定位精度。
