基于MTF和DenseNet的滚动轴承故障诊断方法
2022-10-12姜家国郭曼利
姜家国,郭曼利
(1. 滁州职业技术学院 电气工程学院,安徽 滁州 239000;2. 国网安徽省电力有限公司 蚌埠供电公司,安徽 蚌埠 233000)
0 引言
在提升机、采煤机和通风机等常用煤矿机械设备中,滚动轴承作为基本且重要的机械元件得到广泛应用[1]。由于煤矿机械设备工作环境恶劣,容易造成滚动轴承故障[2],不仅影响煤矿机械设备的稳定运行,甚至造成严重的经济损失和人身安全事故。因此,对煤矿机械设备滚动轴承进行故障诊断十分必要。
传统的故障诊断方法有基于模型的方法和基于信号处理与分析的方法[3]。基于模型的方法需要通过对设备的机理结构进行分析,建立设备的数学模型。然而,实际中设备结构往往比较复杂,同时存在非线性和强耦合的特点,建立精确的数学模型比较困难,难以达到满意的故障诊断结果。基于信号处理与分析的方法通过分析信号中包含故障信息的特征进行故障诊断,主要分为时域法、频域法和时频域法等[4],但需要有信号处理与分析相关经验和知识的人来提取故障特征,同时由于滚动轴承振动信号成分复杂,具有非平稳和耦合等特性,故障特征提取往往较困难。
近年来,随着人工智能的发展,人工神经网络、支持向量机和聚类分析等机器学习方法开始应用于故障诊断[5],这些方法一定程度上提高了故障诊断准确率,但浅层的模型结构对复杂数据的特征学习能力有限。深度学习模型通过构建深层次网络结构,形成强大的特征学习能力,实现数据深层次特征提取和优化,从而克服了浅层机器学习方法的不足[6]。卷积神经网络作为一种深度学习算法,具有特征提取能力强的特点,被引入滚动轴承故障诊断中。张伟[7]利用数据增强技术对滚动轴承数据进行重叠采样得到数据样本,使用卷积神经网络对轴承进行故障诊断。陈晓雷等[8]使用卷积神经网络对滚动轴承原始振动数据进行特征提取,并结合双向长短期记忆和注意力机制,实现滚动轴承故障诊断。赵小强等[9]对卷积神经网络进行改进,设计了多尺度特征提取模块,实现变工况和噪声环境下的滚动轴承故障诊断。宫文峰等[10]将传统卷积神经网络的全连接部分用全局池化代替,解决了传统卷积神经网络参数多的问题,并且结合了数据增强和Dropout等技术实现滚动轴承故障诊断。
常规的卷积神经网络可通过增加网络深度来提高模型学习能力,但随着网络深度加深,会出现梯度弥散或消失,导致模型难以训练[11]。密集连接卷积网 络(Densely Connected Convolutional Networks,DenseNet)通过密集连接机制,使网络中层与层之间建立联系,加强了特征信息的传递,确保特征信息得到充分利用,从而可有效缓解梯度消失问题[12]。然而,直接将滚动轴承振动信号转换成一维或二维图像作为DenseNet的输入,往往不能保留信号间的时间相关性,导致信号信息丢失[13]。鉴于此,本文将马尔 可 夫 变 迁 场(Markov Transition Field,MTF)和DenseNet相结合进行滚动轴承故障诊断。通过MTF对滚动轴承振动数据进行编码,将一维时间序列信号转换为二维图像,使特征信息得到充分保留;将二维图像作为DenseNet的输入进行特征提取,可增强特征信息传播,使特征信息得到充分利用,从而实现滚动轴承故障精确诊断。
1 MTF
假 设 时 间 序 列X={x1,x2,···,xn},xi为 第i(i=1,2,…,n,n为采样点数)个采样信号。首先,根据时间序列取值定义Q个区域qj(j=1,2,…,Q),使每个xi都能映射到一个qj。 然后,计算各qj之间的转移概率,得到一个维度为Q×Q的马尔可夫转移矩阵[14]:
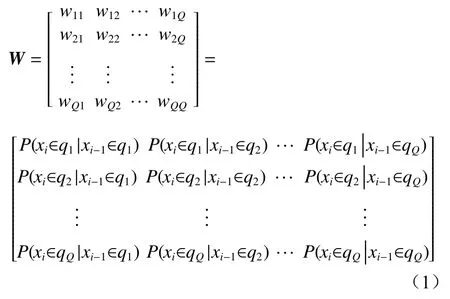
式中:wjk(k=1,2,…,Q)为区域qk中的一个采样信号后面跟随区域qj中 的一个采样信号的概率,wjk=P(xi∈qj|xi-1∈qk)。
最后,通过将每个概率按时间顺序排列来扩展马尔可夫转移矩阵,从而生成n×n的MTF矩阵M。
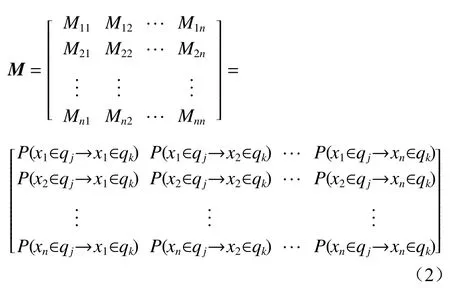
式中:Mhm(h,m=1,2,…,n)为从xh映 射的区域qj到xm映射的区域qk的 转移概率,Mhm=P(xh∈qj→xm∈qk)。
MTF矩阵M中元素取值范围为[0,1],通过下式可将矩阵中每个元素的值缩放到0~255,使其与图像中像素值对应,从而得到二维图像。
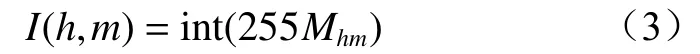
式中:I(h,m)为图像第h行、第m列的像素值;int(·)为取整函数。
2 DenseNet
DenseNet主要由密集连接块和过渡层组成[15],如图1所示。在密集连接块中任意2个密集连接层之间建立连接,实现特征信息复用,且参数少、计算高效[16]。
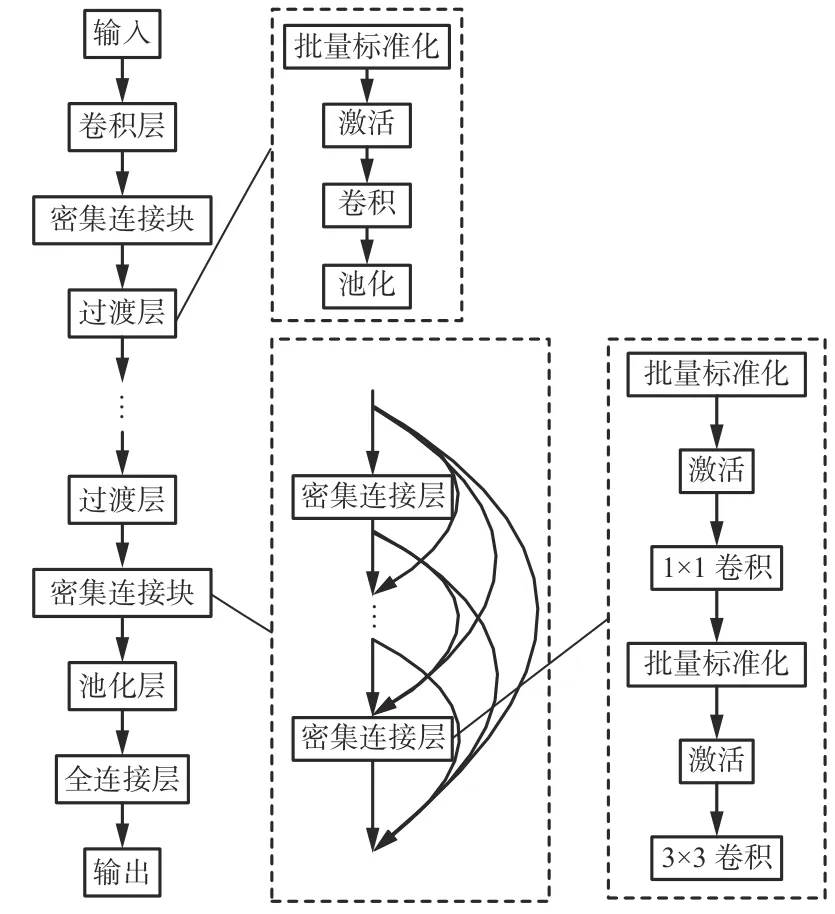
图1 DenseNet结构Fig. 1 Structure of densely connected convolutional networks
(1) 密集连接块。在密集连接块中,每一层都会接收该层前面所有层的输出作为输入。假设密集连接块有L层,则包含L(L+1)/2个 连接,第l(l=1,2,···,L)层输出为
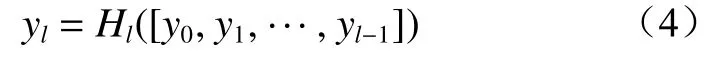
式中:Hl(·)为非线性转换函数,通常包含批量标准化、激活及卷积等运算;[y0,y1,···,yl-1]为将l层前所有层的输出进行拼接。
(2) 过渡层。过渡层是连接2个密集连接块之间的层,通过对前一个密集连接块输出的特征图进行批量标准化、激活、卷积及池化等操作,使下一个密集连接块输入的特征图数量与尺寸减小。
3 滚动轴承故障诊断模型
基于MTF和DenseNet的滚动轴承故障诊断模型结构如图2所示。
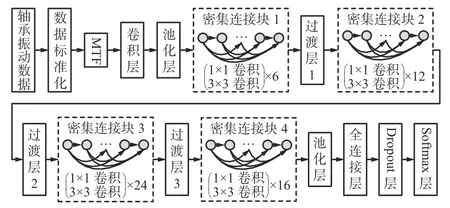
图2 基于MTF和DenseNet的滚动轴承故障诊断模型结构Fig. 2 Rolling bearing fault diagnosis model based on Markov transition field and densely connected convolutional networks
滚动轴承振动信号经过反正切函数处理,实现数据标准化:
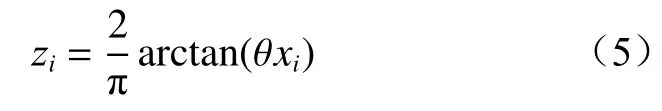
式中:zi为 标准化的数据;θ为调节参数。
标准化的数据经过MTF编码后生成192×192的二维矩阵,进而得到二维图像。将二维图像输入DenseNet网络,先经过7×7卷积层和3×3最大池化层,再经过4个密集连接块(分别为6层、12层、24层和16层)和3个过渡层(包括批量标准化、激活、1×1卷积和2×2池化),实现对二维图像特征信息的提取。最后一个密集连接块输出的特征图再分别经过池化层和全连接层,使维度降到一维。为避免模型出现过拟合现象,通过Dropout层使模型在训练过程中以某种概率忽略某些神经元,本文模型中Dropout层的舍弃概率设置为0.5。最终一维特征图通过Softmax层进行分类,实现滚动轴承故障诊断。
4 故障诊断试验与分析
4.1 试验数据
试验数据取自凯斯西储大学的轴承数据集,选取驱动端轴承正常和故障情况下,电动机载荷为0.746,1.491,2.237 kW,采样频率为48 kHz时驱动端加速度计采集的数据。驱动端轴承故障分为内圈、滚动体和外圈3类故障,每类故障的损伤尺寸分别为0.18,0.36,0.54 mm。因此,每种载荷条件下均包括1种正常状态和9种故障状态。针对每种状态采集连续的1 920个数据点作为1个样本,通过反正切函数对采集的数据进行标准化处理,标准化的数据再经过MTF转换成192×192的图像。每种状态对应生成500张图像,按照比例4∶1划分训练集与测试集,试验数据集见表1。
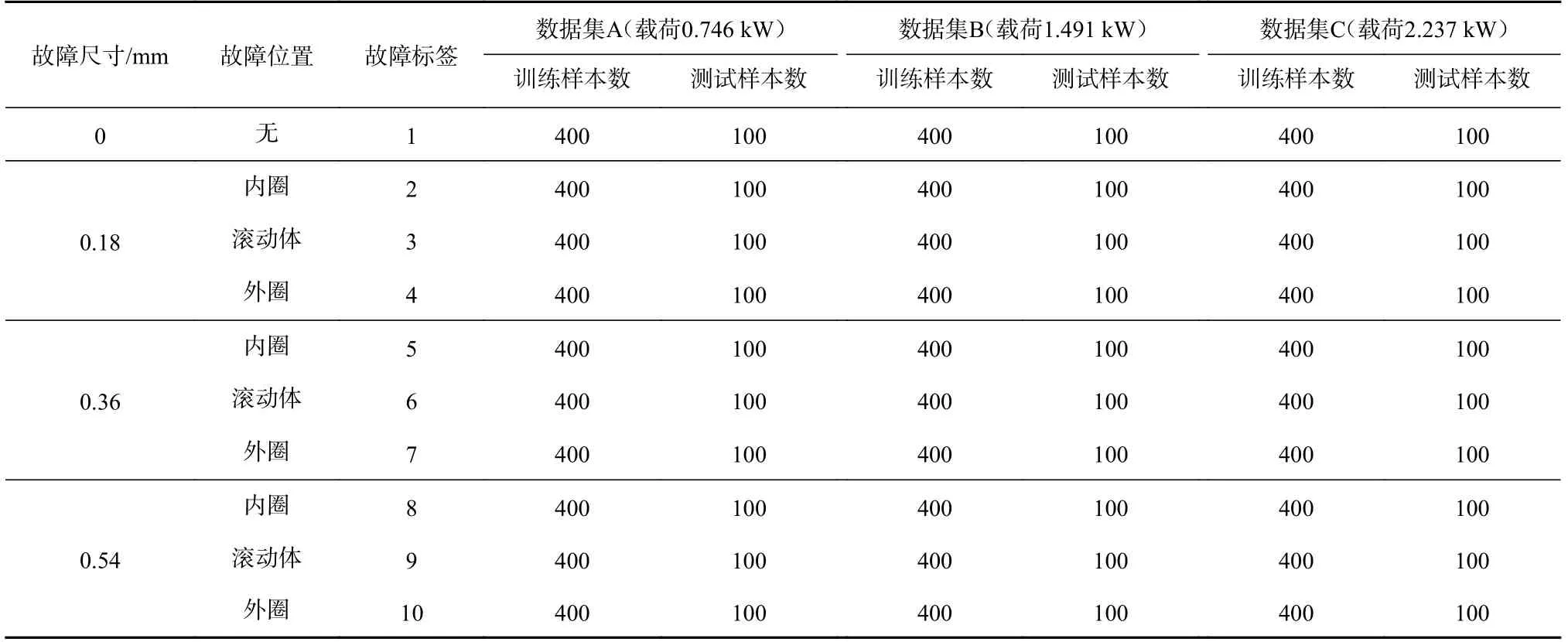
表1 试验数据集Table 1 Experimental dataset
4.2 试验结果与分析
选取电动机载荷为1.491 kW时的数据集,MTF中区域数量Q设置为16,数据标准化调节参数θ设置为2。基于MTF和DenseNet的滚动轴承故障诊断模型经过20次迭代,在训练集和测试集上的准确率如图3所示。可看出随着迭代次数增加,模型趋于收敛,准确率逐渐稳定;经过8次迭代后,在训练集上的准确率达100%;经过12次迭代后,在测试集上的准确率稳定在99.5%。
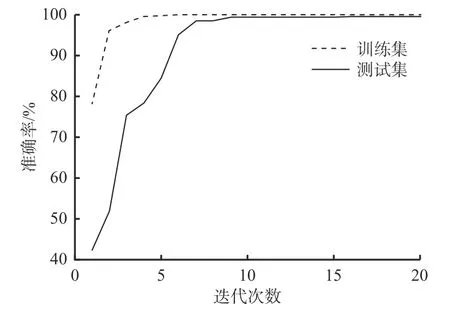
图3 故障诊断模型准确率变化曲线Fig. 3 Variation curves of accuracy of fault diagnosis model
将测试集输入训练好的模型进行滚动轴承故障分类,结果如图4所示。可看出标签为2的故障中有2个测试样本被错分为其他故障(故障标签7和故障标签8各1个),标签为7的故障中有2个测试样本被错分为故障标签2,标签为8的故障中有1个测试样本被错分为故障标签2,其他类型故障分类准确率为100%;总体来看,1 000个测试样本中有995个测试样本分类正确,准确率达99.5%。
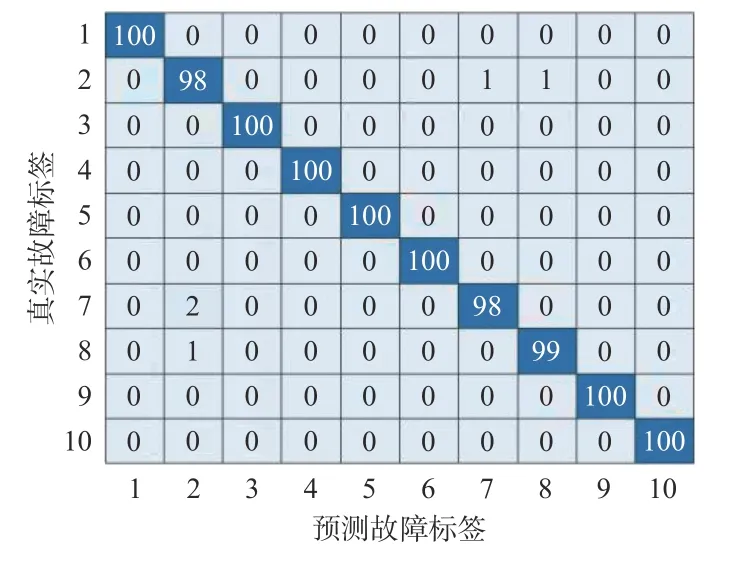
图4 滚动轴承故障分类结果Fig. 4 Classification results of rolling bearing faults
在实际中,电动机载荷往往随生产过程的变化而变化,为验证本文模型在电动机载荷发生变化情况下的滚动轴承故障诊断能力,选用电动机不同载荷下的数据作为训练集和测试集。同时为验证本文方法的优越性,选取灰度图、包络谱图、倒频谱图和MTF生成图4种网络输入图像分别与Inception和ResNet 2种网络相结合的方法进行对比。其中,灰度图按文献[17]的方法生成,包络谱图通过包络解调方法生成,倒频谱图通过倒频谱方法生成。不同方法的滚动轴承故障诊断结果见表2(A→B表示以数据集A(电动机载荷0.746 kW)的数据为训练集、数据集B(电动机载荷1.491 kW)的数据为测试集,其他情况以此类推)。可看出不同方法的故障诊断准确率在电动机载荷不变的情况下均达90%以上,其中本文方法在电动机载荷为0.746 kW和2.237 kW时准确率最高,为99.6%;不同方法的故障诊断准确率均在电动机载荷不变时高于电动机载荷变化时;本文方法在选取电动机载荷0.746 kW的数据为训练集、电动机载荷2.237 kW的数据为测试集时,准确率最低,为84.9%,但从整体来看,本文方法准确率高于其他方法,在电动机载荷发生变化的情况下仍具有较好的故障诊断能力,模型泛化性能较好。
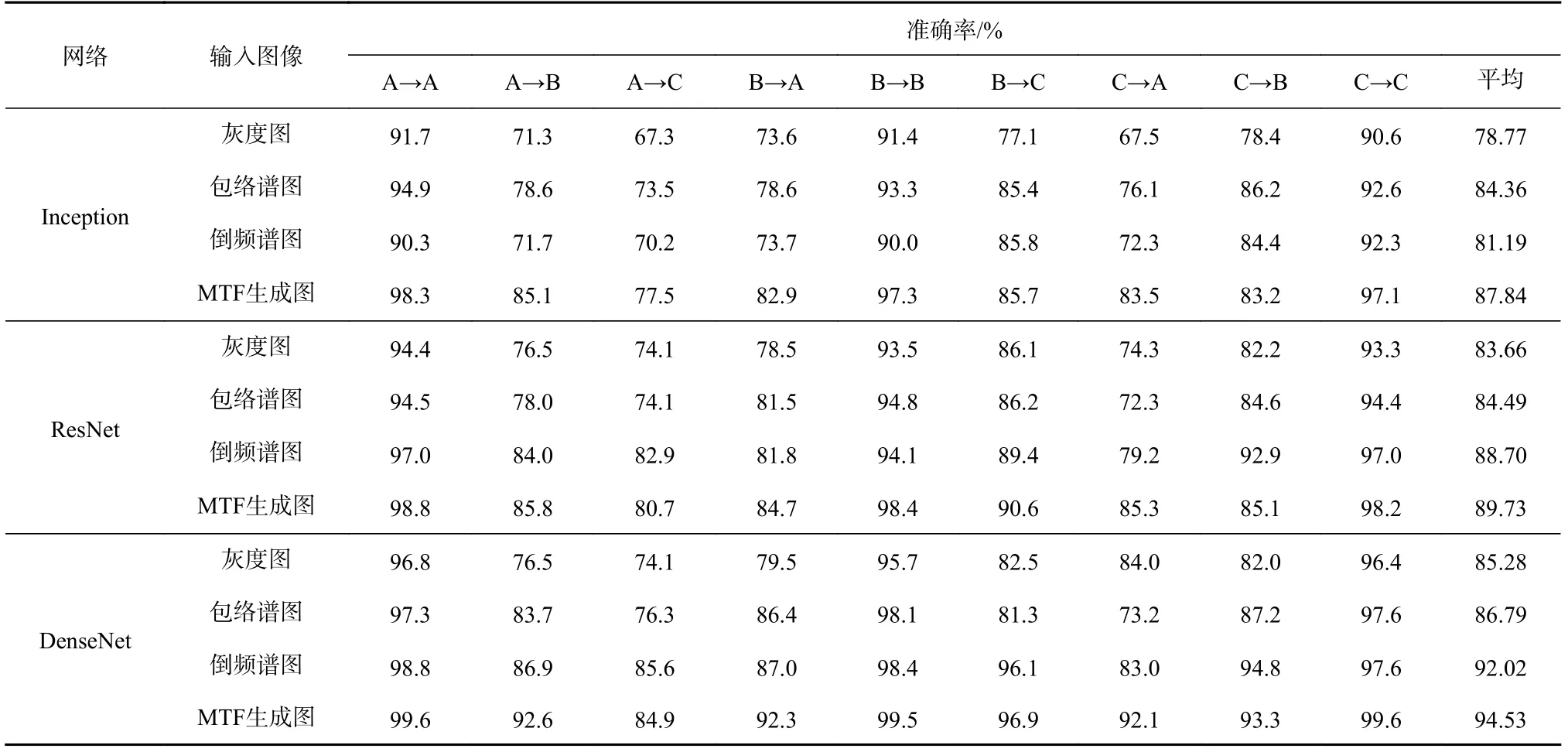
表2 不同方法故障诊断结果对比Table 2 Comparison of fault diagnosis results of different methods
5 结语
提出了一种基于MTF和DenseNet的滚动轴承故障诊断方法。采用MTF将滚动轴承一维时间序列振动信号转换成二维图像,保留了信号的时序信息和状态迁移信息;通过DenseNet对二维图像进行特征信息提取,实现故障分类识别。实验结果表明,该方法在不同电动机载荷情况下的故障诊断准确率平均值为94.53%。
