纯物质分子受到的分子间引力及其应用研究——利用平均场理论计算

＊赵仁兴

（河北科技大学 河北 050018）

分子间作用力是指两个或多个分子之间除了离子键、共价键和金属键外的其他弱相互作用力，常表现为范德华力、氢键等[1]。分子间作用力包括引力和斥力，但在绝大多数情况下，维系物质存在的是和斥力平衡后的引力。物质分子受到的引力大小决定了物质的熔点、沸点、临界温度、汽化热、熔解热、密度、表面张力、黏度、扩散系数等物理性质，同时和不同物质之间的溶解度、结晶、吸附等有关。

从1873年范德瓦尔斯建议引入引力、斥力将理想气体状态方程修正为VDW方程[2]以来，关于分子间作用力的研究一直持续不断。1912年葛生（Keeson）研究了极性分子（永久偶极矩）之间的相互作用，1921年德拜（Debye）分析了极性分子与非极性分子之间（永久偶极矩和诱导偶极矩）的相互作用，1930年伦敦（London）研究了非极性（瞬间偶极矩与诱导偶极矩）分子之间的相互作用,以后又不断推出氢键、静电作用、π-π堆积及荷电基团、疏水基团等的相互作用[1]。我国学者金松寿等[3]20世纪80年代推出了选择性分子间引力理论。

具有代表性的分子间作用力公式有两个极性分子（永久偶极矩）之间吸引的平均作用能公式[4]和分子间总的相互作用势能兰纳德—琼斯公式[5]。

上述研究极大地推进了物质物性的估算、结构的研究及新材料的制备等，但至今为止物质的吸附、色谱分离、溶解度、沸点等仍不能用分子间引力及氢键能等直接进行量化的计算，只能作些定性推断。

量子化学也将分子间力的研究作为一个重要目标。近二十年来量子化学的从头计算法有了很大发展，可用来预测分子的结构和能量，但由于分子之间作用复杂并形式多样，限制了其计算的精度[6]。

我国利用分子间引力也开展了多方面的研究，其中包括制冷剂性能、汽化热和沸点的计算、表面活性剂自组装调控、金属表面小分子吸附、共沸物的研究等[7-10]。

物质是众多分子的聚集，因此除需了解两两（例如偶极矩—偶极矩之间）分子间的作用力外，也需要得到分子在物质中受到的总引力，并且只有在了解总引力的基础上，才能更好的了解物质本身。在充分了解不同基团之间的分子间作用后就可有目标的组合不同的基团，生产更好的产品，供人类使用。

基于上述考虑，本研究采用和以前研究不同的方法计算分子间引力。物质所表现的宏观性能，应该是分子在物质内部或表面所受到的综合作用力决定的。为此该研究从分子热运动的平均场出发，利用汽液平衡时的汽化热，在不考虑不同引力种类的前提下，计算任意一个单分子在纯物质中受到其周围分子的作用力之和，本文给出了常见单质气体纯物质分子受到的引力及相应的位能，同时从引力出发给出了物质临界温度、临界压力、表面张力的计算方法，并将计算结果和实测值进行了比较，具有较高的一致性。本项目分子间引力的研究方法和传统研究有很大不同，是一种全新的分子间相互作用的研究方法。

1.研究使用的公式和推导过程

(1)静电力公式

有关研究认为分子间力为长程力[11]，作用范围为0.3～0.5nm，但和水分子偶极矩尺寸6.20×10-23nm比较，在其作用范围内仍包含有大量的其他分子。因此本研究认为纯物质中单个分子所受到的作用力，是其周围无数分子的共同作用的结果。在汽、液相变过程研究范围内，由于单个分子占据的名义体积较大，分子间的斥力对物质宏观性质尚不起决定性作用。考虑分子的热运动引起的物质同一相内分子性能的均匀性，按平均场定义纯物质中单个分子受到周围分子引力的总和为：

式中：

F—任一物质分子在纯物质中受到周围分子的引力标量之和（不考虑方向）。

f—和纯物质分子特性有关的引力系数，f也可表示为f=a1×a2，a1为某分子外其他分子对其能产生引力的综合因子；a2为某分子自身具有的能和周围其他分子产生引力的综合因子。本研究以f代替了诸如永久偶极矩、诱导偶极矩或瞬时偶极等因子，但应该是某分子原子核的正电荷或核外电子与其他分子的原子核电荷、核外电子之间的相互作用系数，同时将4πε0也纳入了f中，因此f值和以往研究的相应数值无法进行直接比较。

f′—某一对分子之间的引力系数。

n—某分子受到引力作用的分子对数。

r′—分子引力的作用半径。以往分子相互作用的研究中，一般定义r′为两个分子质心间的距离。本文定义分子引力的作用半径为某分子原子核和相邻最近分子电子云之间的距离，计算公式如下：

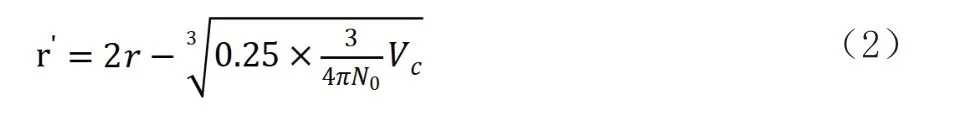
式中：Vc—临界点时的摩尔体积；

r—定义为分子的引力平衡半径。任何物质在压力、温度不变的情况下，其密度一般不会发生变化，因此可以认为在一定压力、温度下，分子所占有的名义球体体积的半径即是分子间引力平衡半径。

在单一物质均相无序状态下，分子引力平衡半径r的计算式如下：

式中：V—摩尔体积；N0—阿伏伽德罗常数。

必须说明的是r值会随物质温度、压力而发生变化。

某物质分子原子核与电子云之间的距离按该物质临界容积的0.25倍计算出的球体半径。按罗于根《元素电离能与原子的实际半径》中的计算，基态氢原子电子到核的距离为5.296×10－11m，氦原子为5.293×10－11m，两者基本一致。按氢、氦临界容积0.25倍计算出的氢分子、氦分子电子云半径分别为4.81×10-10m、4.63×10-10m，约为按电离能算出原子半径的10倍。

计算的中心分子和其外围的第二层、第三层分子等的距离可以为等表示。

本研究为简化计，不考虑周围密接分子数及不同距离的分子数，所有其他因素综合为f值。必须注意的是，因为我们采用的是汽化热计算出来的f值，因此它是周围分子对某一分子引力的综合系数，是由周围具有相同距离的分子及多个倍数距离分子共同作用的结果，这种假定的不足之处来源于：由于不同元素或化合物外层电子的多少，0.25倍Vc发生的变化；不同分子层引力的距离与单一距离的不同。

(2)汽、液相变过程中的蒸发热和单分子引力系数的计算

①汽、液相变过程中的能量

相变是物质在自然界存在的一种最重要的过程，其中包括汽—液、汽—固、液—固相之间的相变及固体结晶内部不同相的变化。

汽、液相变过程中摩尔分子吸收的热量[12]为；

②由汽化热计算单分子引力系数的公式

“汽化热包括两个组成部分，P（Vg-Vm）是液体汽化时扩大体积所需对外作的等压功，而Ug,m—UL,m是液体分子变为相同温度下的气体分子所需克服周围分子吸引力作的功”[13]。在汽液平衡时，气相和液相分子均已有相同的温度和压力，因此在分子由气相分子凝结成液相分子或由液相分子汽化为气相分子时（按分子运动论，分子的动能和压力、温度有关），不会有压力、温度的变化，分子的动能不会再发生变化，汽体、液体内分子动能是相等。因此在汽、液相变化中需要克服分子间引力的作用、需吸收外环境的热量或放出热量。

根据引力公式可得：

式中：ΔHm、ΔUm、Hgm、HLm、Ugm、ULm、Vgm、VLm—分别是汽化时摩尔焓、内能的变化及液体、气体的摩尔焓、摩尔内能、摩尔体积。P为汽化时的压力。公式（7）进行单位换算后，可用于实际计算引力系数的公式为：

式中：f—纯物质中单个分子的引力系数（kJ·m）；

M—分子量；

N0—阿伏伽德罗常数（6.023×1023）；

△HM—汽化热（kJ/kg）；

P—汽化时的压力（MPa）；

Vg—饱和气体比容（m3/kg）；

(3)单分子引力计算

根据引力系数计算公式，单个分子受到的引力计算公式如下：

式中：Vg′—饱和气体比容（m3/moL）；VL′—饱和液体比容（m3/moL）；FL、Fg—饱和液体或气体中单个分子受到的引力（N）。

(4)气相、液相摩尔分子间的引力位能计算公式

根据位能的加和性能，摩尔分子间的引力位能Eg、EL的计算公式：

式中：Eg、EL—摩尔分子引力位能（kJ/mol）；

其余符号同前。

2.常见气态元素引力系数的计算结果和讨论

(1)常见气态元素的物理性质

本文计算用的10种元素热力学数据除氯外均来源于参考文献[13-14]。

(2)常见气态元素分子间引力系数和温度之间的关系

依据式（2）定义的引力计算半径和式（8）计算出的常见气态元素单分子引力系数和温度之间的关系见图1～图5。

图1 氦3、氦4引力系数和温度关系曲线

图2 氢、仲氢、氘引力系数和温度关系

图3 惰性元素引力系数和温度关系

图4 氮、氧、氟引力系数和温度关系

图5 氯元素引力系数和温度关系

上述10种元素的偶极距均为零，说明上述元素的分子之间引力主要来源于色散力。随温度上升，不同元素的引力系数变化各有不同。第一周期氦、氢元素，无论是氦3或氦4、标准氢或仲氢、氘分子间的引力系数均随温度的上升而直线上升，说明第一周期元素色散力会随温度的上升而增加，相对偏差较大。

其他周期元素的变化相对平稳，熔点到临界点温度范围内引力系数与平均值相对偏差的平均值为0.34%～1.34%。不同元素的平均引力系数及相对偏差如下：氦3（2.23E-35，13.65%）、氦4（4.41E-35，9.14%）、仲氢（4.01E-34，7.81%）、标准氢（4.13E-34，6.92%）、氘（5.475E-34，4.70%），氖（6.33E-34，1.34%）、氟（2.66E-33，0.44%）、氮（2.52E-33，0.61%）、氩（2.71E-33，0.68%）、氧（2.97E-33，0.70%）、氪（4.01E-33，0.70%）、氙（6.07E-33，0.58%）、氯（9.66E-33，0.73%）。引力系数较大的元素，如氧、氮、氯、氪、氙等在临界点附近，引力系数有明显下降。分子引力系数越大的元素，引力系数下降越明显，可能是靠近临界点时气相中分子的聚集[15]行为所造成的。本文认为通过一个公式能将元素不同气、液相饱和温度下4种数值相差很大的数据，计算出一个表征元素分子间引力并相对一致的数值，即使计算出的引力系数不是绝对正确，但这一相对稳定的数值体现了该元素的一种本质属性，应具有较大的物理意义。

(3)不同元素引力系数的比较

不同元素引力系数变化的规律为：

①在周期表同一周期中外层电子数饱和的惰性元素引力系数最小，其他元素的引力系数相近，但随外层电子数增加依次有所增加；

②在周期表同一列中，从上到下外层电子数越多，引力系数越大，也说明了分子间引力是原子核正电荷与核外电子的相互作用所引起的。

(4)单个分子的引力、克分子引力位能的计算结果

依据公式（9～12），不同元素计算温度范围内，饱和液相、汽相单个分子受到的引力和的克分子引力位能（焦耳）如下：氦3（32-44.7，3.63-35.3）、氦4（85-103.4，11.1-61.8）、仲氢（809.9-919.4，60.8-511）、标准氢（703.62-854.52，62.8-561）、氘（1099-1232，107.3-652），氖（1241-1743.7，161-911.4）、氟（4819-7209，91-2761）、氮（3537-5792，345-2947）、氩（4223-6407.8，547-3232）、氧（547-3232，85-3575）、氪（5929-8930，743-4423）、氙（8741-12423，1046-5657）、氯（20861.7-12974，865-8774）。在气液平衡状态下不同温度时气体或液体内的单分子受到的引力是不同的，在所计算的物质中氦3分子受到的引力最小，氯分子受到的引力最大；依据临界点附近的数据外推得到临界位能和临界温度的关系是正相关，相关系数达到0.998699。由于温度是分子动能的量度，在分子的动能和位能达到某一平衡时会出现临界状态。

图6、图7给出了氧元素汽、液相中克分子引力位能及单个分子受到引力随温度的变化。随温度上升，液相中的单个分子受到的引力的下降速率大于引力位能的下降速率；汽相中单个分子受到的引力的上升速率小于引力位能的上升速率。

图6 汽液相中克分子氧的引力位能随温度变化

图7 汽液相中氧分子受到的引力随温度变化

将同一温度下汽、液两相克分子位能进行平均，其平均值和温度线性相关系数基本接近于1，说明汽、液平衡时分子动能和分子间的位能应满足一定的关系，图8给出了氦4的示例。

图8 氦4液汽相克分子位能的平均值和温度的关系

(5)和其他方法计算出的分子间力的比较

《建立分子简化模型用经典电磁理论探析分子间作用力》说明了分子间引力、斥力、分子电流安培力之间的关系[16]，同时计算了氦分子的分子间力，本计算和其计算出的引力比较见表4，差别未超过数量级，计算结果有可比性，同时说明了本文计算出的分子间引力具有一定的可靠性。

表1 氦分子间引力计算结果和其他研究结果的比较

3.利用分子间引力计算物质的临界温度和压强

(1)分子间引力和临界温度、压强关系式推导

对式（8）进行变换，增加一个不可压缩的量则可得到下式：

经推导到临界点：

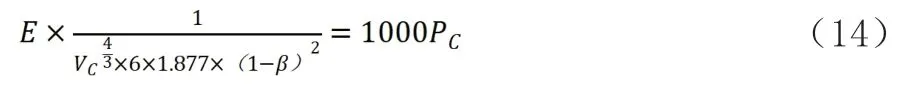
式中：E—平均公斤引力系数（kJ·m·kg-4/3），E=f/

Vc—临界容积（m3/kg）；

β—临界态修正系数，无量纲；

Pc—临界压强（MPa）。

该式说明临界点的气压和物质引力系数与（Vc）^（3/4）的倒数乘积成正比。

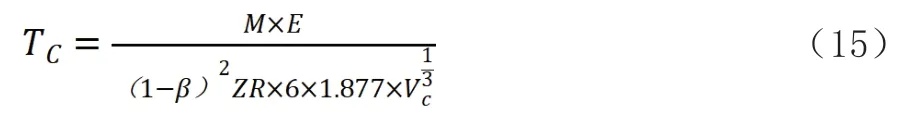
式中：R—8.3145（kJ·mol-1·K-1）；Z—压缩因子。

(2)计算结果和讨论

①相关方程计算结果

图9、图10分别给出了第一周期五种元素、同位素和其余元素分子间引力系数（沸程内的平均值）和临界体积4/3方倒数的乘积与临界压强的关系曲线，R2分别达到0.9679和0.9805，利用相关系数反算出的临界压力见表2，计算结果表明误差在可接受范围内。图11、图12、图13、图14给出了分子间引力系数（沸程内的平均值）和临界体积^（1/3）方倒数的乘积与临界温度、沸点关系，同样具有良好的正相关性。结果证实了本文提出引力关系式的推论，间接证实了利用汽化热计算分子间力的可行性，同时可以看到分子间引力系数越大，物质的临界点、沸点温度越高。

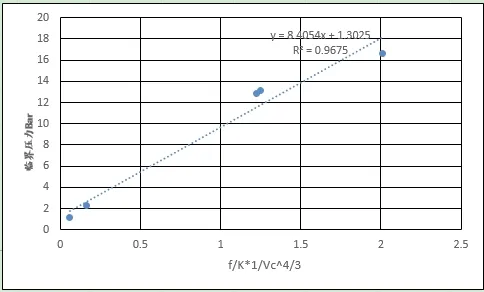
图9 第一周期元素引力系数/临界体积^（4/3）的关系

图10 其余元素引力系数/临界体积^（4/3）的关系

表2 利用回归曲线计算出的临界压力和临界温度

图11 引力系数/临界体积^（1/3）与临界温度关系

图12 引力系数/临界体积^（1/3）与沸点温度关系

(3)通过引力公式直接计算临界压力、临界温度

由公式（14）（15）可知，在由分子间力计算临界压力、临界温度时需要确定β值。在不作β修整时，采用的引力系数是元素沸程范围内的引力系数的平均值，每个元素代入压缩因子Z为实际压缩因子条件下计算出的临界温度、临界压力和实际值相差较大，不同元素临界压力相对误差绝对值为16.81%～53.78%；临界温度为8.24%～53.86%。但考虑到是由引力直接计算出来的，临界压力、温度的误差在50%以下，应当说引力的假设是基本成立的。每个元素求得的临界压力、临界温度修正值β，除氦4外，温度修正的β和压力修正的β值基本一致，氩、氪、氙、氮、氧、氟、氯为-0.1351～-0.2158。第一周期元素的β变化较大，标准氢、仲氢、氘、氦4、氦3临界压强的β值分别为0.08896、0.0791、-0.0407、0.2109、0.319，临界温度的β值分别为0.0672、0.0791、-0.0407、-0.1747、0.3193。

4.由分子间引力计算饱和液体的表面张力

(1)公式推导

至今尚未有直接利用分子间力计算表面张力方法，现拟采用计算出的引力计算不同温度下的表面张力。在液相和气相的边界层被认为是具有和气相、液相完全不同性质的第三相。由于边界层（表面相）两侧承受到的吸引力不同，表面处于张紧状态，并倾向于保持最小的表面积。表面张力一般用γ表示，定义为表面上单位长度的力，达因/厘米。纯质液体表面张力的估算公式有：Quayle的等张比容法、Sastri的对比关联式等，产生的误差一般在5%以内[17]。

汽液两相接触时，由于两相内部引力不同，液体表面自由能ΔG=γdS。在等温等压下，液体形成新表面时吉布斯函数的变化应等于除体积功外的其他功。依据前面的公式，该功应是分子间引力所作的功。根据推理，形成新的汽液表面时，分子间引力作的功为：

公式的前一部分是指的液体分子由内部进入表面时克服液体分子间引力所作的功；后一部分为气体分子和液体分子接触形成表面时，气体分子引力所作的功。

式中：f—分子间的引力系数。n—某进入液体表面的中心分子最邻近的分子数，为满足表面自由能最小的条件，每个表面分子一般只失去一个邻近分子，因此为1/n，实际引起表面张力不仅是第一层分子，也有其他层的分子，因此n一修正量，dS/π。r2—单位表面积含有的分子数。r—液体分子名义半径；积分第一项为分子引力由液体内半径为r进入表面到半径为过程中作的功；后一项为dS面积上气体相对于液体分子数的比例及气体分子由气体内进入到汽液表面气体分子内引力作的功，实际气体也有多层分子做功为此加入第二修正量m。汽液界面上气体分子和液体分子受到的引力应该相等，因此：

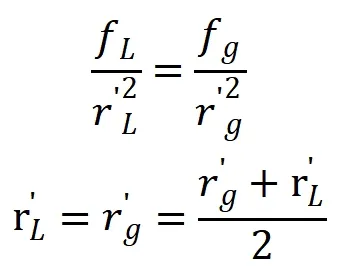
积分后公式为：

对公式进行单位换算，则得汽液相平衡时液相表面张力如下：

式中：γ—表面张力（μN/m）；VL、Vg、VC—液体、气体、临界比容（m3/kg）；M—分子量；n、m—修正系数。

(2)计算结果和讨论

由不同物质表面张力的计算结果可知，查表结果和计算结果有一定误差，但未超过数量级。

不同元素的表面张力误差的计算结果见表3。结果表明计算不同元素表面张力的误差不同，其中氖和氩元素的误差最大，其他一般在5%～15%之间。不同元素的修正值不同，但多种元素的N值4.5～5，M值在0.5～0.61。不同元素M、N值的不同或计算和查表结果不能完全符合的原因可能和表面分子之间的结构有关。

表3 其他元素表面张力计算的误差

5.结论

（1）利用汽化热计算和利用经典电磁理论计算得出的氦分子间引力基本一致，说明提出的方法适用于饱和态汽、液分子间引力的计算。（2）第一周期元素的分子间引力系数随温度上升而增加，其他周期元素的引力系数随温度上升有不同的变化但和平均值的偏差多数在1%以内，引力系数越大的元素，到临界点附近引力系数有明显下降。在同一周期中外层电子数饱和的惰性元素引力系数最小，其他元素的引力系数相近，但随外层电子数增加依次有所增加；同一列中，从上到下外层电子数越多，引力系数越大。原子核内的中子数量对引力系数有影响，电子的自旋方向对引力系数的影响较小。（3）计算元素临界点的单分子受到引力为10-13～10-11N，克分子引力位能为39～10000J；元素克分子引力位能和元素的临界温度线性相关，相关系数达到0.9987。元素临界压力与平均引力系数和临界体积4/3次方倒数的乘积正相关，元素临界温度与平均引力系数和临界体积的1/3次方倒数乘积正相关。利用推导出的公式可以计算出元素的临界压力和临界温度。（4）利用计算出的分子间力可通过推导出的公式计算出饱和液体的表面张力，部分元素的计算结果可满足工程要求，部分元素计算出的结果和查表值误差较大，原因可能在于不同元素汽、液的分子结构不同有关。（5）上文是分子间力定量化计算的一种有意义的方法，将会促进分子间引力研究的发展，为改善物质性能或生成新物质提供科学依据。