城市道路交通瓶颈识别算法研究
2022-10-12冯嘉松杨国平徐启禄
冯嘉松,杨国平,徐启禄,罗 强,帅 祥
(1.成都信息工程大学 软件工程学院, 成都 610225;2.青岛地铁集团有限公司, 山东 青岛 266100)
0 引言
随着城市化发展,城市居住人口呈现爆炸式增长,给城市交通带来了巨大压力,交通拥堵已经是所有现代化大城市难以解决的严重问题[1]。交通拥堵不仅影响人们日常出行,降低交通基础设施的工作效率,同时也对生态环境造成了一定程度的破坏,进一步导致了各种社会和经济问题[2]。
城市交通压力主要来自于交通瓶颈,分析城市道路交通瓶颈并进一步得到拥堵扩散趋势,可以为改善城市拥堵提供技术支持。通常情况下,在瓶颈处进行道路拓宽、信号灯优化、道路封禁等措施都可以缓解交通拥堵,降低城市车辆通行的压力[3-4]。
在以往的研究中,大多数学者将目光着眼于高速公路上[5],因其具有结构简单的特点,然而在实际生活中,城市道路网络中的瓶颈识别更加迫在眉睫。首先,城市道路网络错综复杂,对路段因果关系的分析更加困难。其次,城市道路网络中可能发生的意外情况更多,对模型如何去除这些“脏数据”要求更高。最后,高速公路上几乎没有信号灯,但城市道路网络中有大量的交通信号灯,对交通路网中车辆的通行能力影响很大。
现有的城市道路交通瓶颈识别技术大多关注拥堵路段本身,在考虑拥堵扩散效应上还有所空白,这样找到的瓶颈并不是缓解拥堵的最优解,很多时候对拥堵的缓解效果甚微,甚至可能是错误的瓶颈。为了正确的描述交通瓶颈,本文考虑以下2个主要特征:① 路段本身的拥堵程度;② 该路段的拥堵对周边路段造成的影响。
为了填补目前该方向研究的空白,本文从拥堵扩散的角度对交通瓶颈做了全新定义,提出了一种全新的交通瓶颈识别算法,能更有效地识别交通瓶颈。此外,本文使用SUMO仿真工具来验证所识别的交通瓶颈,并在实际场景中进行了测试。具体来说,本文贡献如下:
1)基于拥堵路段本身及其对周边路段的影响,对拥堵瓶颈做了全新的定义,可以更好地描述拥堵路段之间的因果关系,这样得到的拥堵瓶颈更为准确。
2)提出了一种全新的城市道路交通瓶颈识别算法,通过图论法模拟城市交通路网,采用时间序列分析方法计算拥堵扩散程度,最终将拥堵路段对城市交通造成的负面影响数值化,确定交通瓶颈。
3)使用SUMO仿真工具进行瓶颈验证,并与现有的方法进行横向对比分析,论证了使用本文所提出的方法可以更有效地缓解交通拥堵,并在真实路网中也进行了实证。
1 相关工作
1.1 基于路线引导的拥堵缓解方法
交通拥堵是现代社会一个长期存在且日益严重的问题。在路线引导方面,重新路由的方法被广泛用于以更有组织的方式管理交通网络,缓解道路网络的拥堵。杨留辉等[6]将重路由的方法和信号灯的控制相结合,利用交通摄像头采集的道路信息分析行人与车辆的运动状态,动态优化信号灯配时方案,从而加快行人和车辆通过路口的时间。实验证明,该方法可以有效增加人们出行的效率,降低交通拥堵发生的概率。Huo等[7]同样提出了一种基于聚类的交通拥堵避免混合重新路由系统(clustering-based hybrid re-routing system for traffic congestion avoidance,CHRT)。CHRT开发了一种多层混合架构,中央服务器访问流量的全局视图,分布式部分由分成集群的车辆组成,以减少延迟和通信开销。然后,提出了一种基于聚类的优先级机制,基于实时交通信息设置聚类优先级,避免二次拥堵。Cao等[8-9]综合考虑到达时间和总旅行时间,先后提出了一种分散的基于多主体的路线引导方法和半分散的基于多智能体的路线引导方法。
1.2 基于路段自身拥堵程度的瓶颈识别技术
路线引导方法是在交通拥堵发生后用于缓解交通压力的手段,需要在多个路口应用交通控制策略,在一定程度上可以缓解交通拥堵,但无法从源头处解决问题。因此,先确定路网中导致拥堵的关键位置,再实行交通控制策略,可以达到事半功倍的效果。 Thilakshan等[10]利用众包实时旅行时间数据识别瓶颈,这在收集和分析方面更为有效。Chen等[11]提出了一种基于梯度增强决策树(gradient boosting decision trees,GBDT)的方法来识别道路网络拥堵的根本原因,并使用不同类型的解释变量对影响因素进行排序。以苏福尔斯网络为例,利用SUMO仿真工具对不同交通流量下不同交叉口和路段车道数的信号控制策略,对GBDT模型进行训练和测试。
1.3 基于拥堵路段因果关系的瓶颈识别技术
作为分析城市交通瓶颈的新视角,路段的拥堵扩散最近受到了广泛关注。Nguyen等[12]引入了一种基于拥堵扩散因果树的算法,该算法演示了路段的拥堵扩散趋势,并基于拥堵的时间和空间信息估计了它们的扩散概率。Tao等[13]采用一种基于细胞传输模型(cell transmission model,CTM)的交通流模型进行复杂城市交通环境的模拟,建立了以链路为节点的链路状态图来分析节点之间的关系。在文献[14]中也得出了同样的结论,Yong等[14]通过网络个体之间的协调博弈和交通拥塞过程中旅行者的决策行为,描述了交通网络中拥塞的扩散过程。实验表明,当拥堵扩散影响达到某一临界阈值时,必须采取适当措施控制局部交通拥堵的扩散才不会发生大规模的交通拥堵。
基于上述研究,研究者们进一步提出了一些直接或间接考虑拥堵扩散的城市交通瓶颈识别方法。Ma等[15]提出了一种基于复杂网络理论和用户均衡模型(user equilibrium,UE)的关键瓶颈识别算法。该方法综合考虑了部分路段失效前后网络有效性和差旅成本的变化。然而,由于流量阻抗和网络有效性难以计算,该方法识别出的瓶颈还有待验证。除此之外,该方法在识别瓶颈时没有明确考虑路段之间的拥堵扩散情况。Zhao等[16]从一个新角度来解决交通瓶颈识别问题:交通流量影响(traffic flow influence,TFI)最大化。该模型基于交通拥堵扩散(traffic congestion diffusion,TCD)模型并与TFI相结合,可以解释交通状况的变化,并捕捉道路网络的动态。然后将交通瓶颈识别问题简化为TCD条件下的NP-hard影响最大化问题。Li等[17]也研究了一种考虑拥堵扩散效应的瓶颈识别方法,但是路段之间的相关性分析不够严谨,没有考虑长时间范围内的相关性,并且拥堵路段扩散成本的定义和计算尚待完善。
2 瓶颈识别技术
2.1 瓶颈识别技术工作流
城市交通瓶颈识别模型的主要步骤包括:
1) 首先获取城市交通路网以及某个长时间段里的车辆运行轨迹数据,对路网数据进行图论建模,使用仿真软件还原实际交通状况。
2) 然后分析各路段拥堵状况,进一步分析拥堵路段之间的空间位置关系、因果关系,得到拥堵扩散趋势图。
3) 最后分别计算拥堵成本和扩散成本,量化了拥堵路段对交通路网产生的影响,从而确定交通瓶颈。
本文所提出的城市交通瓶颈识别模型需要一系列相应辅助模块共同协作,其工作原理如图1所示。

图1 瓶颈识别系统框架图
2.2 拥堵路网识别
交通拥堵的性质通常情况下分为常发性和偶发性,城市道路的偶发性拥堵主要是由事故、特殊事件以及极端天气造成的,相比之下,偶发性的识别比较困难,通常被视为一种模式的识别[18-19],并使用许多分类器来确定拥堵的位置和严重程度。本文关注的重点是常发性拥堵瓶颈识别。
2.2.1道路状态识别
车辆行驶速度作为评估道路状况的重要指标,目前相关研究已经沿多个方向进行。现在关于机器学习、神经网络的技术越来越成熟,在与交通有关的预测中也使用了许多常用的神经网络,如循环神经网络(recurrent neural network,RNN)[20]和Elman神经网络[21],这些方法大多利用车辆平均行驶速度来对路段状态进行分类。在本文中,为了识别道路是否拥堵,以道路车道占用率以及停滞车辆长度作为指标。相比之下,这样比利用车辆平均行驶速度作为指标更能表述路段拥堵状态。具体来说,假设一条路段上车辆的总长度与路段总长度之比为Len%,路段上停滞车辆数与总车辆数之比为Amo%,如果Len%大于M%并且Amo%大于N%,则判定路段在该时刻为拥堵状态。其中M和N的值根据具体城市而定,通常情况下,M∈[50,80],N∈[40,70],具体判别标准如表1所示。
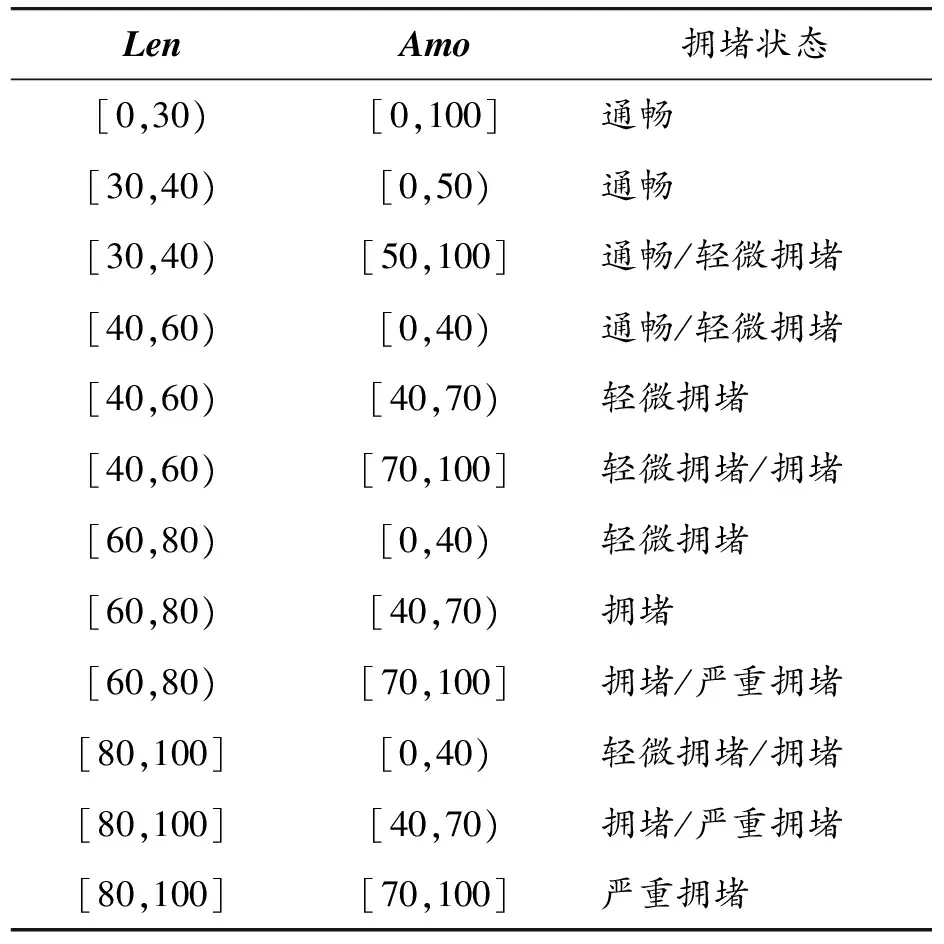
表1 拥堵状态判别标准
定义1(车辆轨迹数据):车辆轨迹数据定义为Trai={lane1,lane2,…,lanen},Trai为车辆i的轨迹,lanen为路段编号,n不超过路网中路段总数。
利用车辆轨迹数据和相应地图数据,通过仿真软件可以还原实际的交通状况,分析出路网中拥堵路段集合,进一步结合路网拓扑结构可以得到拥堵路网拓扑结构。
传统方法和对偶方法是提取复杂道路网络的2种常用方法。传统方法将交叉口视为节点,将路段视为节点之间的边,该方法可以反映城市路网的物理结构。采用对偶方法,路段由节点表示,相邻路段的连接用边表示[22]。本文重点关注的对象是路段,分析拥堵路段之间的因果关系。因此,本文采用对偶方法将城市道路网表示为一个有向图网络。具体定义如下。
定义2(路网拓扑结构):路网拓扑结构表示为一个图Map=(V,E),V是顶点集,由所有路段组成,E是边集,由路段之间车辆行驶方向组成,每一条边就是一个点对(u,w),其中u、w∈V。
2.2.2拥堵路网拓扑结构
路段之间的拥堵往往不是独立存在的,它们互相影响,相互牵制,当一条路段发生拥堵后,周围路段都会受到影响,导致其通行能力下降。为了清楚地描述拥堵路段之间的联系,需要构建拥堵路网拓扑结构,拥堵路网拓扑结构描述了拥堵路段之间可能的因果关系。
定义3(拥堵路网拓扑结构):将顶点集V表示为拥堵路段集合的路网拓扑结构称为拥堵路网拓扑结构。
以每个拥堵路段作为根节点,在路网拓扑结构中进行遍历筛选,找到符合以下条件的边〈u,w〉来构成拥堵路网拓扑结构:
1) 节点u、w均发生过拥堵,并且w先于u发生拥堵。
2) 节点u、w最短路径距离必须小于阈值。
给出一个简单示例。如图2所示的路网,包含44个路段,将路网中的路段看成一个节点,道路行驶方向看成一条边,图2所示的路网可以通过图3的拓扑结构来表示,其中红色节点表示该路段在整个时间段中发生过拥堵。进一步筛选符合拥堵路网的拓扑关系,得到拥堵路网拓扑结构,如图4所示,其中边表示拥堵路段之间可能存在的牵制关系。

图2 实际路网图

图3 路网拓扑结构图
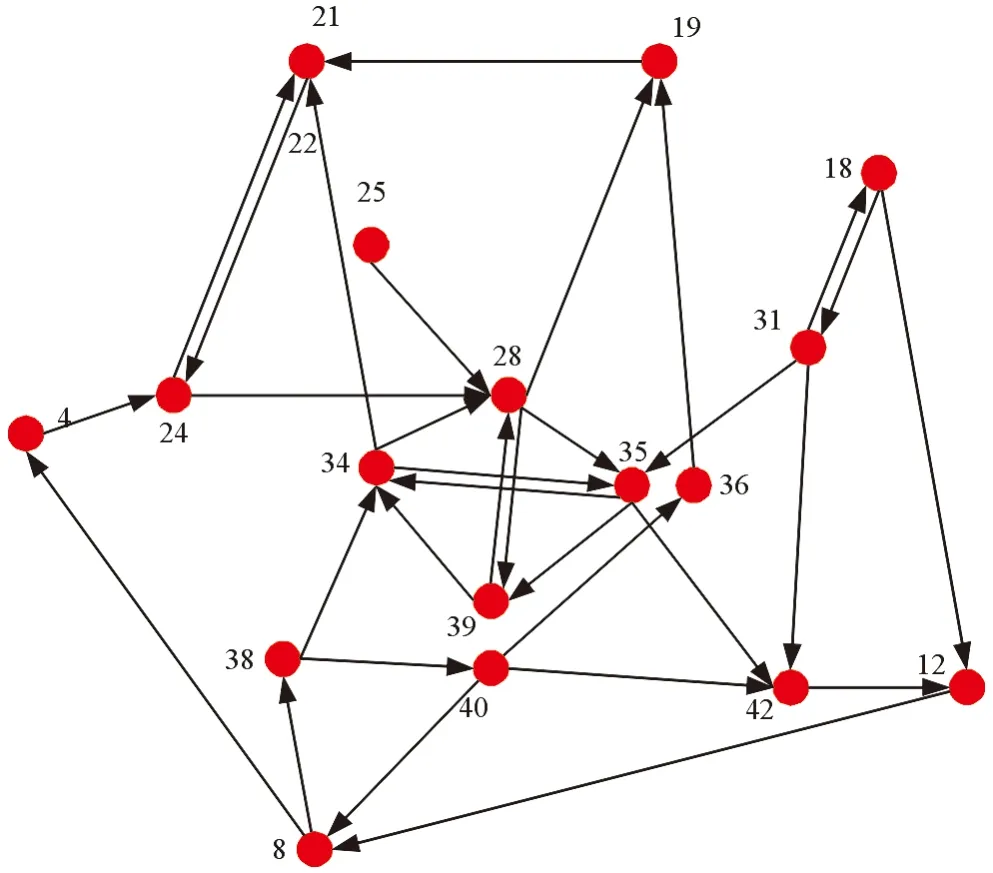
图4 拥堵路网拓扑结构图
2.3 扩散趋势识别
路段的拥堵都会向周围进行扩散,拥堵路段和被影响的路段从长时间来看必然存在一定的因果关系。本小节分析了拥堵路段的因果关系,在此基础上得到了拥堵路段的扩散趋势图。
2.3.1拥堵路段因果关系分析
本文通过拥堵状态构成的时间序列来进行因果关系判断,相关定义如下。
定义4(路段i的拥堵状态时间序列):给定一个路段lanei,则称Seqi={STi1,STi2,…,STit|STit=0,1}为路段lanei的拥堵状态时间序列,STit表示路段lanei在时刻t的拥堵状态,值取1表示路段拥堵,0表示路段通畅。
由于路段之间的拥堵存在时差,不是实时相关的,因此采用时间滞后互相关(TLCC)来确定拥堵路段之间的因果关系。
定义5(时间滞后程度):lanei的拥堵在时间k后扩散到lanej,则时间差k称为两路段的时间滞后程度。
TLCC用于计算时间滞后互相关程度,主要分为两步:① 构建时间滞后的拥堵状态时间序列;② 计算拥堵状态时间序列互相关程度。
首先需要构建每个路段不同时间滞后程度的拥堵状态时间序列。假设lanei的拥堵状态时间序列为Seqi,时间滞后程度为k,lanei的时间滞后拥堵状态时间序列NSeqi的构建过程如图5所示。
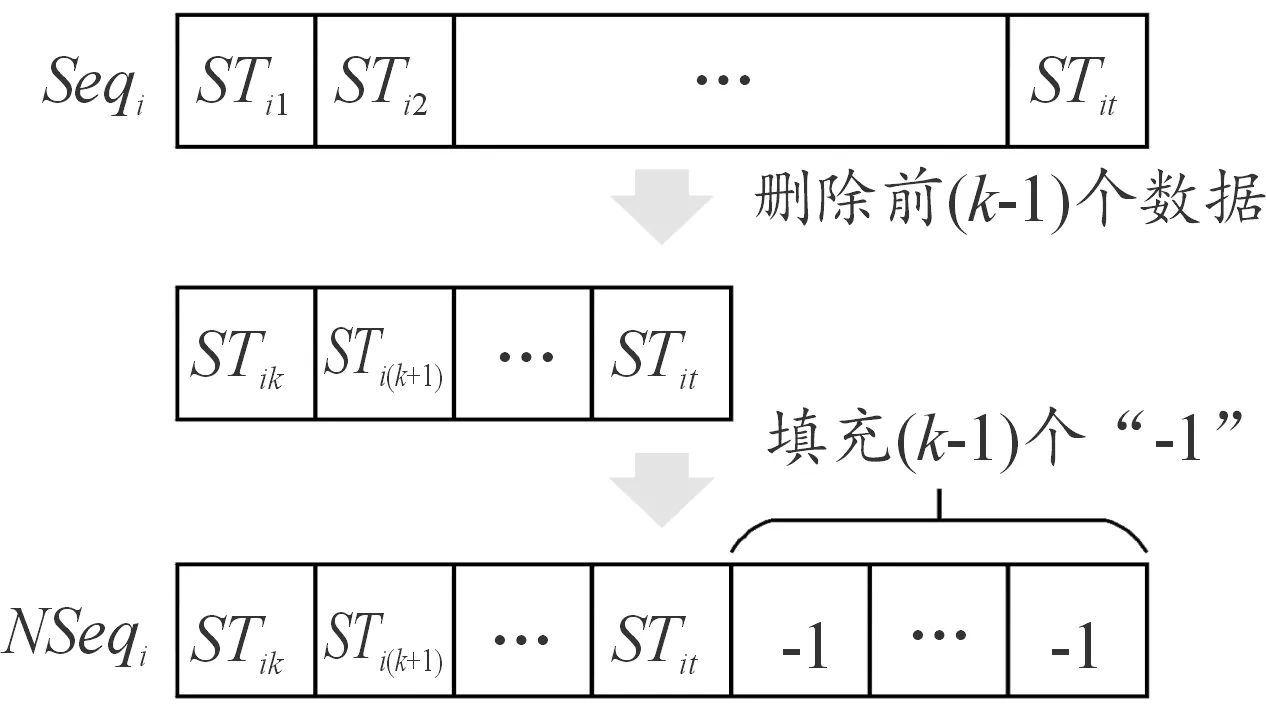
图5 时间滞后的拥堵状态时间序列
通过上述步骤可以得到每个拥堵路段的时间滞后拥堵状态时间序列,进一步可以分析2个拥堵路段之间时间滞后拥堵状态时间序列的相关联程度。
本文采用皮尔逊相关系数来计算两路段拥堵的相关程度,通过相关系数来描述拥堵的因果相关程度,皮尔逊相关性系数见式(1):
(1)
式中:cov为协方差,σ为标准差,Ε为期望,X、Y依次为拥堵路段的拥堵状态时间序列和被影响路段的时间滞后拥堵状态时间序列。可以进一步化简为式(2):
(2)
当计算出相关系数后,可以通过以下取值范围判断变量的相关强度,如表2所示。

表2 相关系数强度
定义6(拥堵路段间因果关系):给定2个拥堵路段lane1和lane2,lane1的拥堵状态时间序列为Seq1,lane2的时间滞后拥堵状态时间序列为NSeq2,如果两路段时间滞后互相关程度(TLCC(Seq1,NSeq2))超过阈值(r),则称lane1和lane2拥有因果关系。具体分析见式(3):
(3)
式中:R表示拥堵路段间因果关系,R=1代表拥有因果关系,R=0代表没有因果关系;TLCC(·)为计算两拥堵路段时间滞后互相关程度的方法;r为指定阈值。
假设lane1和lane2时间滞后互相关如图6所示,横坐标表示时间滞后的程度,纵坐标表示每个滞后时间点的互相关程度。从图中可以得到,在时间滞后程度为0时,2个路段互相关程度较小;在滞后6个时间点时,TLCC(Seq1,NSeq2)=0.689,假设滞后6个时间点符合时间滞后范围,且r取值小于0.689,则R(lane1,lane2)=1。
2.3.2扩散趋势图分析
通过对拥堵路网进行因果分析,从而得到每个拥堵路段的扩散趋势图,用于描述拥堵向周围扩散的情况。
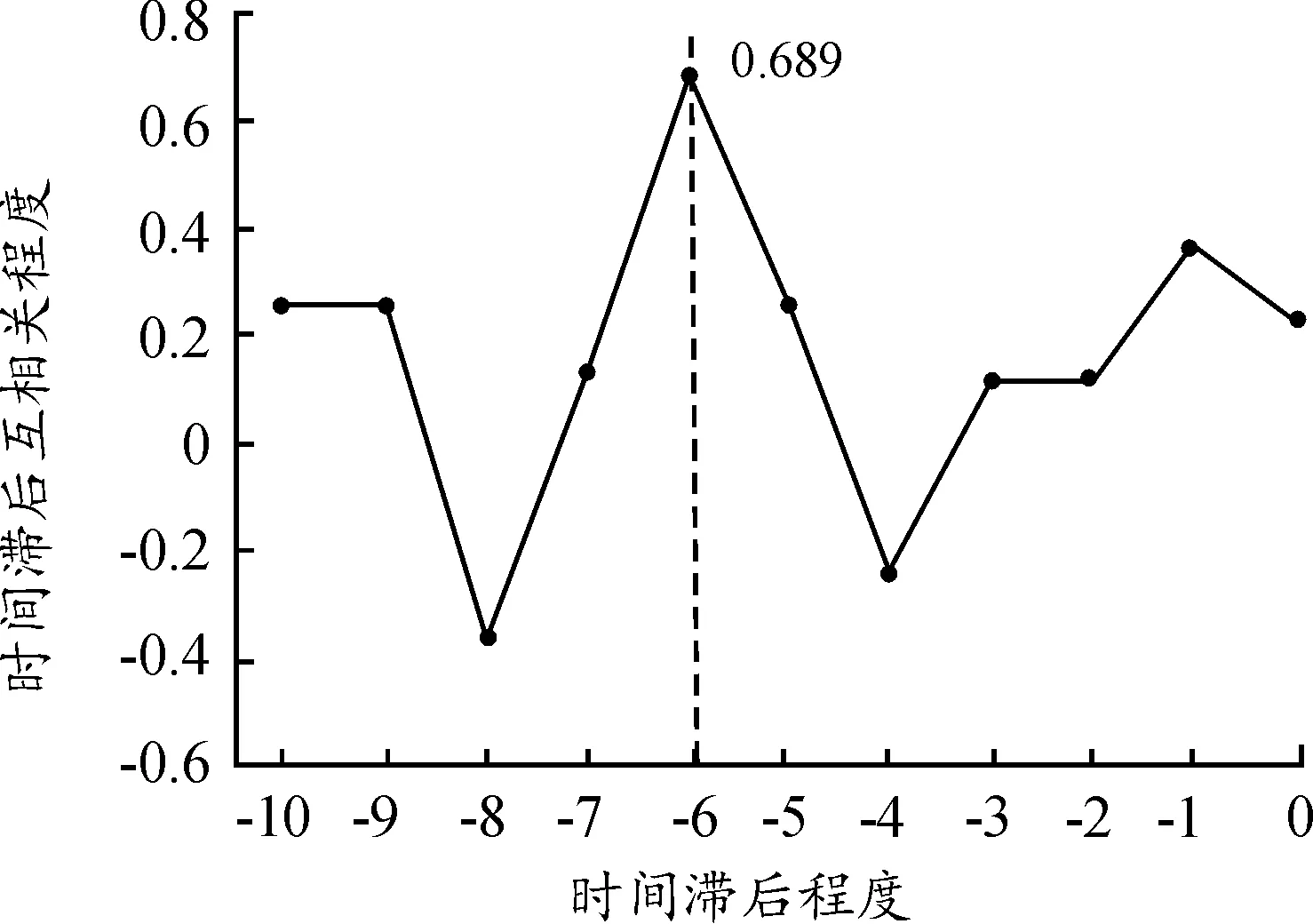
图6 时间滞后互相关曲线
定义7(扩散趋势图):将边集E为拥堵路段因果关系的拥堵路网拓扑结构称为扩散趋势图。
拥堵路网的拓扑结构图描述了拥堵路段之间可能的关系,路段之间的拥堵可能没有必然联系或者相关性较小,因此提出了一个算法用于分析扩散趋势图,如算法1所示。
算法1:扩散趋势图分析算法
输入:各时间点拥堵路段集合,拥堵路网拓扑图邻接表AL。
输出:一组扩散趋势图。
1:Plist← 一个空集合
2:AL← 将AL所有边反向
3: for 节点lanei(i≤n) do
4:Que← 一个空队列
5: 节点lanei入Que队列
6:Graph← 一个空集合
7: whileQue队列非空 do
8: 节点lanex←Que队头出队列
9: 将节点lanex标记为已遍历
10:TempList← 节点lanex的邻接表节点
11: for 节点laney(laney∈TempList) do
12: ifTLCC(Seqx,NSeqy)>Randlanex不在laney节点的邻接表中
13:Graph←Graph∪
14: iflaney未遍历 then
15:Que←Que∪laney
16: end if
17: end if
18: end for
19: end while
20:Plist←Plist∪Graph
21: end for
拥堵路网的拓扑结构图表示的是车流方向,而拥堵扩散的方向应与车流方向相反,因此算法1首先要将邻接表进行反向操作(第2行),即将图中所有边的方向反向。以路段42为例,算法1会筛选符合条件的边(如图7(b)所示),得到的子图即为扩散趋势图,如图7(c)所示。同理可以得到其他路段的拥堵扩散趋势图。
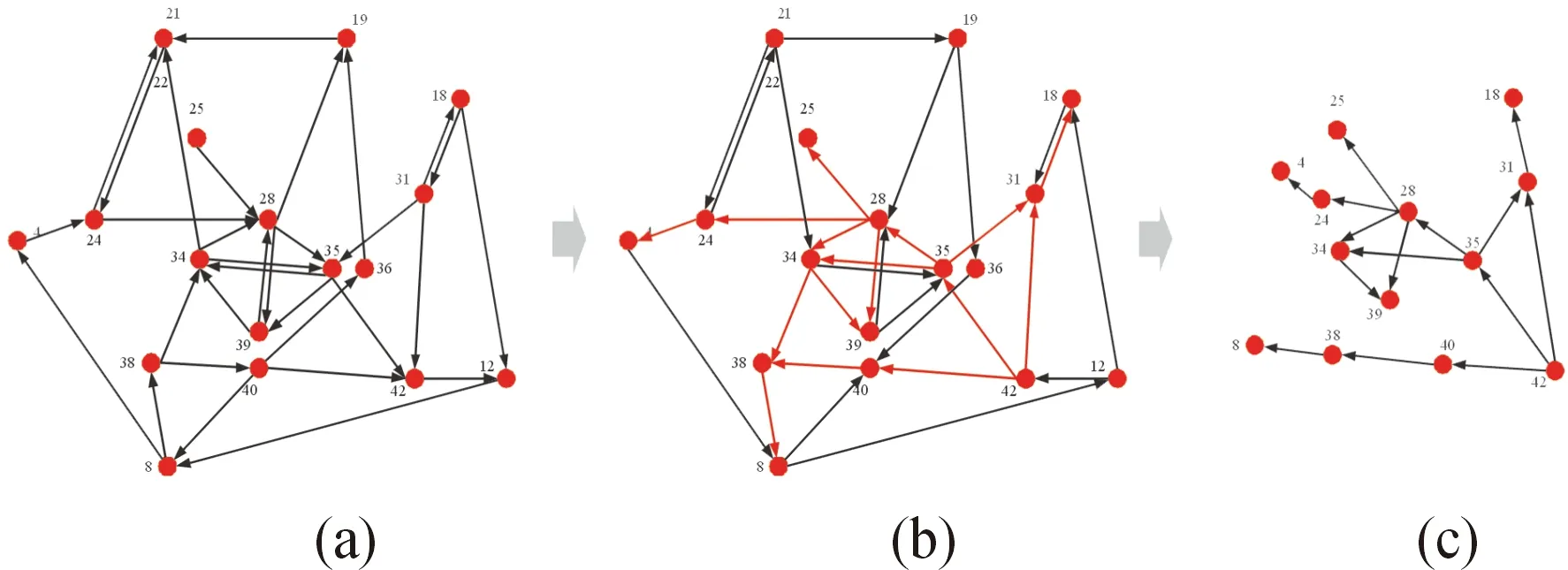
图7 扩散趋势图
2.4 瓶颈识别
城市中各个路段并非是独立的存在,它们彼此相连,互相影响。因此,一条路段发生拥堵后,影响的不仅仅是需要经过该路段的车,对需要经过周围路段的车也有一定的影响。因此,为了保证识别的瓶颈具有更加优越的性能,不仅需要计算拥堵路段自身的拥堵成本,还要分析这些路段的拥堵给周围路段带来的负面影响,即拥堵扩散成本。最终,将拥堵总成本超过阈值的路段作为交通瓶颈。
定义8(路段拥堵总成本):路段总成本为路段自身成本与扩散成本之和,表示为:
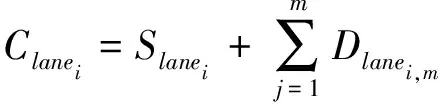
(4)
式中:Slanei表示路段自身拥堵成本,Dlanei表示单个拥堵扩散成本,即向某一条路扩散的成本,m为受拥堵影响路段的总数。
2.4.1自身拥堵程度计算
首先需要计算每条拥堵路段的自身拥堵成本。相同的拥堵程度在不同道路上给城市带来的影响是不一样的,对于市中心和郊区2条拥堵程度一样的路段,计算拥堵成本时不应该得到同样的数值,因为市中心的路段拥堵所带来的经济损失必然高于郊区路段,因此,拥堵程度一样,市中心的路段拥堵成本应该更高才符合实际。通常而言,车流量越大的路段重要性越高,其拥堵造成的损失也越大。因此记录了全时段所有路段的车流量信息,通过路段的平均车流量信息作为描述路段重要程度的指标。道路占用率可以直观地表示路段拥挤程度,将路段的平均车流量信息和平均占用率共同表示其自身拥挤程度。假设路段lanei的平均车流量为αi(辆),道路平均占用率为βi,那么路段lanei的自身拥堵成本表示为:Slanei=αi*βi(辆)。
2.4.2拥堵扩散程度分析
得到路段自身拥堵成本后,需要分析路段拥堵向周围路段扩散的扩散成本。前面的工作已经得到每个拥堵路段的扩散趋势图,如图8(a)所示。图8(b)为扩散趋势图的直观表示,类似于一棵树的结构,如果把节点42看作根节点,每个节点的权值为对应拥堵路段的自身拥堵成本S,边的权重Q为2个节点之间的时间滞后互相关程度,那么节点42的总拥堵成本(扩散趋势图的权重)可以通过图8(b)所展示的方式得到,具体计算方式为:根节点总拥堵成本为路段自身拥堵成本与拥堵扩散成本之和,其中扩散成本为所有子节点权重与边权重乘积之和(见算法2)。同理可以得到所有节点扩散趋势图的权重。

图8 成本计算扩散趋势
算法2:总拥堵成本计算算法
输入:扩散趋势图,节点权值集合S,边权重集合Q。
输出:根节点总拥堵成本。
1: while 图中节点数量 > 1 do
2:nodes← 图中所有出度为0的节点
3:sides← 空集合
4: whilenode(node∈nodes) do
5:sides←sides∪与node连接的边
6: end while
7: while 边side(side∈sides) do
8:tail←side弧尾
9:head←side弧头
10:Dtail←Shead*Qside
11:Stail←Stail+Dtail
12: 删除head、side
13: end while
14: end while
2.4.3瓶颈确定
通过上诉步骤,分别得到了拥堵路段的自身拥堵成本以及扩散成本,两者之和可以共同描述拥堵路段对整个路网的影响,数值越大,表明拥堵对整个路网车辆通行能力影响越大。
城市道路交通瓶颈是路网中对整体路网通行能力影响最大的路段,即瓶颈处的拥堵会严重影响周围区域交通状况,瓶颈处的流量缓解带来的是整体路网通行能力的提升。定义如下。
定义9(城市交通瓶颈):城市交通瓶颈是路网中拥堵总成本超过阈值的路段,分析见式(5):
(5)
式中:flanei=1代表lanei为交通瓶颈;T表示成本阈值。根据式(5),将总成本超过阈值的拥堵路段作为交通瓶颈。
3 模拟与讨论
SUMO是一款开源、微观、多模态的交通仿真软件,可以对每辆车进行单独控制,对于基本数据的获取也相对容易。因此,本文选择SUMO交通模拟器来进行相关实验。首先识别了苏福尔斯路网中的交通瓶颈,并且通过增加车道数来提高车道通行能力,计算了整个路网的平均行驶速度改善百分比。除此之外,比较了现有技术所识别的瓶颈对路网通行能力的改善效果,以此证明所提出的方法具有更加优越的性能。
3.1 瓶颈识别
在本小节中,分别计算了路段自身拥堵成本和扩散成本,确定了苏福尔斯路网中的交通瓶颈。如图9所示,横轴表示路网中所有路段的编号,纵轴表示各路段的拥堵成本。从图中可以看到,基于现有的瓶颈识别技术(仅考虑路段自身的拥堵程度),路段35和37将被识别为苏福尔斯路网的瓶颈。然而,当结合拥堵扩散效应来量化路段的拥堵成本时,路段43和46更有可能被视为瓶颈。特别是与其他路段(如路段35、37和46)相比,路段43自身拥堵程度不是很高,但总拥堵扩散成本却高很多,这是由于路段之间的空间连接,导致路段43上的拥堵往往会蔓延到路段35、37和46。实验结果表明,路网中最拥堵的路段不一定是交通瓶颈,仅根据路段自身的数据去分析交通瓶颈是不严谨的。
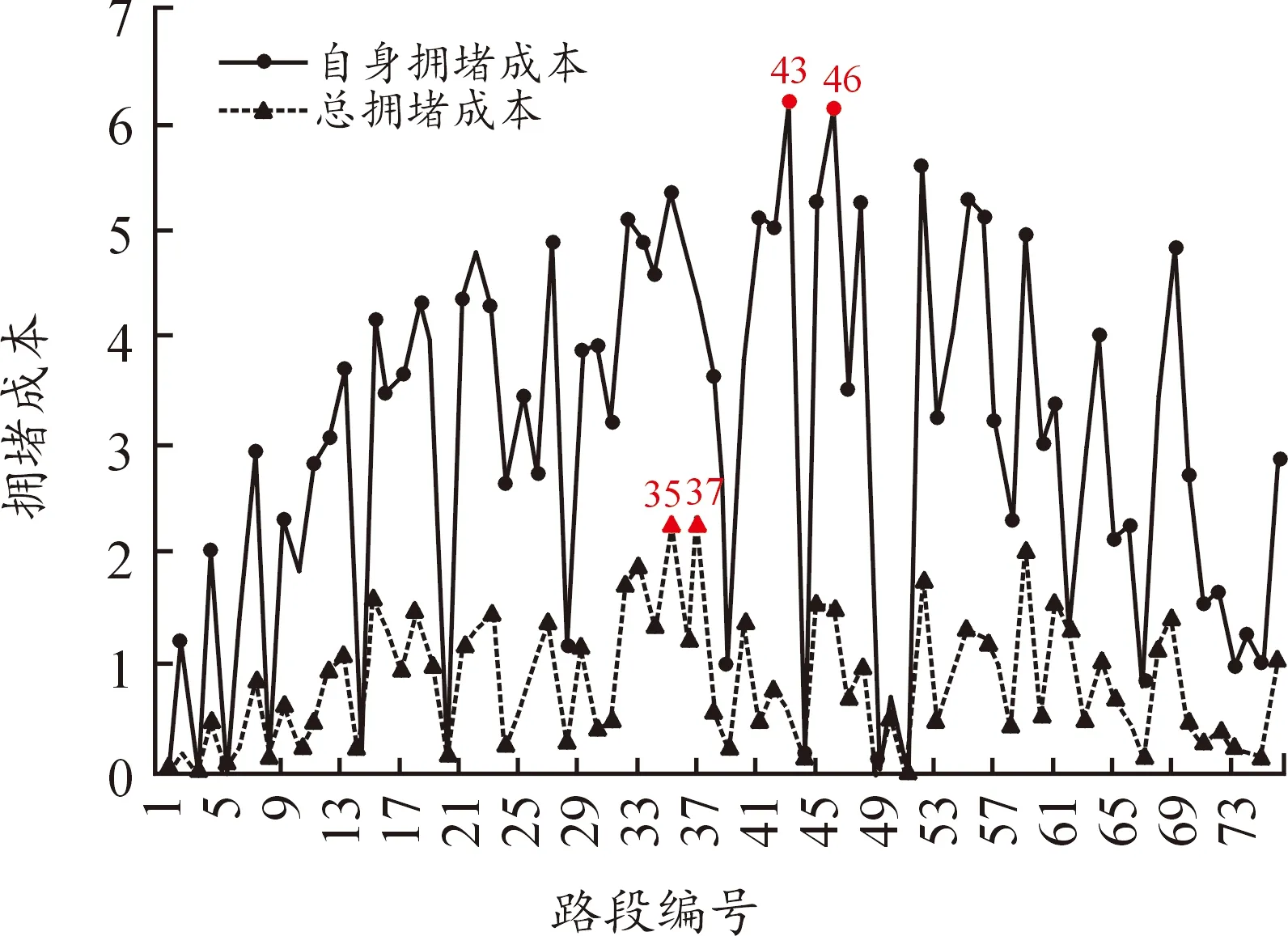
图9 路段拥堵成本曲线
3.2 瓶颈验证
交通瓶颈的直观表达是:瓶颈处的流量缓解带来了显著的路网范围内的流量改善。因此,为了验证本文所提方法在识别交通瓶颈方面的有效性,在SUMO上增加了每个路段的车道数,并分别比较了增加前后路网的车辆通行能力的提高情况。本文通过车辆的出行速度表示路网的车辆通行能力。
如图10所示,路网的通行能力在路段车道数增加后都得到了提高,特别是路段43和路段46,增加车道数后平均行驶速度分别提升了88.1%和92.3%,改善效果远远高于其他路段,说明这2个路段的交通状况会对周围路段产生较大影响。根据定义9可以确定,苏福尔斯路网的交通瓶颈为路段43和路段46。结果表明,提出的同时考虑自身拥堵成本和扩散成本的瓶颈识别方法可以更好地捕捉城市道路交通瓶颈,在城市道路交通路网的瓶颈识别方面具有优越的性能。
3.3 实验结果对比
在本小节中,分别在不同瓶颈识别技术识别的瓶颈处增加车道数,按方法分类,比较了在不同车辆到达率下的路网的车辆通行能力,结果如图11所示。可以看到,当车辆到达率较小时,几种方法识别的瓶颈对路网通行能力的改善效果相差无几,因为这时路网的容量还没有饱和,换言之,路网本身就不是很拥堵,增加车道后自然对拥堵缓解不明显。当车辆到达率逐渐增大,路网的拥堵开始加重,这时不同瓶颈识别技术的优劣便体现了出来。从图11中可以看出,当车辆到达率为每小时5 400辆车时,在识别的瓶颈处增加车道数所带来的交通改善收益远高于其他方法,路网平均行驶速度提高了90.6%,说明提出的考虑拥堵扩散的瓶颈识别方法可以更有效地捕捉城市交通瓶颈,能够最大程度地缓解交通拥堵。

图10 行驶速度改善的百分比曲线
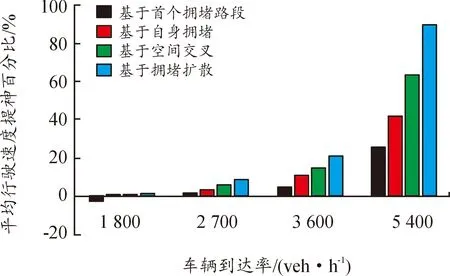
图11 行驶速度改善的百分比柱状图
4 实际场景应用实验
4.1 应用场景介绍
本次采集的数据来自四川省绵阳市,通过路边摄像头对车辆信息采集,将采集的数据通过算法进行轨迹还原,从而得到本文所需要的原始数据集。数据集包含路网数据和车辆数据,其中路网数据包含288条路段以及97个交叉路口,车辆数据包含 100 000辆车的轨迹路线。将数据集在SUMO仿真平台上运行,记录各个时刻的道路占用率以及指定时间范围内道路的车流量信息,这样可以得到本文算法需要的初始数据。通过分析这些数据,使用本文所提出的技术实现交通瓶颈识别。
4.2 因果关系分析
在本文中,通过道路车道占用率以及车辆停滞比例来确定道路的拥堵状态。根据绵阳市交通具体情况,路段拥堵阈值M、N分别设置为70和50。实际生活场景中,路段拥堵状态改变后会维持一段时间,不会立即又发生改变。因此,为了同时考虑数据的有效性和整个算法的计算效率,采用时间片段来收集数据,结合当地实际情况,最终以15 s为一个时间片段,收集各时间点路网中路段的拥堵状态。如图12所示,统计了各时间点拥堵路段的数量,从图中可以得到,前面2 h整个路网基本没有发生拥堵,之后拥堵路段数量开始增加,严重时有43条主干道发生拥堵。在10 h后拥堵情况没有继续恶化,拥堵路段数量开始缓慢减少,第19 h后路网基本没有拥堵。
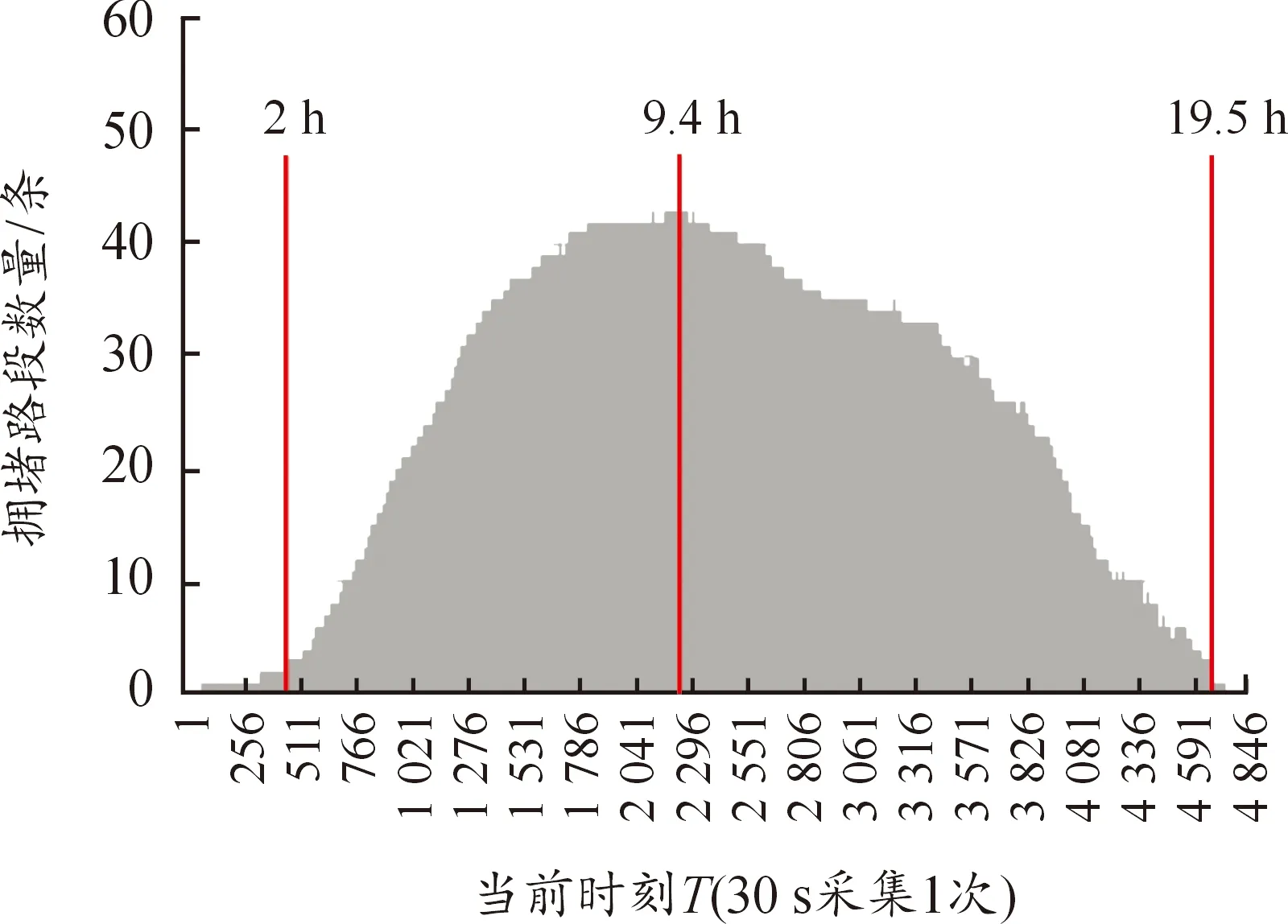
图12 各时间点拥堵路段数量
在分析拥堵路网拓扑结构图时,如果2个拥堵路段距离过远,就可以认为这2个路段的拥堵不存在因果关系。首先获取了路网中所有路段的长度,按照长度对路段排序,剔除其中长度过长或过短的路段,计算剩余路段的平均长度,最终以平均长度的4倍作为本文算法的距离阈值,如图13所示。时间滞后相关程度可以确定2个路段的拥堵互相影响的程度,结合表2中关于相关系数强度的阐述,将时间滞后相关程度大于0.3的2个拥堵路段视为拥有因果关系。
4.3 扩散趋势识别
在本小节中,通过算法1分析出拥堵路段的扩散趋势图。为了方便起见,从每个拥堵路网拓扑结构图中给出其中一个扩散趋势图。如图14所示,从图中可以看出,路网中有三片区域发生了严重拥堵,其中路段19的扩散趋势图最大,拥堵向西北方向扩散,从而导致大片区域发生拥堵。

图13 路段长度
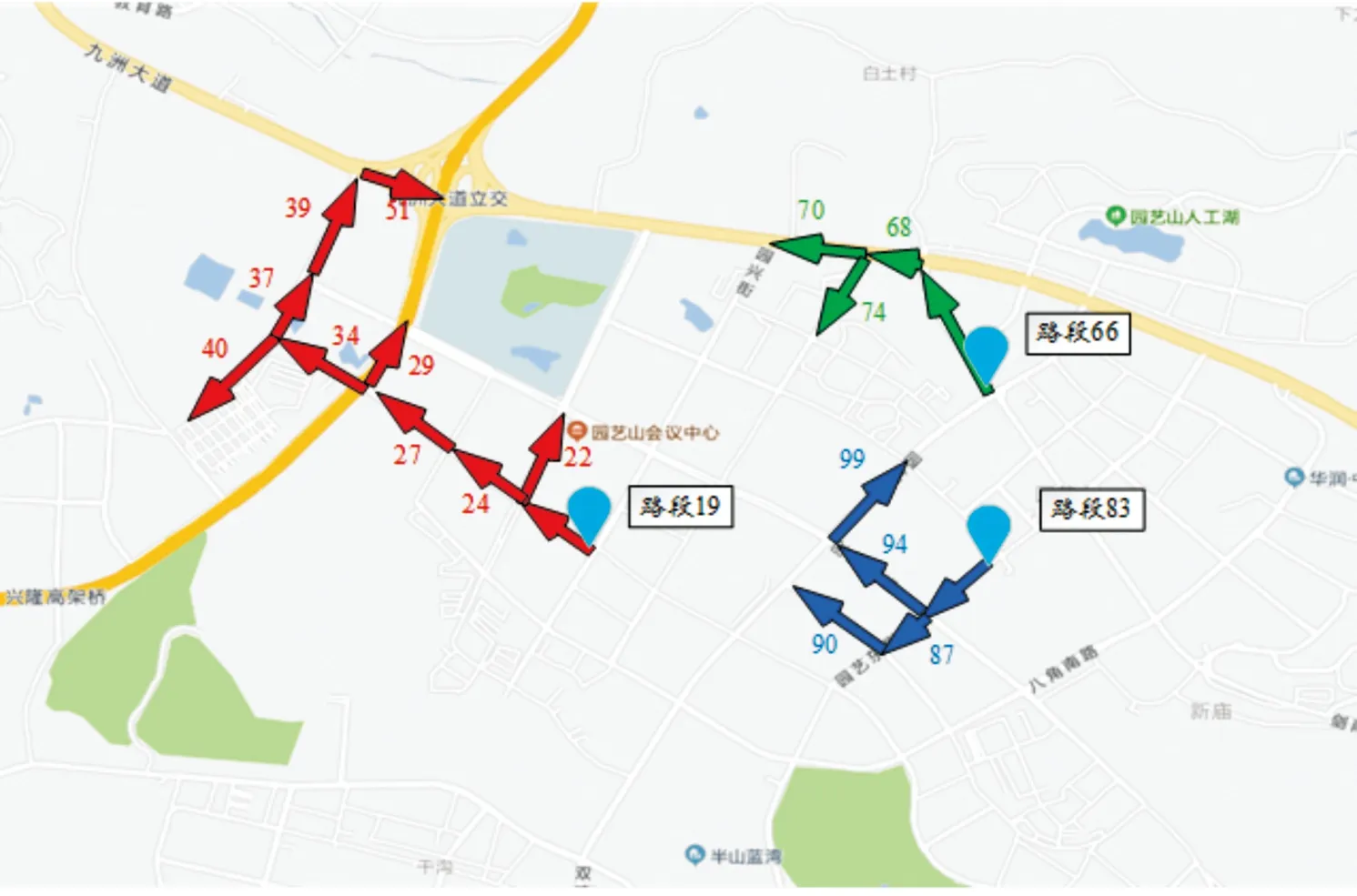
图14 扩散趋势图
4.4 瓶颈识别与优化
4.4.1瓶颈识别
得到每个拥堵路段的自身拥堵成本和扩散成本,两者之和视为绵阳市路网中各路段的总拥堵成本,将总拥堵成本超过阈值的路段作为该拥堵区域的交通瓶颈。图15为其中一个扩散趋势图的计算结果,从图中可以发现,某些路段(例如路段19)的拥堵程度不如其他路段(例如路段22、34、37和39)高,但它们的拥堵扩散效应显著,缓解这些路段的拥堵可以使整个路网车辆通行能力显著提升。因此,这些路段才应被视为路网的瓶颈。

图15 路段拥堵成本
4.4.2瓶颈优化
如果能够有效缓解交通瓶颈处的流量,那么整个城市交通路网的拥堵就可以显著缓解。在本文模拟实验中通过增加交通瓶颈处车道数量使得瓶颈处拥堵减少,但在实际生活中,通过增加基础设施来缓解拥堵并不常见,更多的是优化交通信号灯。因此,手动将交通瓶颈处的信号灯做一定优化,使得瓶颈处的拥堵能够得到有效缓解,并且对比了优化前后整个路网中车辆平均行驶速度,如图16所示。通过计算,优化后车辆平均行驶速度相较于优化前提升了94%。
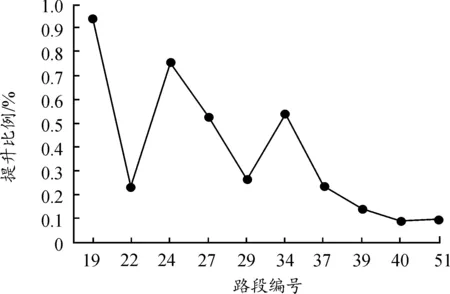
图16 交通状况改善效果
5 结论
为解决城市交通网络中的瓶颈,提出了一种新的城市交通瓶颈定义,该定义计算路段的拥堵成本,同时考虑了道路自身拥堵成本和扩散成本。首先从车道占用率以及车辆停滞比例对路段拥堵作了阐述,得到路网中的拥堵路段,并进一步分析出拥堵路网拓扑结构图。其次给出了2条拥堵路段因果分析的方法,得到拥堵路段扩散趋势图。然后根据平均交通流量和平均占用率计算了道路自身拥堵成本,根据扩散趋势图得到路段的扩散成本。此外,利用道路自身拥堵成本和扩散成本,计算了不同路段的总拥堵成本,并确定了城市道路交通网络中的交通瓶颈。最后,通过SUMO交通仿真软件进行了模拟实验,并进一步在实际生活场景中验证。结果表明,所识别的交通瓶颈在城市地区能够表现更加优越的性能,特别是在路网容量比较饱和时优势更加明显。
