混合动力汽车双行星排齿轮机构啮合特性分析及优化
2022-10-12吴盛斌李雨涵
谭 伟,吴盛斌,李雨涵
(重庆理工大学 汽车零部件先进制造技术教育部重点实验室, 重庆 400054)
0 引言
行星齿轮机构具有结构紧凑、承载能力强、传动比大等优点,广泛应用于汽车动力传动系统中。相较于定轴齿轮传动系统,其复杂的结构对制造和装配的要求更高。由于制造安装误差、轴承间隙及轮齿承载变形等都无法避免,这些不利因素将影响行星齿轮机构的啮合特性,影响动力传动系统的NVH性能,甚至缩短其使用寿命。相关研究表明,传动误差幅值和轮齿接触载荷变化是齿轮系统振动噪声的主要激励源[1-3]。齿轮修形是一种经济实用的齿轮优化方法,可有效减小传动误差波动、改善齿轮啮合性能,从而减小振动噪声[4]。
Tavakoli等[5]采用解析法研究了齿廓修形参数对静态传动误差的影响,并以传动误差波动量最小为优化目标,获得了最佳齿轮修形参数。Ohno等[6]基于斜齿轮三维有限元模型,分析了修形量对齿轮接触应力的影响,并确定了斜齿轮的最佳修形量。Pramono[7]通过实验研究了齿廓修形对直齿圆柱齿轮动态时域和频域特性的影响。蒋进科等[8]对斜齿轮系统进行LTCA分析,基于啮合副的承载变形、啮合刚度及啮合力得到最佳修形齿面,改善了齿轮的啮合性能,增大了齿轮的重合度。封旗旗等[9]采用齿廓修形和偏心螺旋线修形改善了差速器齿轮机构的振动噪声特性,并通过有限元和实验验证了齿轮修形对齿轮疲劳寿命的影响在允许范围内。
上述研究表明,齿轮修形方面的研究多数针对单啮合齿轮,对行星齿轮系统的齿轮修形研究还比较少,特别是混合动力汽车动力传动系统中广泛采用的双行星排齿轮机构。鉴于此,本文建立考虑行星架结构柔性的双行星排齿轮机构刚柔耦合动力学模型,分析其在纯电动工况下的啮合特性,并根据分析结果确定齿轮修形范围,在此基础上,以传动误差最小、啮合错位量最小及齿面载荷分布为优化目标,采用遗传算法得出最佳齿轮修形方案,并通过仿真实验验证了修形方案的可行性。
1 模型建立及啮合特性分析
1.1 双行星排齿轮机构模型建立
本文的研究对象为混合动力耦合系统内的双行星排齿轮机构,包含2个发动机输入轴、2个电机输入轴和2个输出轴,构型如图1所示。其各部件的连接方式为:发动机输入轴与PG1行星架连接,MG1输入轴与PG1太阳轮连接,MG2输入轴与PG2太阳轮相连,PG1齿圈与PG2行星架及输出轴相连,PG2齿圈固定在壳体上。

图1 双行星排构型示意图
行星齿轮机构齿轮的宏观设计参数见表1所示。

表1 行星齿轮机构宏观设计参数
结合轴系等零部件的结构参数,建立包含各轴系、行星架、行星销轴及各类轴承的双行星排齿轮机构模型,考虑到行星架在传动时变形量大,对齿轮机构的动力学性能有较大影响,因此在所建模型基础上,导入行星架的网格模型,对其进行缩聚以替换原模型的行星架,最终在Romax软件中建立了考虑行星架结构柔性的刚柔耦合动力学模型如图2所示。

图2 双行星排齿轮机构动力学模型示意图
1.2 啮合特性分析
行星齿轮啮合过程中,行星齿轮P和太阳轮S组成外啮合副(SP啮合副),行星齿轮P与齿圈R组成内啮合副(RP啮合副)。本文研究的双行星排齿轮机构搭载于城市公交客车的混合动力耦合系统上,考虑到纯电驱动可满足多数运行工况,且城市公交客车的运行路线固定,传动系统在循环工况下工作,因此本文以纯电驱动工况为例,分析研究不同输入扭矩对行星齿轮机构啮合特性的影响。
1.2.1啮合错位量
啮合错位量指齿轮啮合副传动时两轮齿的分离程度,主要由齿轮制造误差,装配误差及结构柔性变形等决定。通常规定沿齿轮啮合副局部坐标系Z轴正方向两齿面分离度变大时,啮合错位量为正,反之为负[10-12]。行星齿轮系统啮合副多、行星架变形不规律,导致各啮合副错位量的大小及方向较其他齿轮系统更加复杂。图3为后行星排内外啮合副在不同驱动转矩下的啮合错位量。
结合行星齿轮结构特点及仿真结果可知,行星架在Z轴方向的弯曲变形使啮合副产生了不同方向的啮合错位量,且内外啮合副的啮合错位量绝对值与MG2输入扭矩呈正相关。在输入扭矩为100 N·m时,内外啮合副错位量绝对值都小于10 μm,但增大到大扭矩600 N·m时,内外啮合副的最大错位量分别达到了38.1 μm和32.2 μm,不利于齿轮系的正常传动,有必要对齿轮系进行优化以改善其啮合错位量对载荷变化的敏感性。

图3 载荷对啮合错位量的影响
1.2.2传动误差
理想工作状态下,可将齿轮啮合副看作2个圆柱体在无相对滑动的状态下进行传动,传动速比为两简化圆柱体半径的比值。但在实际传动中,由于制造安装误差及受载变形等因素的存在,齿面无法正常啮合,从动轮的瞬时转角不等于理论转角,从而产生传动误差(transmission error,TE)。工程上将其定义为沿啮合线方向上从动轮齿廓实际啮合位置同理想条件下所处理论位置之间的偏差[13-14]。
图4为后行星排各啮合副在不同扭矩输入工况下的传动误差,可以看出,扭矩增大会使传动误差变大,在小扭矩工况下,内外啮合副的传动误差较小,但在大扭矩600 N·m工况下,内外啮合副的传动误差幅值分别为3 μm和2.13 μm,其中,后排行星轮2与齿圈构成的啮合副的传动误差不随扭矩增大而改变,与啮合错位量分析结果相同。

图4 载荷对传动误差的影响
1.2.3齿面载荷分布
图5为后排各啮合副在输入扭矩为500 N·m工况下的齿面载荷分布情况,其中RP1-5代表齿圈与行星齿轮1-5组成的内啮合副,SP1-5表示太阳轮与行星轮1-5组成的外啮合副。
从图5可知,后排各齿轮啮合副都存在严重的偏载现象,且各啮合副的最大载荷出现位置与上文分析的啮合错位量方向相反,验证了齿面载荷分布和啮合错位量方向之间的相关性。
根据分析结果可知,载荷变化对齿轮啮合错位量及传动误差的影响较大,且齿轮在传动过程中都出现了严重的偏载现象。为降低啮合错位量及传动误差对载荷变化的敏感性,并使齿面载荷均匀分布在齿面中部,有必要对行星齿轮机构进行优化。

图5 后排齿轮啮合副接触斑分布情况
2 齿轮修形方案研究
2.1 齿轮修形技术
齿轮修形技术指在齿轮齿面上适当去除材料,以减小制造安装误差、轴承间隙及齿轮承载变形等所带来的不利影响,获得均匀的齿面载荷分布及降低齿轮传动误差,是改善齿轮啮合特性,提高承载能力和延长使用寿命的经济有效的方法[15]。
2.1.1齿向修形
齿向修形指沿着齿宽方向休整轮齿表面,以减小齿轮啮合错位量、消除偏载现象从而改善齿轮机构承载能力,主要有齿向鼓形修形及齿向斜度修形2种方式。
将齿面两端对称去除齿面材料,中间鼓起的方法为齿向鼓形修形,如图6所示,该方法可使轮齿在齿宽方向的中部位置相切,以实现最大接触载荷出现在齿面中部的目的。

图6 齿向鼓形修形示意图
当有效接触齿宽ba小于实际齿宽b时,齿向鼓形量Cα的计算公式为
(1)
式中:Ft为分度圆上的圆周力;Δs为啮合错位量;b为齿轮齿宽;Kγ为综合啮合刚度,由下式求得
Kγ=(0.25+0.75εα)KthKMKRKBcosβ
(2)
式中:εα为端面重合度;Kth为单齿理论啮合刚度;KM为修正系数;KR为齿廓系数;KB为基准齿条系数;β为螺旋角。
齿向斜度修形指在齿宽方向按一定斜率去除齿面材料,可理解为微调齿轮螺旋角,其能够有效消除齿轮的偏载现象,齿向斜度修形量Cβ通过下式求得
(3)
2.1.2齿廓修形
齿廓修形指根据需要去除齿廓方向上产生啮合干涉的部分材料,以降低齿轮啮入、啮出冲击影响,改善齿轮传动的平稳性[16-17]。考虑到在一对啮合副中,一个齿轮齿顶修形与另一齿轮齿根修形的作用相同,为保证修形后的强度,本文仅考虑齿顶修形,其修形示意图如图7所示。

图7 齿廓修形示意图
齿廓修形由齿廓鼓形量、修形长度和修形曲线决定,本文采用H.Sigg[18]提出的齿廓修形方法,最大鼓形量为
(4)
修形长度由修形曲线的终始点决定,其优化作用体现在啮合副啮入啮出阶段,因此本文以啮合副双齿啮合起点到单齿啮合起点之间的啮合线长度来定义齿廓修形长度。
L=Pb(εα-1)
(5)
式中,Pb为基圆节距。
修形曲线为齿廓修形量从0增大至Δmax所形成的曲线,工程上一般采用二次抛物线作为修形曲线。
(6)
式中,Δ为x处的修形量大小;x为啮合位置的相对坐标,可理解为修形曲线上不同位置对应的修形长度。
2.2 基于遗传算法的齿轮修形参数研究
2.2.1修形参数优化设计
齿轮修形寻优方面,传统的齿轮修形需要经验丰富的工作人员进行大量的参数调试与计算,费时费力,并且在优化目标较多时,很难找到最优的齿轮修形方案。鉴于此,本文以传动误差一阶谐波分量最小、啮合和错位量最小及齿面载荷分布为优化目标,将不同修形方式的修形量作为自变量,采用遗传算法求得最佳齿轮修形组合,设计的遗传算法运算过程见图8。其种群规模为100,变异概率为0.2,交叉概率为化0.6,种群进化代数为300。
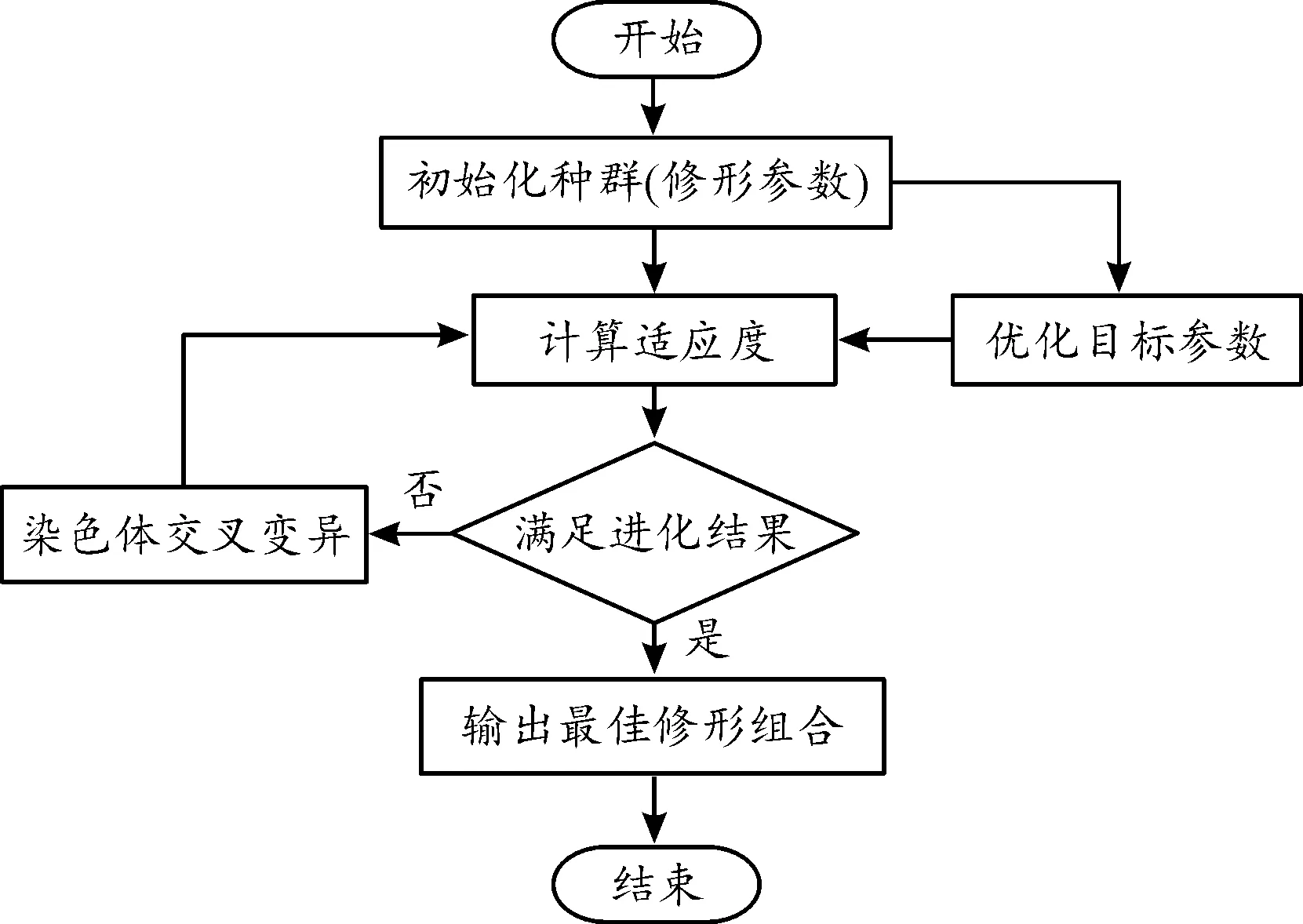
图8 齿轮修形参数优化过程
2.2.2齿轮修形参数范围确定
为定义优化样本数据范围,需要确定各齿轮修形量的范围,根据齿轮修形理论可知,齿轮承受的载荷越大,需要的齿轮修形量也就越大,所以只需计算输入扭矩最大时各齿轮修形量的大小即可。本文以输入扭矩600 N·m为最大扭矩展开研究,结合上文给出的齿轮修形量计算公式和齿轮啮合特性分析结果,求得各齿轮副修形量的样本数据范围如表2所示。

表2 遗传算法样本数据范围 μm
本文基于传动误差、啮合错位量及齿面载荷分布所构建的目标函数如下。
TE∑=k1TE1+…+knTEn
(7)
μ∑=k1μ1+…+knμn
(8)
F∑=k1F1+…+knFn
(9)
式中:TEn、μn和Fn分别为本文所研究的不同工况下的传动误差、啮合错位量和齿面最大载荷;kn为不同工况下的权重系数,kn=1,根据上文研究可知n≤6,n∈N*。

(10)
2.2.3齿轮修形参数优化结果
图9为SP1啮合副传动误差一阶谐波与太阳轮齿向鼓形量和齿齿廓鼓形量的关系图,可以看出:当齿向鼓形量为4~6 μm、齿廓鼓形量为8~10 μm时,传动误差一阶谐波趋于收敛,此时对应的结果即为最佳修形量。

图9 传动误差一阶谐波收敛图
图10为遗传算法产生的1 000种备选齿轮修形方案,根据各方案适应度值的大小判断修形方案的优劣,适应度值越小,修形方案越好。

图10 备选方案适应度结果
基于遗传算法求得的最优齿轮修形组合出现在第974个备选方案,对应的适应度值为17.775,其各齿轮修形量如表3所示。

表3 最佳齿轮修形组合 μm
3 优化方案验证
根据上文得到的齿轮修形组合对行星齿轮机构进行为微观参数优化,此处以后行星排齿轮啮合副为对象,分析齿轮修形优化方案对齿轮啮合特性的影响。
由图11可知,齿轮修形优化后的各齿轮副的啮合错位量随载荷的变化趋势与修形前相同,但不同工况下的啮合错位量幅值相较于修行前均有所降低,这是由于修形组合的齿向斜度修形剔除了啮合错位量反方向的齿面材料,抵消部分啮合错位量的原因。
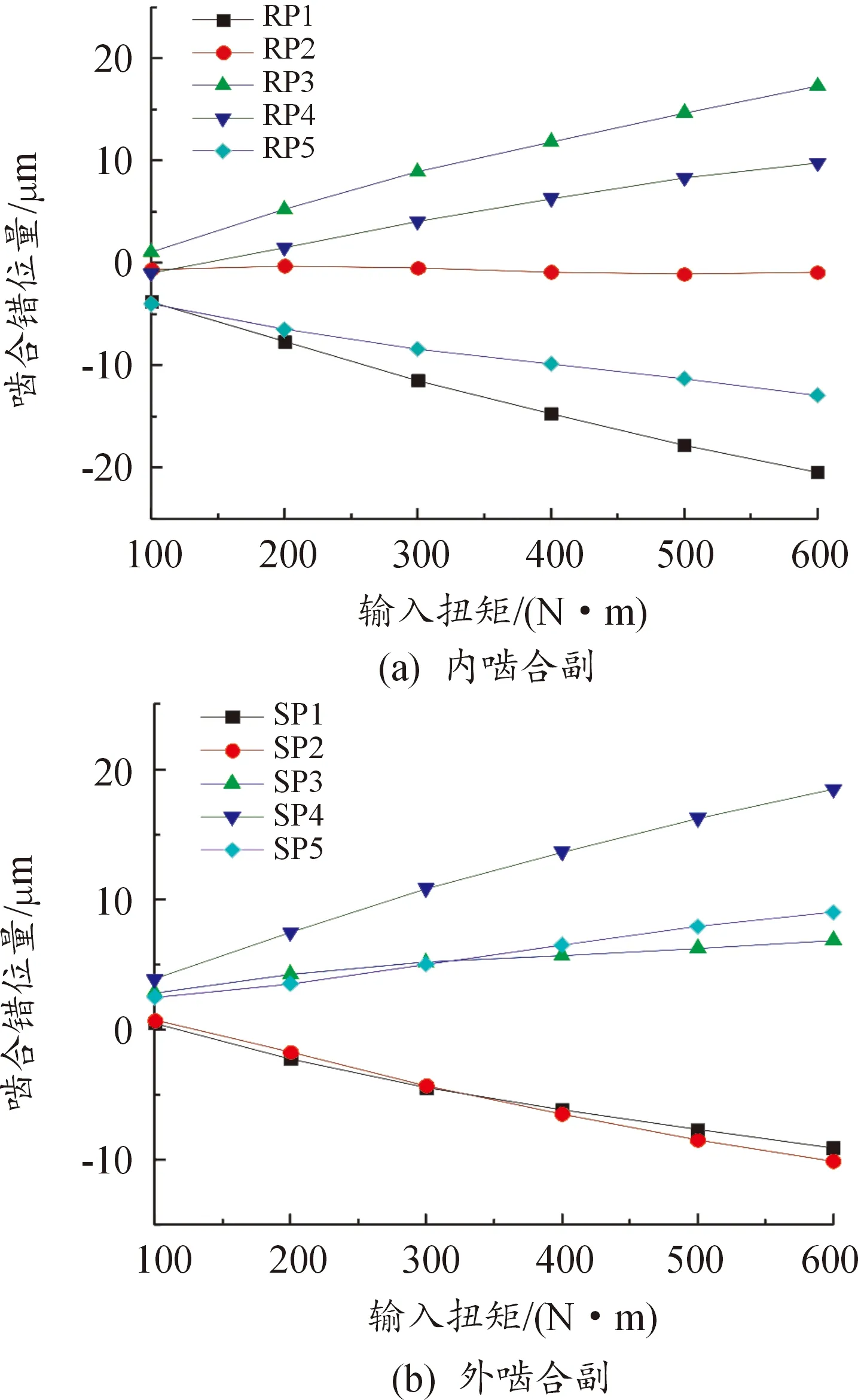
图11 优化后的啮合错位量
以SP1啮合副为例,其在不同工况下的优化结果如表4所示,可以看出,从输入扭矩为 200 N·m开始,齿轮修形方案对啮合错位量的优化力度随载荷增大而增大,有效避免了在大载荷工况下出现大的啮合错位量。

表4 啮合错位量优化力度
根据图12可知,不同载荷下,后行星排内外啮合副的传动误差幅值都在[0,1]内波动,不与载荷变化呈现相关性,说明齿轮修形方案有效避免了传动误差对载荷变化的敏感性,体现了优化方案的先进性。
由图13可知,齿轮修形优化后的齿面最大载荷并未出现在齿轮中部位置,仍存在一定程度的偏载现象,这是由于在求解最优齿轮修形方案时,综合考虑了啮合错位量、传动误差和齿面载荷分布原因。相较于图5所示的接触斑结果,齿轮修形方案有效避免了优化前齿轮啮合副的边缘载荷,改善了齿面载荷分布,主要是因为齿向鼓形修形去除了优化前齿向方向上产生边缘载荷处的齿面材料,使轮齿啮合位置偏向齿面中部的原因。

图12 优化后的传动误差

图13 优化后的齿面载荷分布
齿轮齿面的最大载荷决定着齿轮的使用寿命,对齿轮的啮合特性也有较大影响。以后排太阳轮与各行星轮构成的啮合副为例,其在输入扭矩为500 N·m时,齿轮优化方案对齿面载荷的影响如表5所示。可以看出,优化后的齿面最大载荷相较于优化前均有所降低,且对SP4啮合副出现的最大载荷的优化力度最大,达到了31.1%。优化方案使得各行星齿轮啮合副间的最大载荷差值减小,载荷分配更加合理,减小了某一啮合副相较于其他啮合副过早损坏的概率。

表5 齿面载荷优化力度
4 结语
本文以某混合动力汽车搭载的双行星排齿轮机构为研究对象,在Romax软件中建立刚柔耦合动力学仿真模型,研究纯电动工况下,不同输入转矩对啮合特性的影响。在此基础上,采用遗传算法,以啮合错位量、传动误差和齿面载荷分布为优化目标,求得最佳齿轮修形方案,对行星齿轮机构进行微观参数优化。根据优化结果可知,相较于优化前:
1) 啮合错位量均有所降低,且大载荷工况下,优化力度更大,在输入扭矩为600 N·m时,优化力度达到了40.2%,有效降低了啮合错位量对载荷变化的敏感度;
2) 各个工况下传动误差都在[0,1]内波动,不与载荷变化成相关性,使行星齿轮机构在各工况下的平稳性增强;
3) 消除了啮合副的边缘载荷,减小了各啮合副的齿面最大载荷,使传动扭矩在各行星齿轮啮合副间的分配更合理。上述结论说明了本文齿轮修形方案的合理性和先进性。
