转频调制下齿轮泵压力脉动机理

2022-10-12许文纲王志颖孙闯严如强陈雪峰

航空学报 2022年9期

许文纲,王志颖,孙闯,严如强,陈雪峰

西安交通大学机械工程学院,西安 710049

航空发动机作为飞机的“心脏”、动力之源,是一种集结构、材料、制造、液压、气压、热工、电子、控制等众多尖端技术于一身并运行于高转速、高温、重载、强扰动等极端服役环境下的高科技、高附加值的高精密复杂机械产品,被誉为现代工业“皇冠上的钻石”,是中国航空工业的瓶颈,严重制约着中国军用、民用先进飞机的发展。燃油控制系统被誉为发动机的“心脏”,其中主燃油泵是燃油控制系统的核心元件,重要性不言而喻。据统计1986—2004年间发生的387起燃油控制系统故障中,主燃油泵发生故障高达66起,其中54起液压管路故障也是由主燃油泵故障引起的,因此对主燃油泵性能进行研究具有重要意义。齿轮泵作为主燃油泵的重要组成部分,因其结构紧凑、体积小、重量轻、价格低廉,对油液污染敏感度低,自吸性能好而广泛应用于电力、汽车、冶金、军工、航空、航天和化工等各个机械行业,同时也有自身的缺点比如：齿轮所受的径向压力不平衡、轴承容易磨损、流量均匀性差、压力脉动大、振动大、噪声大等。国内外学者针对齿轮泵压力脉动从机理、齿轮泵结构参数优化、软件仿真、实验等方面进行了大量的研究。柏宇星等采用流场分析软件CFX对齿轮油泵内部流场进行三维非定常计算,通过设置监测点,得到不同位置的压力脉动结果,实验表明主动齿轮齿腔压力脉动要高于从动齿轮,齿频是影响压力脉动的主要因素。张鑫用AMESim软件建立了齿轮泵的功能模型,并仿真得到压力脉动数据,然后用神经网络计算得到的脉动数据与仿真得到的数据进行比较。陈中华等利用平稳小波分解与重构将压力信号的低频波动项与高频脉动项进行了分离, 并对低频波动和高频脉动部分的功率谱进行了分析,得到工频可作为齿轮磨损故障的特征频率,对轮齿磨损做出诊断。阿巴沙分析了压力脉动机理,运用外啮合齿轮泵错相位并联方法和外啮合齿轮泵闭环伺服控制方法来减小脉动。喻开清通过研究齿轮泵流量脉动机理的数学模型,得到了齿轮各参数对流量脉动的影响,并通过遗传算法优化齿轮泵参数以达到减小流量脉动的目的。Mancò和Nervegna建立了齿轮泵准稳态数学模型的微分方程。该模型在预测出口压力脉动方面取得了良好的效果。Mucchi和Dalpiaz提出通过比较实验结果与仿真结果来研究齿轮泵的振动特性,其中对原有模型的进、出口控制体进行修正,得到了齿轮泵进、出口压力的脉动。随后,Mucchi等在考虑齿轮泵进口、出口压力脉动的基础上,建立了啮合区域非牛顿流体的湍流模型,得到了更加精确的压力脉动模型。Tian设计了一个与密闭死腔容积相连的减压室来吸收压力脉动,以代替传统的卸荷槽,表明减压室能够衰减95%的压力脉动峰值。Rituraj等研究了齿轮泵加工制造过程中锥度和同心度对齿轮泵容积效率和出口流量脉动的影响。Mhana和Popov研究表明非对称齿轮泵的压力脉动变化相比对称齿轮泵更加平稳,压力突变最大发生在进油口第1个密闭齿腔。Frosina等用PumpLinx建立了齿轮泵的三维流体动力学模型,考虑了所有的泄漏。仿真和实验在压力脉动幅值和周期上都得到了较好的一致性,同时表明出口压力越大,压力脉动幅值越大。Rituraj等针对齿轮泵叶尖泄漏提出了一种适合大范围工况的快速集中参数方法,模型中考虑了进口压降和湍流影响,通过HYGESim软件仿真得到压力脉动的变化。Mancò和Nervegna提出一种新型的测量技术,通过安装在驱动齿轮上的压力传感器来检测外部齿轮泵齿间压力随时间的变化。实验中首次证实了在进口侧啮合叶片内压力峰值的出现,在进口侧齿轮脱离时齿腔内存在空化现象。Cinar等采用实验验证与理论分析相结合的方法研究齿轮泵密闭腔中压力大小的分布,从泵的进口到出口分别在壳体等间隔布置了4个传感器来测量每个腔中压力的变化,比较精确地预测了齿轮泵转动过程中压力的变化情况。

流体的脉动流动主要分为2种类型：① 流道几何形状呈周期性变化；② 流体的速度或流动方向呈周期性变化。齿轮泵出口脉动的产生既有出口控制体形状的周期性变化,又有流体速度方向的周期性变化。旋转过程中轮齿对出口流场产生扰动,最终形成湍流流动。本文第1节给出了齿轮泵产生压力脉动的机理,转频、齿频及齿频的倍频分量是压力脉动主要组成部分；第2节采用谱方法给出了齿轮泵出口测点处压力脉动的表达式,研究了齿轮泵转频对齿频及倍频的调制作用；第3节分析了齿轮泵压力脉动的影响因素及工程应用展望；第4节给出结论。

1 齿轮泵压力脉动模型

采用欧拉法建立齿轮泵每转过一个齿时产生的压力脉动方程,首先选择控制体,如图1所示将齿轮泵流体域分成4类控制体,分别是等体积控制体Ⅰ(即由轮齿、轴承座、壳体组成)、进口控制体Ⅱ、出口控制体Ⅲ和密闭死腔控制体Ⅳ,齿轮旋转过程中控制体个数是周期性变化的。根据连续性方程,假设液体在控制体中的流动是稳态流动、且绝热等熵,得到每个控制体中的压力与转角的关系为

(1)

式中：为油液的体积模量；为控制体体积；为齿轮转动角速度；Δ为控制体中油液流量的变化量。

图1 齿轮泵流体域中不同的控制体Fig.1 Fluid domain in gear pump segregated into different control volumes

1.1 控制体中的连续方程

1.1.1 等体积控制体

规定控制体中流量的变化量为流入和流出控制体的流量之差,流量在控制体中的传递如图2所示。

Δ=-

(2)

式中：为流入控制体的流量；为流出控制体的流量。

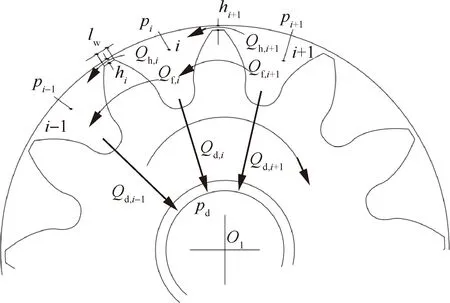
图2 第i个密闭齿腔体积流量Fig.2 Volumetric flow rates for isolated tooth space i

齿轮泵齿顶间隙、齿侧间隙处液体的流动为平板间的库埃特-泊肃叶流动。

(3)

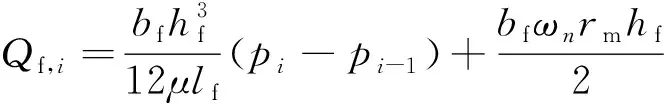
(4)

式中：h,为通过齿顶间隙从第个控制体流入到第-1个控制体的流量；f,为通过齿侧间隙从第个控制体流入第-1个控制体的流量；为第个控制体的压力；、分别为第个控制体齿顶间隙和齿侧间隙；、分别为齿轮的齿宽和齿高(=1,2分别表示主、从动齿轮)；、分别为齿顶圆半径和齿高一半处对应的半径；、分别为齿轮齿顶厚度和齿轮节圆处的厚度；为油液黏度；为齿轮的角速度。

控制体与轴承座孔通过侧向间隙相连,为平面泊肃叶流动。

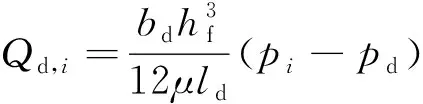
(5)

式中：d,为通过齿侧间隙从第个控制体流入轴承座孔的流量；为0.5倍的齿根圆齿距；为齿根圆到轴承座孔的径向距离；为轴承座孔中油液压力。

联立式(1)～式(5)可得等体积控制体的连续方程：

(6)

式中：为第个控制体的体积。

在等体积控制体中压力可表示为

(),())

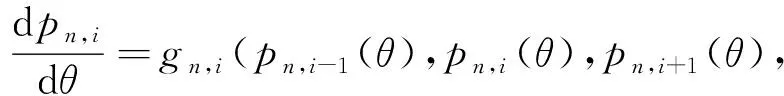
(7)

式中：主动齿轮侧=1,=1,2,…,;从动齿轮侧=2,=1,2,…,;、表示主、从动齿轮等体积控制体最大个数；,为等体积控制体压力脉动的隐函数表达式；()、()分别表示进口、出口控制体压力。

1.1.2 进口和出口控制体

齿轮泵进口分别跟液压油箱、主从动齿轮形成的第1个密闭腔、轴承座孔、双齿啮合区形成的密闭死腔、卸荷槽相连；齿轮泵出口分别与工作负载、主从动齿轮形成的最后1个密闭腔、双齿啮合区形成的密闭死腔、卸荷槽相连。

齿轮泵进口通过端面间隙分别与密闭死腔(压力)和轴承座孔相连,液体传输近似为平面流动,密闭死腔只存在于双齿啮合区；与油箱(压力)和卸荷槽相连的部分,因形状和尺寸的变化,液体输送等效为湍流模型。

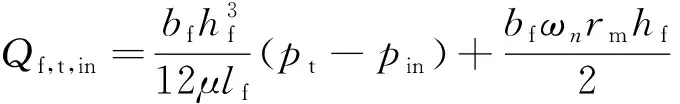
(8)

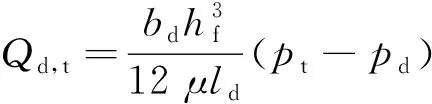
(9)

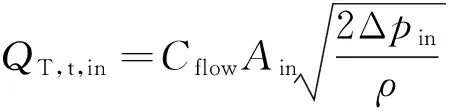
(10)

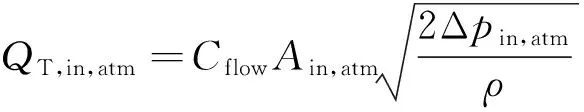
(11)

式中：为齿轮泵进口与密闭死腔的体积流量；为密闭死腔与轴承座孔的体积流量；为齿轮泵进口与卸荷槽相连时的体积流量；为齿轮泵进口与油箱的体积流量；为卸荷槽与泵进口连接时的流道截面积；为泵进口与油箱连接的流道截面积；=065为湍流系数；Δ=-,Δ=-,为进口控制体压力；为油液密度。

联立式(1)、式(3)～式(5)、式(8)～式(11)可得进口控制体的连续方程：

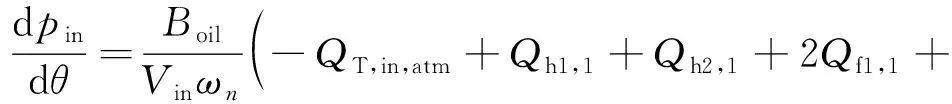
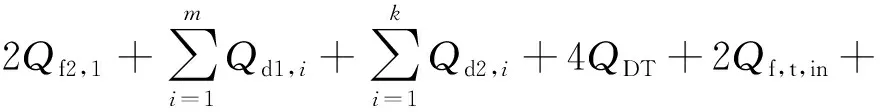
(12)

式中：为齿轮泵进口控制体体积；、分别为主、从动齿轮第1个控制体通过侧隙流入进口的流量；、分别为主、从动齿轮第1个控制体通过径向间隙流入进口的流量；d1,、d2,分别为主、从动齿轮轴承座流入进口控制体的体积流量；表示密闭死腔控制体流入进口控制体的体积流量。

齿轮泵出口压力由负载大小决定,流体传递过程按湍流处理；齿轮泵出口通过齿侧间隙与主、从动齿轮密闭腔和密闭死腔相连,流体传递设定为平面流动。

(13)

(14)

=(2π)

(15)

式中：为齿轮泵出口与密闭死腔之间的体积流量；为齿轮泵出口与卸荷槽之间的体积流量；为齿轮泵出口与负载之间的体积流量；为体积容量；为卸荷槽与泵出口连接时的流道截面积；Δ=-,为出口控制体压力信号的高频成分。

联立式(1)、式(3)、式(4)、式(13)～式(15)可得出口控制体的连续方程：

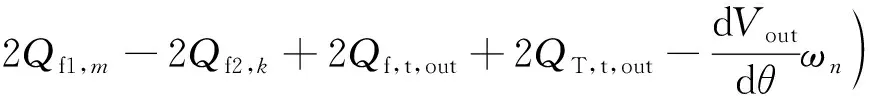
(16)

式中：为齿轮泵出口控制体体积；f1,、f2,分别为主、从动齿轮第、个控制体通过侧隙流入进口的流量；h1,、h2,分别为主、从动齿轮第、个控制体通过径向间隙流向进口的流量。

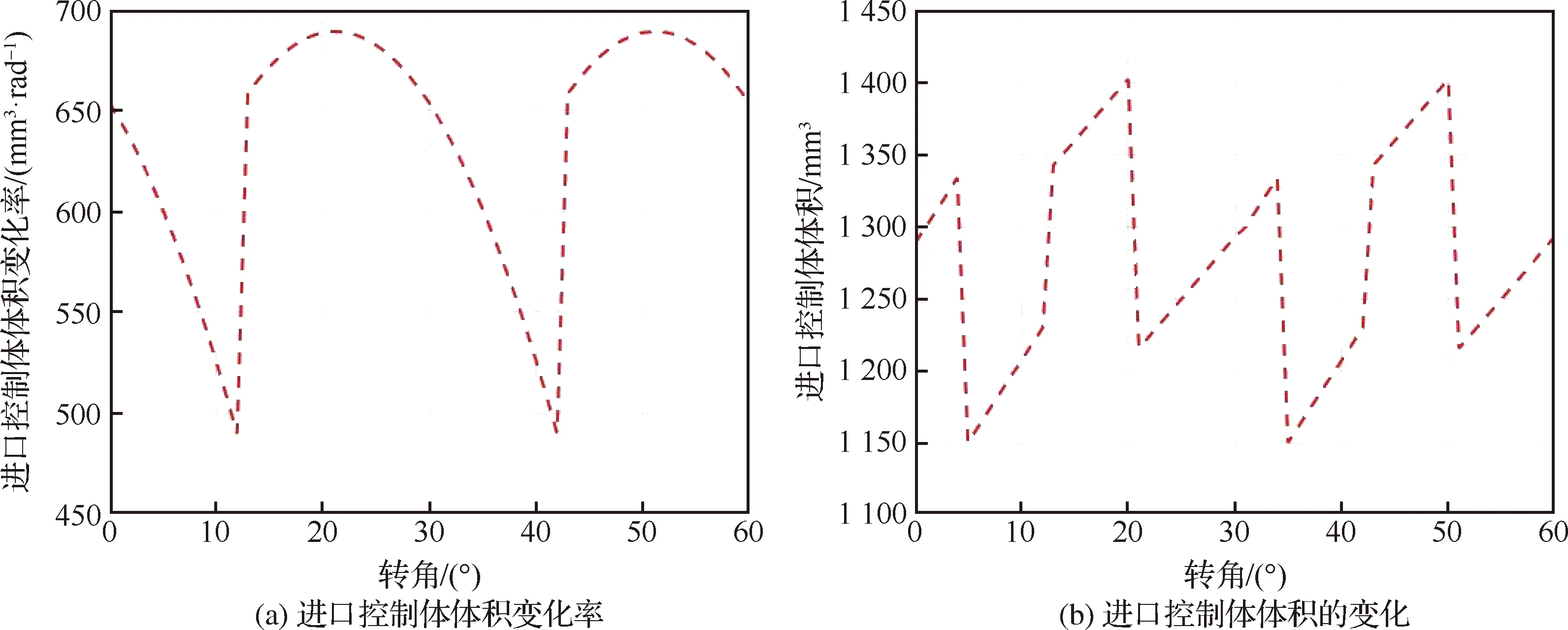
进、出口控制体体积随齿轮转角而变化,与齿轮单双齿啮合有关,实验中齿轮泵进、出口控制体的体积和变化率如图3所示,齿轮泵有12个齿,以30°为一个周期进行变化,其中体积的突变点表示有齿腔突然与进出口控制体连通或断开,进、出口控制体中压力变化可表示为

(17)

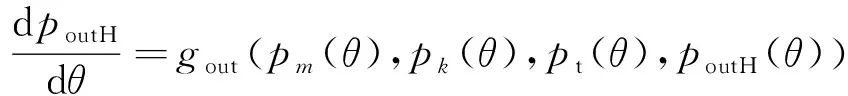
(18)

式中：和分别为进口、出口压力脉动的隐函数表达式；()、()分别为主、从动齿轮第、个控制体的压力。

1.1.3 密闭死腔控制体

齿轮泵密闭死腔只在双齿啮合时存在,防止密闭死腔产生过高的压力,在齿轮两侧挡板上开了对称的卸荷槽；当密闭死腔减小,压力增高时高压侧的卸荷槽接通,当密闭死腔增大,压力减小时,低压侧的卸荷槽接通,卸荷槽接通和断开的时间与齿轮泵本身的结构有关。

联立式(1)、式(8)～式(10)、式(13)、式(14)可得密闭死腔控制体的连续方程：

(19)

式中：为密闭死腔控制体体积。

密闭死腔控制体体积的变化与两对齿轮啮合点的位置有关,实验中齿轮泵密闭死腔控制体的体积和变化率如图4所示,表明每30°周期内只有双齿啮合段0～10.73°内存在密闭腔,密闭死腔控制体压力可表示为

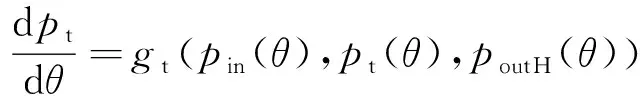
(20)

式中：为密闭死腔压力脉动的隐函数表达式。

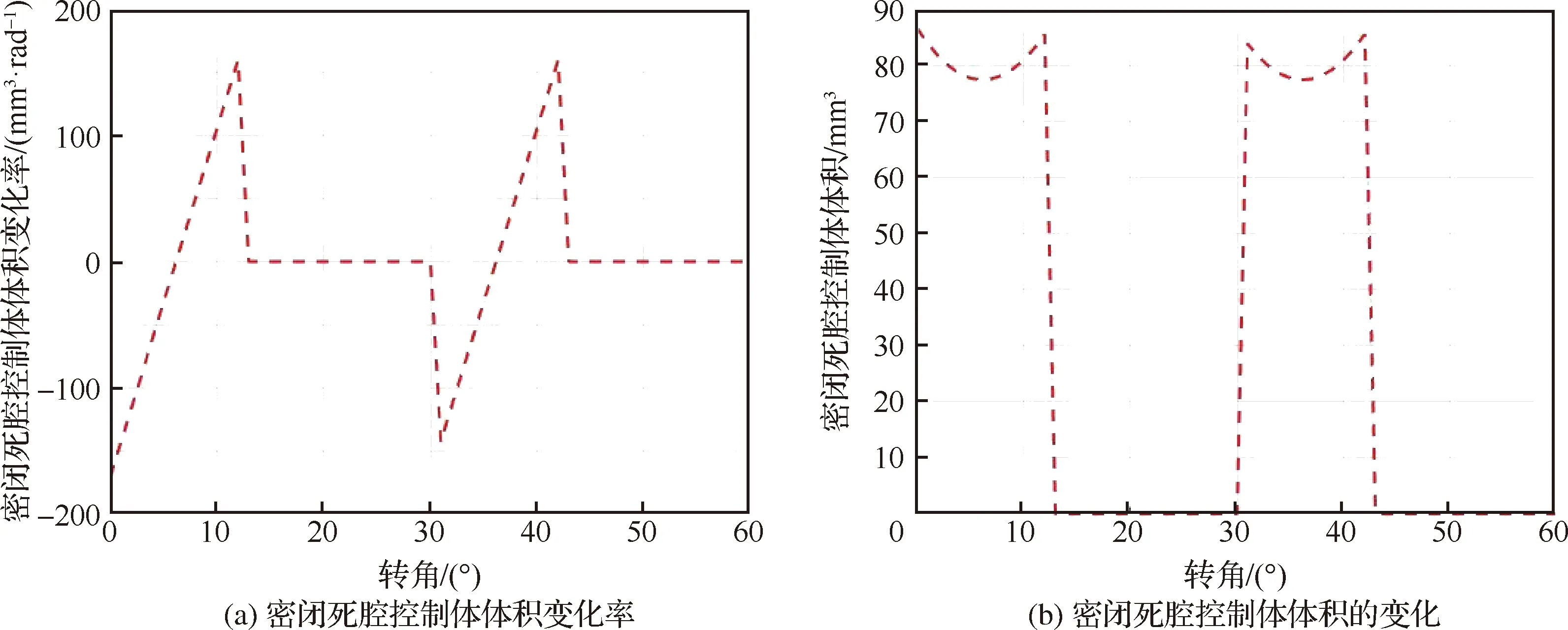
图4 齿轮泵密闭死腔控制体的体积和变化率Fig.4 Volume and rate of change of gear pump trapped control volume

1.2 齿轮泵压力脉动方程

式(7)给出了任意一个密闭齿腔的压力随转角的变化,将式(7)应用于主动齿轮侧的个密封腔和从动齿轮侧的个密封腔得到等体积控制体的方程组,再联合式(17)、式(18)、式(20)得到齿轮泵转过一个齿时各控制体的压力脉动微分方程组。

(21)

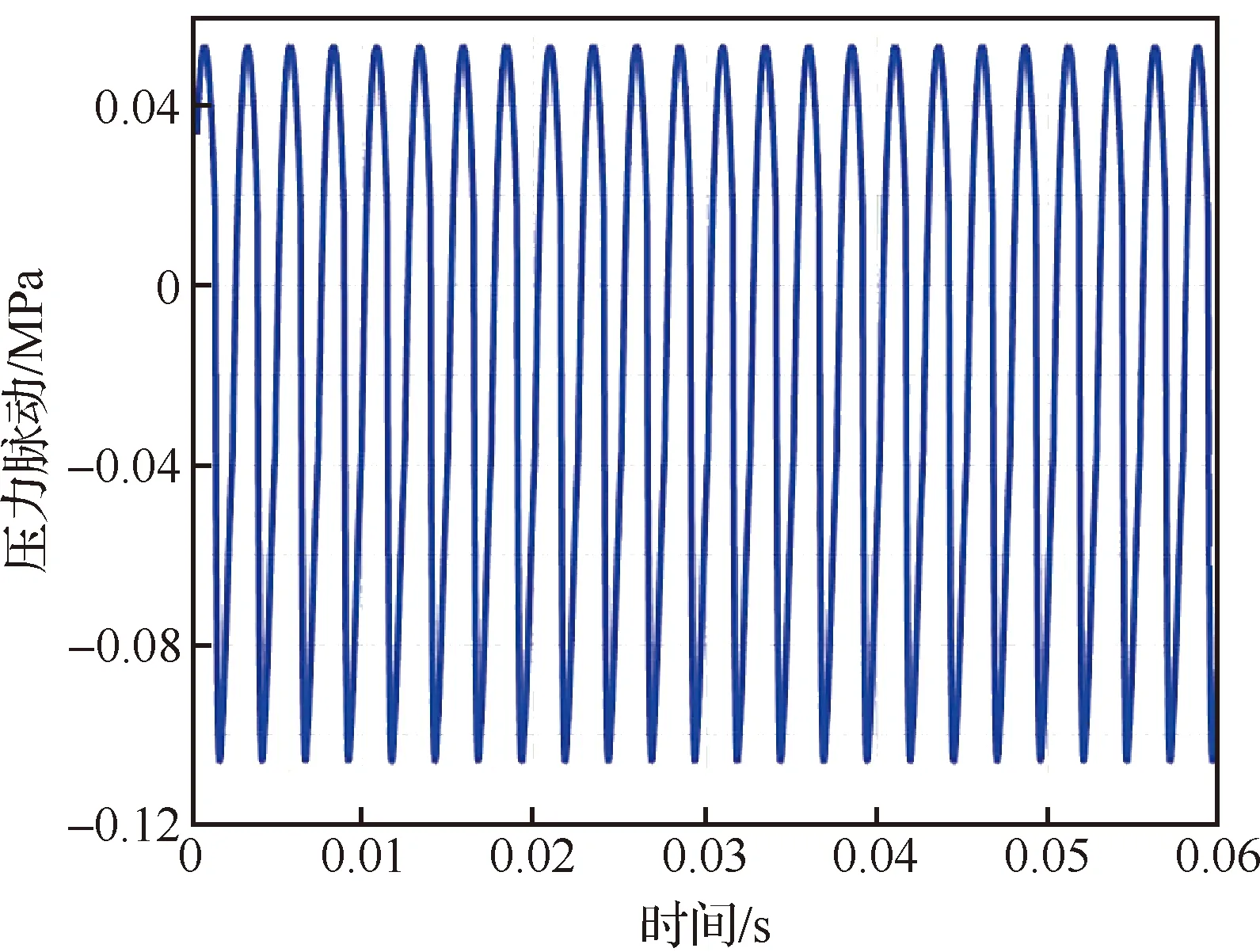
求解式(21)的初值由实验确定,齿轮转过一个齿的时间段内,根据齿轮的具体结构参数确定方程组的个数和每个方程组内方程的个数,往往无法用一个方程组来完整表达一个周期。以2 500 r/min,负载压力5 MPa为例,得到齿轮泵出口的压力脉动如图5所示。由图可知齿轮泵出口压力脉动是周期信号,主要频率为500 Hz(齿频),记单齿啮合产生的压力脉动信号为()。该模型主要揭示了齿轮泵产生压力脉动的机理,即主要因为齿轮泵周期性运动,导致各控制体体积呈周期性变化,假设各控制体为刚性体,液压油不可压缩,则齿轮泵内部流场呈周期性变化,因而出口压力呈周期性脉动。虽然该模型揭示了压力脉动信号主要组成分量(转频、齿频及倍频)之间的线性叠加作用,但是没考虑分量间的非线性作用(即转频对齿频及倍频的调制作用),因而,不能全面地展示压力脉动包含的信息,第2节在第1节的基础上从湍流结构组成和能量传递角度研究转频分量对其他分量的调制作用。

2 齿轮泵出口测点处压力脉动模型

齿轮泵依靠轮齿啮合产生的体积变化来吸入和排出流体,传动过程中有双齿啮合区域会形成密闭腔,随着密闭腔体积减小压力逐渐增大,当压力大于出口压力时,密闭腔中的流体通过间隙流向出口管路,伴随着漩涡流的产生,因而流场由层流转变为湍流。Antoniak和Stryczek对齿轮泵流场进行可视化研究,设定了2种不同的操作参数进行对比实验,均发现齿轮泵出口流场有湍流出现,在非标准条件(即较高转速(1000±10) r/min、进口负压(-0.05±0.005) MPa、较高温度(50±2) ℃、出口高压(3±0.01) MPa)下出现了明显的空化泡沫和气泡群,同时加剧了湍流强度。因此,齿轮泵出口流场中不可避免地会出现湍流现象,属于壁湍流,但是湍流强度受外界操作参数和齿轮泵自身结构的影响,如齿轮泵内部开设对称的卸荷槽,一定程度上减少了射流的产生,降低了湍流强度。

湍流流动是一种高度非线性的复杂流动,迄今为止,仍然没有一个可以完整解释并描述湍流的定义。人们对湍流的“定义”也只是通过对湍流运动的特征进行综合列举。其中,湍流的特征主要包括：不规则性、扩散性、耗散性、连续性、间歇性、记忆特性等。因此无论是提出新理论还是建立工程计算模型都需要用实验加以确证；另一方面,实验本身能发现湍流的新现象,进而提出新理论和模型。

湍流实验是人们最先认识湍流的工具。1883年雷诺通过有色流体流动实验观察到层流到湍流的整个流动变化过程,这一方法成为最早研究湍流的流动显示法,该方法能直观得到流体运动情况,但不能对流体流动进行定量分析。20世纪30年代,热线风速仪(HWA)应用到湍流测量中,得到流动的脉动速度,进一步发展了湍流理论,为湍流实验研究提供了有效的手段。20世纪80年代初,粒子图像测速仪(PIV)通过粒子成像测量流体速度,可以得到流体流动的速度场和温度场。到20世纪90年代,人们发明了多普勒全场测速技术(DGV),该方法改进了激光多普勒测速仪(LDV)只能单点测量的缺点,可以测量空间的三维速度,适用于测量高速大流场流体流动。简单的湍流问题通常可以理论分析近似求解,而实际存在的复杂湍流流动主要通过实验和数值模拟研究。随着计算机技术的发展,人们通过某些数值方法对湍流进行模拟,取得与实际比较吻合的结果,常用的数值模拟方法有直接数值模拟、大涡模拟、统计平均法和Reynolds平均法等。其中Reynolds平均法是目前使用最为广泛的湍流数值模拟方法。根据对Reynolds应力作出的假定或处理方式不同,常用的湍流模型有两大类：Reynolds应力模型和涡黏模型。其中Reynolds应力模型分为Reynolds应力方程模型和代数应力方程模型；涡黏模型分为零方程模型、一方程模型和两方程模型。工程中使用最为广泛的是两方程模型,最基本的两方程模型是标准-模型,即分别引入关于湍动能和耗散率的方程。本文采用理论分析和实验验证来研究齿轮泵出口测点处的压力脉动。实验中测量压力脉动的高频压力传感器安装在齿轮泵出口的圆管上,如图6所示。

图6 高频压力传感器安装位置Fig.6 Installation location of high frequency pressure sensor

2.1 不可压缩均匀各向同性湍流的动力学模型

2.1.1 基本方程

齿轮泵出口湍流结构比较复杂,但是向下游运动过程中,由于没有外界干扰,逐渐演化成各向同性湍流。假设油液是不可压缩的,则在测量点附近形成不可压缩的均匀湍流,对于不可压缩流体的均匀湍流场,它的平均速度是常向量,可以令平均速度为0。均匀湍流的脉动场满足Navier-Stokes方程。

运动方程：

(22)

连续方程：

(23)

式中：为方向上的速度；为流体密度；为流体的运动黏性系数。

齿轮泵出口测点处的脉动压力满足Poisson方程,在无界的均匀湍流场中,Poisson方程的Green函数为1,于是脉动压强的解析积分表达式为

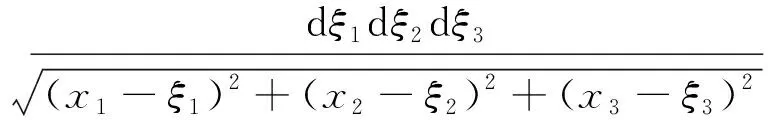
(24)

式中：(,)为空间处时刻的压力；、、为3个坐标轴方向的相对位移；、、为压力作用点在3个坐标轴方向的坐标。

理论上,给定脉动方程速度场的初始条件,根据均匀湍流的基本方程可以解出均匀湍流场的一个样本流动。然而,湍流场是随机过程,要获得湍流的全部信息,必须给出足够多的独立初始场,然后进行统计分析。

不可压缩均匀湍流场中的湍动能和雷诺应力分别为

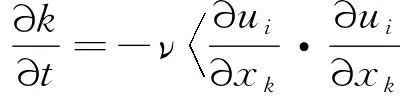
(25)

(26)

由式(25)可知,均匀湍流场中湍动能总是衰减的,因此在均匀湍流流动过程中,湍流可能近似的演化为各向同性。

2.1.2 谱分析

均匀湍流是空间上的平稳过程,并且在相关距离很大时,各阶相关函数都等于零。这种平稳随机过程,随机脉动可以用傅里叶级数展开。根据均匀湍流的谱理论,将均匀湍流在足够大的三维空间上作傅里叶级数展开,复数形式表示为

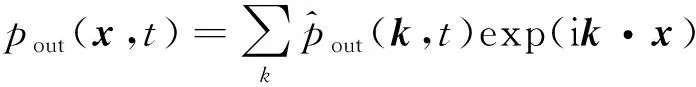
(27)

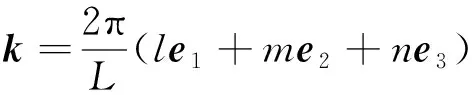
(28)

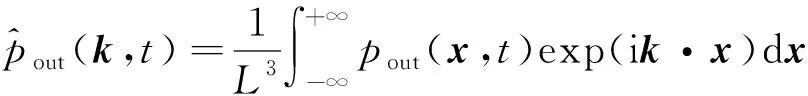
(29)

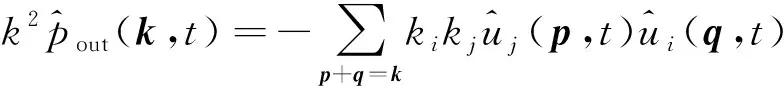
(30)

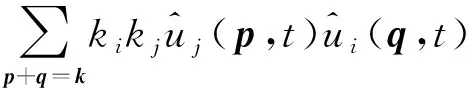
一旦得到湍流脉动的压力谱在谱空间上的分布,将其代入式(27)就可以得到物理空间的湍流脉动。研究表明“壁湍流”中无论是近壁缓冲区小尺度结构还是对数区的大尺度结构,动力学上均能不相互依赖、自维持地演化,然而实际的湍流场中存在强烈的尺度间的非线性相互作用,特别是当雷诺数升高时,不同区域、不同尺度相干结构之间的相互作用也会增强。Hutchins和Marusic利用湍流边界层实验数据,采用傅里叶分解的方法分离出对数区流向尺度大于边界层厚度的大尺度运动信号,他们发现,这些外区大尺度运动可以深入到近壁区,使得近壁平行于壁面的流向脉动速度分量也包含大尺度的能量,并且这部分来自大尺度的能量随着雷诺数的升高而增大,而小尺度的速度脉动能量几乎不变。这一效应也被称为外区大尺度运动对近壁湍流的叠加效应。同时,Mathis等发现在外区大尺度低速条带对应区域内,近壁小尺度速度脉动较弱,而在大尺度高速条带对应区域,近壁小尺度速度脉动较强,这一效应被称为幅值调制效应。因此,湍流的各尺度分量之间存在线性叠加和非线性的调制作用。

实验中齿轮泵出口高频压力传感器是基于压电效应的点测量,得到的脉动信号是一维标量,因此采用周期信号来代替这种平稳随机信号。齿轮泵旋转过程中相对于齿轮的啮合频率,齿轮的转频则要低得多。由于质量偏心、安装不对中、轴弯曲等原因将导致出现转频的低次谐波,如转频的1倍频、2倍频、3倍频等,因此转频产生的压力脉动信号傅里叶展开式为

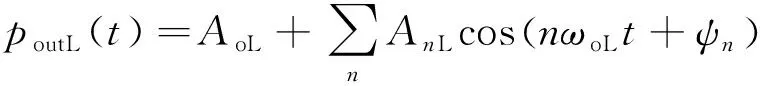
=1,2,…,6

(31)

式中：为直流分量；cos(+)为转频的基波分量,为转频,为相位角；≥2时,Lcos(+)为转频的谐波分量,为相位角。

由于齿轮泵齿腔压力从进油口到出油口依次增大,主、从动齿轮都会向进油口方向偏斜,这使得转频产生的低次谐波分量非常微弱,可忽略,因此式(31)可近似写为

()=+cos(+)

(32)

式中：、为傅里叶系数。

齿轮泵中每对齿轮的啮合为一个小周期(即齿频),而在齿轮泵转一周过程中有12对齿轮交替进行啮合形成一个大周期(即转频),在一个啮合周期内,啮合的齿轮发生了进入啮合、脱离啮合、单双齿啮合等多次刚度和控制体体积突变的过程,因此在齿轮泵的压力脉动信号中必然还包含了齿频的高次谐波成分。齿轮泵转动过程中,齿轮泵的负载和转速变化会引起频谱的谐波分量的调制,负载的变化会引起压力脉动信号的幅值调制,而转速的变化会引起相位调制,幅值和相位调制同时进行。调制导致与齿频相关的边频分量增加,因此,在以齿频为载波频率的两侧包含了以2个转频为调制频率的边频带。

假设转频引起的幅值调制信号为

′()=′cos()

(33)

转频引起的相位调制信号为

″()=″sin()

(34)

式中：′为调幅信号幅值；″为调频信号幅值。

联立式(21)、式(33)、式(34)得到的脉动信号()的傅里叶展开可表示为

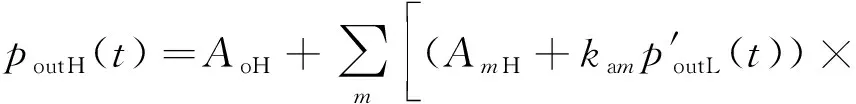
=1,2,…,6

(35)

式中：为常量；H为齿频产生压力脉动信号幅值；a为调幅系数；f为调频系数；为相位角；为齿频。

联立式(31)和式(35)可得到齿轮泵出口测点处的压力脉动傅里叶展开式：

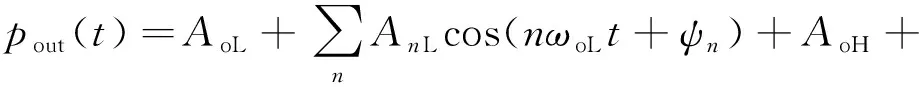
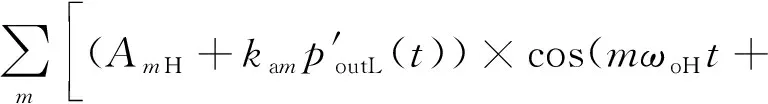
(36)

2.2 实验验证

2.2.1 实验介绍

通过比较完整的转频周期内齿轮泵出口压力脉动的仿真数据和实验数据来检验模型的正确性,齿轮泵的参数如表1所示。

表1 齿轮泵参数Table 1 Parameters of gear pump

根据国家标准(JB/T7041—2006)要求的闭式实验回路搭建液压齿轮泵出口压力脉动测试实验台。实验中分别测试了转速为2 466.6 r/min、工作负载为10 MPa,转速为1 453.2 r/min、工作负载为15 MPa,转速为773.4 r/min、工作负载为10 MPa这3种工况下齿轮泵出口测点处压力脉动信号,数据采集时的采样频率分别为10 240、10 240、5 120 Hz。分别得到不同工况下的时域图和频域图,如图7所示。从图7(a)、图7(c)、图7(e) 时域图中看到考虑了转频的脉动模型(改进模型)与实验数据的吻合度更高,而没有考虑转频的脉动模型(原来模型)与实验数据的误差较大,尤其在转速较低时更加明显,实验表明转速对压力脉动信号影响较大,随着转速提高,压力脉动信号变化趋势更加平缓,形状更加接近于标准的正弦信号。从图7(b)、图7(d)、图7(f)频域图中可以看到压力脉动的主要频率由齿轮泵的转频、轮齿啮合产生的齿频及齿频的倍频组成,转频对齿频及齿频的倍频存在明显的调制作用,证明了压力脉动信号存在不同尺度信号的线性叠加和非线性的调制,并且转频分量随着转速的提高而减小,齿频分量随转速提高而增加。因此,式(36)中由齿轮泵转频引起的基波分量傅里叶系数、和频率如表2所示。

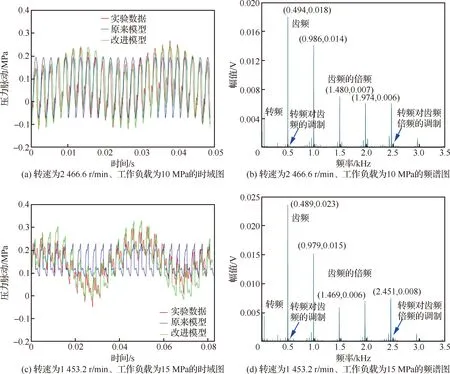
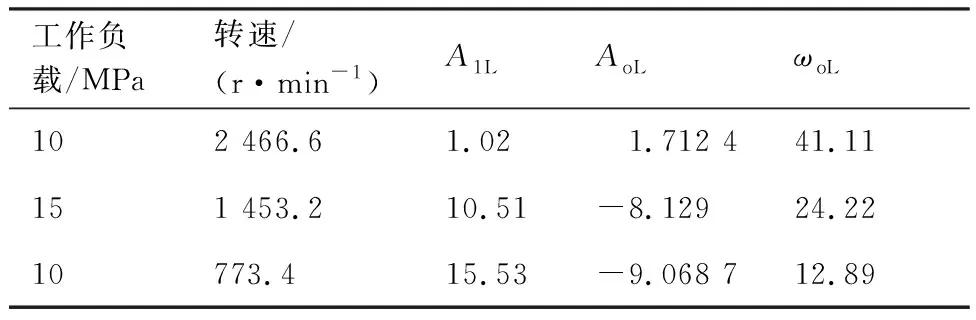
表2 不同工况下基波分量的傅里叶系数和频率

2.2.2 结果分析

从图7(a)、图7(c)、图7(e)可知改进模型仿真结果和实验数据在变化趋势上有较好的一致性,说明在研究齿轮泵压力脉动时,采用周期信号代替平稳随机信号具有一定的合理性,但也存在一些误差。误差的主要来源有：① 齿顶间隙由齿轮偏心位置和泵壳磨损两部分组成,建模中假设齿轮静止在静平衡位置,考虑转频的影响本质上是对齿轮实际中心的修正,但跟真实的回转中心还存在误差,齿顶磨损是依据经验估计的,与实际有偏差；② 端面间隙也是根据设计参数和经验估计的,与齿轮泵真实运行有偏差；③ 齿轮泵出口到高频压力传感器测量点之间并不是等直径圆管,管路有变径,造成能量损失,对压力脉动的幅值产生影响；④ 采用周期信号近似代替平稳随机信号进行处理,二者存在一定误差；⑤ 忽略了转频产生的压力脉动信号低次谐波的影响,也会产生一定的误差。

3 压力脉动的影响因素分析及工程应用展望

3.1 转速对压力脉动的影响

实验中比较了转速分别为600、800、1 000、1 500、2 000、2 500 r/min,工作负载为5 MPa这6种工况(实际转速有波动)下压力脉动的变化趋势,并定义峰值指标和脉冲指标分别如式(37)和式(38)所示。如表3所示,通过峰值指标和脉冲指标可以看出:随着转速增大,压力脉动更加平缓,即大周期压力脉动函数的幅值随着转速增大而减小,主要因为转速越高,相邻轮齿啮合的时间越短,流体流动的连续性更好,传递时相互之间的压差变化更小。

峰值指标

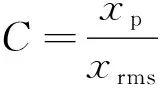
(37)

脉冲指标

(38)

表3 不同转速下压力脉动指标

3.2 工作负载对压力脉动的影响

实验中比较了工作负载分别为5、10、15 MPa,转速分别为1 500、2 000、2 500 r/min几种工况(实际转速有波动)下压力脉动的变化趋势,结果如表4所示。可见随着工作负载增大压力脉动的幅值增大,即单齿啮合压力脉动幅值和大周期压力脉动的幅值随着工作负载增大而增大,并且工作负载对压力脉动的影响要大于速度对压力脉动的影响。主要因为工作负载越高,流体元受到的剪切力越大,由于流体的易变性,流体质点的相对运动增大,流体流动的连续性减弱,传递时相互之间的压差变化增大。

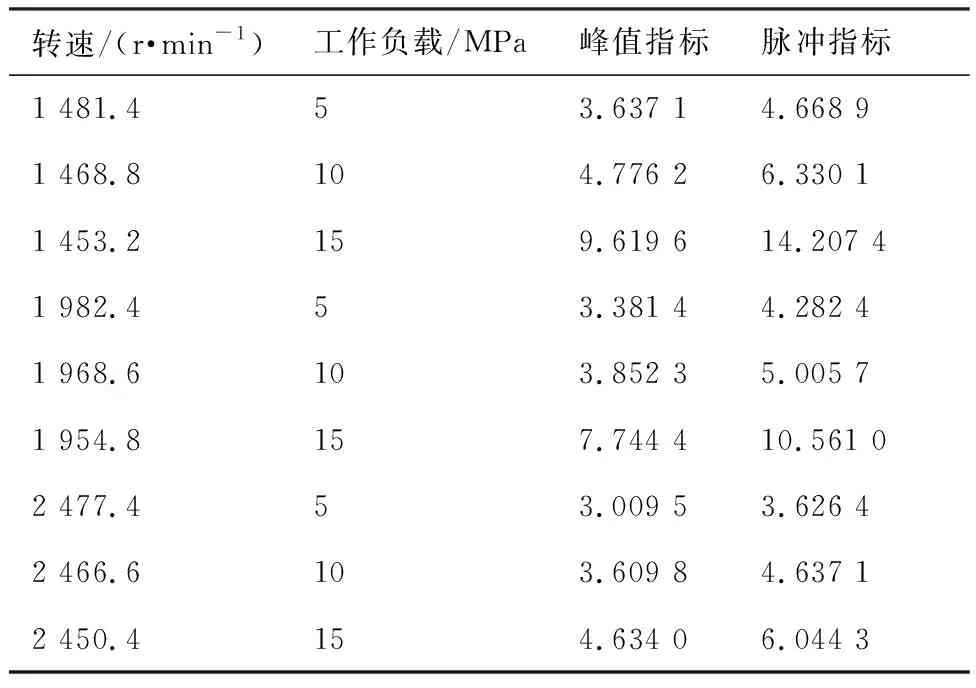
表4 不同工作负载下压力脉动指标Table 4 Pressure pulsation index at different workloads

3.3 工程应用展望

在外啮合齿轮泵的实际使用过程中,齿轮泵出现致命失效、完全失效等失效形式的几率较小,最常见的失效形式为退化失效,具体表现为输出流量或压力不足。造成这种失效形式的主要原因是齿轮泵在运行过程中内部摩擦副不停接触磨损导致的。磨损失效主要有3种形式,分别为端面磨损、齿面磨损和齿顶磨损,其中端面磨损导致的泄漏占总泄漏量的80%左右,是影响泄漏的最主要因素。行业标准规定实际使用中容积效率低于85%为失效,但是流量的测量存在测量误差大、准确率低、信号变化不明显等问题。因此,研究压力脉动信号与齿轮泵故障之间的内在关系具有重要的意义。

齿轮泵中流量的传递如图8所示,假设在端面磨损前后输入的流量恒定,且不考虑外泄漏,则输出流量分成两部分：一部分由泵的出口管路输出用于执行机构做功,即,另一部分由泵的内泄漏做无用功,即Δ。泄漏量与间隙之间的关系为

(39)

式中：Δ为间隙两端压差；为液压油动力黏度；为间隙长度；为间隙宽度。

齿轮泵出口管路为圆管,则输出流量与流速之间的关系为

=·

(40)

式中：为平均流速；为管路截面积。

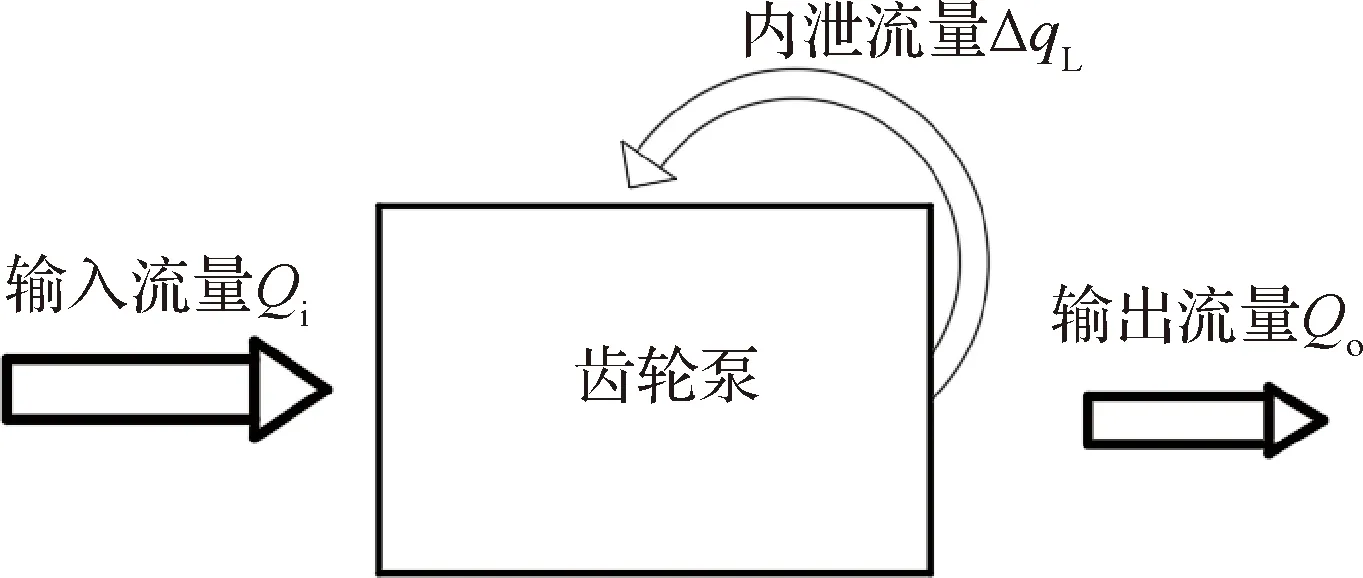
图8 齿轮泵的流量输运Fig.8 Flow transport of gear pump

由式(39)可知,间隙增大,齿轮泵泄漏量增大,则齿轮泵出口流量减小。磨损前后齿轮泵出口管路直径大小不变,由式(40)可知平均流速减小。平均流速与脉动速度′之间的关系为

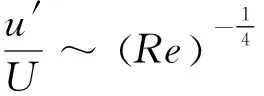
(41)

式中：为雷诺数。

由式(41)可知,主流速度减小,则脉动速度′也相应减小,脉动的速度场发生变化,式(24) 表明,一点的脉动压力是该点领域中脉动速度场的泛函,脉动速度场的变化会导致脉动压力的变化。因此,压力脉动信号作为齿轮泵磨损故障的特征信号具有一定的合理性。

齿轮泵通过出口控制体体积变化实现流体的排出,因此出口压力脉动是齿轮泵的固有特性。从优化齿轮泵压力脉动减少故障的角度分析,提出以下几点工程建议：① 在设计齿轮泵时要将固有频率和压力脉动频率错开,以免发生共振；② 合理设计齿轮泵浮动轴套背面的密封圈形状及安装位置,尽量减少浮动轴套的偏斜,保证合理的端面间隙；③ 改变主、从动齿轮的齿数、外形尺寸来减少出口流量脉动,从而达到减少压力脉动的目的。