一道省质检题的溯源与变式

福建省上杭县第一中学 (364200) 伍养群福建省上杭县明强中学 (364200) 张 磊

本文为福建省上杭县教师进修学校2021年度课题“变式教学在高中数学课堂教学中的运用策略研究”(GZ20211001)的阶段性成果.

数学试题的精彩是由其内在联系引起，在教学中善于对试题的本质规律进行分析和追溯，并作深入的思考与变式.真正实现会一道题，达到懂一类题是每位数学教师在课堂教学中必须探究和提升的课题.

(1)建立适当的坐标系，求C的方程；(2)A,B是C上不同的两点，且直线AB与以OA为直径的圆的一个交点在圆O上．求证：以AB为直径的圆过定点．

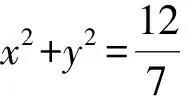
分析2：由于上述命题的推理可逆，所以交换上题中的条件与结论可以得到其命题的正确性.

分析7：根据点A与B的特殊位置生成的数量关系，并结合椭圆中的变量a,b,c满足的条件推断出一般性的命题.

分析8：保留垂直的位置关系，但改变点O的位置，让点O在直线(x轴)上运动，探求直线AB是过定点还是与定圆相切？

分析9：若改变点M的位置，让点M在椭圆上运动，探求直线l是否还过定点？

思考2：利用弦l经过定点这结论和已知定点M可进行再创造：以两定点组成线段(定值)为直径作圆交直线l于点D，为了隐藏弦l经过定点，则设置过点M作MD⊥l，再提出问题：是否存在定点T，使得|DT|为定值即为2020年山东省高考数学试卷(新高考全国Ⅰ卷)第22题，若改变MA,MB的斜率满足的条件，也可作相应的结论.

分析10：若改变MA,MB的斜率满足的条件，并用抛物线代替椭圆作探究.

变式6 (自编)已知动圆C与定圆F：x2+y2-2x=0相外切，且与直线l:x=-1相切．

(1)求动圆圆心C的轨迹方程Γ；(2)若M(1,2)，点A，B在曲线Γ上，且KMA+KMB=-1，MN⊥AB，N为垂足．证明：存在定点T，使得|TN|为定值．

分析11：保留点O的位置，但改变垂直的位置关系，探求直线l与椭圆的两个交点和原点组成的三角形的面积是否为定值？

总之，对数学试题的教学与研究，决不能只浮在表面，务必要透过现象看本质，并深入思考和拓展其内在的规律，才能让试题的光彩达到淋漓尽致的高度，努力构建高效的课堂教学.