一个经典结论的初等证明

湖北省武汉市教育科学研究院 (430032) 孔 峰湖北省武汉市黄陂区第一中学盘龙校区 (430312) 李红春

解析几何中有一些美妙的结论，背景深刻，结论简洁，极具应用价值，深受教师喜爱，不少考题在命制时，也只是这些结论的具体化.笔者在一线教学中发现，有些结论知道的人不少，却鲜有人能给出严谨的证明，让人觉得美中不足.本文给出一个结论的初等证明，以飨读者.

结论过曲线Γ：Ax2+Bxy+Cy2+Dx+Ey+F=0上一点P(x0,y0)作两条直线PM、PN分别交曲线Γ于M、N两点，连接MN，若满足下列条件中的一个，则直线MN要么方向一定，要么恒过定点.

(1)若kPM·kPN=λ(λ≠0);

(2)若kPM+kPN=μ.

(1)若kPM·kPN=λ(λ≠0)，则

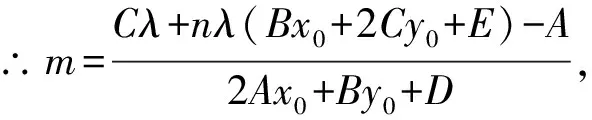
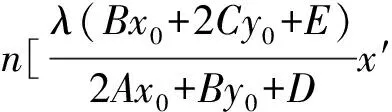
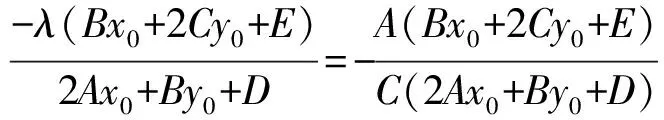
(2)若kPM+kPN=μ时，即kPM+kPN=

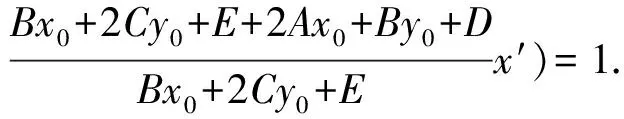
若Cμ+B=0时，直线MN的斜率

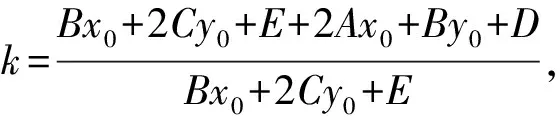
本文通过对这一经典数学结论的证明，让读者知其然，更知其所以然，不但体现了数学思维的严谨性，更为今后命制这类试题的科学性提供了支撑.