依托数学文化 玩转平面向量
2022-10-10湖北省襄阳市第四中学441021娜湖北省襄阳市第一中学441000
湖北省襄阳市第四中学 (441021) 范 娜湖北省襄阳市第一中学 (441000) 王 勇
数学文化是贯穿整个高中数学的重要内容,在高考中,以数学文化为命题背景的试题立意深远、构思精巧、内涵丰富,既能考查数学知识、能力、思想和方法,又能加深对中外数学文明的了解,增强爱国主义情怀,提高数学文化素养,丰厚数学文化底蕴.融入对数学文化的考查已成为新一轮高考命题改革的一个显著特征.下面精选以数学文化为依托的平面向量问题七例并分类解析,旨在探索题型规律,揭示解题方法.
一、以“八卦模型图”为依托
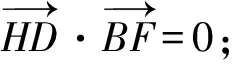

图1 图2
A.4 B.3 C.2 D.1
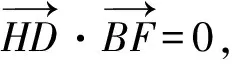
点评:本题中八卦模型图只是为了引出八边形ABCDEFGH的一个载体,重要的是理解平面图形,即正八边形ABCDEFGH所包含的几何性质,在正八边形ABCDEFGH中,通过对几何图形性质的理解,利用向量的和差运算、数量积运算等,逐一验证给出的四个结论是否正确而得解.
二、以“赵爽弦图”为依托
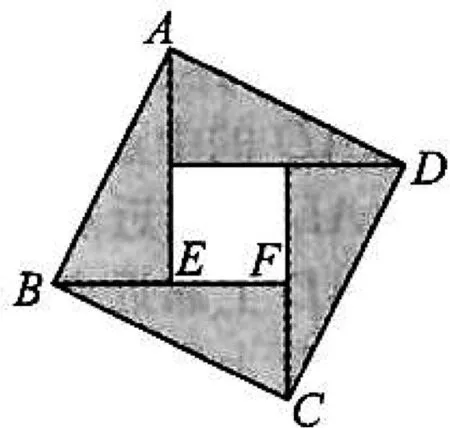
图3

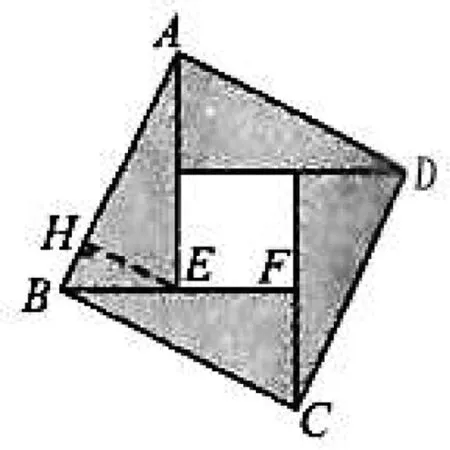
图4
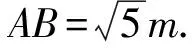
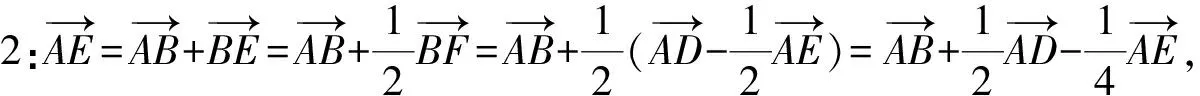
点评:本题借用“赵爽弦图”考查平面向量的线性运算,具体推理时有一定的难度.

图5
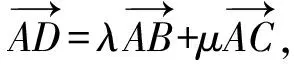

图6

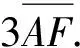
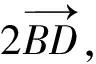
点评:本题以“赵爽弦图”的类比图为背景命制,新颖别致,韵味十足.主要考查平面向量的线性运算,具体推理时,需添加辅助线,极富思考性和挑战性,是一道难得的好题.
三、以“黄金分割”为依托
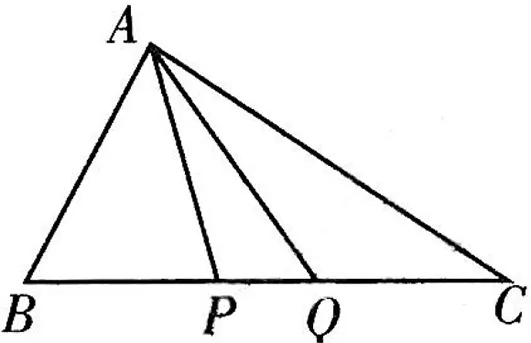
图7
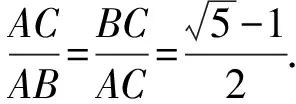

点评:本题以黄金分割数及黄金分割点为载体命制,主要考查平面向量的线性运算,对运算求解能力要求较高.
四、以“勾股定理”为依托

图8

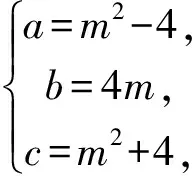
点评:本题首先通过已知确定三角形的三边长,然后利用平面向量数量积运算求解即可.
五、以“欧拉线”为依托
例6 (2021·深圳市调考题)著名数学家欧拉提出了如下定理:三角形的外心、重心、垂心位于同一直线上,且重心到外心的距离是重心到垂心的距离的一半.此直线被称为三角形的欧拉线,该定理则被称为欧拉线定理.设点O,H分别是△ABC的外心、垂心,且M为BC的中点,则( ).
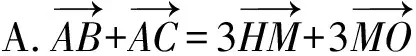
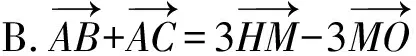



图9
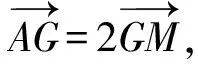
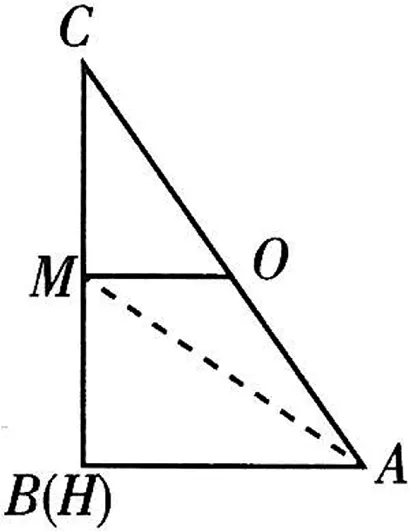
图10
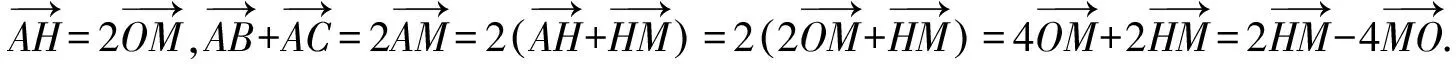
点评:本题以三角形的欧拉线及欧拉线定理为背景命制,主要考查平面向量的线性运算,具体推理时,有一定的难度.解法2利用特殊图形法可轻松获解,敬请同学们仔细品味和充分借鉴.
六、以“六芒星”为依托

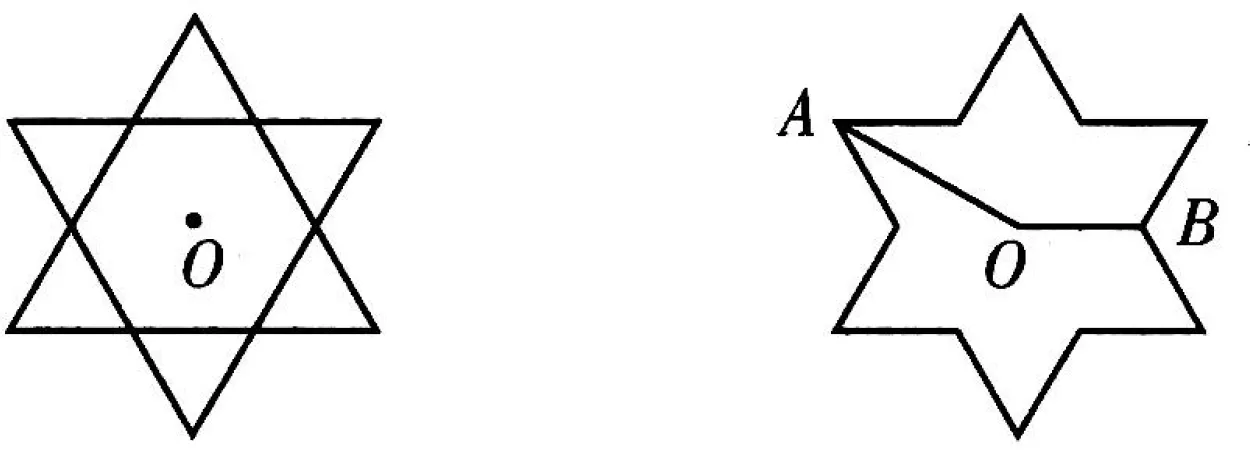
图11 图12
A.-6 B.1 C.5 D.9


图13
点评:本题是以“六芒星”为背景命制的多选题,图形美观大气,主要考查平面向量的线性运算,分类讨论思想考查充分,借助图形的结构特征求出的取值范围,进而求出的可能取值.
纵观以上各例,我们发现,此类平面向量题一般是从中外优秀传统文化中挖掘素材,将数学文化与平面向量知识有机结合,要求考生对试题所提供的数学文化信息材料进行整理和分析,在试题营造的数学文化氛围中,考查平面向量的基础知识、基本技能、基本思想、基本活动经验,感受数学的思维方式,体验数学的理性精神.
