例析函数对称性质及其应用
2022-10-10福建省厦门实验中学361100沈振军
福建省厦门实验中学 (361100) 沈振军
在近年高考数学试题中,以抽象函数或具体函数为载体考查函数的对称性题型是常考和创新题型,此类题型突出对转化与化归思想、数形结合思想的考查与应用;要求学生具备独立分析问题,解决问题的重要能力;同时体现了对数学抽象,逻辑推理等数学核心素养考查.本文从关于轴对称的函数、关于点成中心对称的函数、关于直线y=x对称的两个函数、函数与导函数的对称性关系、利用函数的对称性找不等关系等五个方面的性质例析其应用.
1.关于轴对称的函数
性质1 函数y=f(x)关于直线x=a轴对称等价于f(a+x)=f(a-x)(或f(2a-x)=f(x)).
例1 若函数f(x)=2|x-a|(a∈R)满足f(1+x)=f(1-x),且f(x)在区间[m,+∞)上单调递增,则m的最小值等于.
解析:由函数f(x)满足f(1+x)=f(1-x),可得其关于x=1对称,故a=1,则f(x)=2|x-1|,利用复合函数单调性的判断方法,可知函数f(x)在区间[1,+∞)递增,所以m的最小值为1.

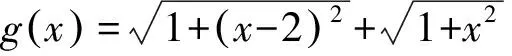
性质2 若函数y=f(x)同时关于直线x=a与x=b轴对称,则函数f(x)是周期函数,且周期T=2|a-b|.
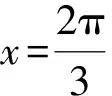
A.f(2) C.f(-2) 性质3 若函数y=f(x)关于直线x=a轴对称,且在x=a处可导,则f′(a)=0. 性质4 函数y=f(x)关于点(a,b)中心对称等价于f(a-x)+f(a+x)=2b(或f(2a-x)+f(x)=2b). 性质5 (1)若函数y=f(x)同时关于点(a,0)和点(b,0)中心对称,则函数f(x)是一个周期函数,且周期T=2|a-b|;(2)若函数y=f(x)既关于直线x=b对称,又关于点(a,0)成中心对称,则函数f(x)是一个周期函数,且周期T=4|a-b|. 例7 若函数f(x)的定义域为R,且f(x+1)与f(x-1)都是奇函数,则( ). A.f(x)是偶函数 B.f(x)是奇函数 C.f(x)=f(x+2) D.f(x+3)是奇函数 解析:f(x+1)与f(x-1)都是奇函数,则函数f(x)关于(1,0)和(-1,0)中心对称,则函数f(x)是周期函数,且周期T=4,则f(x+3)=f(x+3-4)=f(x-1),则f(x+3)是奇函数,故选D. 性质6 若两个函数f(x)和g(x)互为反函数,则这两个函数的图像关于直线y=x对称. 性质7y=f(x)是可导函数,若y=f(x)的图像关于点(m,n)对称,则y=f′(x)图像关于直线x=m对称;若y=f(x)图像关于直线x=m对称,则y=f′(x)图像关于点(m,0)对称. 性质8 (1)已知函数f(x)关于点(m,n)成中心对称,且f(x)为增函数.若x1+x2>2m,则有f(x1)+f(x2)>2n.若x1+x2<2m,则有f(x1)+f(x2)<2n,反之亦然;(2)已知函数f(x)关于点(m,n)成中心对称,且f(x)为减函数.若x1+x2>2m,则有f(x1)+f(x2)<2n.若x1+x2<2m,则有f(x1)+f(x2)>2n,反之亦然. 例13 定义在R上的连续函数f(x)满足f(-x)=-f(x+4),当x>2时,f(x)单调递增,若x1+x2>4且(x1-2)(x2-2)<0,则f(x1)+f(x2)和0的大小关系为. 解法一(代数方法):由x1+x2>4且(x1-2)(x2-2)<0,则可假设x1<2,可得x2>4-x1>2,利用函数f(x)在x>2单调递增,可得f(x2)>f(4-x1),利用f(-x)=-f(x+4),可得f(4-x1)=-f(x1),则可得f(x1)+f(x2)>0. 解法二(对称函数的方法):由f(x)满足f(-x)=-f(x+4),可知函数f(x)关于点(2,0)成中心对称,连续函数f(x)在x>2单调递增,可得f(x)在整个定义域上单调递增,由x1+x2>4,则可得f(x1)+f(x2)>0. 综上实例可以看出,函数的对称性与函数的奇偶性、单调性、最值、周期性、方程的根及图像的交点等性质结合,即考查从特殊(奇偶性)到一般(轴对称和点对称)的推理能力,又考查了化归转化能力.此类题灵活性强,条件较隐蔽,能较较好地考查学生数学核心素养的要求.



2.关于点中心对称的函数





3.关于直线y=x对称的两个函数



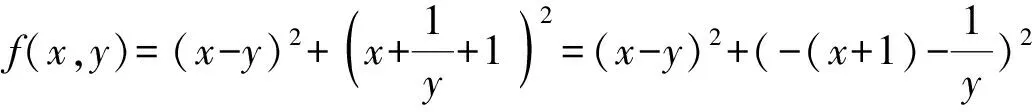
4.函数与导函数的对称关系




5.利用函数的对称性找不等关系
