例析阿波罗尼斯圆的命题策略

四川外国语大学附属外国语学校 (400000) 郭海峰重庆市重庆实验外国语学校 (400039) 李小燕

在近几年的高考题、模拟题中，阿波罗尼斯圆(以下简称阿氏圆)越来越受到出题老师的青睐.笔者在梳理相关材料时，总结了该圆的几种考察方式，现整理成文，以飨读者.

一、阿氏圆的定义[1]

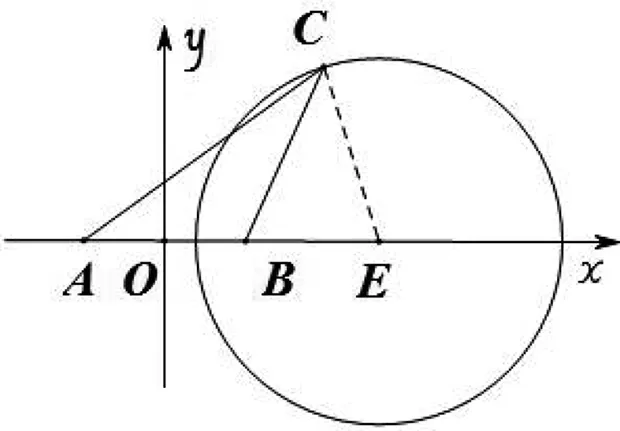
图1

二、阿氏圆与其他圆锥曲线的结合

在阿氏圆的定义中，涉及到两个定点与定比例.在常见的圆锥曲线中，也涉及到较多的定点与定值，这就与两者的结合提供了理论基础.

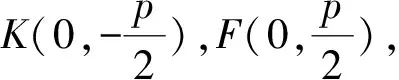
三、阿氏圆的逆向考察

在阿氏圆的定义中，涉及到两个定点，定值以及最终的轨迹圆.能否根据圆以及定值来考察两个定点之间的关系呢？或者考察定值的范围问题呢？

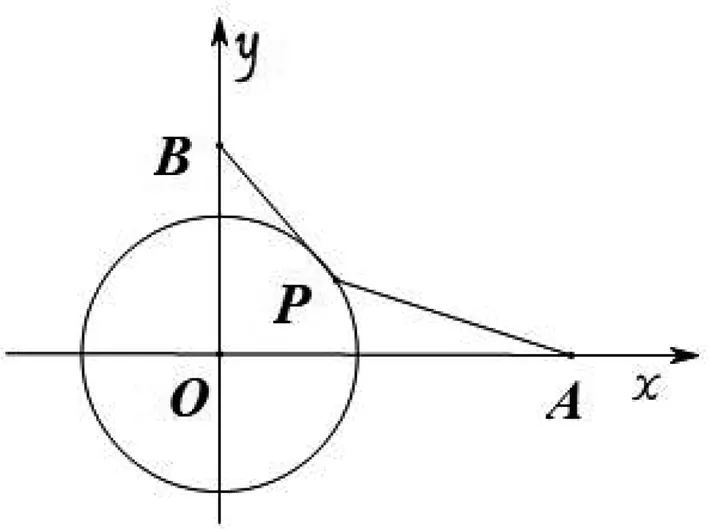
图2

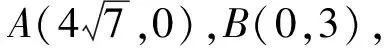
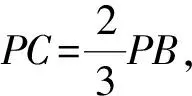
例4 (自编)已知点A(1,0)，B(2,0)以及圆O:x2+y2=1，设点P为圆O上的动点，若|PB|=λ|PA|，求λ的取值范围.

注意到在阿氏圆的定义中，两个定点与阿氏圆的圆心在同一直线上，根据圆的对称性在给定的阿氏圆中，存在无数对定点符合相关的比例.具体如下：

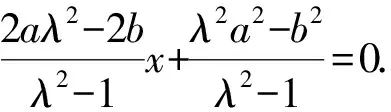
设过点Q作出的射线与两个同心圆的交点为A1，B1，结合圆的对称性可知|PB1|=λ|PA1|成立，即可知满足该比例关系的定点有无数对.

四、阿氏圆在立体图形中的应用

图3