由一道解几题谈学生运算能力的培养

安徽省淮北市第一中学 (235000) 王 旭

数学运算素养作为数学学科六大核心素养之一，是数学能力中的基本能力，学生通过运算可以促进数学思维发展，形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学精神[1].其中圆锥曲线一直是高考数学的重难点，是考察学生数学运算素养、逻辑推理以及直观想象的重要载体，在此基础上，对学生的运算能力有较高的要求.

针对学生的答题情况，本文以2021年全国乙卷的第21题为例，对其进行深度解析与适当延展，就高中生的数学运算能力的培养进行思考.

1 真题再现

已知抛物线C:x2=2py(p>0)的焦点为F，且F与圆M:x2+(y+4)2=1上点的距离的最小值为4．

(1)求p；(2)若点P在M上，PA、PB是C的两条切线，A,B是切点，求△PAB面积的最大值．

2 试题分析

本题涉及到抛物线和圆两种二次曲线，第(1)问比较简单，只需要对已知条件进行代数转化即可求解.第(2)问涉及到P、A、B三个动点，分析可知当点P确定时，切点A、B也就随之确定，所以△PAB面积的变化是由点P主导的.第(2)问的解答主要存在以下几种问题：

问题一：求解三角形面积的最值问题，在选择面积公式后不知道如何确定主元；问题二：设切线PA、PB的直线方程，利用传统的三角形面积公式求解，但在求解过程中不会处理切点弦AB所在的直线方程；问题三：用k1,k2分别表示切线PA、PB的斜率，但不会处理这两个参数的关系.

3 解法剖析

易得第(1)问中p=2.下面重点讨论第(2)问.

思路一：设点求直线，利用导数求切线.

思路二：巧用切点弦直线方程，优化运算过程.

思路三：以方程作为切入点，利用函数思想简化计算.

思路四：以切点作为切入点，利用参数方程简化计算.

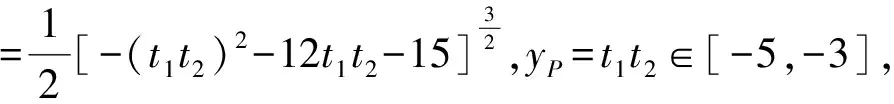
4 教学启示

4.1 逐本溯源，把握问题本质

一题多解可以有效地帮助学生探究题目中蕴含的本质，建构知识之间的联系，寻找通式通法，探究问题本质，也可以帮助学生连接知识网络.这道题考察的是抛物线中阿基米德三角形的面积问题，阿基米德三角形的相关性质和结论也备受高考试题和模拟题的青睐，在近几年的考试中屡次出现.

比较上述两题，也是涉及到阿基米德三角形的面积问题，由此我们可以归纳出阿基米德三角形面积的一般解法，从切线方程入手，得到两条切线的交点坐标，再利用弦长公式求得切点弦长，继而得到面积的表达式，如以变式1为例其解为：

4.2 优化运算，发展核心素养

在《中国高考评价体系》中提出“高考‘立德树人、服务选才、引导教学’的核心功能”[2]，高考客观上对于高中教学具有很重要的引导作用，对高考题目的研究可以判断相关知识点的考法以及对来年高考命题的把握，因此研究高考题目对高三的复习备考至关重要.在高三备考中，教师应教会学生如何将题目中的条件“翻译”为几何语言以及代数语言，学会用数学的语言进行表达解题的策略和方法.解析几何是将几何问题代数化，用数表形，用形转化数，在例题讲解中可以引导学生在运算时边观察边转化，减少不必要的运算.

提高学生的数学运算能力不仅仅是单纯的计算技能的培养，更是培养学生数学思维的必要条件.因此教学中应树立正确的数学运算观.同时要养成学生良好的运算习惯.并且教学中特别强调学生应坚持练习，不轻言放弃.波利亚在《怎样解题》一书中提到：“教学生解题是意志的教育”，面对较为复杂的运算时学生坚持不懈地进行处理，获得的不仅仅是克服困难后收获的喜悦，更是在培养自身不言放弃的品质.