花岗岩Kong-Fang 流体弹塑性损伤材料模型参数研究*

2022-10-10聂铮玥丁育青宋江杰林玉亮

爆炸与冲击 2022年9期

聂铮玥，丁育青，宋江杰，彭永，林玉亮，陈荣

（1. 国防科技大学理学院, 湖南长沙 410073；2. 中国人民解放军96901 部队, 北京 100094）

预测岩石类材料在动态条件下的力学响应及破坏行为一直是数值计算中的重难点，建立合适的动态力学模型并选取适当的材料模型参数十分重要。目前常用的岩石类材料动态模型包括：Holmquist-Johnson-Cook 模型（HJC 模型）、Karagozian-and-Case 模型（K&C 模型）、Riedel-Hiermaier-Thoma 模型（RHT 模型）、Johnson-Holmquist 模型（JH-2 模型）、Talyor-Chen-Kuszmaul 模型（TCK 模型）等，并被应用于如冲击、爆炸、侵彻等多种动态过程的仿真分析中。研究表明，这些模型在运用时并不都能得到较理想的效果，原因在于模型本身存在一定的不足，无法很好地反映岩石材料的某些特征。一些学者对现有模型进行了部分修正，并将改进后的模型应用于相关的动态分析中，获得了较好的结果。但建立更为合理的、完善的岩石类材料动态力学模型仍然十分必要。

Kong 等基于塑性损伤理论建立了一种新的混凝土动态力学模型（Kong-Fang 流体弹塑性损伤材料模型，KF 模型），该模型定义了基于3 个应力不变量的屈服面，并对压缩和拉伸损伤计算进行了区分。模型中引入了部分关联流动法则，可以较好地描述混凝土材料的剪胀行为。通过多种单元数值试验以及爆炸、冲击等动力学实例的模拟分析，对比HJC、K&C 及RHT 模型的模拟结果，验证了KF 模型的适用性。Huang 等进一步对KF 模型进行了修正以适用于岩石材料，他们利用大量硬岩实验数据标定了模型中的部分参数，同时采用简明的半经验公式来描述动态增长因子随应变率的变化规律。通过多单元拉压数值试验及岩石劈裂、冲击实例的仿真计算，验证了修正模型对岩石的动态响应具有较好的预测能力。

考虑到天然岩石的力学性质差异较大，本文中将以山东五莲地区的花岗岩对研究对象，采用KF 模型，根据模型参数定义，一方面，通过准静态单轴压缩、劈裂、常规三轴及动态分离式霍普金森杆压缩实验对模型中的强度参数进行确定，同时利用动态巴西圆盘实验结果验证应变率相关参数的有效性。另一方面，通过平板撞击实验拟合模型中的状态方程参数；最后结合实测参数值，利用KF 模型对花岗岩侵彻试验过程进行仿真，通过对比计算得到的靶体侵彻深度和弹坑尺寸与实际试验的结果，验证材料模型及参数值的适用性。

1 KF 模型简介及参数分类

1.1 KF 模型简介

KF 模型是一种可以描述岩石类材料在高压和高应变率条件下动态响应的计算本构模型。模型主要对屈服面、应变率效应和损伤累积进行了定义，此外，还采用了部分关联流动法则和多项式状态方程来分别描述岩石在低压压缩下的剪胀性和高压压缩下的变形特征。

1.1.1 基于三个应力不变量的屈服面

KF 模型采用了压缩子午线的最大强度面σ和残余强度面σ，其表达式分别为：

式中：和分别为无侧限单轴压缩强度和拉伸强度；为静水压力；为总损伤；、为与强度面相关的材料常数；ψ 为拉压子午线的比值，表示与压力相关的函数。最初，KF 模型中定义ψ 为的分段函数，具体根据混凝土的三轴压缩和拉伸实验数据确定，后来Huang 等考虑到硬岩的压缩性质与混凝土存在差异，对ψ 进行了校准以适用于硬岩。

当材料并未达到最大强度面σ或残余强度面σ时，当前破坏面则依据当前岩石损伤情况对σ和σ进行插值确定：

式中：为偏应力第二不变量；′为当前子午线与压缩子午线的比值，其值可通过ψ()与Lode 角计算获得，函数形式与RHT 模型中的参数(θ)（θ 为Lode 角）计算公式一致。

1.1.2 拉压分离的应变率效应

岩石材料动态强度具有明显的率效应，因此KF 模型将当前破坏面进一步改进为：

式中：η 为动态增长因子，其值为岩石动态强度与准静态强度的比值。

考虑到拉压条件下岩石将表现出不同的应变率效应，KF 模型中分别定义了压缩强度动态增长因子η与拉伸强度动态增长因子η，由于原始计算公式较复杂，文献[17]中采用一种半经验的简洁公式对其进行了改进：

式中：α、β、θ 为材料参数， ε˙ 为应变率。

1.1.3 状态方程

当压力较高时，岩石材料的强度和结构的影响一般可以忽略，此时仅需考虑材料的体积变形，因此模型采用了单独的多项式状态方程来表征岩石在高压条件下的体积压缩行为：

式中：、和为状态方程材料参数，为体应变。

此外，模型中定义了材料损伤、变形及单元删除。（1）考虑到岩石材料在拉压荷载下的破坏机理不同，分别定义了拉伸损伤和压缩损伤，并根据和计算了岩石材料的总损伤。在计算损伤时共定义了6 个损伤累积相关参数，对于硬岩，文献[17]中给出了这类参数的建议值：=0.04、=2.3、γ=1、=3、=6.93、ε=0.001 5，因此，在本研究中也将这类参数作为常数处理。（2）为了表征岩石在低围压压缩荷载下的剪胀性，基于K&C 模型中的塑性势函数，引入了部分关联的塑性流动法则，得到了相应的破坏面与应力更新计算公式。（3）模型中还采纳了两种单元删除准则，分别是基于损伤的拉伸删除准则和基于等效塑性应变的压缩删除准则，以表征岩石在遭受如爆炸等动载荷时材料前端和后端出现的成坑和剥落等破坏特征。由于损伤累积部分的参数为定值，而部分关联塑性流动法则与单元删除准则中没有涉及新的参数，因此本文中不再介绍。

1.2 模型参数分类及确定方法

为了获得待研究花岗岩材料的KF 模型参数值，需确定各参数的实验方法。首先，根据模型定义可将待确定参数分为材料基本强度参数、强度相关参数和状态方程相关参数，见表1。材料基本强度参数、和ν 的确定可通过无侧限单轴压缩实验进行；对于参数的确定，由于直接拉伸实验费用高、成功率较低，而巴西劈裂实验制样方便、操作简单、成功率高，因此将采用劈裂实验获得的材料劈裂抗拉强度来代替参数；强度面相关的材料常数、的确定则需要大量三轴压缩实验数据；由式（5）～（6）可知，应变率相关的参数α、β、θ 可通过SHPB 实验确定，同时可利用SHPB-BD 实验结果对拟合参数值的有效性进行验证；对状态方程相关参数的确定，可先通过平板撞击实验获得岩石的冲击雨果纽数据，然后拟合材料的压力-体应变关系曲线（-曲线）获得。

表1 KF 模型参数的分类及实验确定方法Table 1 Parameter classification and experimental determination method of KF model

2 准静态实验及相关参数确定

2.1 实验样品

选用产自山东五莲地区的粗中粒角闪二长花岗岩，岩石为二长半自形粒状结构，块状构造，主要矿物为斜长石(Pl)、钾长石(Kfs)、石英(Qtz)，共占矿物总量的90%。次要矿物为角闪石(Hbl)、黑云母(Bt)、辉石(Px)；蚀变及充填矿物为绢云母、绿帘石。岩石的实物照片和显微图像如图1 所示。

图1 岩石试件的实物照片和显微图像Fig. 1 Photographs and micrographs of rock samples

根据相关的实验规范及实验机对试件的要求，制作各准静态实验的岩石试样：无侧限单轴压缩及常规三轴实验的试件为直径50 mm、高100 mm 的标准圆柱形；劈裂实验试件为直径50 mm、高25 mm 的圆盘。为了保证实验结果的可靠性，每种实验均开展了重复实验。

2.2 准静态单轴压缩及劈裂实验

分别利用TAW2000 岩石三轴伺服压缩机及WDW-500E 微机控制电子式万能试验机对花岗岩试件进行准静态单轴压缩和劈裂实验，如图2 所示。实验中均采用变形控制加载，设置变形速率分别为0.06、0.03 mm/min，使得实验过程中试件的应变率为10s。

图2 花岗岩单轴压缩及劈裂实验Fig. 2 Typical view of uniaxial compression test (UCT) and splitting test (ST)

对单轴压缩实验获得的轴向压缩应力-应变曲线进行求导，其中弹性段导数即为试件的弹性模量，同时采用/2 处的环向应变和轴向应变来计算各试件的泊松比υ。结合各试件的单轴抗压强度值及劈裂拉伸强度，利用两倍标准差法剔除异常值，并计算剩余有效数据的平均值作为花岗岩试件的KF 模型参数值，结果见表2。

表2 花岗岩的基本强度参数值Table 2 Basic strength parameters of granite

2.3 准静态常规三轴实验

利用MTS815 型电液伺服岩石力学试验机对花岗岩试件进行准静态常规三轴实验，为了满足参数确定需求，设置了5 种不同的围压水平：10、20、30、40、50 MPa。其中10、20 MPa 工况各进行1 次实验，30、40、50 MPa 工况重复3 次实验。如图3 所示，将试件置于实验平台上，先施加一定的轴向压力防止试件滑动，然后再以1～3 MPa/min 的加载速度施加围压至设定值。保持围压约5～10 min，确定不漏油后，以0.06 mm/min 的加载速度施加轴压，直至试件破坏。

图3 常规三轴实验Fig. 3 A view of triaxial compression test (TXC, σ2=σ3)

花岗岩试件的常规三轴压缩应力-应变曲线如图4 所示。由图4 可知，围压实验的重复性较好，岩石的峰值强度随围压的增加而增加。由式（1）可知，确定参数、只需利用强度面应力值。因此，利用各试件的围压及相应的轴向峰值强度分别计算出各工况下的偏压力（σ=σ-σ）和静水压力（=1/(3(σ+2σ))），结果见表3。进一步对、进行拟合，获得如图5 所示的参数拟合值：=0.36，=0.09/。

图4 常规三轴实验花岗岩试件应力-应变曲线Fig. 4 Stress-strain curves of rock samples in TXC tests

表3 不同围压条件下试件的轴向峰值强度、偏压力与静水压力Table 3 The strength, deviatoric pressure and hydrostatic pressure of rock samples under different confining pressures

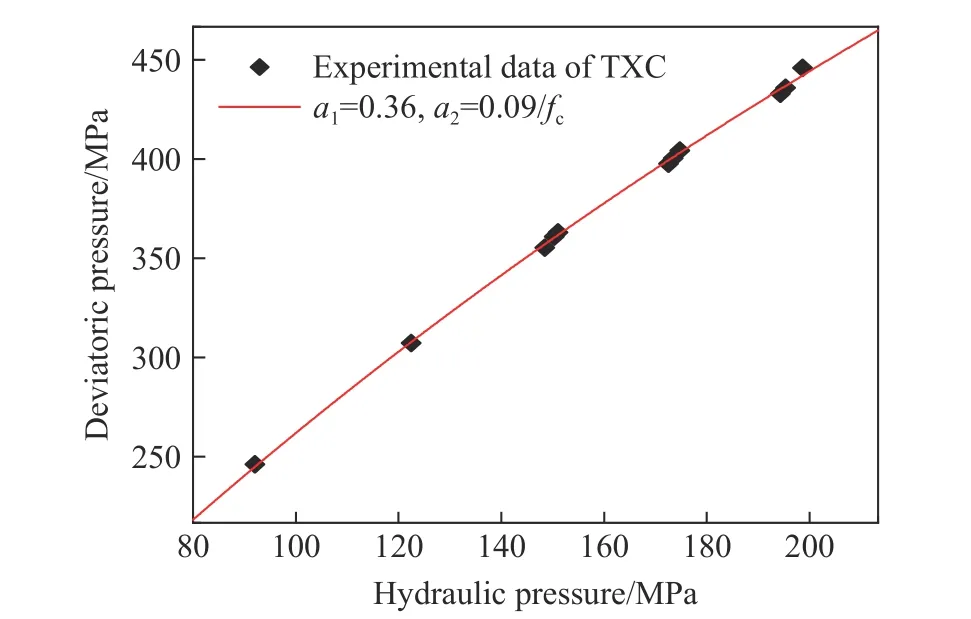
图5 花岗岩a1、a2 参数拟合结果Fig. 5 Fitting results of parameters a1 and a2 of granite

3 动态实验及相关参数确定

3.1 SHPB 及SHPB-BD 实验

根据相关的实验标准，基于50 mm 杆径的分离式霍普金森杆实验系统开展SHPB 及SHPBBD 实验。入射杆、透射杆分别长3.0、1.8 m，材料均为马氏体钢，两种实验采用的试件均为 ∅ 38 mm×19 mm的圆盘形试样。经过力平衡校验后，计算各有效实验的试件应变率 ε˙ 、应变ε 及应力σ：

式中：为实验杆的一维弹性波速，ε、ε、ε分别为入射应变、反射应变和透射应变，为试样长度，σ为SHPB 实验中试样的压缩应力，σ为SHPB-BD 实验中试样的拉伸应力，为杆的弹性模量，为杆的横截面积，为试样的横截面积，为试样直径，为试样厚度。

为了确定并检验KF 模型中的应变率相关参数α、β、θ，分别进行了14 次动态压缩实验（剔除误差较大的一组数据）和15 次动态劈裂实验，试件平均应变率为83～360 s（动态压缩）和133～245 s（动态劈裂）。实验所得的应力-应变曲线如图6 所示，从图中可以发现，花岗岩具有一定的应变率效应。提取各实验中平均应变率及峰值强度并计算相应的η值与η值，结果见表4。利用表4 中数据，结合式（5）～（6）对α、β、θ 进行拟合及验证。图7 中展示了拟合得到的参数值：α=0.06、β=3.47、θ=1.83。图8 为利用SHPB-BD 实验数据对参数进行验证的结果，由图8 可知，拟合得到的参数值有较好的适用性。

图6 花岗岩SHPB、SHPB-BD 实验应力-应变曲线Fig. 6 Stress-strain curves of SHPB and SHPB-BD tests of granite samples

图7 基于SHPB 实验数据拟合得到的α、β、θ 参数值Fig. 7 Parameter values of α, β and θ fitted by SHPB tests data

图8 利用SHPB-BD 实验数据对α、β、θ 值进行验证的结果Fig. 8 Validation of α, β and θ values by SHPB-BD tests data

表4 SHPB、SHPB-BD 实验的平均应变率及相应的 ηc 、 ηt 值Table 4 Average strain rates and corresponding ηc and ηt values obtained from SHPB and SHPB-BD experiments

3.2 平板撞击实验

为了获得更干净稳定的信号，基于57 mm 口径一级轻气炮，采用反向撞击法开展实验。考虑到获取信号不能受到追赶稀疏波及边侧稀疏波的影响，飞片与靶板尺寸均设计为 ∅ 50 mm×10 mm，其中靶体材料为无氧铜。具体的实验原理为：当岩石飞片撞击无氧铜靶时，利用电探针测得飞片的速度，利用DISAR（displacement interferometer system for any reflector）系统测得靶板背面的自由面质点速度。根据应力波原理，结合冲击绝热线方程及Rankine-Hugoniot 方程可知，岩石材料的波后质点速度、波后压力、岩石中的冲击波速度及岩石的体应变分别为：

式中：ρ为铜的初始密度，ρ=8 930 kg/m；、为铜的材料参数，=3 940 m/s，=1.49；ρ为花岗岩的初始密度，其值通过密度实验获得：ρ=2 686 kg/m。

实验时准备并安装好弹丸、电探针、靶板和DISAR 系统。利用压缩空气（设计冲击速度小于400 m/s）或压缩氮气（设计冲击速度大于400 m/s）推动弹丸高速撞击靶板。为了拟合花岗岩的-曲线，共设计了4 种撞击力水平，并各重复3 次实验。由式（12）～（15）获得各状态量的结果，见表5。基于实验数据拟合花岗岩试件的-曲线，其形式如式（7），拟合结果如图9 所示，拟合得到的-方程为：

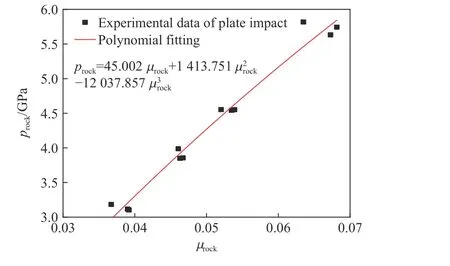
图9 拟合的花岗岩prock-µrock 曲线Fig. 9 Fitting curve of plate impact data of granite samples

表5 花岗岩平板撞击实验结果Table 5 Plate impact test results of granite samples

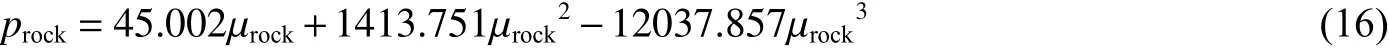
式中：的单位为GPa。因此状态方程相关参数、、的值分别为：=45.002，=1 413.751，=-12 037.857。

综上所述，花岗岩的KF 模型参数已被确定，见表6。

表6 花岗岩KF 模型参数拟合结果Table 6 Fitting results of KF model parameters of granite

4 花岗岩侵彻实验及仿真验证

为了验证实验确定的花岗岩KF 模型参数值适用性，开展了花岗岩侵彻实验，并利用代入了实测参数值的KF 模型对侵彻实验进行模拟，进一步对比仿真与实验得到的最终侵彻深度与成坑结果。

4.1 侵彻实验

花岗岩侵彻实验基于 ∅ 30 mm 口径滑膛火炮开展，实验原理是利用火药气体燃烧产生的能量推动弹体侵彻岩石靶体。设计工况为子弹以约670 m/s 的速度侵彻半无限厚靶体。

考虑到弹体发射的稳定性和岩石靶体取样大小的可操作性，本次实验采用次口径发射技术，利用直径20 mm、CRH 为2.5 的尖卵形头部杆形弹，外置直径30 mm 的三瓣式弹托进行实验，弹体材料为超高强度合金钢30CrMnSiNi2A，力学性能指标及Johnson-Cook 本构参数见表7。为了模拟半无限条件，需要合理设计靶体直径以忽略边界效应。当侵彻速度为670 m/s 时，由已有的研究成果可知，若靶弹径比不小于30，则可以忽略有限边界效应。将满足需求的600 mm×600 mm×800 mm 的花岗岩块放置在∅1 200 mm×800 mm 的钢套筒正中位置，并在空隙处浇筑C40 混凝土振捣填实养护28 d 制成靶体。

表7 弹体材料参数[28]Table 7 Parameters of the projectile’s material[28]

实验系统现场布局如图10 所示，整个系统主要包括3 部分：发射平台、测速系统和高速摄影系统。其中发射平台为口径30 mm 的滑膛火炮；测速系统用于获取子弹的侵彻速度，方法是通过在炮口和目标靶之间设置两道已知距离的测速靶纸，当弹体击穿靶纸时将分别输出2 个电信号至测速仪，根据信号的时间差即可获得弹体的平均飞行速度。根据测得的飞行速度可进一步调整火药的填装量，以实现设计的发射初速。高速摄像系统用于观察子弹的脱壳情况，并判断弹体入射姿态是否满足垂直入射要求。

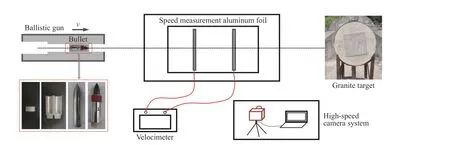
图10 侵彻实验装置布局图Fig. 10 Device layout diagram of penetration test

进行多次侵彻实验，根据高速摄影图片选取子弹侵彻着角小于5°的有效侵彻结果，图11 为3 个有效侵彻实验的弹坑照片与三维扫描结果。利用直尺和三维扫描仪对花岗岩侵彻后的靶体进行现场测量和光学扫描，测量及扫描得到的靶体侵彻深度及成坑参数见表8。

图11 花岗岩靶体弹坑照片及三维扫描图Fig. 11 Photos and 3D scanning results of cratering failure on the impact surfaces of granite targets

表8 花岗岩靶成坑参数现场测量及三维扫描结果Table 8 Direct measurement and 3D scanning results of crater parameters of granite targets

4.2 仿真与实验结果对比

利用LS-DYNA 对花岗岩侵彻实验进行仿真。考虑到实验的对称性，同时，为了减少计算成本，采用1/4 对称模型进行仿真实验，网格设计如图12 所示，将花岗岩靶体简化成了外套一圈薄层铁箍的∅1 200 mm×800 mm 的圆柱体，弹体则按实验中实用子弹进行建模，模型整体尺寸与实际实验中弹靶尺寸一致。

图12 侵彻实验数值模型Fig. 12 Numerical model

由于3 组实验测得的子弹侵彻速度接近，因此模拟时设置弹体在靶体中心处以670 m/s 的初速度垂直向下侵彻，弹体与靶体均采用实体单元网格，网格尺寸均设置为1 mm×1 mm×1 mm（弹头处网格做过渡处理）。靶体上表面设置为自由边界，下表面设置为无反射边界，靶体对称面上施加了对称边界。弹体和靶体间的接触采用*CONTACT_ERODING_SURFACE_TO_SURFA CE 接触算法定义。通过二次开发将KF 模型嵌入LS-DYNA 软件中，并作为靶体的材料模型，模型参数见表6。使用Johnson-Cook 模型作为弹体的材料模型，具体参数见表7。

提取靶体单元的损伤图像并进行对称处理，得到的靶体损伤分布如图13 所示。当损伤值为零时，表示单元未损伤，当损伤值为1 时，表示单元完全损伤。由图13 可知，计算得到的弹坑最大直径为400 mm，最小直径为300 mm。提取侵彻过程中子弹侵彻深度及加速度的历史曲线，如图14 所示，可以发现，侵彻深度达到约80 mm 时即保持不变，同时弹体的加速度时程曲线也呈现典型的三段式。

图13 靶体损伤分布情况及成坑参数Fig. 13 Damage distribution and cratering parameters of target

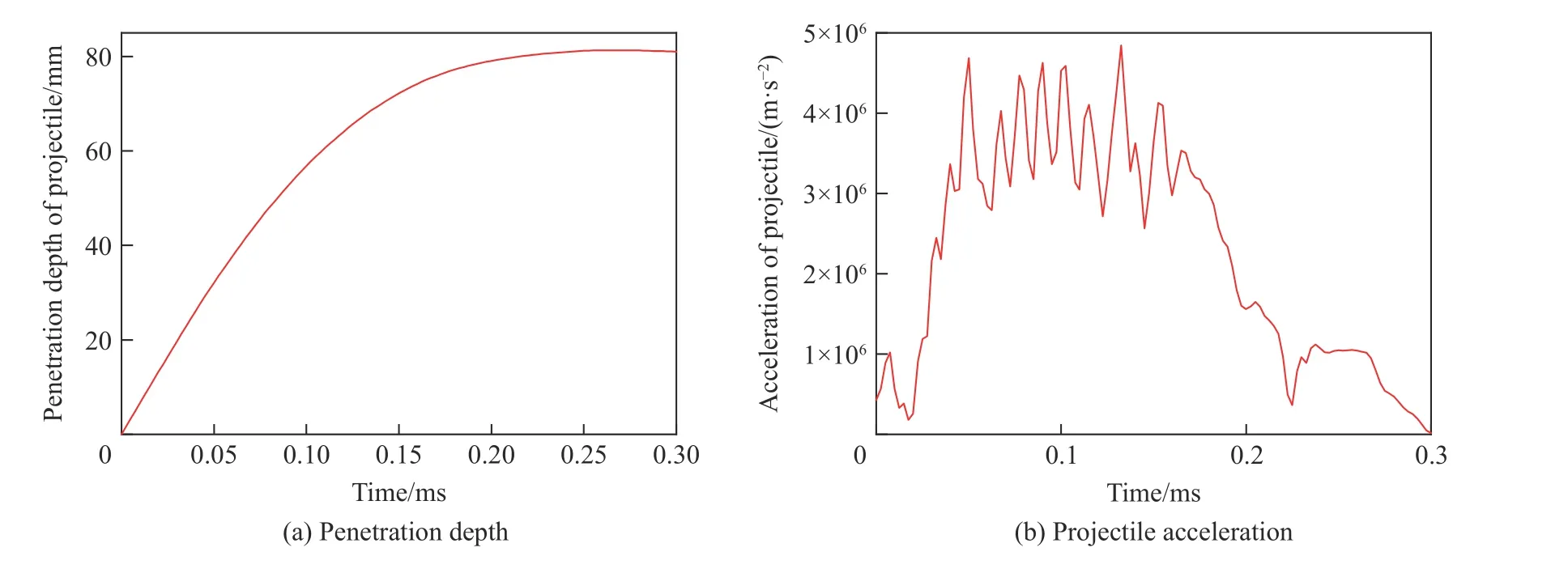
图14 弹体的侵彻深度和加速度时程曲线Fig. 14 History curves of penetration depth and acceleration of projectile

由于侵彻实验随机性较大，因此取成坑参数的平均值进行分析，结果见表9。对比实验和数值模拟得到的侵彻弹坑和侵彻深度发现，对于侵彻深度和弹坑最大直径，数值模拟与实验结果的误差小于5%；侵彻弹坑最小直径的模拟结果与实际结果误差较大，但仍小于15%。综上所述，采用KF 材料模型，并利用实验获取的参数值得到的数值模拟结果与实验结果吻合较好，验证了材料模型及实测参数值具有较好的适用性。