软质聚氨酯泡沫的动态压缩力学性能和本构模型*

苏兴亚，周 伦,2，敬 霖，邓贵德，赵隆茂

（1. 西南交通大学牵引动力国家重点实验室，四川 成都 610031；2. 四川航空工业川西机器有限责任公司，四川 雅安 625000；3. 中国特种设备检测研究院，北京 100029；4. 太原理工大学应用力学研究所，山西 太原 030024）

聚氨酯泡沫（polyurethane foam, PUF）作为一种高孔隙率的多功能材料，具有易于加工、高比强度、良好的能量吸收和缓冲隔振性能，被广泛应用于汽车工业、轨道交通、航空航天和包装工程等领域。根据其胞孔构型的不同，可分为闭孔型硬质聚氨酯泡沫（rigid polyurethane foam, RPUF）和开孔型软质聚氨酯泡沫（flexible polyurethane foam, FPUF）。PUF 作为民用工程防护材料时，服役过程中可能遭受的动态冲击作用情形如汽车碰撞、物体坠落等，通常为中应变率动态载荷。因此，研究中低应变率下PUF 压缩力学性能和本构关系，具有重要的学术和工程价值。

目前，针对聚氨酯泡沫的研究多聚焦于RPUF，且主要集中在准静态和高应变率加载情形。学者们开展了不同密度RPUF 的压缩力学性能实验，发现其静动态应力-应变曲线均表现出泡沫材料典型的三阶段特征，从细观层面揭示了不同压缩阶段胞孔的变形行为，并对其能量吸收特性进行了评估。结果表明，RPUF 具有一定的应变率敏感性和密度依赖性，其屈服应力和平台应力随应变率和密度的增加而增大，且高密度RPUF 的应变率敏感性更加明显。此外，准静态加载下RPUF 的能量吸收效率随密度的增加而减小，而高应变率加载下两者没有明显的关联性。在本构模型方面，一些学者基于黏弹性和黏弹塑性材料假设，提出了一系列可描述PUF 压缩力学响应的本构模型，并给出了材料的屈服准则，但是这些模型的参数较多且计算复杂，不便于工程应用。近年来，基于实验数据拟合的经验型和半经验型本构模型因具有使用方便、物理意义明确等优点被广泛发展和使用，如Rusch 模型、Sherwood-Frost (S-F)模型和Avalle 模型等。然而，对于中低应变率下FPUF 压缩力学性能和本构关系的研究还比较匮乏，其应变率敏感性和能量吸收特性还不够明确。

本文中，拟开展FPUF 的中低应变率压缩力学性能实验，分析其力学响应特征和应变率敏感性，并对其能量吸收特性进行评估；基于静动态压缩实验结果，通过引入应变率相关参数，构建可描述FPUF 应力-应变响应特征的修正S-F 模型和修正Avalle 模型。

1 实 验

实验选用由发泡工艺制成的开孔型FPUF，密度为0.176 g/cm，试件边长为50 mm，高为25 mm，如图1(a)所示。图1(b)给出了FPUF 的细观结构图，其中胞孔呈圆形或椭圆形且均匀性良好，胞孔之间通过胞壁孔隙实现相互连通，其平均孔径为0.35 mm，材料的平均孔隙率为0.84。采用DDL-200 电子万能试验机开展了应变率为0.001 和0.01 s时FPUF 的准静态压缩力学性能实验，压缩应变均大于80%。采用Instron 9350 落锤试验机开展40、70 和100 s等3 种应变率下FPUF 的动态压缩力学性能实验。落锤总质量为9.993 kg，选取直径为100 mm 的钢质圆形锤头。实验时锤头分别在0.051、0.156 和0.919 m 高度自由下落以实现3 种应变率加载，对应的冲击能量分别为4.997、15.302 和31.228 J，锤头定位精度为±1 mm。图2 给出了准静态和动态压缩实验装置及相关实验细节。为了保证实验结果的可靠性，每种应变率下均开展3 次有效重复性实验，选择最接近平均值的应力-应变响应曲线进行应变率敏感性和能量吸收特性分析。

图1 FPUF 试件尺寸和SEM 图像Fig. 1 The specimen size of FPUF and its SEM image

图2 准静态和动态压缩实验装置Fig. 2 Equipment for quasi-static and dynamic compression experiments

2 实验结果与讨论

2.1 应力-应变响应

图3 为FPUF 的静动态压缩应力-应变曲线，可以看出，相同应变率下3 次实验的应力-应变曲线重复性较好，说明实验结果具有较高的可信度。不同应变率下材料均表现出三阶段（弹性段、平台段和密实化段）变形特征，其压缩应力随应变的增大逐渐提高。这是因为：在压缩变形初期，沿加载方向较大的胞孔首先发生弹性挤压变形，此时应力随应变的增大呈线性提高；当试件继续被压缩时，已变形胞孔周围的胞壁也逐渐发生弯曲和扭转，导致该胞孔变形加剧并在其附近形成坍塌区，材料由弹性段逐渐进入到平台段，而坍塌区数量随试件压缩变形量的增加不断增加，宏观上表现为平台段应力随应变的增大缓慢提高；随着试件压缩变形加剧，大量胞壁之间产生接触并不断相互挤压导致应力迅速增大，材料逐渐进入到密实化段。对比发现，准静态加载下应力-应变曲线中的平台段相对较长，而动态加载下平台段随应变率的升高明显变短。与RPUF 不同的是，本文中FPUF 在卸载后试样的压缩变形几乎可以完全恢复，而RPUF 则会产生永久变形或破坏。

图3 在不同应变率下FPUF 的压缩应力-应变关系Fig. 3 Compressive stress-strain curves of FPUF at different strain rates

密实化应变ε是表征泡沫材料压缩变形能力的重要参量，其确定方法主要有经验法、切线法和能量吸收效率法。经验法假设ε与材料的相对密度 ε=-ρ¯ 线性相关，其计算方法为 ε=-ρ¯ ，其中和为材料参数。切线法认为应力-应变曲线中平台段切线和密实化段切线交点对应的应变为密实化应变。能量吸收效率法把最大吸能效率η对应的应变认为是密实化应变。经验法仅适用于准静态加载工况，而切线法获得密实化应变的过程较复杂，因此本文中采用能量吸收效率法计算ε。在任意给定压缩应变ε下，材料的吸能效率η(ε)为：

式中：σ(ε)为应变ε 对应的应力，σ为应变ε对应的应力。图4 为应变率为0.001 s时FPUF 典型的吸能效率图，可知，η(ε)随工程应变的增大先升高后降低，此时ε的计算方法为：

图4 0.001 s-1 应变率下FPUF 的压缩应力和吸能效率随应变的变化Fig. 4 Variation of compressive stress and energy absorption efficiency of FPUF with strain at the strain rate of 0.001 s-1

从图3 可以看出，FPUF 平台段应力σ随应变的增大有所提高，很难从应力-应变曲线中直接得到其具体数值。因此，可基于能量吸收原理计算得到：

2.2 应变率效应

图5 为不同应变率下FPUF 密实化应变的计算结果。可以看出，随着应变率的升高，准静态加载下材料的密实化应变相差不大，而动态加载下其密实化应变显著减小，高密度PUF和闭孔泡沫铝也具有相同的特性。不同应变率下FPUF 的平台应力和屈服应力如图6 所示，其中平台应力根据式(3)计算获得，屈服应力为应力-应变曲线中弹性段切线和平台段切线交点对应的应力。由图可知，FPUF 的平台应力和屈服应力随应变率的升高而提高，材料表现出应变率强化效应。此外，以铝（aluminum, Al）、丙烯腈-丁二烯苯乙烯（acrylonitrile butadiene styrene, ABS）、聚乙烯（polyethylene, PE）、聚对苯二甲酸乙二醇酯（polyethylene terephthalate, PET）和聚甲基丙烯酰亚胺（polymethacrylimide, PMI）为基体泡沫材料的平台应力也出现相同的规律，如图7 所示。其中材料的密度（单位：g/cm）已在图中标注，如FPU (0.176)表示密度为0.176 g/cm的软质聚氨酯泡沫。对比发现，相同应变率下FPUF 具有较低的平台应力，随着应变率 ε˙ 的升高，不同泡沫材料的应变率敏感性也有所不同。

图5 不同应变率下FPUF 的密实化应变Fig. 5 Densification strain of FPUF at different strain rates

图6 不同应变率下FPUF 的平台应力和屈服应力Fig. 6 Plateau stress and yield stress of FPUF at different strain rates

图7 不同泡沫材料的平台应力与应变率之间的关系Fig. 7 Relationships between plateau stress and strain rate for different foams

在给定应变下，可用应变率敏感性指数表征泡沫材料塑性应力的应变率敏感程度：

式中： ε˙ 和ε ˙分 别为实验 应 变 率和参考 应 变 率，σ 和σ分别为对应的应力，本文中参考应变率取0.001 s。图8 给出了动态载荷下FPUF 的应变率敏感性指数与应变之间的关系，可以看出，不同工况下均为正值且随应变率的升高逐渐增大，表明材料具有明显的应变率强化效应。此外，当应变率为40 和70 s时，在较小应变下FPUF 的应力升高较慢，此时随应变的增大逐渐减小，当应变达到0.2 时，材料的应力随应变的增大有较大幅度的提升，从而使得有所增大；当应变率为100 s时，材料的应力随应变的增大显著提高，导致随应变的增大逐渐增大。高分子聚合物泡沫应变率效应产生的主要原因有3 个方面：(1)基体材料的应变率敏感性；(2)胞孔的微惯性效应；(3)胞内气体的黏性流动。FPUF 的基体为高分子聚合物，是一种应变率敏感性材料，动态加载下其压缩力学响应大于准静态结果，导致FPUF 表现出应变率强化效应。此外，高应变率下胞孔的微惯性效应会抑制其屈曲变形，使得材料的应力升高。随着压缩速率的升高，泡沫材料在塑性变形过程中胞孔内的空气迅速被压缩，而压缩空气无法在短时间内从胞孔内全部流出，导致气体的黏性流动阻力增大，该现象在闭孔泡沫材料内更显著，宏观上表现为高应变率下材料出现较高的压缩应力。

图8 动态压缩下FPUF 的应变率敏感性指数与应变之间的关系Fig. 8 Relationship between strain rate sensitivity index of FPUF and strain under dynamic compression

2.3 能量吸收

泡沫材料的压缩应力-应变曲线中通常存在低应力平台，导致材料能够在较低的应力水平下吸收大量能量，当应变为ε时单位体积材料吸收的能量可表示为：

图9 为不同应变率下单位体积FPUF 吸收的能量随应变的变化，可以看出，随应变的增大不断增大且表现出明显的应变率强化效应。当泡沫材料压缩至密实化应变后，其压缩应力随应变的增大迅速提高，因此当用于缓冲防护时通常希望材料在密实化应变之前吸收大部分冲击能量。不同应变率下单位体积FPUF 在密实化应变时吸收的能量如图10 所示，由图可知，随应变率的升高逐渐增大，表明高应变率下FPUF 的能量吸收值更大。

图9 不同应变率下单位体积FPUF 吸收的能量随应变的变化Fig. 9 Variation of energy absorbed per unit volume of FPUF with strain at different strain rates

图10 单位体积FPUF 在密实化应变时吸收的能量随压缩应变率的变化Fig. 10 Variation of energy absorbed per unit volume of FPUF at densification strain with compressive strain rates

图11 不同应变率下FPUF 的最大吸能效率和最大理想吸能效率Fig. 11 The maximum energy absorption efficiencies and the maximum ideal energy absorption efficiencies of FPUF at different strain rates

比吸能是评价泡沫材料吸能特性的另一个重要指标，定义为单位质量材料所吸收的能量：

式中：ρ 为材料的密度。

为了研究比吸能随应变率的变化规律，本文中选择应变为0.4 时材料的比吸能进行分析，如图12 所示。可以看出，随着应变率的升高，准静态加载下FPUF 的比吸能相差不大，当应变率高于0.01 s时其比吸能显著提高。此外，图中还对比了以乙烯-醋酸乙烯聚合物（ethylene-vinyl acetate copolymer, EVA）、发泡聚乙烯（expanded polyethylene, EPE）、二氧化硅增强聚氨酯（silica reinforced polyurethane, PU/SiO）和陶瓷填充聚氨酯（ceramic filled polyurethane, PU/C）为基体泡沫材料在压缩应变为0.4 时的比吸能。可以看出，由于不同材料压缩力学响应具有不同的应变率敏感性，导致其比吸能随应变率的变化趋势有所不同。此外，与图中其他材料相比，准静态加载下FPUF 的比吸能相对较小。当应变率升至100 s时，由于此时FPUF 已进入密实化段，材料所吸收的能量迅速增大，导致其比吸能显著提高。

图12 不同泡沫材料的比吸能与应变率的关系Fig. 12 Relationship between specific energy absorption of different foams and strain rate

3 本构模型

泡沫材料通常具有细观结构多样、胞孔大小不均等特点，导致从微尺度层面构建其本构模型较复杂，目前研究者主要结合宏观力学性能实验来研究其本构关系。其中，以S-F 模型为代表基于实验结果的经验型本构模型和以Avalle 模型为代表半经验型本构模型被广泛使用。由图8 可知，FPUF 具有应变率强化效应且应变率敏感性指数受应变和应变率的耦合影响，而S-F 模型中材料的应变率敏感性指数只与应变线性相关，Avalle 模型仅适用于准静态加载工况，为了准确描述不同应变率下材料的应力-应变响应，需对模型进行修正。

3.1 Sherwood-Frost 修正模型

为了准确描述率温耦合下泡沫材料的压缩力学响应，在Nage 模型的基础上，通过引入环境温度和材料密度相关参量，Sherwood 等提出了考虑多因素影响的S-F 模型，材料的应力σ 为：

式中：、和分别为实验温度、参考温度和环境温度；、、、A、和为待定参数。因本文实验均在室温下开展且材料密度不变，()和(ρ)均取1。从式(12)可以看出，形状函数(ε)为应变的级数，且越大拟合精度越高，但同时会增加计算量，因此使用该模型时应充分平衡精度和计算量之间的关系。利用最小二乘法，通过对应变率0.001 s时FPUF 的实验结果进行拟合，发现当=8 时便达到很好的预测效果，如图13 所示，此时形状函数(ε)的参数值见表1。

表1 形状函数 f(ε) 的参数Table 1 Fitting parameters of the shape functionf(ε)

图13 S-F 模型的预测结果和实验结果的对比Fig. 13 Comparison of the prediction by the S-F model with the experimental result

研究表明，利用式(13) 得到的拟合结果和FPUF 的实验数据整体上差别较大。为了准确描述静动态加载下材料的应力-应变响应，基于压缩实验结果，把应变率项修正为：

图14 对比了模型预测和实验结果，可以看出，修正后的S-F 模型可以很好地表征不同应变率下FPUF 的压缩应力-应变响应。

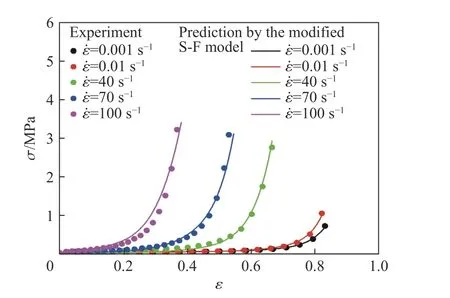
图14 修正后的S-F 模型的预测结果和实验结果的对比Fig. 14 Comparison of the predictions by the modified S-F models with the experimental results

3.2 Avalle 修正模型

式中：和分别为材料的弹性模量和平台应力，、和为应变相关参数。以0.001 s为参考应变率，此时FPUF 的弹性模量和平台应力分别为0.168 和0.019 6 MPa。利用最小二乘法，对实验结果进行拟合，得到Avalle 模型的表达式（σ 的单位为MPa）为：

图15 为准静态加载下Avalle 模型的预测结果与实验结果的对比，可以看出两者吻合较好，然而该模型没有考虑应变率的影响。为了准确描述不同应变率下FPUF 的压缩应力-应变响应，通过在式(18)右侧乘以式(14)所示的应变率项对Avalle 模型进行修正，并利用最小二乘法进行数据拟合，得到修正的Avalle 模型（ σ 的单位为MPa）：

图15 Avalle 模型的预测结果与实验结果的对比Fig. 15 Comparison of the prediction by the Avalle model with the experimental result

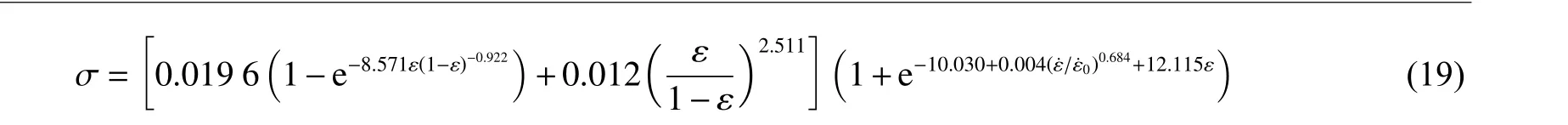
图16 为修正的Avalle 模型的预测结果与实验结果的对比，可以看出，修正后的Avalle 模型可以很好地表征应变率对FPUF 应力-应变响应的影响。与修正的S-F 模型相比，修正后的Avalle 模型参数较少且其中和的物理意义明确，便于工程应用。

图16 修正后的Avalle 模型的预测结果与实验结果的对比Fig. 16 Comparison of the predictions by the modified Avalle model with the experimental results

4 结 论

利用万能试验机和落锤试验机研究了0.001～100 s应变率范围内软质聚氨酯泡沫的压缩力学性能，分析了其应力-应变响应特征和应变率敏感性，讨论了应变率对其应变率敏感性指数和能量吸收特性的影响，建立了可准确表征材料静动态压缩力学响应的本构模型，获得的主要结论如下。

(1)静动态加载下，软质聚氨酯泡沫的应力-应变响应表现出弹性段、平台段和密实化段的三阶段特征，材料具有明显的应变率强化效应，且应变率敏感性指数受应变率和压缩应变的耦合影响。

(2)准静态加载下，软质聚氨酯泡沫具有较高的能量吸收效率而能量吸收值较小，应变率对最大吸能效率和比吸能的影响较小；动态加载下，随着应变率的升高，最大吸能效率逐渐降低而比吸能明显升高，应变率为100 s时其比吸能显著高于其他加载工况。

(3)通过引入应变率相关参量，修正后的S-F 模型和Avalle 模型均能够很好地表征静动态压缩加载下软质聚氨酯泡沫的力学响应，但修正后的Avalle 模型的参数较少，更便于工程应用。