基于改进Dijkstra算法与时频域滤波的雷达目标识别

王彩云，姚 晨，吴钇达，王佳宁，李晓飞，黄盼盼

（1.南京航空航天大学航天学院，江苏 南京 210016；2.北京电子工程总体研究所，北京 100854）

0 引 言

在弹道导弹自由飞行段，弹头诱饵目标除质心平动外，还存在微动，瞬时微多普勒频率常用于描述目标的微动特征。Chen最早将微动与微多普勒的概念引入雷达观测中。

目前，国内外学者提出多种微多普勒特征提取算法。王义哲等将拍卖算法和小波分析相结合实现多目标的微多普勒分离。邵长宇和李飞等利用最近邻数据关联算法选取椭圆内统计距离最小的测量值为更新状态，提出了一种基于多目标跟踪的多分量微多普勒分离方法。文献［7］针对单分量信号，利用最大峰值法提取时频脊线特征，该方法抗噪性能较差。若回波信号类型已知，可利用Hough变换得到多个时频曲线参数，耗时且计算量大。文献［9］将动态规划最优路径的Viterbi算法用于瞬时频率提取，获得较好的结果。文献［10-12］提出使用改进的脊路重组算法对二维时频图中多分量瞬时频率依次进行提取。Wang等提出了一种基于改进蚁群优化（ant colony optimization，ACO）算法的方法。在建立三维时频图的基础上，根据微多普勒的变化规律，分离出对应于每个散射点的单个微多普勒曲线。陈帅等利用重排Gabor分布与Viterbi算法相结合的方法，获取目标散射点的时频曲线，对目标信号时频曲线拟合后进行频谱分析，完成目标运动类型分类。Ji等利用贝塞尔函数将章动锥形目标分解为高次谐波分量，通过散射源点多普勒频率的谐波分量的振幅项和初始相位项得到圆锥重心到散射点的距离与圆锥章动参数。

针对弹道中段具有不同微动形式的弹头诱饵目标，为了获得更高的目标识别率，本文采取改进Dijkstra算法与时频域滤波提取目标微多普勒脊线特征，应用于弹道中段真假弹头目标识别，仿真实验结果证明了本文算法的有效性。

1 改进Dijkstra算法结合时频域滤波的微多普勒特征提取

1.1 改进Dijkstra算法

路径长度函数表示为

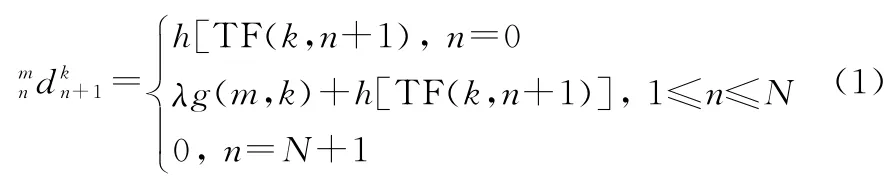
式中：函数（，）表征相邻时刻时频点的跳跃程度，确保微多普勒路径的连续性；函数（）函数衡量时频点TF（，＋1）的重要程度，确保微多普勒时频点的峰值性；为权重因子。

常见最短路径算法：蚁群算法、拍卖算法、Viterbi算法、Dijkstra算法。Dijkstra算法遍历所有节点寻找最短路径的最优解，计算量大、效率低。

为了减小算法复杂度，本文提出改进的Dijkstra算法，从时频点源点出发，向下一时刻时频点扩展，直到终点。该算法只需考虑相邻时刻的时频节点，基本步骤如下。

针对多分量回波信号，与最大峰值法相比，该算法既考虑到目标信号的峰值性，还考虑到时频脊线的连续性和平滑性。低信噪比下，减少选择噪声和其他分量时频点，抗噪性能较强。

1.2 时频域滤波

改进Dijkstra算法只提取多分量信号中最强分量的瞬时频率，利用时频域滤波对已提取的最强信号分量进行滤除，之后再利用改进Dijkstra算法继续提取强散射源的瞬时频率。

根据时频域滤波方法原理，设计时变带阻滤波器：

其中，为阻域。时频滤波后的时频图为

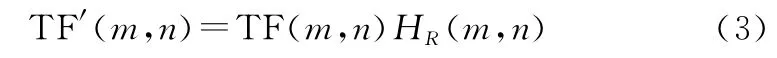
由目标信号在时频面上的支撑域推导出阻域的表达式：

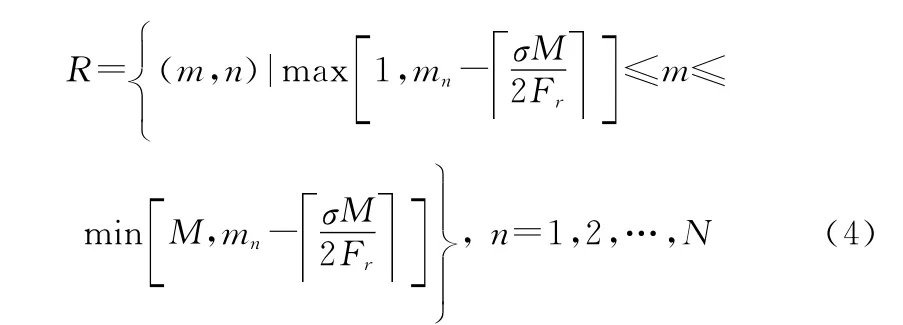
式中：F为信号载频；为时频分析的频率分辨率；表示向上取整。

基于改进Dijkstra算法与时频域滤波提取微多普勒特征步骤如下。

设目标回波信号经重排平滑伪魏格纳分布（reassigned smoothed pseudo Wigner-Ville distribution，RSPWVD）时频分析后得到初始时频图TFRS（，）。

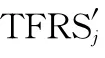
根据时频采样参数以及时频分析算法参数对时频点位置I （＝1，2，…，）与目标瞬时频率相对应，依次得到各分量信号的瞬时微多普勒特征。

2 基于微多普勒的弹道中段目标识别

在弹道导弹飞行中段，假设诱饵和弹头是几何外形尺寸相同的锥体目标，因为受力不同及弹头姿态控制，分别具有不同的微动形式，分别为进动弹头目标、章动弹头目标、摆动诱饵目标和翻滚诱饵目标，不同微动形式对雷达回波的调制特性不同，即各目标微多普勒特征不同。平动分量已完全补偿。

本节利用改进的支持向量机（support vector machine，SVM）分类器对具有不同微多普勒特征的弹道中段弹头和诱饵目标进行识别，具体步骤如下。

设定4种目标的微动参数范围，得到多组雷达基频回波信号。

采取本文算法依次提取目标各分量的微多普勒特征，将各分量特征串行构建联合微多普勒特征。

使用主成分分析方法对特征样本数据进行降维，按比例随机分成训练集和测试集。

初始化相关参数，利用训练集对改进SVM分类器模型进行训练。

利用训练好的SVM 分类器对测试集进行识别，输出各类目标分类的混淆矩阵。

3 实验仿真

3.1 实验数据介绍

仿真线性调频信号下雷达回波微多普勒。雷达信号参数为：采样频率PRF＝1 024 Hz，工作频率＝10 GHz，观察时间＝2 s。

目标坐标系中：锥顶和锥底散射点、和的坐标分别为：（0，0，2）、（0.3，0.4，-0.8）和（-0.3，-0.4，-0.8），单位为m。

雷达坐标系中：（，）＝（60°，45°），目标微动参数设置如下。

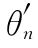
（2）进动：初始锥旋角φ＝0°，锥旋角速度ω＝2πrad／s，进动角＝15°。

（3）翻滚：初始翻滚角φ＝0°，翻滚角速度ω＝4πrad／s。

不同微动形式参数设置如表1所示。

表1 微动仿真参数设置Table 1 Micro-motion simulation parameters

根据表1的微动参数范围设置微动参数，每种不同微动形式的雷达目标各获取300组回波信号，根据本文第2节分别构建各目标特征样本数据库，按照1∶2的比例将特征样本随机分为训练集和测试集。

3.2 仿真结果与分析

以进动锥体弹头目标为例，按照第3.1节设置相关参数，进行对比试验。本文算法提取的目标强散射点回波的瞬时微多普勒分量与相应的理论值对比如图1（a）所示；Viterbi算法提取的目标强散射点回波的瞬时微多普勒分量与相应的理论值对比如图1（b）所示。其他两个分量提取结果与第一个分量类似，由于篇幅所限，本文省略。

图1 进动弹头目标强散射点回波微多普勒分量Fig.1 Micro-Doppler component of the strong scattering point echo from precessing warhead target

由图1可知，基于RSPWVD时频分析的进动弹头目标，利用本文微多普勒特征提取方法获得的估计值与理论值差别不大，很好地保存了回波信号的微多普勒特征，而Viterbi算法在交叉区域路径选择时出现频率跳变，无法准确地估计各频率分量。

为验证不同信噪比条件下该算法提取瞬时微多普勒特征的性能，进行100次蒙特卡罗仿真实验，用平均相对误差R 来衡量瞬时时频曲线估计值与理论值之间的偏差程度。

R 的具体表达式为

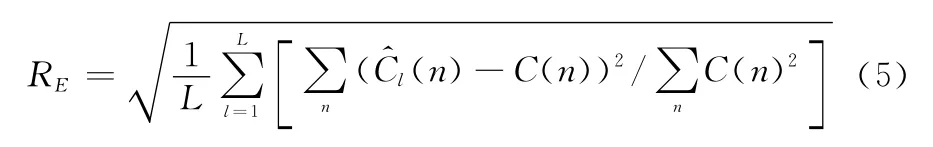
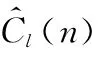
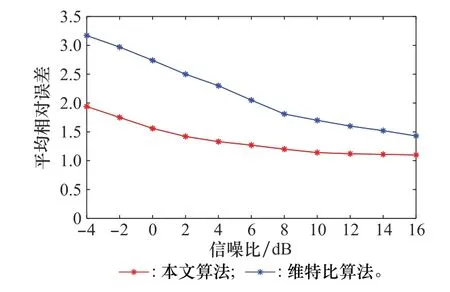
图2 不同信噪比下的平均相对误差Fig.2 Average velative error at different signal-to-noise ratios

由图2可以看出，在相同的信噪比下，本文方法的精度优于Viterbi算法。

为验证本文算法的识别性能，本节设计两组实验：实验1是在不同特征提取算法提取微多普勒特征用于目标识别；实验2是研究不同信噪比对目标平均识别率的影响。

对比不同特征提取算法提取微多普勒特征下的目标识别率

对测试集加入信噪比为0 dB的高斯白噪声，针对进动弹头、章动弹头、翻滚诱饵、摆动诱饵4个目标，为了验证本文算法的有效性，对比其他5种不同微多普勒特征提取算法：三次样条插值（cubic spline interpolation，Spline插值）算法、加权均值频率算法（weighted average frequency algorithm，WAFA）、最大峰值算法、霍夫变换算法、维特比算法，结果如表2所示，每种算法进行10次目标识别实验。

表2 6种微多普勒特征提取算法的目标识别率Table 2 Recognition rates of six micro-Doppler feature extraction algorithms

由表2可知：

（1）相同算法条件下，针对弹头，章动目标相比进动目标平均识别率高，针对诱饵，翻滚目标相比摆动目标平均识别率高。可能是由于章动与翻滚运动剧烈，导致目标回波调制度较大，便于识别，而进动与摆动，目标回波的调制度小，导致识别率相对较低。

（2）Spline插值算法人为确定强散射源初始位置，存在一定的误差，导致目标平均识别率较低。WAFA算法是Hilbert-Huang变换的改进算法，该算法与最大峰值法都对噪声较为敏感，因此相同信噪比下目标平均识别率最低。

（3）与经典维特比算法相比，从图1可看出，本文算法在提取瞬时微多普勒脊线特征时在曲线交叉区域表现良好，因此获得更精准的微多普勒特征，其平均识别率比维特比算法高0.028 7。

（4）当信噪比为0 dB时，本文算法对弹头目标的平均识别率高达0.972 5，体现了该算法在提取微多普勒特征和真假弹头识别中的优越性能。

弹道中段目标识别的关键是识别真假弹头，进一步分析，弹头与诱饵的平均识别率对比结果如图3所示。

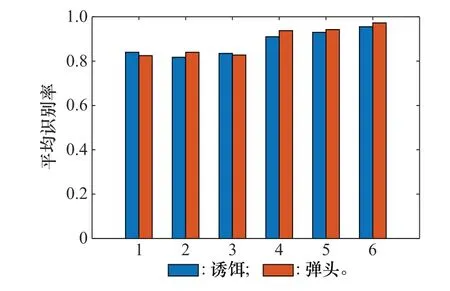
图3 6种微多普勒提取算法下诱饵与弹头的平均识别率Fig.3 Average recognition rates of decoy and warhead via six micro-Doppler extraction algorithms

其中，横坐标“1”代表Spline插值算法，“2”代 表WAFA算法，“3”代表最大峰值法，“4”代表霍夫变换，“5”代表维特比算法，“6”代表本文算法。

不同信噪比下对比不同微多普勒特征提取算法下的目标识别率

本实验中对测试集添加不同信噪比的高斯白噪声进行实验，设置信噪比范围为［-5，0，5，10，15］，单位为d B。仿真实验结果如图4所示。

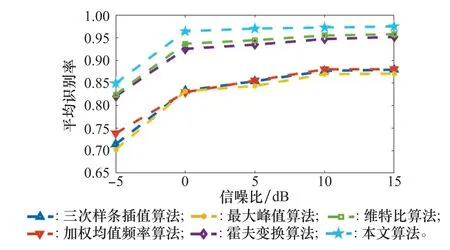
图4 不同信噪比下目标平均识别率Fig.4 Average target recognition rate via different signal-to-noise ratios

由图4可知，在相同的信噪比条件下，本文所提的算法识别概率较高；特别是在较低信噪比条件下，如-5 dB时，目标平均识别率仍达0.85；信噪比高于0 d B时，目标平均识别率均高于其他5种现有算法；信噪比高于5 d B时，平均识别率均达到0.97以上。

综上可知，该算法在提高识别准确率的同时，鲁棒性强。

4 结 论

针对如何有效提取多分量回波信号微多普勒特征进行弹道中段目标识别问题，本文将瞬时频率估计转化为寻找时频节点间最短路径问题，提出了基于改进Dijkstra算法与时频域滤波相结合的目标识别方法。首先，采取RSPWVD时频分析方法得到各目标时频图；然后，根据信号瞬时频率与时频脊线位置对应关系，利用本文算法对微多普勒特征进行提取；最后，利用改进SVM分类器对具有不同微动形式的弹道目标进行识别。实验结果表明，针对弹道中段弹头诱饵目标识别，本文算法最高平均识别率达0.97以上，同时鲁棒性较好。