基于粒子群优化的波束空间广义旁瓣相消算法
2022-10-10李浩洋向建军李志军
李浩洋,向建军,彭 芳,王 帅,李志军
(空军工程大学航空工程学院,陕西 西安 710038)
0 引 言
自适应阵列天线能够选择一组振幅和相位权重,并与输入信号相结合,产生一个人工控制的波束图,优化所接收到的期望信号。这种形式的阵列处理方法提高了信号处理的抗干扰性能。自适应波束形成技术正广泛应用于军事雷达、通信、导航等众多领域。
在实际应用中,为了获得更好的分辨率和抗干扰能力,通常使用大规模阵列天线,这就会导致算法运算量增加,成为实现自适应波束形成算法的瓶颈。算法的运算量通常来自于自适应自由度,为了降低算法的运算量,通常采用部分自适应自由度的方法。降秩自适应波束形成是一种常用的采用部分自适应自由度的方法,主要有特征分解类算法,包括主分量法、交叉谱估计法。在实际应用中,由于特征分解类算法复杂度较高,往往在实际工程中难以应用。针对此类问题,文献[5]提出了波束空间预处理的方法,通过对波束进行预处理,降低了运算空间的维度,有效减少了运算量并抑制干扰。进行波束空间预处理的关键在于确定转换矩阵,通常转换矩阵采用无数据约束的方法确定,但当旁瓣出现强干扰时,这种方法难以有效抑制。文献[7]和文献[8]提出了一种高效自适应波束域转化方法,能够根据接收数据及时更新转换矩阵,有效抑制干扰,但由于采用特征分解的方法会导致算法复杂度增加。本文针对上述问题,提出了一种简便的自适应波束域转化方法,不需要特征分解来求解转换矩阵,使算法更易实现。采用这种方法处理广义旁瓣相消(generalized sidelobe canceller,GSC)算法可以得到波束空间GSC(beam space GSC,BS-GSC)算法。
由于自适应波束形成需要求解复杂的非线性问题,利用传统的数学解析方法和数值优化往往难以取得期望效果。粒子群优化(particle swarm optimization,PSO)算法是一种具有全局搜索能力的非线性约束优化算法,具有很强的稳健性,适用于解决非线性优化问题。文献[10]提出的改进PSO算法应用在波束形成中,起到了降低旁瓣和加深零陷的效果,但是存在收敛早熟、易于陷入局部最优、搜索范围小等问题。文献[11]针对PSO算法易于陷入早熟等问题提出了压缩因子的方法,使PSO算法的收敛效率有效提升。PSO算法在阵元空间起到了较好波束形成的效果,但目前还没应用到波束空间中。本文提出了一种基于PSO优化的BS-GSC算法,该算法在保证波束形成效果的基础上显著降低算法的运算量,并通过粒子群寻优手段有效降低波束形成旁瓣,提高了算法在低快拍、强干扰条件下的波束形成能力。
1 信号模型及GSC算法基本原理
在均匀线阵平面内,假设有个不相关窄带信号从远场入射到个阵元中,阵元间距为,信号入射角为θ(=1,2,…,),在远场空间有一个期望信号()(其来波方向为)和个干扰信号S()(=2,3,…,+1)(其来波方向为θ),每个阵元中的加性高斯白噪声为()。本文考虑信源与阵列平面共面的情形。阵列接收数据矩阵可以表示为
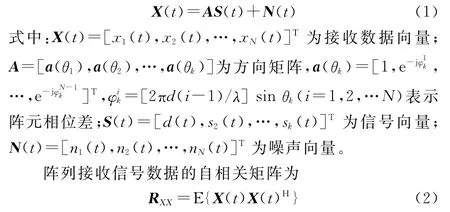
在实际情况中,由于接收的信号数据是有限的,接收数据是通过有限快拍数得到的,在有限快拍数下的自相关矩阵为
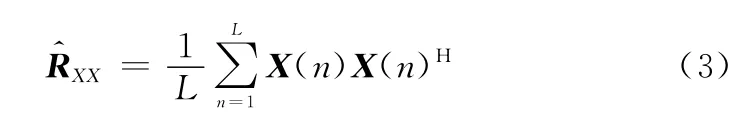
本文采用GSC算法对上述问题分析,其结构如图1所示。图1中,()为输入信号,()为输出信号。
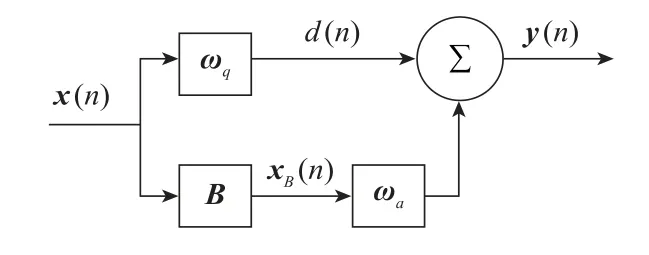
图1 传统GSC结构框图Fig.1 Structure block diagram of traditional GSC
GSC结构将信号分为两个支路,在上支路中ω为固定波束形成权矢量:
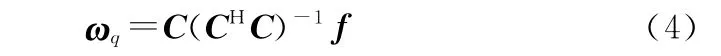
式中:=[(),(),…,(θ)]为约束矩阵;为相对应的约束响应矢量。
在下支路中,为达到阻塞期望信号的目的,通常在自适应权矢量ω前添加阻塞矩阵,阻塞矩阵需要满足=0。通过自适应权矢量ω让x ()逼近期望信号(),可以依据最小均方误差原则进行维纳滤波:
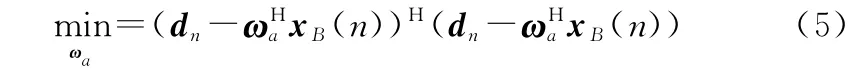
求得自适应权矢量ω为
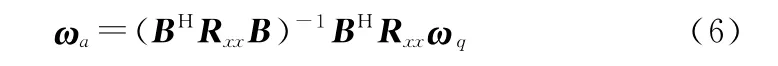
最终得到的GSC的权矢量可以写为

2 基于粒子群的BS-GSC算法原理与流程
2.1 BS-GSC算法
针对传统GSC算法在信号处理过程中阵元数量多,导致算法的运算量较大、运算时间长、复杂度高的问题,通常采用变换域的方法对阵列接收数据进行预处理,通过转换矩阵将信号处理过程由原本的阵元空间转换到空间相对较小的波束空间,从而减小了算法的运算量并提高了算法的稳健性。本文选取了一种简便的自适应波束空间变换方法,该方法可以根据接收数据自适应调整变换矩阵,有效地提高了运算效率。
首先选择(<)个正交波束,根据阵元导向矢量构建×的无数据约束转换矩阵。转化矩阵为
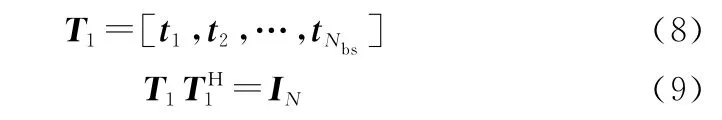
式中:I 为维单位矩 阵。
可以看作由个正交向量t (=1,2,…,)所张成的子空间。t 根据正交原理可以表示为
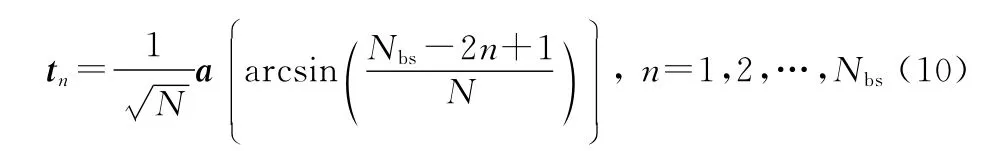
由以上公式可以推出:
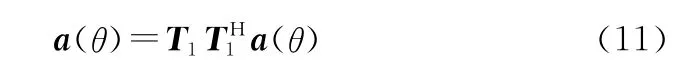
在保证期望角度范围内任意方向的响应均无失真的条件下,自适应调整转换矩阵,使输出总功率最小。本文采用最小输出功率原则,具体准则可以表述为
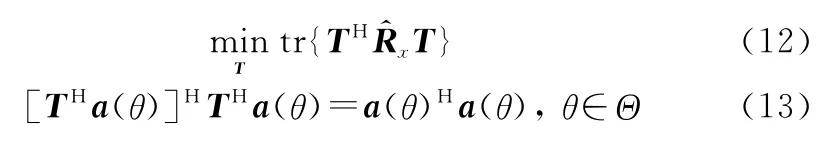
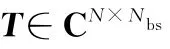
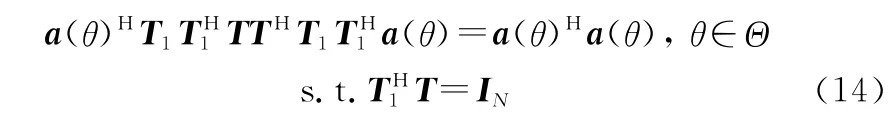
因此,最小输出功率准则可以转化为
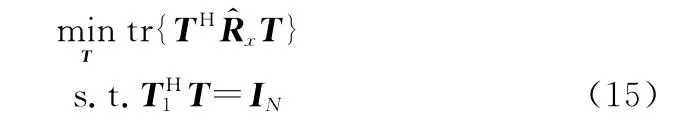
根据式(15)可以求得,转换矩阵的表达式为
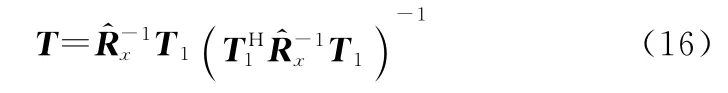
因此,波束空间信号数据()和导向矢量()可以表示为
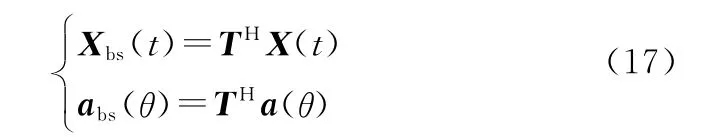
BS-GSC的其他变量可根据传统GSC原理求解,BSGSC框图如图2所示。
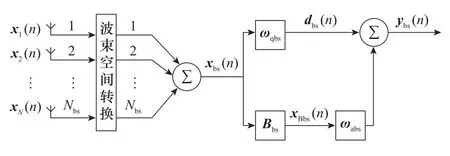
图2 BS-GSC结构框图Fig.2 Structural block diagram of BS-GSC
BS-GSC具体流程如下。
由式(16)确定转换矩阵,通过转换矩阵将阵元域信号数据()和阵列响应矢量()转换到波束空间,求得波束空间信号数据()和阵元响应矢量();
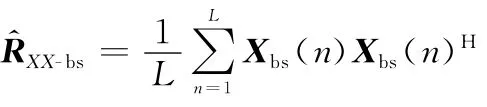
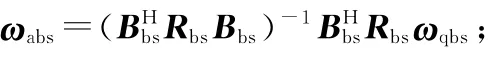
根据信号相消原理=-,求得GSC的最佳权矢量。
2.2 基于粒子群的BS-GSC算法
本节针对广义波束旁瓣相消器在低快拍情况下出现的不收敛和波束形成性能较差的问题,结合变换域原理,对信号数据进行全局搜索。在标准粒子群的算法基础上,通过引入压缩因子来加快粒子群的收敛性。
PSO是一种群智能算法,主要通过粒子间寻优与更新的迭代手段求得最优解。粒子的好坏由适应度函数来评价,在搜索解的过程中,每一个粒子都具有一组权值l 和一组权值更新速度向量v ,通过对粒子的权值与权值更新速度进行更新来得到最优解。本文通过PSO算法,以BS-GSC的自适应权矢量为变量,以输出最小均方误差为适应度函数、以输出最小均方误差为目标寻取最优解。定义适应度函数为
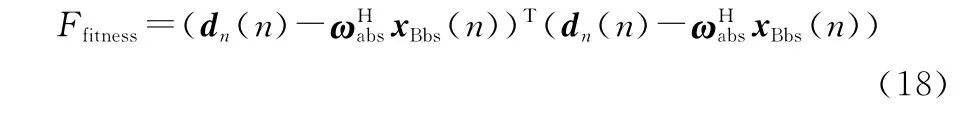
在空间内随机设置个粒子,进行第次迭代后,第个粒子的权值和权值更新速度分别为
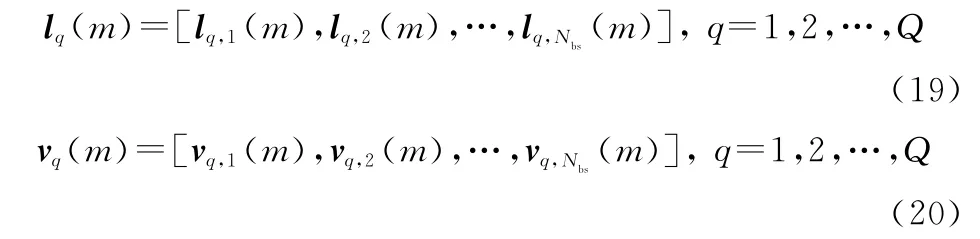
经过次迭代后,粒子的权值和权值更新速度均是经过多次优化的结果。继续迭代时,粒子会在自身的邻域内寻找适应度函数最佳的权值,并将邻域内的最优点与粒子局部最优点进行比较,将适应度函数最小的点作为粒子局部最优点,即
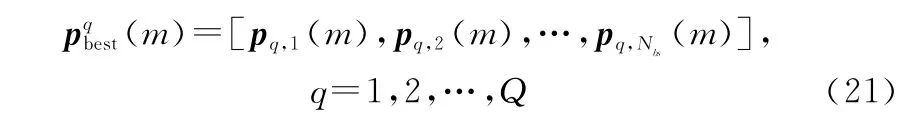
更新局部最优点后,比较所有粒子的局部最优点,并将适应度函数最小的点设为全局最优点,即

同时也增强了算法局部搜索能力,压缩因子粒子群算法权值更新速度和权值更新公式如下所示:
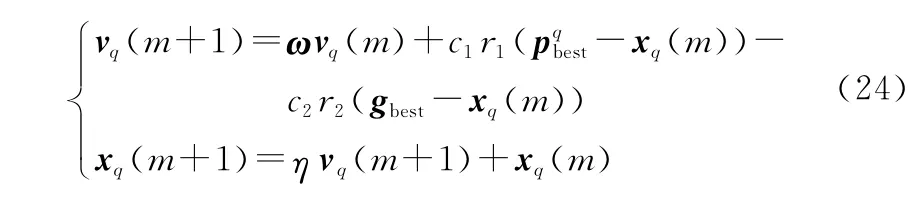
式中:表示压缩因子。
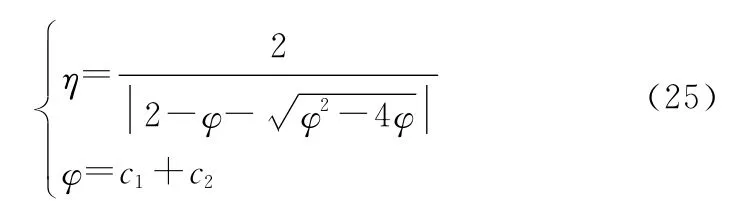
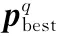
2.3 算法流程
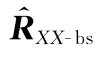
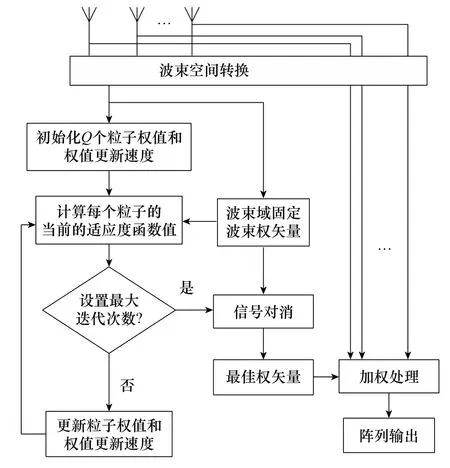
图3 基于PSO的BS-GSC框图Fig.3 Block diagram of BS-GSC based on PSO
在PSO算法中,设定每个粒子的维度与正交波束数量相同,粒子权值即为阵列权值,当循环次数达到最大迭代次数时算法终止,最大迭代次数通常与粒子数有关,粒子数量越大,算法收敛所需迭代次数越少。根据上述流程,本文算法计算步骤如下。
设定阵元数量为,快拍数为,正交波束数量为。
确定转换矩阵与阵元接收数据矩阵相乘得到波束空间信号接收数据()。
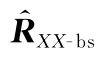
初始化粒子群,给定粒子群规模和循环次数,随机产生粒子初始权值l 和权值更新速度v ,其中粒子权值由波束空间自适应权矢量代替。
计算各粒子当前的适应度函数。
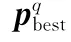
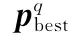
根据迭代次数重复步骤5~步骤7,输出最后一次的全局最优值,作为BS-GSC的自适应最优权系数。
据信号相消原理=-,求得GSC的最佳权矢量。
计算阵列的输出()。计算公式如下:
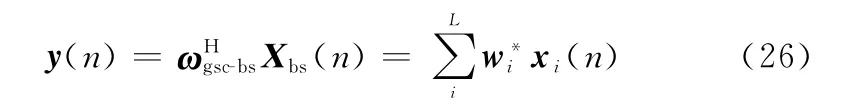
2.4 运算量和复杂度分析
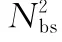
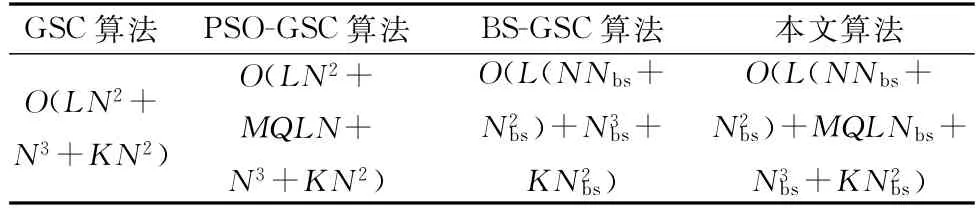
表1 算法运算量对比Table 1 Algorithm computation comparison
由表1可知,本文算法所在的波束空间相比于GSC和PSO-GSC的阵元空间(≪)数据维度减小,算法的自由度降低,算法的运算量和复杂度均减小,由于本文算法的所有运算都是在波束空间进行,因此整体运算量要小于以上两种算法,进行大规模阵列运算时实时性更好。由于本文算法采用粒子群寻优手段求取最优权值需要进行次迭代更新,运算量高于BS-GSC算法,但PSO算法采用最小均方误差准则迭代寻优,相对简单,算法复杂度较低。
3 算法仿真与分析
使用Matlab软件对本算法进行仿真模拟,原始数据为:阵元数=30,正交波束数量=10,期望信号角度=10°,干扰信号角=20°,=-20°,=60°,=-60°,粒子数为500,迭代次数为100,设定目标信号为带宽30 M Hz、中心频率为50 MHz的线性调频信号,干扰和噪声均为高斯白噪声。令信噪比(signal to noise ratio,SNR)为-10 dB,干噪比(jammer to noise ratio,JNR)为10 dB,快拍数=500。在上述条件下进行仿真分析。
3.1 阵列响应性能
图4的均匀线阵三维视图展示了阵列响应增益与快拍数和角度的关系。可以看出,本文提出算法的波束形成的主方向0°的阵列幅度为0 dB,可以精准地指向期望来波信号的方向,并在干扰方向产生了阵列幅度小于-120 dB的零陷,在4个干扰方向均形成了较深的零陷。通过阵列响应增益随快拍数的变化,可以看出本文算法虽然在极低快拍下会出现波形畸变的现象,但快拍数为20时,已经具有了良好的波束形成能力,因此本文算法在整体上具有良好的波束形成效果。
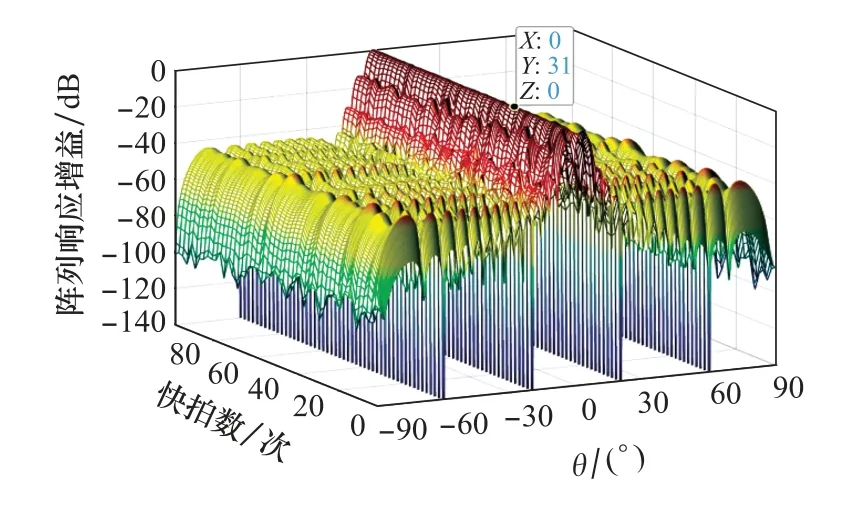
图4 均匀线阵三维波束图Fig.4 Three-dimensional beam pattern of uniform linear array
图5将本文算法与GSC、PSO-GSC和BS-GSC算法进行对比。可以看出,4种算法均在期望方向上形成了主瓣,且主瓣宽度近乎相同。其中,本文算法具有更低的旁瓣,主要是由于构造转换矩阵时,采用最小输出功率准则,自适应调整转换矩阵,在保证期望方向信号的增益不变的同时,使总输出功率降低,从而降低波束旁瓣。并且,本文采用PSO算法和最小均方误差准则,通过粒子的迭代更新逐渐缩小与期望信号的误差,进一步降低了波束旁瓣。
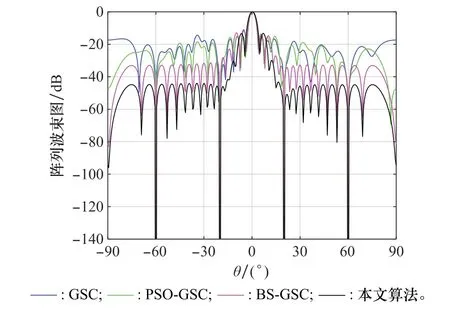
图5 波束形成对比图Fig.5 Comparison of beamforming
3.2 正交波束数量对本文算法的影响
在其他条件不变的情况下,将正交波束数量由8增加到17,得到波束形成方向图,如图6所示。由图6可以看出,随着正交波束数量的增加,波束的旁瓣略有降低,这主要是由于当波束数量增加时算法的自由度增加,使得算法的精度更高,效果更好。但是自由度的增加也会使算法的复杂度和运算量增加,因此确定正交波束数量时要选择合适的值。
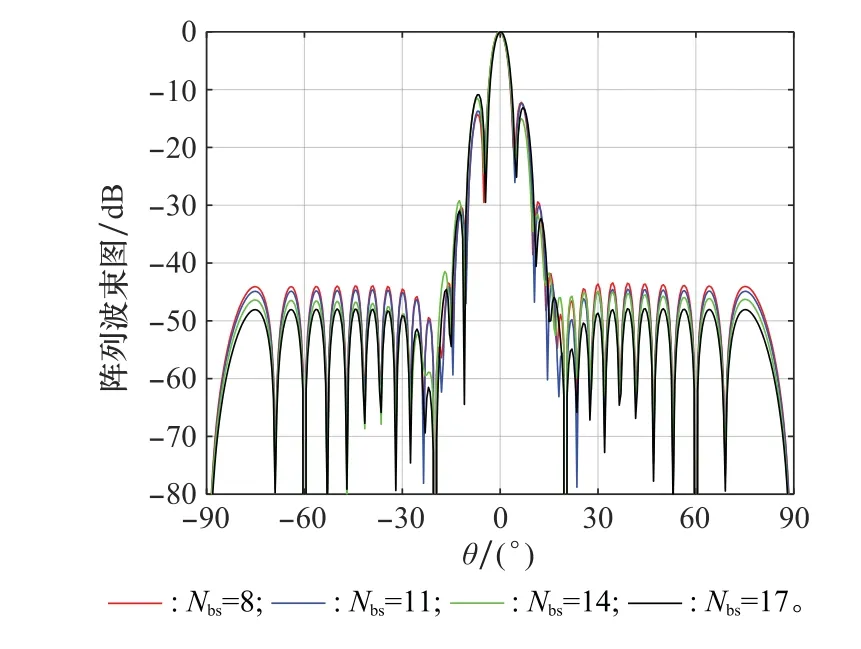
图6 本文算法在不同正交波束下的波束方向图Fig.6 Beam pattern of the proposed algorithm under different orthogonal beams
3.3 抗干扰性能分析
在其他条件不变的情况下,将JNR由-10 dB增加到150 d B,得到波束形成方向图,如图7所示。
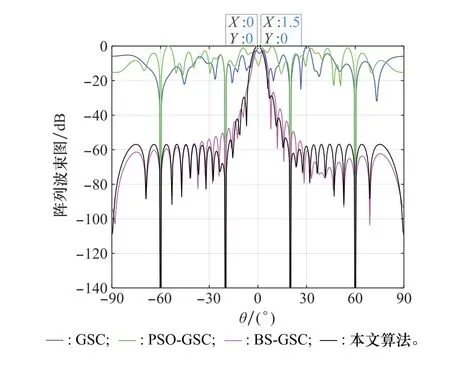
图7 JNR为150 dB时4种算法波束方向图Fig.7 Beam patterns of four algorithms when the JNR is 150 d B
由图7可以看出,当JNR增加时,4种算法的性能都会受到影响。由于干扰功率过强,GSC和PSO-GSC算法已经无法在期望方向上形成主瓣,BS-GSC算法可以正常形成主瓣但出现了1.5°的角度偏差。本文算法虽然主瓣变宽,但是仍可以在期望方向形成主瓣,可见在波束空间应用PSO算法,可以获得更好的干扰抑制效果。
在保持上述条件不变的前提下,设置JNR的区间为[-30,150]d B,对4种算法求解均方误差,得到图8所示的均方误差随JNR的变化曲线。由图8可以看出,4种算法在JNR低于140 dB时,均方误差稳定震荡;当JNR大于140 dB时,GSC均方误差随JNR的增加而迅速增加,其他3种算法的均方误差几乎保持不变;总体上看,BS-GSC和本文算法的均方误差值较小,PSO-GSC算法的均方误差略高于此两者算法。
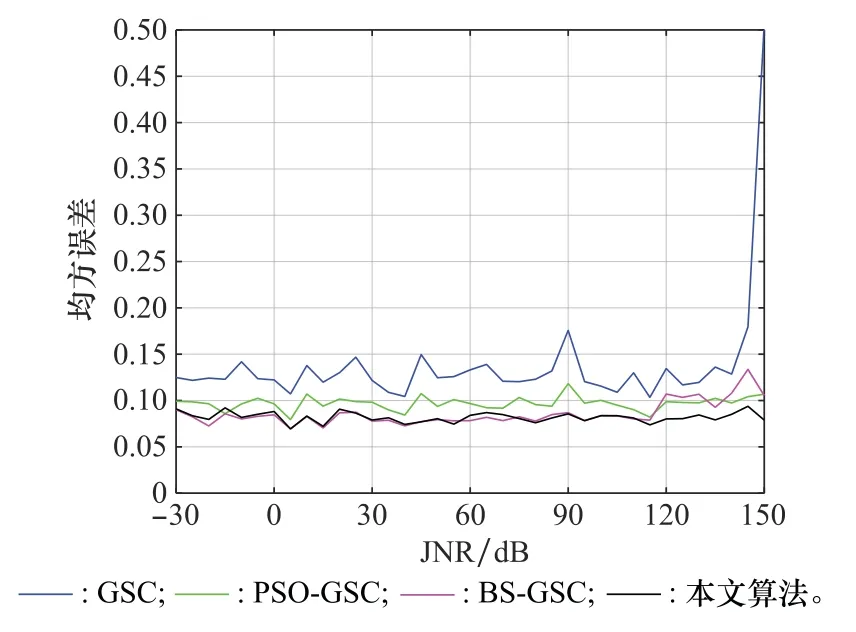
图8 不同JNR对4种算法影响Fig.8 Influence of four algorithms with different JNRs
为更好地探究快JNR对本文算法的影响,取JNR分别为0 d B、30 dB、60 dB、90 dB、120 d B,其他条件与上述一致,得到波束方向图如图9所示。
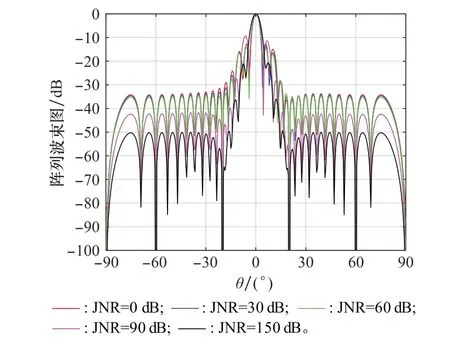
图9 本文算法在不同JNR下的波束方向图Fig.9 Beam pattern of the proposed algorithm under different JNRs
由图9所示,本文算法波束形成方向图的旁瓣随JNR增加而降低,但当JNR过大时,由于干扰功率过强,导致波束形成方向图的主瓣宽度增加,波束形成性能下降,信号的角度分辨率下降。总体上看,本文算法具有较好的抗干扰性能。
3.4 SNR对算法的影响
在其他条件不变的情况下,将信号的SNR由-10 dB增加到10 d B,得到波束形成方向图如图10所示。由图10可以看出,当SNR增加时,4种算法的性能都会受到影响,GSC、PSO-GSC、BS-GSC算法已经无法在期望方向上形成主瓣,这主要是由于当SNR增加时,期望信号的功率较大,导致阻塞矩阵不能完全阻塞期望信号,从而导致期望信号对消的现象。而本文算法虽然主瓣变宽,但是仍可以在期望方向形成主瓣,可见本文算法在抑制期望信号对消方面也有较大优势。
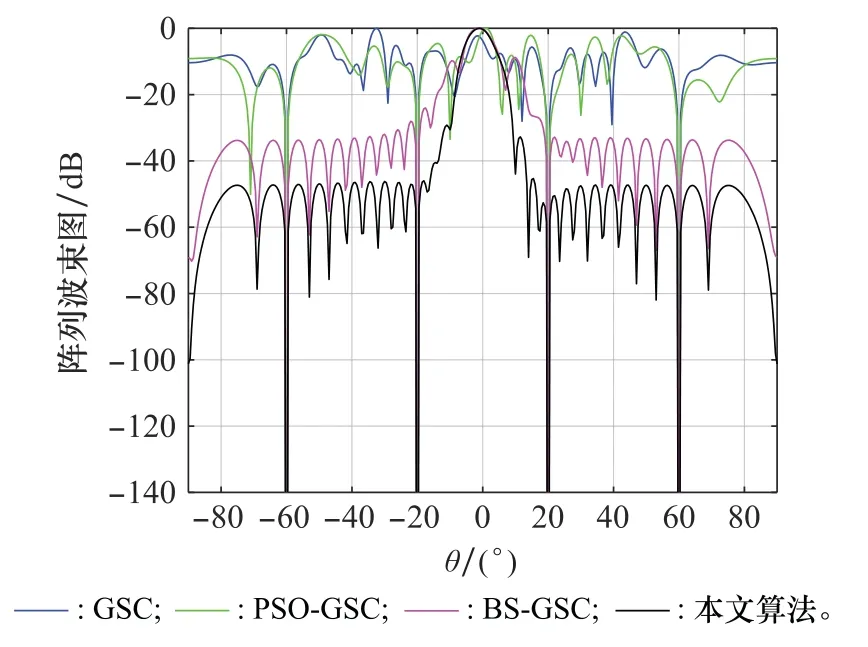
图10 SNR为10 dB时4种算法波束方向图Fig.10 Beam pattern of four algorithms when the SNR is 10 dB
在保持上述条件不变的前提下,设置SNR的区间为[-10,30]dB,对4种算法求解均方误差,得到如图11所示的均方误差随SNR的变化曲线。由图11可以看出,4种算法在SNR低于15 d B时,均方误差趋于零且平稳;当SNR在[15,25]dB时,GSC和PSO-GSC算法的均方误差随SNR的增加而增加,其他两种算法的均方误差几乎保持不变;当SNR大于25 dB时,4种算法的均方误差均随SNR增加而增加,GSC算法的均方误差增加得最快,PSO-GSC算法其次,BS-GSC算法和本文算法均方误差最小且增加速度相当。
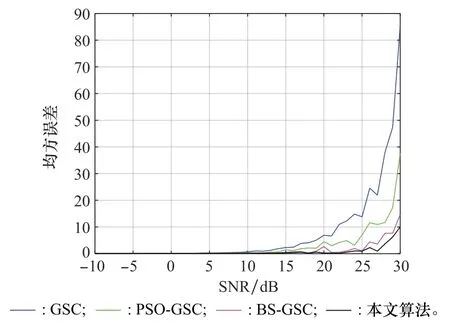
图11 不同SNR对4种算法影响Fig.11 Influence of four algorithms with different SNRs
为更好地探究SNR对本文算法的影响,取SNR为-20 dB、-10 dB、0 dB、10 d B、20 d B,其他条件与上述一致,得到波束方向图如图12所示。由图12所示,本文算法在SNR小于10 d B时,可以在期望信号方向形成主瓣。当SNR为20 d B时,由于期望信号相消导致无法在期望信号方向形成主瓣。由此可以看出,本文算法在一定程度上可以抑制期望信号相消,当SNR过大时,算法的波束形成性能会恶化。
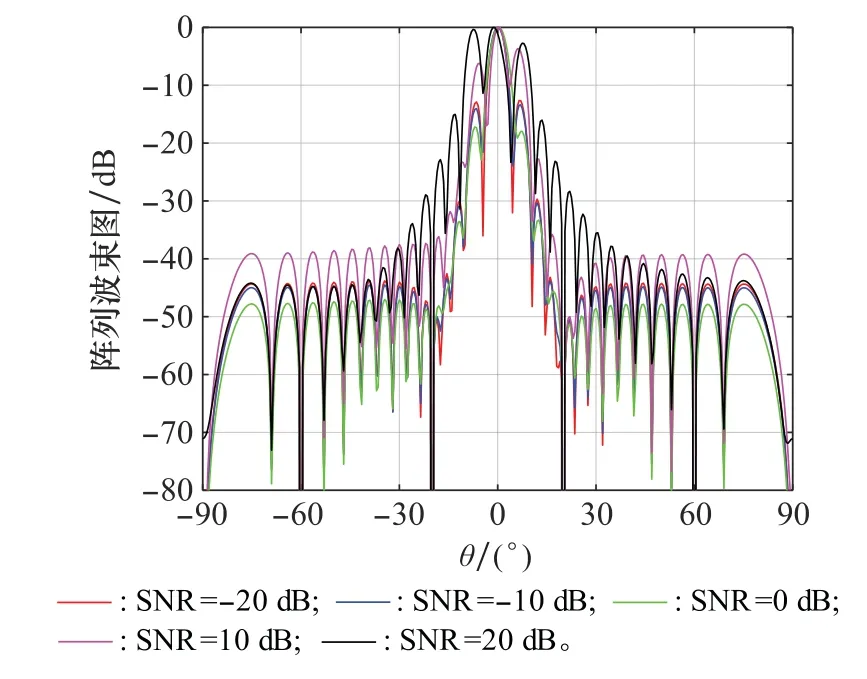
图12 本文算法在不同SNR下的波束方向图Fig.12 Beam pattern of the proposed algorithm under different SNRs
3.5 快拍数对算法的影响
在其他条件不变的情况下,将快拍数设定为20,得到波束形成方向图如图13所示。
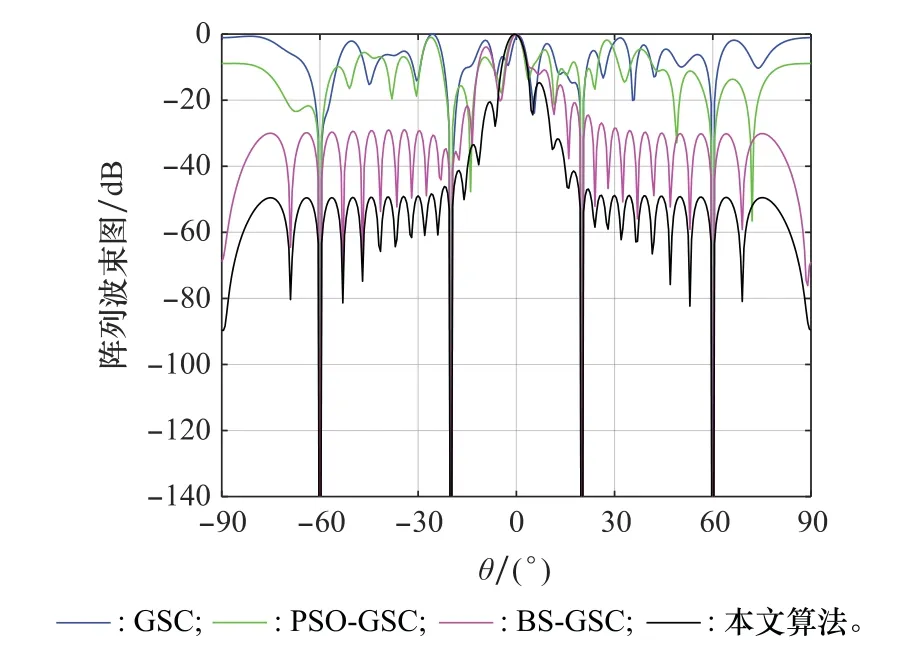
图13 快拍数为20时4种算法波束方向图Fig.13 Beam pattern of four algorithms when snapshot number is 20
由图13可以看出,在低快拍情况下,GSC算法已经无法在期望方向形成主瓣,波束方向图出现严重恶化,PSOGSC算法和BS-GSC算法可以正常形成主瓣,但是旁瓣电平升高,波束形成性能变差,导致虚警概率升高。本文算法依旧可以形成正常主瓣,但是主瓣宽度略有增加,旁瓣电平保持不变。由上可知,在低快拍的条件下,本文算法的期望信号波束指向和旁瓣抑制性能较好。
在保持上述条件不变的前提下,设置快拍数的区间为[0,400],对4种算法求解均方误差,得到如图14所示的均方误差随快拍数的变化曲线。由图14可以看出,4种算法的均方误差数值均随快拍数的增加而减小,其中传统GSC算法的均方误差大于其他3种算法。BS-GSC和本文算法的均方误差较小,在低快拍的条件下本文算法均方误差小于BS-GSC算法,当快拍数较高时,两种算法的均方误差数值趋于稳定且相近。
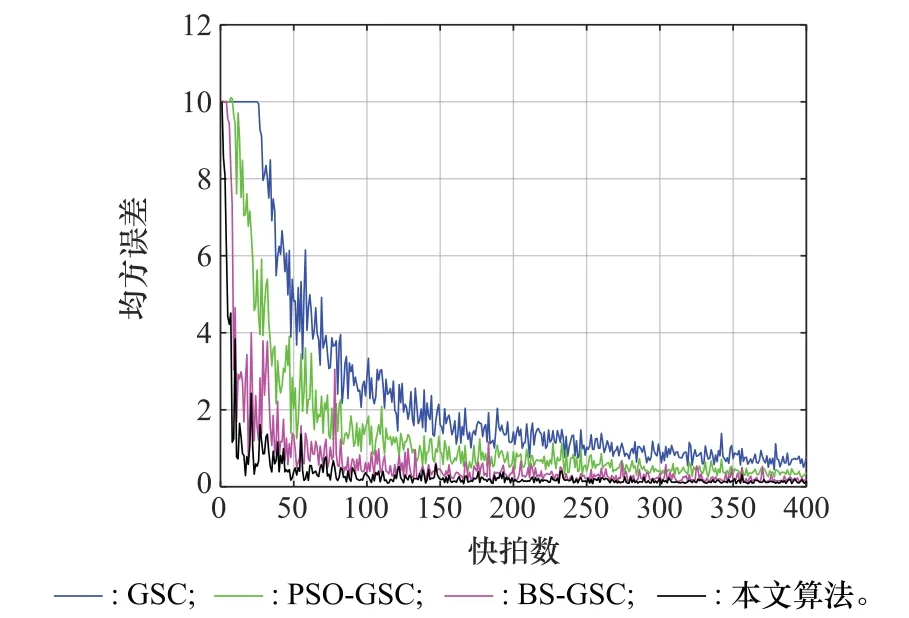
图14 不同快拍数对4种算法影响Fig.14 Influence of different snapshot numbers on four algorithms
为更好地探究快拍数对本文算法的影响,取快拍数分别为10、30、60、100、200,其他条件与上述一致,得到波束方向图如图15所示。
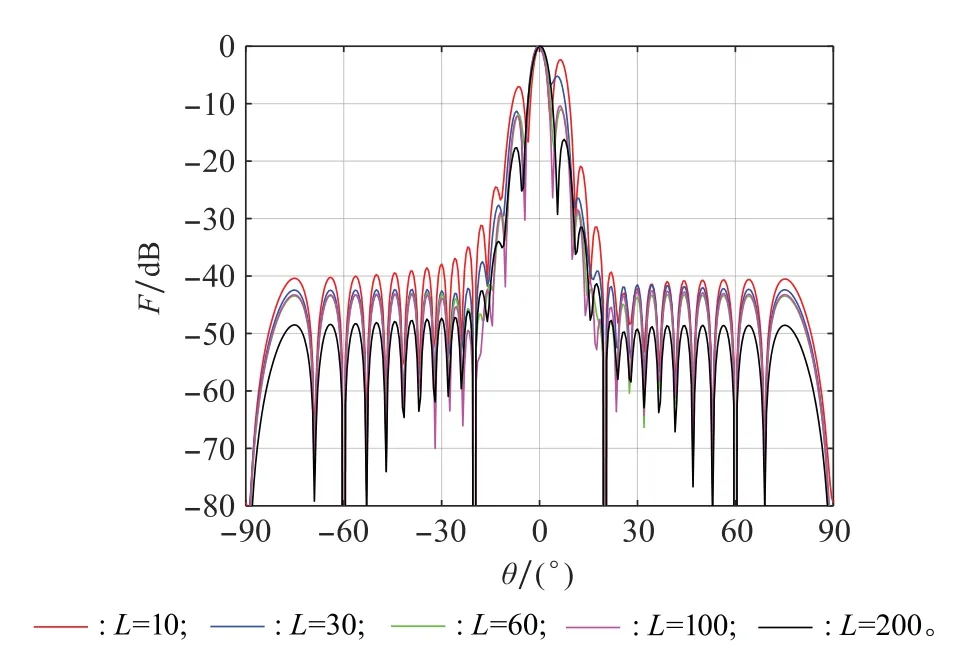
图15 本文算法在不同快拍数下的波束方向图Fig.15 Beam pattern of the proposed algorithm under different snapshot numbers
由图15可以看出,本文算法的旁瓣随着快拍数的增加逐渐降低,当快拍数为10时,旁瓣电平相对偏高,但仍然可以在期望信号方向形成主瓣,并且随着快拍数的增加波束旁瓣逐渐降低。可见本文算法在低快拍的情况下,依旧可以保持良好的波束形成能力。
3.6 来波方向对算法性能的影响
在其他条件不变的情况下,将信号的来波方向分别调整为:期望信号角度=0°,干扰信号角=3°,=-5°,=5°,=-3°和期望信号角度=0°,干扰信号角=5°,=-5°,=10°,=-10°,由图16和图17可知,当干扰方向与期望信号方向较近时,4种算法可以在期望方向形成主瓣,但当干扰进入主瓣方向时,4种算法均无法在期望信号方向形成主瓣,因此本文算法的抗主瓣干扰能力仍需提高。
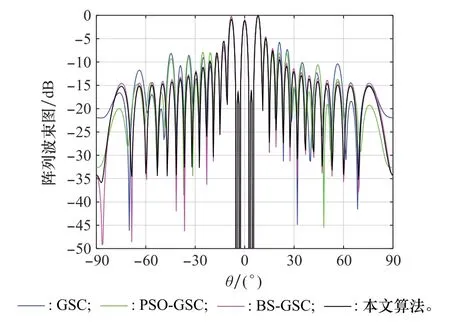
图16 来波方向为0°、3°、-5°、5°、-3°时波束方向图Fig.16 Beam pattern when the incoming wave direction is 0°,3°,-5°,5°,-3°
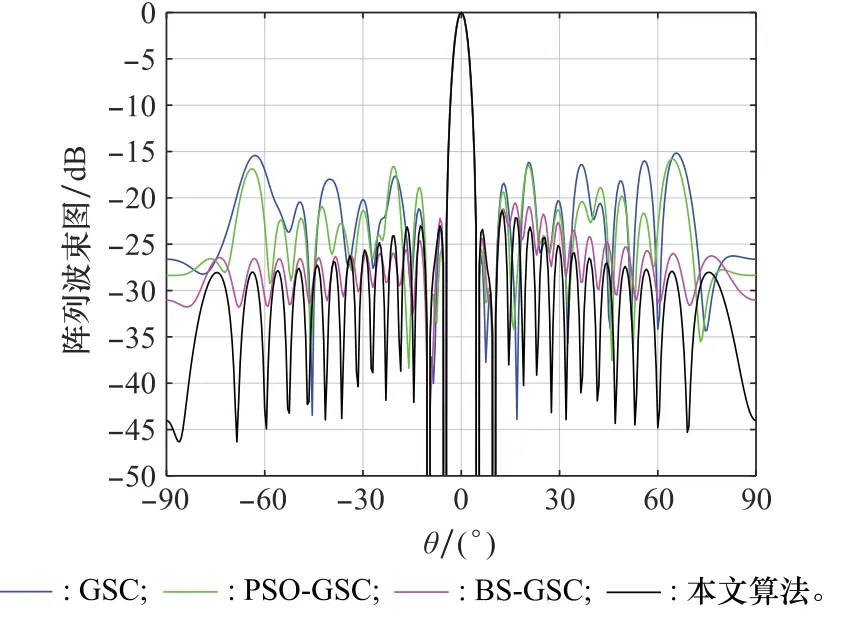
图17 来波方向为0°、5°、-5°、10°、-10°时波束方向图Fig.17 Beam pattern when the incoming wave direction is 0°,5°,-5°,10°,-10°
由图18可知,当SNR小于10 dB时,4种算法的输出SINR均随SNR增加而近似线性增加,且输出SINR的值较为相近;当SNR在[10,30]dB时,GSC和PSO-GSC算法出现饱和,其他两种算法输出SINR随SNR增加而增加;当SNR大于30 d B时,本文算法输出SINR随SNR增加而缓慢增加,BS-GSC算法则出现缓慢下降的趋势。总体上看,本文算法的输出SINR相比于其他3种算法均有提高,因此在保持其他条件稳定不变的情况下,本文算法的输出形成优于其他3种算法。
3.7 输出性能分析
将快拍数设定为400,令SNR从-40 d B增加到70 dB,其他条件保持不变,比较4种算法输出信干噪比(signal to interference plus noise ratio,SINR)与输入SNR的变化关系,结果如图18所示。
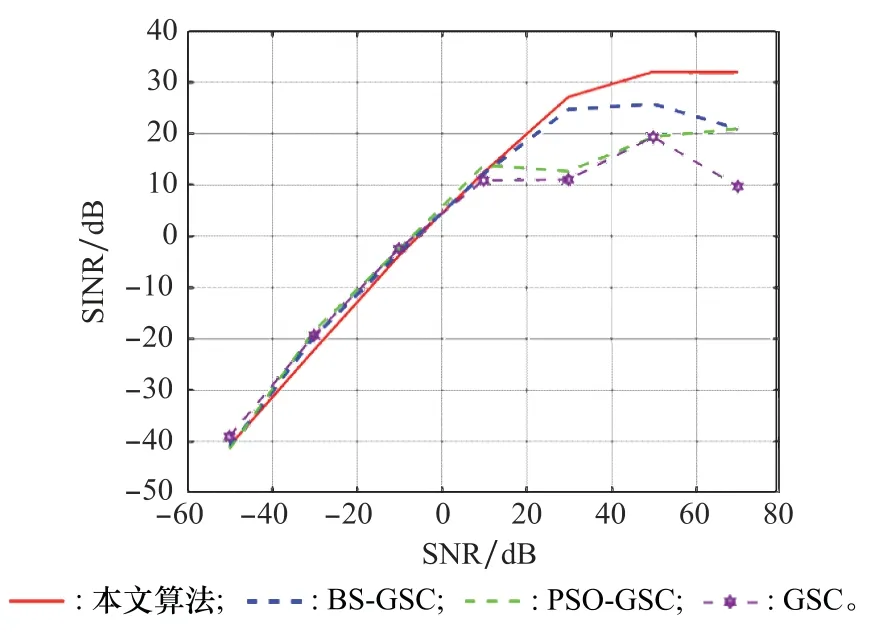
图18 4种算法输出SINR随输入SNR的变化曲线Fig.18 Variation curve of output SINR of four algorithms with input SNR
4 结 论
本文基于传统GSC算法工程应用广泛的实际,针对GSC运算量过大、波束旁瓣较高、在低快拍条件下波束形成效果不理想的问题,提出了一种基于PSO算法的BS-GSC算法。本文算法采用一种高效的自适应转换矩阵方法,将接收数据由阵元空间转到波束空间,以降低算法的自由度为前提并有效减少了运算量。同时,利用粒子群寻优手段充分挖掘信号数据的相关性,并引入压缩因子的概念增强算法的局部搜索能力,增强了算法的稳健性。仿真结果表明,本文算法在强干扰和低快拍的条件下,仍具有良好的波束形成能力,并有效改善了期望信号对消的现象。
