时间敏感网络中基于IEEE 802.1Qch 标准的优化调度机制
2022-10-09聂宏蕊李绍胜刘勇
聂宏蕊,李绍胜,刘勇
(1.北京邮电大学信息与通信工程学院,北京 100876;2.北京邮电大学人工智能学院,北京 100876)
0 引言
在许多分布式硬实时和安全关键应用领域,例如汽车和工业控制应用,当前专有的基于总线的网络技术在支持不断增长的通信带宽需求方面已达到极限[1]。以太网因支持更高的数据速率、更低的成本,在可扩展性和兼容性等方面具有很大的优势,正在开始逐步取代专有现场总线[2]。然而,传统的IP 服务允许传送数据包而不会丢失,也不会出现排序问题。但是,它们不能提供严格的QoS 保证,不适合具有高实时性与高安全性要求的应用。确定性转发服务对数据包传输过程中的时延、丢包和抖动有严格的要求,这对于严格的实时应用是非常理想的。为了实现确定性低时延传输,工业界在标准以太网的基础上提出了多种专属网络协议,如时间触发以太网(TTEthernet,time triggered Ethernet)技术、工业以太网控制自动化技术(EtherCAT,Ethernetcontrol automation technology)和串行实时通信系统(SERCOS,serial real time communication system)——SERCOSIII 等。但是,不同体系下的网络技术出现了不兼容、难移植、互操作性差等问题。在日益增长的确定性网络标准化需求的驱动下,IEEE 时间敏感网络(TSN,time-sensitive networking)工作组正在研究关键机制的标准化,提出了一系列链路层增强机制的标准和规范。
已发布的标准 IEEE 802.1Qbv[3]和 IEEE 802.1Qch[4]用于解决标准以太网中不确定性排队时延的问题。基于IEEE 802.1Qbv 的时间感知整形器(TAS,time-aware shaper)能够实现微秒级逐跳逐包的细粒度调度,TAS 需要为交换机中每个队列附加的门控列表(GCL,gate control list)进行配置。但是调度算法的运算复杂度很高,网络的任何变化都会导致GCL 重新计算和配置。为了简化TSN 交换机的设计,IEEE 802.1 Qch 标准基于TAS 提出了一种名为循环排队和转发(CQF,cyclic queuing and forwarding)的易用模型,也称蠕动整形器。CQF 提供确定性且易于计算时延的时间敏感流量调度,不需要复杂的配置,TSN 的实现与管理复杂度大大降低,因此,CQF 已经成为TSN 中高选择的整形器[5]。
要充分挖掘TSN 的确定性传输能力,流量调度在保证实时传输、确定性传输中起着重要的作用,确定每个数据帧在交换机出端口的传输时隙,保证所有数据帧无冲突共网传输。研究人员对此进行了大量研究探索,目前,CQF 的工作通过启发式的轻量级简单规划,将队列长度和硬件调度时隙作为资源常数值参与调度规划的计算[6-7]。对于队列与时隙的贪心式占用方法,流量容易在队列的同一接收时隙汇集,出现队列负载不均的问题。
基于上述问题,本文设计了一种基于混合整数线性规划优化的路由与调度模型。首先,提出了基于网络与流量多属性特征的硬件时隙自适应(AHTS,adaptive hardware time slot)生成调度算法;然后,将计算出的队列长度和硬件调度时隙作为混合整数线性规划与逐流调度的流量注入时隙规划(MILP_FITP,mixed integer linear programming flow injection time planning)算法的输入来求解调度方案,MILP_FITP 算法应具有以下特性。
1) 有界时延。算法满足有界队列长度约束,并在要求的期限内将时间敏感流传输到目的地。
2) 高可调度性。算法具有高网络可调度性,在时间敏感网络中可调度数千个时间敏感流,并且保持较高的网络调度成功率。
3) 调度顺序独立。算法不完全依赖于待调度流量的先后顺序,在全局范围内完成规划与映射。
4) 端口队列长度自适应性。队列长度在满足传输需求的同时应相对较小,降低实现难度与硬件成本,在减小调度粒度的同时考虑运算时间。
5) 可行的执行时间。算法针对离线阶段最大化成功映射到目标网络上的时间敏感流的数量,均衡每个时隙所承载流量负载以提高调度方案的扩展能力,因此要求运算时间低于动态规划阶段的调度规划算法。解决方案应该具有可接受的算法执行时间和高质量求解结果。
本文主要的研究工作如下。
1) 基于软件定义网络架构和循环队列与转发机制,在TSN 中开展数据流的全局路径规划、队列规划与时隙分配的联合调度,实现局域网中流量的自动化控制与调度。
2) 提出了网络与流量多属性特征的硬件调度时隙自适应生成算法,实现队列长度与硬件调度时隙的自适应配置,以实现调度粒度与运算时间的平衡,提高网络的调度能力。
3) 提出了MILP_FITP 算法分别对端到端截止时间要求高的流量进行逐流调度,对多偏移量可选择的流量的混合整数规划模型进行规模缩减以加快求解速度,通过均衡资源利用进一步提升网络的可调度性。
4) 仿真结果表明,所提算法具有很好的网络调度和资源利用率性能,具有可行的执行时间。与按流顺序逐时隙调度(FJ-FO,flow injection by flow order)方法、按流顺序随机时隙调度(FJ-random,flow injection by random)方法、基于特定领域知识的禁忌搜索启发式(Tabu-ITP-change,Tabu-injection time planning in exchanging mode)算法和基于一次性分配结果的偏移调整注入(FO-CS,flow offset and cycle shift)方法对比,验证了所提算法的有效性。
1 研究背景与相关工作
1.1 CQF 调度机制
循环排队与转发传输示意如图1(a)所示。CQF 将一个输出端口的发送时间分为一系列相等的时间间隔,每个时间间隔被称为一个周期,持续时间为Lslot。循环排队与转发队列示意如图1(b)所示。CQF 通过利用2 个交替执行入队和退队操作的队列,保证奇队列中的一个数据包在奇周期循环内从上游节点发送,并在同一周期内被下游节点接收并缓存到偶队列中,偶周期循环中情况则相反。因此,端到端的时延只取决于循环长度和路径跳数H,最大时延约束为(H+1)Lslot,最小时延约束为(H-1)Lslot,有2Lslot的抖动,提供了确定性的排队和转发。同时,其他类型的流转发与时隙无关,图1(a)中浅灰色长方形表示尽为而为(BE,best effort)流,它们可以在未被完全规划的时隙内进行节点之间的传输以提高带宽利用率;ES 表示网络中的端系统;SW 表示TSN 交换机;τ表示一个硬件调度时隙。图1(b)中Q 表示优先级队列。
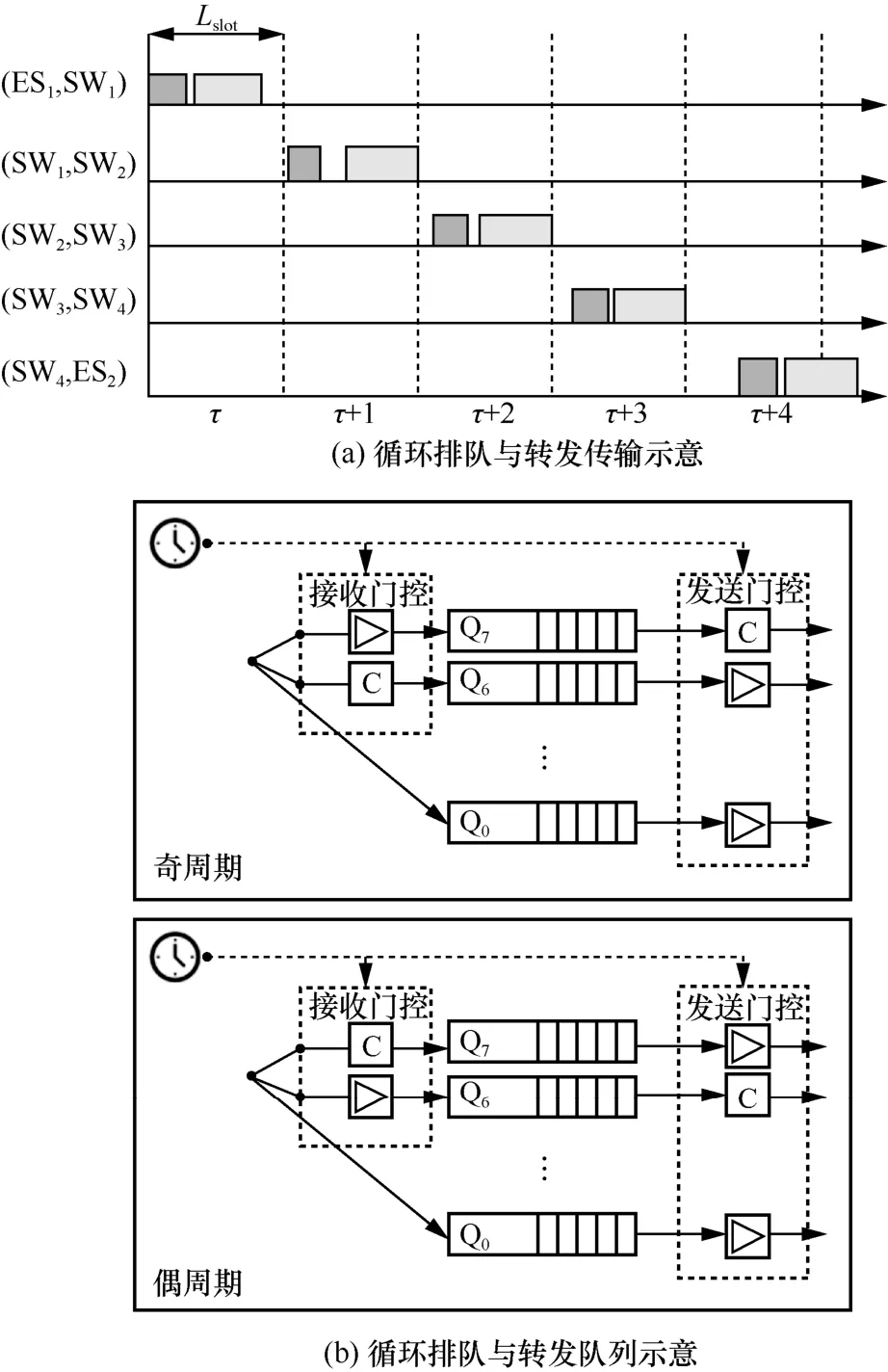
图1 循环排队与转发机制示意
1.2 相关工作
流调度计算本身是一个复杂的问题,它已经被证明是一个NP-hard 问题。TSN 中基于IEEE 802.1 Qbv 的TAS 模型对应的调度算法通常从2 个方面进行无冲突规划:空间隔离与时间隔离。空间隔离主要体现在路由算法,即为每条流选择一条传输路径。时间隔离主要体现在调度方法,即控制数据帧在何时发送出去。路由子问题的优化目标传统上基于最短路径算法,理论上单一流可以实现从源到目的端的最快调度,然而,Laursen 等[8]已证明SP 算法对于TSN 来说并不是最佳路由算法,因为大量流量可能会因使用相同或部分相同路径而出现调度瓶颈,导致网络不可调度。基于不同优化目标的启发式算法被提出,例如,文献[9]提出了基于遗传算法的启发式路由与算法,主要目标是满足流的最后截止期限,该算法结合了路由和调度约束,使用联合约束生成静态全局调度;文献[10]引入了启发式列表调度器,在一个步骤中使用联合路由和调度约束生成有效的调度以实现整个网络的负载平衡;文献[11]提出了一种混合遗传算法的设计方法,包括TSN 中路由和调度问题的染色体表示、遗传算子的选择以及邻域搜索,以找到接近最优的网络负载平衡的解决方案;文献[12]基于启发式K最短路径启发式方法与基于贪婪随机自适应搜索过程的元启发式算法来解决时间触发的联合路由和调度问题,最小化使用队列的数量以及流的端到端时延。
可满足性模理论(SMT,satisfiability modulo theories)[13-15]和整数线性规划(ILP,integer linear programming)[16-19]数学理论可以用来解决路由和调度问题,通过建立网络与流量的关键约束求解满足要求的路由规划与调度方案。文献[20]使用一阶逻辑约束来定义调度问题,分别调用SMT 和MIP 求解器,在有和没有优化目标的情况下求解方案。文献[21]提出了分组调度机制,建立路由和调度的整数线性规划模型,通过拓扑修剪和基于谱聚类的流分组策略缩小约束的规模,在较短时间内进行模型的求解,保证一定的调度成功率。文献[22]提出冲突程度感知流分区多路径路由技术和基于迭代整数线性规划的可伸缩性调度技术提高调度成功率和容错性。文献[23]建立了一种新的无冲突网络更新的ILP 调度模型,保证了网络更新中没有帧损失,也没有引入额外的更新时间。
ITP(injection time planning)算法[6]通过将循环流的注入时间映射到队列资源来实现CQF,简化了GCL 的配置,通过随机交换调度成功的流量集合与调度失败的流量集合以提高调度成功率,得到近似优化解,但未考虑不同场景下队列长度与硬件调度时隙对调度性能的影响。文献[7]在ITP 的约束模型下提出了在线流注入时间调度算法,根据网络资源利用率调整网络适配器上的发送时间,为新的时间敏感流增量生成流量调度,不需要重新配置先前规划,实现了快速调度。
综上所述,现有的优化算法分别采用启发式算法、元启发式算法以及整数规划求解算法求解近似最优调度规划,求解速度依次递减,求解质量依次递增。现有的CQF 调度机制采用逐流调度方式和启发式算法为网络实现一个可用的规划,网络调度成功率有待提高,且算法的优化解与最优解未进行对比。为此,本文针对局域网络中的时间敏感流量大规模调度问题,提出了基于CQF 整形机制的联合路由与调度优化的全局规划加速生成算法,保证流量的有界时延、网络高可调度性、调度独立性与可接受的执行时间。
2 数学模型
TSN 架构如图2 所示。支持CQF 整形机制的TSN 架构基于IEEE 802.1Qcc[24]所提出的全集中式控制架构的控制配置模型,通过一个中心化用户配置节点与终端用户之间交换用户需求。用户网络接口(UNI,user network interface)位于中心化用户配置(CUC,centralized user configuration)与中心化网络配置(CNC,centralized network configuration)之间。CUC 收集数据平面中网络拓扑、流特征以及用户需求,并将用户需求传达给CNC,控制面从全局资源视角将网络资源与流特征作为调度算法的输入,计算出满足传输要求的配置并下发给各个设备。随后,数据平面设备根据收到的配置来自动控制数据包的发送、缓存与转发。
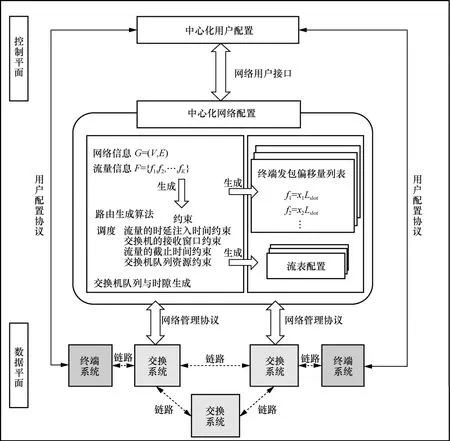
图2 TSN 架构
TSN 被建模为有向图G=(V,E),其中,V=ES ∪SW 是网络中所有节点的集合;E⊆V×V表示2 个节点之间有一条全双工链路,每一条全双工链路都可以被2 个方向的逻辑链路表示为(vi,vj)和(v j,vi),其中前面的元素表示源端系统,后面的元素表示目标端系统;分别表示网络中节点数和链路数。支持CQF 机制的TSN 交换机结构如图3 所示。交换机支持U个输入/输出端口,每个端口支持8 个输出队列。IEEE 802.1Q[25]标准封装了虚拟局域网数据帧格式,以太网报头中的优先权代码点(PCP,priority code point)字段标记了数据流的优先级。两队列用于时间敏感流的排队转发,在奇偶周期交替打开队列6 和队列7。

图3 支持CQF 机制的TSN 交换机结构
时间关键型应用被建模为周期性流量,每个流量都在其周期内传输。考虑一组K个周期性单播时间敏感流集合F={f 1,f2,…,fk,…,fK},为了简化,多播的情况可以被分割成具有相同源和不同目的地的多个单播流。每个流由源端系统、目标端系统、帧长度、流量周期、允许的最大端到端时延、有序的传输路径和流量注入网络时隙的七元组来定义,即
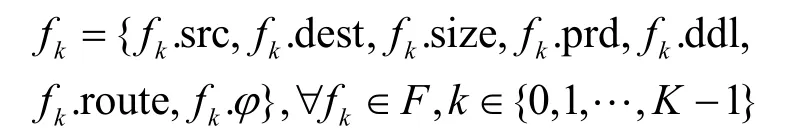
其中,f k.route 和f k.φ分别由路由算法和调度算法生成后配置。系统参数如表1 所示。

表1 系统参数
3 问题描述
在本文中,对于给定网络拓扑和流量集合,求解的流路由与调度方案需要满足以下约束。
1) 路由约束
如果节点vi是流fk的源节点,则

如果节点vi是流fk的目的节点,则

如果节点vi是流fk流经路径的中间节点,则

为了防止出现循环路由同一个节点的情况,对于流fk的每条预留链路最多仅可访问一次,即
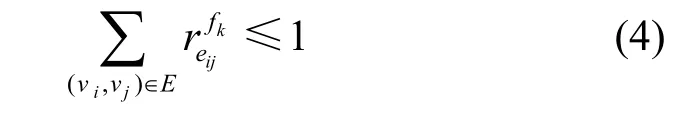
2) 调度约束
与调度问题相关的CQF 队列长度、硬件调度时隙和交换机出端口的调度周期分别表示为Lqueue、Lslot和Tschedule。对于不同时间生成的流量,通过注入网络时间的规划实现对TSN 的高效调度。
①流量的时延注入时间约束
假设所有的流都在零参考时间开始计算流的偏移量,为了使流量可以按门控列表周期性地进行有序传输,需要保证时间敏感流在它本身的周期内发送出去,不会与流量下个周期的数据帧发生冲突,即

② 交换机的接收窗口约束
该约束是用来检查数据包是否在窗口右端内到达,理论上如果硬件调度时隙满足最小时隙约束,则所有数据包都会满足该约束。对于任意时间敏感流fk在每一跳的接收时隙为

③流量的截止时间约束
为了保障时间敏感流的有界低时延传输,流的所有数据包要在指定时间之前到达目标端系统,即

④ 交换机队列资源约束
TSN 交换机中队列的缓存容量有限,在每个时隙中队列缓存的数据包总大小不能超过缓存大小,数据流fk在链路上所占用的时隙可表示为

对于某个端口的任意时隙,端口传输的流的总大小不应超过队列缓存大小,否则队列溢出,即

3) 硬件调度时隙约束硬件的调度粒度为一个时隙,所有流量周期都应被预定义的Lslot整除。最大时隙约束是所有流量周期的最大公约数(GCD,greatest common divisor),根据流量周期特征获得的时隙上界为

CQF 标准规定数据包在相邻2 个节点的发送时隙和接收时隙相同,则最小时隙需要保证队列中的所有数据包在相同的时隙内从上游节点传输到下游节点,时隙的下界约束为
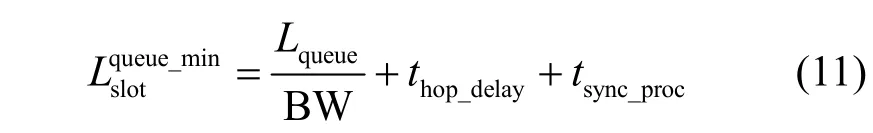
其中,BW 为链路的发送速率;thop_delay为交换机的每跳固定时延,包括处理时延和传播时延;tsync_proc为时钟的同步精度。
考虑数据流最大容忍时延需求和网络特点,基于流量完全调度的要求,截止时间要求最高的流量有规定时间内送达的约束对硬件调度时隙有上界要求,表示为
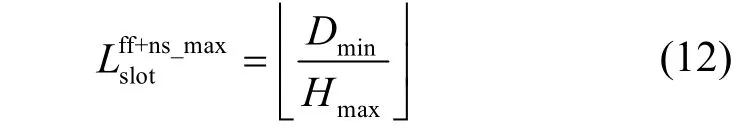
其中,Hmax表示深度优先搜索方法得到网络的最长路径,Dmin表示流量集中流量DDL 的最小值。如果小于时隙的下界值,则认为该流量无法在网络中调度;否则作为硬件调度时隙上界约束。
4 算法提出
在标准以太网交换机中,数据包存储在缓冲池中,而队列用于存储数据包的元数据以进行调度。因此,交换机中的最大队列长度等于缓冲池中数据包缓冲区的数量。端系统为避免占用过多的缓存空间会在数据产生后立即发送,如果没有严格且详细的发送时间规划,流量很容易集中到队列的部分时隙中转发。由于队列长度是有限的,一旦数据量超过缓存大小,会出现队列溢出,导致数据包被丢弃。实际上,可以通过时延流的发送时隙来缓解此问题,从而使队列的时隙利用更加平衡。但是当流注入网络的偏移量过大时,终端需要缓存大量的数据包,耗费大量的存储空间,这将限制终端的发包数量和种类。根据以上分析,在设计调度算法时主要需要解决以下2 个问题。
1) 基于流特征、网络规模和流量规模确定硬件时隙长度和缓存队列长度
从调度模型分析,Lslot与流的周期属性、截止时间属性、链路速率、交换机缓存队列长度、网络规模等因素相关,交换机缓存队列长度的增加在一定程度上会增加Lslot的下界值。文献[6-7]表明,Lqueue增加会使所容纳的数据包会增加,可调度的流数也增加。然而,上一时隙缓存的数据包必须在下一时隙全部发送这一约束将增加数据流的单跳时延,经过路径累积会增加数据流的端到端总时延,导致流量不可调度。受到底层硬件资源的限制,Lqueue增加会使交换机的内存需求增大,交换机的实现难度和成本也会增加。更重要的是,门控的控制精度与Lslot成反比,在给定流量周期的情况下,源端系统可选择的注入偏移随Lslot减少会增加,在提升控制精度的同时会增加搜索空间。Lslot的大小受到链路带宽的约束,如果预留的时间远超过队列缓存所需要的发送时间,剩余时隙将会出现无数据传输的情况。因此,硬件调度时隙Lslot对基于CQF 机制的网络传输性能产生重要的影响。


在算法1 中,基于硬件调度时隙约束计算得到Lslot的上下界,当给定的Lqueue过大时,生成的硬件调度时隙下界值过大,Lslot不能整除所有数据流的周期,则不能保证流量集合F的调度(1)~2)行)。算法以MTU 的幅度进行调节,以保证数据传输的可调度性与完整性(3)~5)行)。检查在交换机缓存队列长度最低门限下的硬件调度时隙范围是否满足流量的截止时间属性,将可能不可调度的流移入集合Fddl(6)~12)行)。如果调整后的CQF 缓存队列长度大于最低阈值,则利用优化器对硬件调度时隙进行整数规划优化(13)~22)行)。为了平衡调度控制粒度和调度时间敏感流的数量,在模型中引入时间敏感流的带宽利用比例阈值β,剩余部分可供给其他类型流量利用,也可以作为提供因同步时间精度不够所溢出的数据帧的余量时隙长度以供动态调整。最后利用优化的硬件调度时隙筛选出可能不可调度的流移入集合Fddl,更新待调度流量集合F*(23)~24)行)。
2) 进行合理的时间敏感流路由与注入时间映射
基于路由约束式(1)~式(4)和调度约束式(5)~式(9),构建联合路由和调度问题为混合整数线性规划,考虑均衡分配流量占用的路径与时隙,以最大化可调度流量数量,最小化繁忙链路队列利用率为目标,获得最优的流量路由与时隙偏移分配策略。CQF-TSN 调度问题可以表述为以下MILP 问题。

CQF-TSN 问题搜索空间的指数增加主要来自以下两方面:每个流量可用路径的数量和注入网络偏移量的数量。除了从底层拓扑模型上可以缩减模型、减少变量与约束的数量,还可以优化ILP 生成过程本身,通过减少ILP 产生的不必要的辅助变量,减少MILP 端变量的数量以及变量的边界范围,从而减少搜索空间以降低MILP 的复杂度。
路由问题可以拆分为2 个子问题:路由生成和路由选择。对每个流fk生成一组可用路由集合,然后引入决策变量做出一个上层决策,如果流fk通过路径pk从源节点到达目的节点,则否则
对于任意流fk给定的一组路径按照流量截止时间要求升序排序,将前的流量选择最短的路径。定义路径pk的负载加权和为

流量注入网络偏移量的可选数量由流量周期与硬件调度时隙相关,搜索空间为,其中,K表示待调度流的数目。算法1 基于流量特征及网络规模将流量分为待调度的流量集合*F与可能不可调度流量集合Fddl,*F作为混合整数规划的输入,Fddl将采用增量式逐流调度选择路径链路最繁忙时隙的带宽占用率低的时隙注入网络。定义链路e最繁忙时隙的带宽占用率为

为了进一步缩减偏移量的搜索规模,待调度的流量集合F*按截止时间要求升序排序,流集合可偏移范围小于后半部分由于截止时间大的流量可调整范围较大,这部分流量应尽可能利用较大偏移量时隙对应的缓存,将小偏移量的时隙缓存留给集合中的流量,因此在约束条件中,从流量随机选取50%的流量提高偏移量选择下限为



在算法2 中,首先将待调度的流量集合F*时间要求升序排序,然后基于DDL 顺序完成路由生成与选择(1)~6)行)。基于硬件调度时隙和路由结果设置变量、更新变量空间、设置目标函数、设置约束条件和完成优化调度(7)~20)行)。完成计算密集型的精确优化之后,如果得到优化解,依次对Fddl中的流量进行调度(21)~37)行),对于注入偏移时隙调整范围内的任意时隙off,checkConstr(off)需要保证其截止时间约束满足式(7),checkSlot(off)同时保证在流量注入后该流路径上的所有出端口对应的缓存队列不存在溢出问题,满足交换机队列资源约束式(9)。off_option 包含所有满足条件的注入偏移时隙选择。为了均衡每个时隙所承载流量负载,基于式(15)为路径所包含的链路e计算最繁忙时隙的带宽占用率,并选择资源利用率最小的注入偏移时隙。如果未得到优化解,则模型设置的计算时间太小或模型不可调度。
5 仿真实验和结果分析
仿真在Python 的框架下完成,使用networkx 对网络建模并生成不同的流量集。所有的MILP 实例都在Gurobi 优化器(9.5.1 版)中求解,求解器超时时间设置为1 200 s。硬件配置为i7-8750H CPU,运行频率为2.20 GHz,内存为8 GB。为验证MILP_FITP算法的性能,将其与FJ-FO 算法、FJ-random 算法,Tabu-ITP-change 算法[6]和FO-CS 算法[26]进行了对比,禁忌表长度为500,交换概率为0.7。所对比的调度算法均基于最短路径算法计算得到的路由结果。
5.1 参数设置
设置链路带宽为1 Gbit/s,网络最大传输单位MTU=1 500 B。网络拓扑如图4 所示,这些拓扑几乎可以被组装到所有的工业网络结构中。

图4 网络拓扑
流量周期和截止时间的单位为μs,截止时间包含2 种模型,即和与网络规模、硬件调度时隙无关的模型其中,η为时延系数,无特殊说明则η=0.4。流的源端系统和目标端系统从网络中的端系统中任意生成一对,队列缓存最低门限设置为3MTU,带宽利用比例阈值β=0.9。所对比的调度算法基于固定的队列长度和硬件调度时隙,实验参数如表2 所示。

表2 实验参数
5.2 评估指标
评估算法性能由以下几个指标完成。
1) 映射流数量,给定仿真网络中的流参数,满足所有约束成功调度流的数量。
2) 网络调度成功率,表示满足所有约束的求解方案的实验次数与总实验次数的比值。
3) 已用链路平均队列时隙资源利用率(RU_U),表示实际分配流量的队列时隙资源占已用队列时隙资源的比例。
4) 可用链路平均队列时隙资源利用率(RU_A),表示理论上分配给流量的队列时隙资源占所有可用端口(不包括连接到主机的端口)队列的比例。
5) 运行时间,表示算法完成所有流量调度所需要的时间,单位为s。
5.3 仿真结果分析
1) 注入时隙方法
在MILP_FITP 算法中,优化目标是均衡时隙带宽占有率以缓解调度瓶颈,提高流量调度成功率。为验证算法的有效性,本文与4 种算法进行对比,网络拓扑为线性拓扑,发包周期从中随机选取,为了排除队列长度和硬件调度时隙的影响,MILP_FITP 算法采用表2 所示的固定配置。对比不同流量注入方案对成功映射流量数量和平均时隙带宽占有率的影响,仿真结果如图5 所示。
在固定配置下,MILP_FITP 算法精确求解后网络调度成功率达100%时最多调度2 000 条流量,因此图5(a)中MILP_FITP 算法仅保留了250~2 000 条流量的仿真结果,随着待调度流量数量增加,MILP_FITP 算法对比其他算法的改进增大,待调度流量数量为2 000 时对比FJ-FO 算法达到28%。

图5 不同注入方案对算法的影响
在相同队列与硬件调度时隙配置下,图5(b)对比了不同算法的资源利用情况,仿真网络中存在2 000 条流量,RU_A 与RU_U 越接近代表队列时隙资源的实际占用越平均。由于逐流顺序调度算法(FJ-FO 和FO-CS)映射流数量较少,理论上的资源利用率会比其他3 种算法低。FJ-random 算法随机搜索未考虑带宽利用率,虽然映射流数量有所增加,但是资源利用率与实际占用的资源利用率差值与FJ-FO 和FO-CS 相似。由于一些时隙在约束内可以使用,比如连接到端系统的交换机的第零时隙,但实际上没有数据包待转发,因此RU_A<RU_U。Tabu-ITP-change 算法基于流密度对流进行交换优化,一定程度上均衡了资源利用,但是启发类算法为了平衡求解质量与收敛速度,优化程度低于MILP_FITP 算法。
时间成本与算法关系如图5(c)所示,FO-CS 与FJ-FO 算法的解质量相近,FJ-FO 解质量相较更优但时间成本高于FO-CS。FJ-random 算法解质量适中,时间成本最低,但未考虑资源利用问题,部分时隙资源满载后调度无法调度。Tabu-ITP-change 算法在低负载下很小的迭代后收敛得到较优解,时间成本低,但是随着流量增加,计算密集型的启发式算法的求解时间很高。
2) 流调度顺序
考虑流周期、流的截止时间、数据包长度,将待调度流集合按单个因素排序后调用调度算法。网络拓扑为环形拓扑,仿真网络中存在2 000 条时间敏感流,流的截止时间采用 2 种模型,发包周期从中随机抽取。为了排除队列长度和硬件调度时隙的影响,MILP_FITP 算法采用表2 所示的固定配置,对比不同流排序方案对流映射数量的影响,仿真结果如图6 所示,横坐标表示排序原则,分别为不排序(no sort)、按流周期升序排序(f.prd)、按截止时间升序排序(f.ddl)、按包长升序排序(f.size)。

图6 不同流排序方案对流映射数量的影响
在所有排序策略中,MILP_FITP 算法均优于其他算法,和流的调度顺序无关,实验结果和预期相符。在流截止时间升序排序之后f.ddl 小的流先调度,避免了在无序情况下队列与时延约束而导致的不可调度,该排序方式获得最优性能。由于截止时间模型ddl(1)极大减少了因超时而导致的不可调度,因此排序后FJ-random、Tabu-ITP-chang 算法也均可实现2 000 条流量成功调度。基于流量密度的注入时隙的Tabu-ITP-change 算法映射结果优于随机选择注入时隙的FJ-random 算法映射结果。顺序注入时隙的FJ-FO 算法在所有排序策略中映射流数量均小于其他算法。逐流调度算法理论上先调度的流可选择的资源更多。FJ-FO 算法按流顺序优先选择最近的时隙,减少了流时隙的排列数量。由于流生成周期、包长、截止时间均是随机产生的,因此未排序时调度顺序随机性更大。排序原则使流在某些特征上有序,因此算法在排序之后成功映射的流数量反而变得更少,并且受到排序策略影响的程度更大。逐流调度算法中,随机性越好映射流数量越多,且在热点链路上的流量调整会在一定程度上提高算法的性能,但是并不能让算法保证完全调度。
3) 网络拓扑对算法的影响
为了探究网络拓扑对所提算法的影响,假设仿真网络中待调度流的数量为2 000 条,分别评估线性拓扑、环形拓扑和雪花形拓扑下的映射流数和平均求解时间,仿真结果如图7 所示。
不同网络拓扑下对映射流数和时间成本比较了5 种算法,如图7(a)所示,MILP_FITP 算法和Tabu-ITP算法在不同网络拓扑下映射流数最高,FJ-random 算法次之,MILP-FITP 算法映射流数比FJ-FO 算法和FO-CS 算法这类逐流顺序调度提高了大约15%。与其他2 个拓扑相比,大多数算法的线性拓扑中的映射流数最少,原因是每个交换机在线性拓扑中最多只存在2 个方向的出端口,任意两端系统之间只存在唯一传输路径,根据队列时隙资源的占用发现,随着映射流量的增加中间4个交换机会陆续在队列资源占用上出现满载。MILP_FITP 算法通过全局资源使用的优化可以在3 种拓扑中实现2 000 条流量完全调度。

图7 不同网络拓扑对映射流数和平均求解时间的影响
如图7(b)所示,大多数算法在雪花形拓扑下运行时间最长,环形拓扑次之,线性拓扑与环形拓扑接近。原因是线性拓扑与环形拓扑在网络规模上接近,而雪花形拓扑网络规模最大,路由与调度的搜索空间要大得多。FJ-FO 算法、FJ-random 算法和FO-CS 算法平均求解时间为100 s 以下,Tabu-ITP-change 算法平均求解时间最长,MILP_FITP 算法次之。在此网络规模下,Tabu-ITP-change 算法所计算出的现有的最佳解接近最优解,由于搜索空间大且需要多次交换迭代以防止局部最优结果,时间成本要高于MILP_FITP 算法。
4) 流量特征对算法的影响
为了探究流量数据帧长度、流量周期以及流量截止时间对算法的性能影响,以Tabu-ITP-change算法作为参考进行如下性能对比。
①数据帧长度
测试的网络拓扑为雪花形网络,流量周期从{1 000,2 000}μs 中随机选取,应用2 种截止时间模型,数据帧长度为125~500 B 的小包、500~1 000 B 的中包、1 000~1 500 B 的长包以及125~1 500 B 的随机包。
不同包长对调度性能的影响如图8 所示,横坐标表示待调度流数量,折线图表示Tabu-ITP-change 算法成功调度流百分比,Tabu-ITP-change 算法无法实现完全调度,柱状图表示AHTS+MILP_FITP 算法网络调度成功率。AHTS+MILP_FITP 算法在一定范围内可以实现完全调度。AHTS 算法根据流量特征、网络规模生成队列长度和硬件调度时隙以最大化流量调度,AHTS算法确定Lqueue和Lslot后,重复100 次实验以统计网络调度成功率。在1 000 条以下轻负载的时间敏感流场景下并不会出现资源争用问题,所提算法可以完全求解。包长增加会在不同阶段出现无法调度的问题,增加队列长度虽然会缓解资源争用问题,但是Lslot增加伴随着无法满足时间敏感流的时延约束问题。一旦AHTS+MILP_FITP 算法出现网络调度成功率下降,说明网络在满负荷运转,增加待调度流数量无法提高成功映射流数量。从图8 中的柱状图可以看出,待调度流为600 条时长包出现网络调度成功率降低的现象,而待调度流超过800 条时中包和随机包均出现了网络调度成功率降低的现象,中包对应的网络调度成功率更高。Tabu-ITP-chang 算法在900 条流之后随机包对应曲线高于中包对应曲线柱状图现象相符。
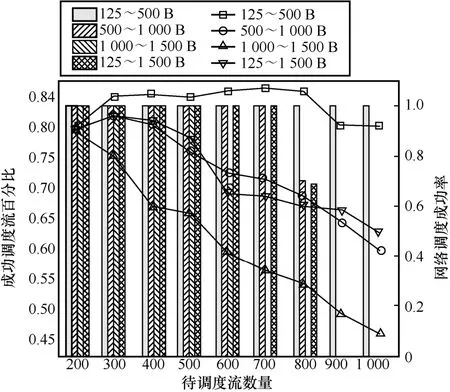
图8 不同包长对调度性能的影响
② 发包周期
网络拓扑为雪花型拓扑,流的截止时间为ddl(2),时延系数为0.9,发包周期从{1 000,2 000}μs 中随机选取。不同周期对调度性能的影响如图9 所示,横坐标为待调度流数量,实线对应左纵坐标表示Tabu-ITP-change 算法在不同发包周期下的成功调度流比例,虚线对应右纵坐标表示保证待调度流完全映射性能下MILP_FITP 算法所使用的缓存队列长度。

图9 不同周期对调度性能的影响
随着发包间隔增大,时间敏感流从端注入网络的时隙有更多选择,可调度的流数量随之增加。由图 9 可知,采用固定Lslot和Lqueue配置的Tabu-ITP-change 算法流量调度性能较低,当仿真网络里的流量增加时,成功调度流比例在不同的发包周期下均出现下降的情况。雪花形拓扑路由的最大跳数为4 跳,在时延系数为0.9 情况下,发包周期为1 000 μs 的数据会产生超时情况,而低频流的截止时间范围更大,流量不会因为时延约束而无法调度。因此发包周期为1 000 μs 对应的曲线下降更快。由于队列溢出情况的出现,增加待调度流数量即使成功映射的流数量会增加,但映射比例在下降,因为部分帧长度较小的流被替换进调度成功流集合中。在式(5)~式(9)的约束下,Lslot会限制时隙的选择,Lqueue会限制容纳流量的数量。自适应的硬件调度时隙与队列长度可以有效提升调度流比例,MILP_FITP 算法几乎保持全部映射。进一步探究在保持全部映射的性能下队列缓存长度的变化,随着待调度流的增加,发包周期大的流所需要得到的队列缓存长度会比发包周期小的流短,由于相同时间内发送的数据包会少于高频流,因此其会在较大待调度流数出现队列缓存瓶颈问题。高频流的低时延要求会导致网络中存在流数上限,不能理想地增加缓存队列长度,由于Lslot会对应增加以满足式(11),因此图9 中超过一定数量的待调度流没有标记,流数超过临界值的网络无流调度。
③截止时间
网络拓扑为雪花形拓扑,流量周期从{1 000,2 000}μs 中随机选取,应用2 种截止时间模型,使用的时延系数分别为0.4 和0.9。仿真结果如图10 所示,横坐标表示待调度流量数量。

图10 不同截止时间对调度性能的影响
如图10(a)所示,实线对应Tabu-ITP-change 算法性能,纵坐标表示成功调度流百分比。由流周期和时延系数决定的截止时间模型,其时延系数越大,可选的注入时隙越多,映射比例越大。影响算法调度性能的主要原因如下:1)Lslot不合适,无论如何优化流量的注入时间也无法在规定时间内到达终端系统;2)Lqueue不合适,在某些节点的队列出现溢出现象。截止时间模型ddl(1)中,在500 条流量以内,Tabu-ITP-change 算法在固定配置下基本上实现完全映射,有一小部分流量因为搜索不完全的原因导致时延约束无法满足。由于Lqueue不合适导致网络无法承载更多的流量,待调度流大于700 条时调度性能明显下降。虚线对应AHTS+MILP_FITP 算法的调度性能,提出算法在一定范围内可以保证待调度流的完全调度。图10(b)给出了不同截止时间下队列长度与硬件调度时隙的选择情况,左纵坐标表示CQF队列长度,右纵坐标表示硬件调度时隙。不同截止时间下的时隙长度曲线重合,队列长度柱状图持平,表明在可调度流量数量范围内,流的截止时间模型与容忍性并不影响队列缓存长度和时隙长度的选择,网络中待调度流数不同时,其优化计算得到的队列长度和时隙长度可能是相同的。当流截止时间要求高时,只能用短时隙长度进行快速转发才能实现流调度,由于Lqueue与Lslot之间具有约束关系,且队列溢出限制支持的流数量有上限,必须启用短队列交换机进行转发,该现象与图10(a)中对应的待调度流完全映射区间相一致。当时延要求与时隙长度相关、与流特征无关时,则可以通过增加队列长度和时隙长度增加网络中可调度流数量。但是从图10(b)的趋势来看,当流量负载增大时,队列长度增加很大,有必要根据成本等因素考虑通过其他途径增加承载能力。
6 结束语
本文关注局域网中的大规模流量调度问题,提出了一个通用的全局规划高优化的路由与调度机制,建立了全局资源视图,为上层算法设计者提供了资源映射问题的高层抽象;通过建立路由与调度的混合整数规划模型,提出了一种基于流分类的MILP 与逐流调度算法。该算法使TSN 的路径上所能容纳的时间敏感流数最大,并实现了网络的负载均衡,调度结果具有扩展能力,使用工业控制网络中的3 种典型拓扑对算法进行了评估。在相同队列配置下的实验结果表明,MILP_FITP 算法与FJ-FO、FJ-random、FO-CS、Tabu-ITP-change 算法相比,映射流数最高提高28%,在队列时隙资源利用上更均衡。虽然启发式算法通过引入流密度方差和多类型加权排序使映射质量获得良好的改进,但在测试规模下求解的时间复杂度与精确算法相比并不低,且求解质量低于MILP_FITP 算法。实验结果表明,在中小型局域网络中AHTS+MILP_FITP 算法显著提高了网络的调度能力,实现了可接受时间成本内路由与时隙调度规划的优化。
