基于ADAMS 的麦弗逊悬架运动学结构参数优化

柴 牧，高翎玮，欧阳东成

（1.佛山科学技术学院机电工程与自动化学院，广东佛山 528225；2.佛山市飞驰汽车科技有限公司 技术研发中心，广东 云浮 527326）

麦弗逊悬架由减振滑动立柱与横摆臂组成，具有结构简单紧凑、制造成本低、安装定位精度高及簧下质量小等优点，广泛应用于乘用车辆及部分轻型载货车辆［1］。与双横臂等独立悬架相比，麦弗逊悬架的横向刚度较小，且车轮定位参数随车轮跳动的变化量较大，通常需对横摆臂及其他杆件的硬点位置进行优化，使车轮定位参数随车轮跳动的变化处于合理范围，以满足其性能要求。

近年来，国内外学者及生产厂家在麦弗逊悬架的硬点参数优化工作中取得了较多研究成果，目前常用的方法是利用ADAMS/Car 建立悬架模型，调用Insight 模块进行悬架运动学仿真并进行多目标优化，已取得了一定的优化效果［2-5］，但这种方法缺乏自动搜索最优解的能力，往往不能获得最优结果。部分学者利用遗传算法、粒子群算法、NSGA-Ⅱ算法和NCGA 等算法对重要硬点进行优化并取得良好效果［6-9］，但由于算法接口问题导致优化结果不够直观，且优化设计过程较繁琐。文献［10］基于机械参数的不确定性问题提出并设计了DL-MOPSO 算法对硬点坐标进行优化设计，并且对比了传统MOPSO 算法和GA 算法的优化结果，结果表明DL-MOPSO 算法的优化效果更优，改善了悬架的运动学特性，但该算法的优化效率有待研究和改进。文献［11-13］利用空间机构运动学和数值计算的方法建立了麦弗逊悬架的运动学特性数学模型，并编制算法进行硬点参数的优化，减小了车轮定位参数的变化量，但建模过程较复杂且优化结果不够显著。

针对目前有关麦弗逊悬架的运动学优化效果不明显的问题，本文利用ADAMS/View 建立麦弗逊悬架系统模型，以车轮定位参数和车轮侧向滑移量为优化对象，通过经验值确定主销内倾角、主销后倾角、车轮外倾角和车轮前束角的理想变化范围作为容限，利用容限法计算各车轮定位参数的权数，以加权组合法将各车轮定位参数的子目标随车轮跳动的变化量加权以组合成优化目标函数，约束硬点变量取值范围，对硬点变量进行灵敏度分析，选取灵敏度较大的硬点，添加约束条件并采用OPTDES-SQP 算法进行迭代优化。仿真计算得到最优的硬点坐标，显著减少车轮定位参数和车轮侧向滑移量随车轮跳动的变化量，从而提高麦弗逊悬架的运动学特性以及整车的操纵稳定性。

1 悬架模型的建立

1.1 模型简化分析

悬架的运动学分析主要研究车轮跳动时导向机构对车轮的约束作用及车轮定位参数的变化关系，与整车的操纵稳定性有较大关系。合理布置麦弗逊悬架的杆件长度及安装位置能有效减少车轮定位参数的变化量，提高整车的操纵稳定性。悬架的弹性运动学分析研究了连接衬套等弹性连接元件影响下的运动学分析，但橡胶衬套的弹性力学较为复杂，如果没有精确的衬套模型，反而会降低运动学分析结果的可靠性。而传统的悬架运动学分析结果则是建立在车辆极限工况下的分析，使结果的可靠性得到了提高。因此，本文不考虑弹性运动学分析及动力学分析。由于悬架系统的零部件较多，为方便在ADAMS/View 中建模及提高仿真效率，对模型进行以下简化处理：

（1）将悬架结构简化为由横摆臂、转向节、转向横拉杆、减振器、弹簧和轮胎等主要部件构成，忽略缓冲块等影响较小的部件。

（2）减振器用质量杆件代替，阻尼用弹簧-阻尼代替，轮胎刚度用弹簧代替，悬架及转向系统零部件均为刚体，忽略部件连接间的衬套及弹性元件的影响，不考虑运动副间隙及摩擦力。

（3）建立一集中质量块代替轿车车身并固定在大地上，悬架及转向系统部件与车身相连，模拟实际的安装连接。

（4）假设左、右悬架为对称模型，建立左前1/4 悬架系统模型，测试台分别采用移动副与大地连接，并施加幅值为100 mm 的正弦驱动作为激励模拟车轮的上、下跳动。

简化后的模型如图1 所示，其中，横摆臂绕其与车身连接点A、B 相连的轴线作旋转运动，建立A、B中点作为转动副位置，横摆臂与转向节在连接点C 处采用球副连接，转向横拉杆与车身和转向节连接点D 和E 处均采用球副连接，车轮与转向节在其质心处采用固定副连接，减振器由上、下两部分组成，且上、下两部分用移动副连接，减振器下部与转向节固定，上部与车身采用球副相连，测试平台与大地之间建立移动副并添加平移驱动以模拟车轮的上、下跳动。

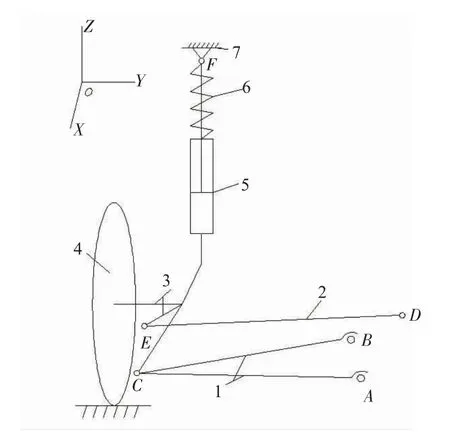
图1 左侧悬架结构示意图

1.2 模型的建立与调试

根据某轿车前悬架的硬点位置坐标和实车参数，在多体动力学软件ADAMS/View 中建立悬架系统模型，如图2 所示。研究麦弗逊悬架的运动学特性，测试主销内倾角、主销后倾角、车轮前束角、车轮外倾角和车轮侧向滑移量随车轮上、下跳动时的变化曲线，根据曲线的变化趋势和变化量的大小来判断悬架运动学特性的优劣。考虑到车轮上、下跳动时转向系统和悬架系统的相互影响，转向横拉杆与车身采用球副连接，以减少转向系统对车轮定位参数的影响。对仿真模型进行静平衡测试，获取螺旋弹簧及车轮模拟弹簧的预载荷，对比理论计算的预载荷，验证模型的合理性。模型参数如表1 所示。

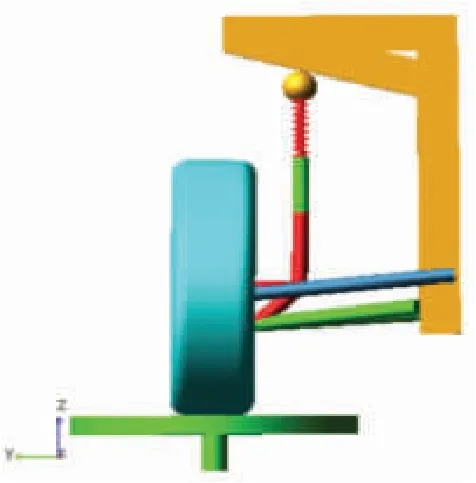
图2 悬架系统ADAMS 模型

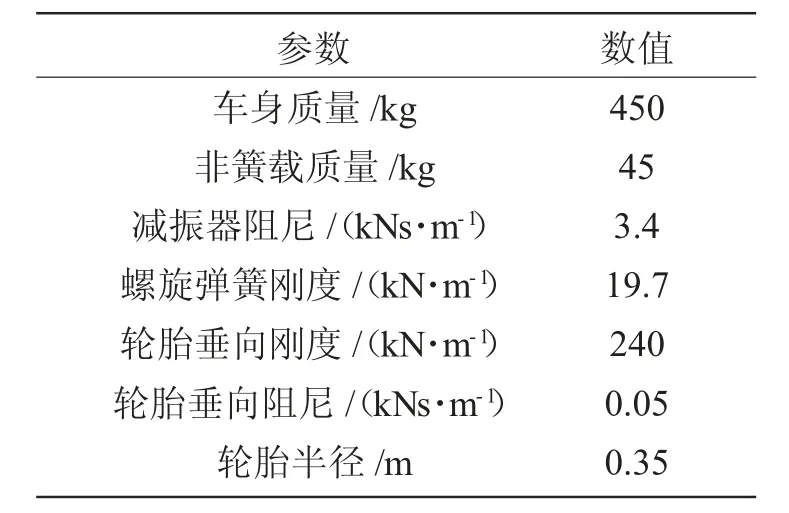
表1 模型参数

2 多目标优化仿真分析

2.1 优化目标的确定

悬架的运动学优化研究涉及到多个目标参数的优化，通常以车轮定位参数包括主销内倾角、主销后倾角、车轮前束角和车轮外倾角为主要因数的多目标优化问题。求解多目标问题的常用思路是把多目标优化问题转化为单一目标问题，主要方法有功效系数法、主要目标法、加权组合法等，其中又以加权组合法最为常用。通过选取适合的子目标函数的权重，能得到对各变量响应较好的优化目标函数，把多目标优化问题转化为单目标优化问题。

在ADAMS/View 中建模并使用其中的OPTDES-SQP 算法进行迭代优化。OPTDES-SQP 算法为二次规划算法，对具有约束范围的变量目标优化等非线性问题具有较好的优化效果，适用于悬架的运动学优化。由于该方法只能优化单一目标函数，因此需要把运动学优化的多目标问题转化成单一目标函数问题进行求解。车轮各定位参数对悬架的运动学特性影响较大，因此采用加权组合法对主销内倾角、主销后倾角、车轮前束角及车轮外倾角加权求和作为优化目标函数。

优化目标函数为各车轮定位参数与对应权数的乘积之和，故权数的确定是否合理直接影响仿真优化结果。因此，合理地选择权数对目标优化具有重要的意义。由于各车轮定位参数的变化量具有一定的合理范围，故采用容限法进行权数的确定［14］。

若已知各子目标函数fi（x）的变动范围为

则该目标函数的容限由下式确定

其中，权数wi可确定为

式（1）～（3）中，mi、ni为目标函数值的下限及上限，wi为各目标权数。采用容限法确定权数时，当子目标函数变化范围较大时，作用影响较小；相反，如果子目标函数变化范围较小，则影响作用较大。如本次优化的车轮前束角，合理范围为-0.75°～0.75°，合理变化范围相对较小，因此前束角变化量的权数比较大，以加强前束角变化量对优化目标函数的影响，达到平衡各子目标数量级的作用。参考汽车工程手册及其他文献的车轮定位参数经验范围确定优化子目标容限的变化范围［1，15］，计算得到各目标权数，如下表2所示。

表2 车轮定位参数权数

悬架运动学优化的目的是使各车轮定位参数随车轮上、下跳动时处于经验范围并且变化范围尽可能小，加权后得到如下优化目标函数

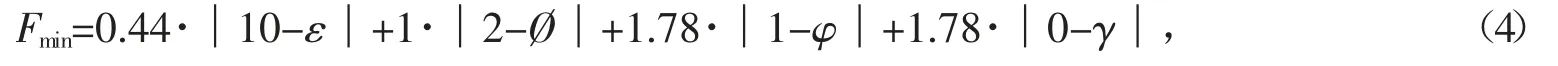
其中，ε，Ø，φ，γ 分别代表车轮上下跳动时的主销内倾角、主销后倾角、车轮外倾角、车轮前束角。

2.2 优化仿真分析

根据经验，麦弗逊悬架中对车轮定位参数影响较大的重要硬点主要有横摆臂与车架铰接点、转向横拉杆内外点和主销连接点。分别将以上硬点坐标的x、y、z 作为设计变量，变量约束按限制干涉条件确定，同时需要满足设计导向机构的性能要求，如横摆臂和车架的后铰接点应高于前铰接点以提升整车制动时车身的抗前俯特性，静态时横摆臂外点不低于内点以保证侧倾中心高度处于合理范围等。设计变量优化范围均设置为±20 mm，对测试台施加幅值为100 mm 的激励模拟车轮上下跳动，对各设计变量进行灵敏度测试，得到各设计变量的灵敏度如下表3 所示。

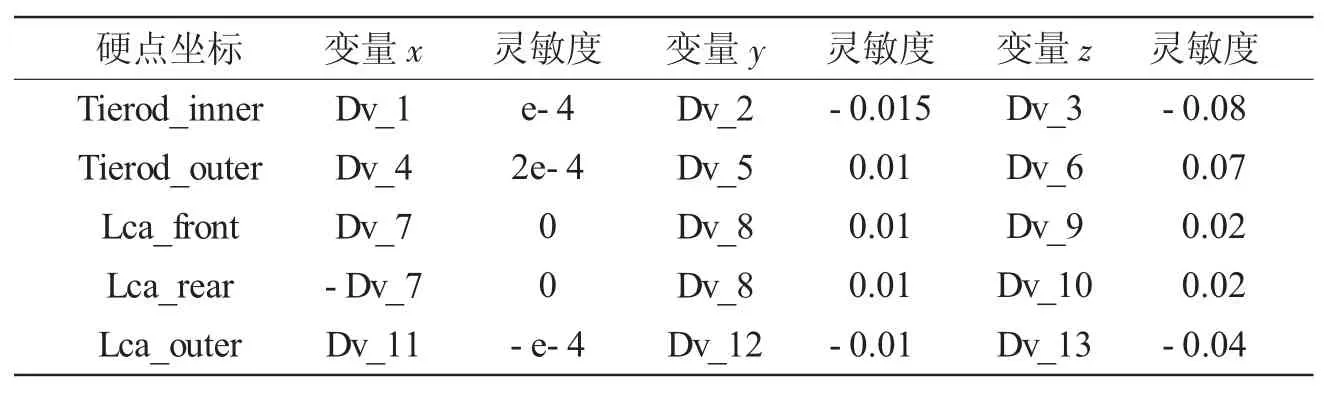
表3 各硬点变量灵敏度

比较表3 中设计变量的灵敏度大小可以得到，对目标函数影响较大（下划线表示）的设计变量为Dv_2、Dv_3、Dv_5、Dv_6、Dv_8、Dv_9、Dv_10、Dv_12、Dv_13，选取灵敏度较大的变量进行优化能够减少仿真迭代次数，增加优化结果收敛的成功率，有效提高优化效率和质量。选取上述设计变量作为优化设计变量，以横摆臂和车架铰接点满足前低后高提高整车制动时的抗俯仰特性，及静态时横摆臂外点低于内点以保证侧倾中心高度处于合理范围作为约束条件。采用OPTDES-SQP 算法进行迭代优化。

主销内倾角为主销轴线与地面垂直线在汽车横向平面内的夹角，由于汽车本身重力的作用，主销内倾能够使转向轮获得良好的自动回正能力，为汽车低速行驶时主要的回正力矩来源。如图3a 所示，优化后主销内倾角的变化范围为7.76°～10.96°，变化量为3.2°，满足设计要求，比优化前减少了19.6%，能为轿车提供良好的操纵轻便性和稳定的回正力矩，且主销内倾角随车轮上跳时增加，在车轮受到冲击发生偏转时主销内倾提供的回正力矩增大，提升了整车的直线行驶稳定性。

主销后倾角为主销轴线与地面垂直线在汽车纵向平面内的夹角，主销后倾角越大，主销后倾拖距越大，车轮的自动回正能力越强，汽车行驶稳定性越高，但过大的主销后倾角造成转向沉重，合适的主销后倾角能使转向轮获得良好的自动回正能力，为汽车高速行驶时车轮的主要回正力矩来源。优化前后主销后倾角变化较小，如图3b 所示，变化量为0.57°，处于合理范围并能够提供稳定的回正力矩，提高整车高速行驶的稳定性，且主销后倾角随车轮上跳时增加，提供的回正力矩随车轮上跳增加，符合理想的变化趋势。

车轮外倾角为车轮中心线与地面垂直线在汽车横向平面内的夹角，外倾角可以弥补汽车载荷引起的内倾，同时与主销内倾角匹配能够使汽车获得良好的转向轻便性。优化前后外倾角如图3c 所示，优化后外倾角变化范围为-0.02°～1.03°，变化量为1.05°，比优化前减少34%，从而减少了车轮跳动时轮胎的磨损，提高了轮胎的使用寿命，变化量较少的外倾角弥补了汽车载荷引起的内倾，提高了汽车直线行驶稳定性及稳态响应特性。

车轮前束角为车轮平面与汽车前进方向的夹角，车轮跳动时前束角的变化量对汽车直行稳定性和稳态响应特性有很大影响，因此设计中保持前束角不变十分重要。如图3d 所示，优化后前束角变化极小，变化范围为-0.07°～0.02°，比优化前减少了91.1%，且车轮向上跳动时前束角呈现负前束变化，使汽车呈现不足转向特性，优化后汽车直行稳定性及稳态响应特性得到很大提升。

车轮跳动时，车轮绕瞬时转动中心摆动，因此轮距发生变化时车轮产生侧向滑移，增加轮胎的磨损。优化后侧向滑移量如图3e 所示，随车轮上下跳动侧向滑移量的变化量为18.44 mm，对比优化前减少了33.1%，变化量较少，满足设计要求，较好地减少了轮胎的磨损，提高了轮胎的使用寿命。

图3 优化前后车轮定位参数和前轮侧向滑移量的对比

麦弗逊悬架运动学优化前后的车轮定位参数变化量和车轮侧向滑移量如表4 所示，可以看出，车轮定位参数和侧向滑移量随车轮跳动的变化量显著减低，优化取得良好效果，提升了该车辆的操纵稳定性。

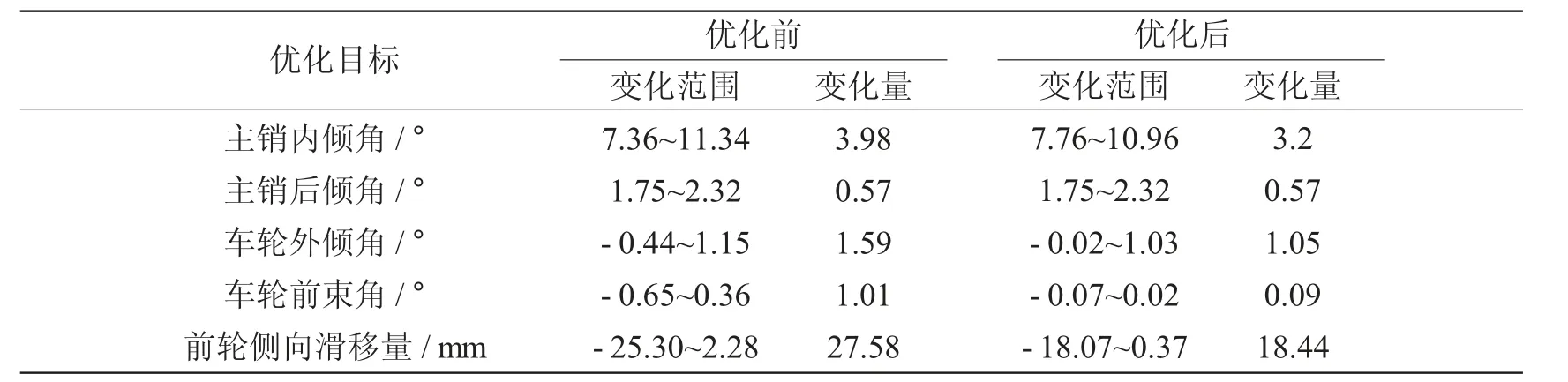
表4 优化前后车轮定位参数变量范围

3 结论

（1）利用ADAMS/View 建立了麦弗逊前悬架模型，以车轮定位参数和车轮侧向滑移量为研究对象，采用容限法计算得到车轮定位参数的权重，通过加权组合各子目标建立统一优化目标函数，通过灵敏度分析筛选优化设计变量，根据干涉条件及导向机构布置性能要求约束变量范围并添加约束条件，利用二次规划算法对其运动学特性进行仿真优化。

（2）优化后车轮定位参数和车轮侧向滑移量随车轮跳动的变化量显著减少，优化取得较好效果，其中主销内倾角的变化量减少了19.6%，主销后倾角的变化很小但处于合理范围，主销倾角的合理变化提高了转向轮自动回正的能力和转向轻便性。车轮外倾角和前束角的变化量分别减少了34%和91.1%，满足理想的前束变化特性和外倾变化范围，提升了整车的直行稳定性和稳态响应特性。车轮侧向滑移量随车轮跳动的变化量减少了33.1%，减少了轮胎的磨损，增加了轮胎使用寿命。该方法对悬架运动学特性参数的优化具有重要的参考意义。