LED 位置误差对傅里叶叠层显微成像质量影响与校正研究

朱斯聪，罗佳雄，陈汉宝，吴若非，甄均锐，伍雁雄*

（1.佛山科学技术学院机电工程与自动化学院，广东佛山 528225；2.佛山科学技术学院 物理与光电工程学院，广东 佛山 528225）

随着光学显微镜技术的进步，具有高分辨率与大视场的成像系统在生物医学研究、疾病预防与工业表面检测领域中扮演着重要的角色［1-2］。然而在传统的光学成像系统中，大视场与高分辨率是难以同时实现的。作为新崛起的显微成像技术，傅里叶叠层显微（FPM）技术能够解决这个难题。FPM 相对于其他超分辨技术的优点是设备简单、成本低［2］。典型的FPM 系统基本原理是使用微控制器依次点亮LED阵列不同位置的灯，同时利用相机采集不同位置的低分辨率图像，最后通过相位恢复算法将一系列低分辨率图像的频谱在频域中进行拼接，最终得到一张宽视场的高分辨率图像［3-4］。

但是当前该技术还存在一些不足，例如重建的高分率图像质量容易受到LED 位置误差的影响［5-6］。2016 年南京理工大学SUN 等人［7］首先指出FPM 成像质量会受LED 阵列位置误差的影响。当LED 阵列位置偏移较大时，重建的图像就会出现褶皱和伪影。LED 位置全局偏差主要来源于测量误差和安装LED 阵列时产生的误差，其中高度误差是由测量仪器精度造成的，而平移误差和旋转角度误差是由安装LED 阵列时造成的。由于LED 阵列的安装精度有限，这就使LED 的实际位置与理想位置不同，从而降低重建图像的质量。LED 位置误差会将错误的信息带入捕获的低分辨率图像，在FPM 中，这是必不可少的系统误差［8］。因此研究LED 位置误差对于提高重建图像的质量具有重要意义。

本文的工作如下：首先建立LED 位置失配比模型，其次通过仿真研究LED 位置偏移量对FPM 成像质量的影响，并确定LED 矩阵大小为3×3 的位置误差容许范围。为了解决LED 阵列的安装精度有限问题，本文提出一种基于对称图像强度分布的位置对准方法，该方法的原理是根据对称位置的低分辨率图像强度分布来估计LED 位置。最后通过实验对该方法的有效性进行验证，结果表明该方法能降低LED 阵列装调时产生的位置误差。

1 LED 位置误差分析

在研究LED 位置误差对FPM 成像质量的影响之前，首先在典型的FPM 系统模型中建立LED 位置坐标。接着通过LED 元件的位置确定入射光的波矢。入射光的波矢量是由FPM 中的LED 阵列和样品之间的相对位置决定的，计算每个LED 的照明波矢时，需要确定LED 阵列和样品位置的坐标。在分析LED 位置误差之前，应该建立一个错位模型，其模型如图1 所示。在理想位置的LED 阵列中，设LED灯之间的距离为dLED，LED 照明区域的中心坐标为（x0，y0），则第m 行、n 列LED 的照明波矢（um，n，vm，n）可以表达为

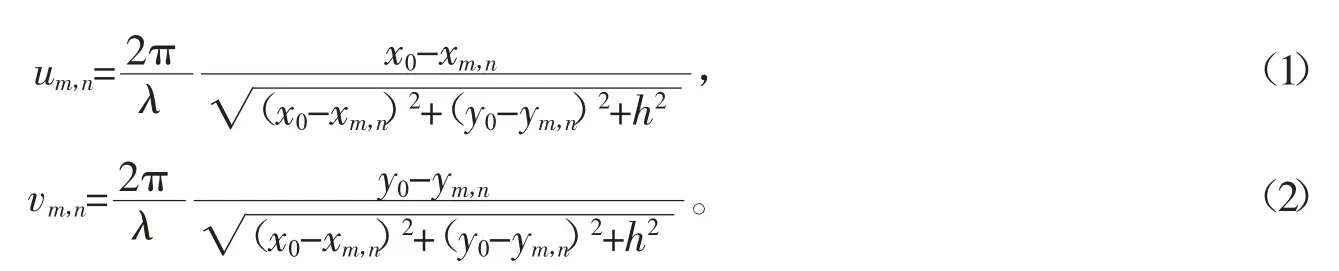
其中，λ 为LED 灯的照明波长，h 为LED 阵列与样品之间在垂直方向上的距离，xm，n和ym，n为第m 行、n列个LED 的坐标。

由公式（1）和图1 中的LED 空间坐标可知，LED 阵列位置主要包括高度h、平移x，y、旋转角度θ，这些参数都能改变波矢的大小和方向。波矢的计算会影响频谱圆在频域中的位置即改变光瞳函数获取样品原始位置的空间频率信息，从而导致相机采集的低分辨率图像的强度信息与在重建算法中理想位置的对应低分辨图像信息不一致，重建高分辨率图像的频谱不能以正确的低分辨率频谱信息去更新。这些参数的误差都会影响FPM 重构图像的质量。

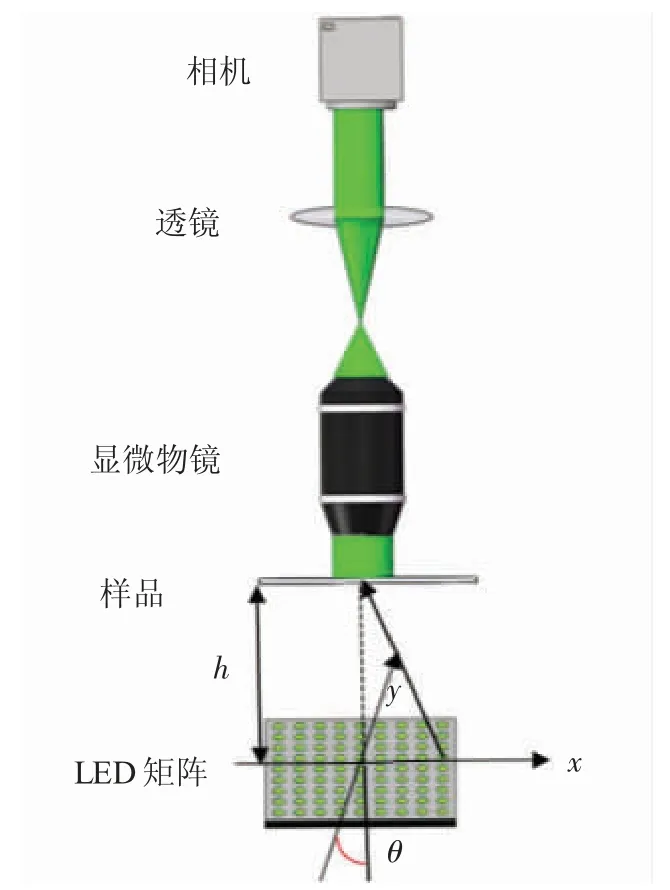
图1 带有位置误差的FPM 系统

当LED 阵列出现整体偏移时，假设LED 阵列的旋转角度为θ，LED 阵列沿x 轴和y 轴的平移量分别为Δx、Δy，高度偏移量为Δh。这时带有位置误差的LED 灯在x 轴和y 轴上的坐标可以表示为

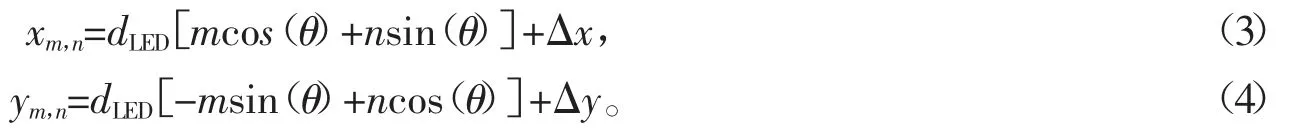
则入射光的波矢（um，n，vm，n）变为

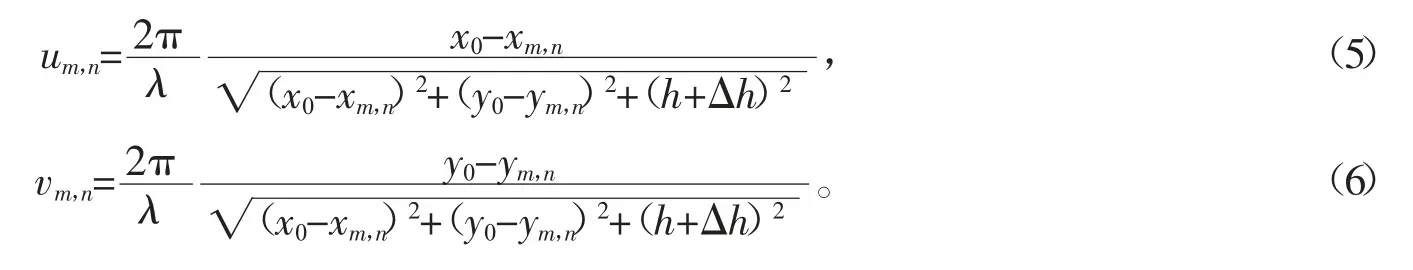
2 LED 位置偏移量对FPM 成像质量的影响

在研究降低LED 位置误差之前，需要对LED 位置误差进行定量分析，进而确定LED 位置误差对FPM 成像质量影响范围。本文在LED 位置误差模型和相位恢复算法基础上仿真分析LED 位置偏移量对FPM 成像质量的影响，确定LED 位置误差对FPM 成像质量的影响范围。

本次仿真的实验参数设计如下：LED 矩阵大小为3×3，波长为0.532 μm，高度为56.2 mm，像素大小为4.8 μm，间距为4 mm；并在该条件下仿真分析LED 位置偏移量对FPM 成像质量的影响。使用像素大小为500×500 的USAF 图像作为输入高分辨率图像，其图像如图2 所示。

图2 原始高分辨率图像

本次仿真使用均方误差（MSE）评价LED 位置误差对重构图像质量的影响，其评价方式是理想位置对应的低分率图像幅值与实际采集图像的幅值之间的均方误差，其对应表达式为

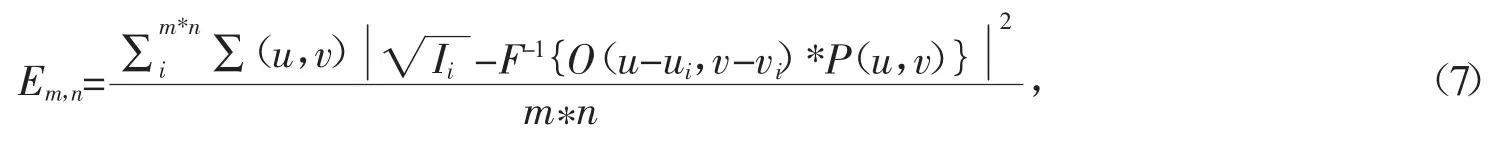
其中，Ii是带有位置误差的第i 张图像，F-1｛O（u-ui，v-vi）*P（u，v）｝是对应理想位置的第i 张图像，m*n 表示为采集图像的总数。

当LED 阵列位置只出现平移误差时，设其平移量为Δx 和Δy，研究其对重建图像质量的影响。本次实验将Δx 和Δy 的平移误差范围设为［-1 000 μm，1 000 μm］，平移误差对重建图像质量的影响结果如图3g 所示。

同理，当LED 阵列位置只出现高度误差时，通过仿真定量分析高度误差对重建结果的影响。设高度偏移量为Δh，其中Δh 的移动范围设为［-1 000 μm，1 000 μm］，高度误差对重建图像质量的影响结果如图3h 所示。当LED 灯分别与x 轴和y 轴方向不平行即出现夹角θ 时，研究旋转角度的误差对重建图像质量的影响。假设LED 阵列围绕中心LED 位置的旋转范围为[-5°，5°］，则旋转误差对重建图像质量的影响结果如图3i 所示。

由图3g 可知，当平移误差（Δx/Δy）在［-18 μm，18 μm］范围之内，MSE 的值不变即可以认为平移误差没有对重建图像的质量造成影响；由图3a、d、g 可知，当平移误差超过这个范围时，MSE 的值出现明显的变化即重建图像的质量受到平移误差的影响，其中振幅的图像背景出现褶皱和伪影现象，相位图像的部分信息会丢失。所以平移误差［Δx，Δy］的容许范围为［±18 μm，±18 μm］。同理，由图3b、e、h 和图3c、f、i 可知高度误差Δh、旋转误差Δθ 的容许范围分别为［-303 μm，262 μm］和［-0.26°，0.26°］。由图3g、h、i 可知3 种误差对重建图像质量的影响程度不同，其中平移误差对重建结果影响最大，高度误差对重建结果影响最小。该结果可以为后续降低LED 位置误差提供参考依据。在FPM 系统中，由于重构图像的质量对每个LED 位置很敏感，从而增加LED 阵列的装调难度。

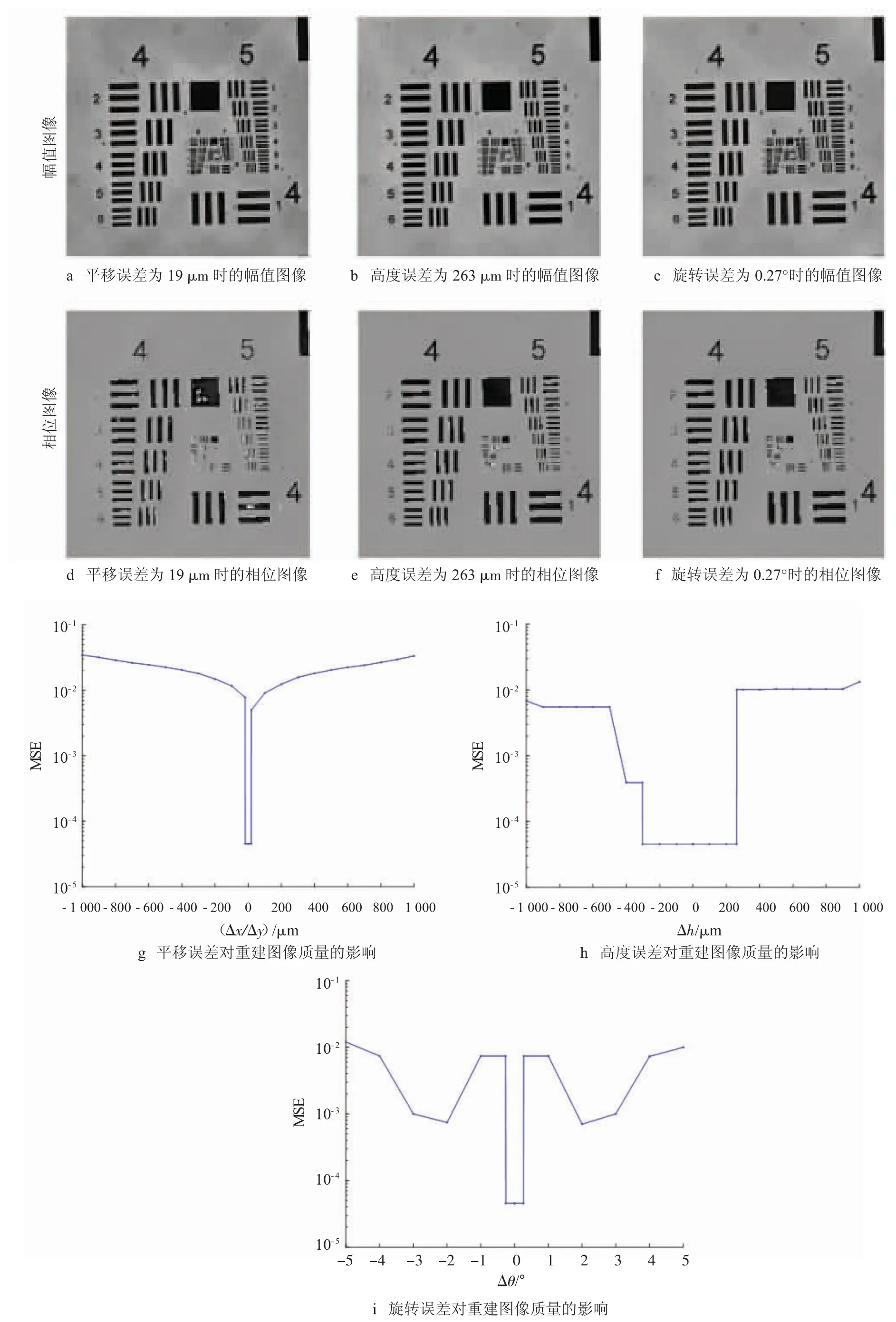
图3 LED 位置偏移量对重建图像质量的影响

3 LED 位置对准与实验分析

3.1 LED 位置对准方法

在FPM 系统中，LED 阵列中不同位置的灯珠发出的光可近似看作平面波，且每个LED 的光照强度是保持一致的。在曝光时间相同条件下，在对称照明角度下采集两幅图像的强度是相同的［9-10］，其中LED 光照强度随着照明角度的变化曲线如图4 所示［10］。当LED 阵列位置发生偏移时，传播到样本平面的入射光强度分布将发生改变。根据这个原理，本文提出一种基于对称图像强度分布的LED 阵列位置对准方法。

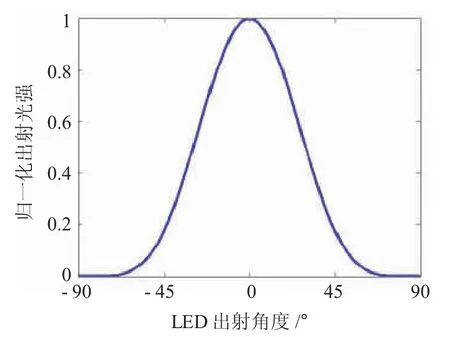
图4 LED 光强分布曲线

在相机采集图像之前，需要对LED 阵列进行安装。LED 阵列被固定在平移台上面，并在LED 阵列的平面上放置一个水平仪，调节平移台使其保持水平。在相机上面也放置一个水平仪，通过调整相机水平位置，使其保持水平，这样可以使相机传感器面与显微镜载物台平面平行，从而降低LED 阵列与样品水平面的旋转误差。然后调节平移台使LED 阵列达到所需要的高度，最后用游标卡尺测量高度的具体数值。

在载物台上不放样本条件下，依次点亮如图5 所示位置的LED 并保存采集的图像，然后通过本文提出的方法去校正这些图像的位置误差。该对准方法包含多种图像处理的算子如边缘检测、二值化、图像运算等。该对准方法是在图像处理基础上直接估计亮场图像的照明位置。设输入对称位置的明场图像强度分别I1和I2（其中I2是一幅图像经过图像运算翻转后的强度），当这两幅图像强度的差值达到最小即min（ΔI）=I1-I2时，则完成该图像对应位置误差的校正。该方法的对准过程如图6 所示。

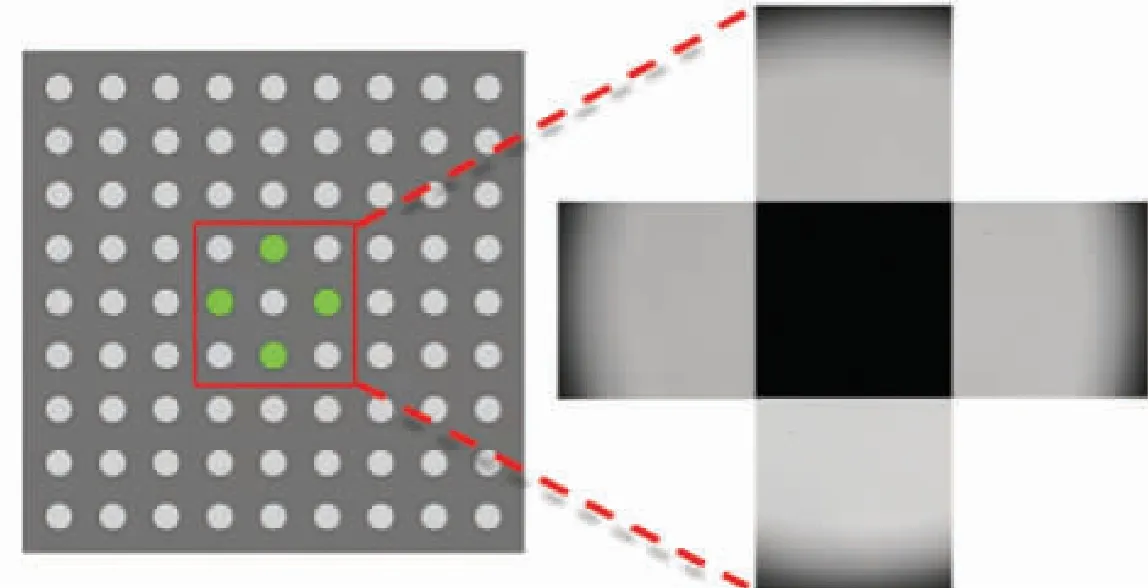
图5 LED 被点亮的位置示意图

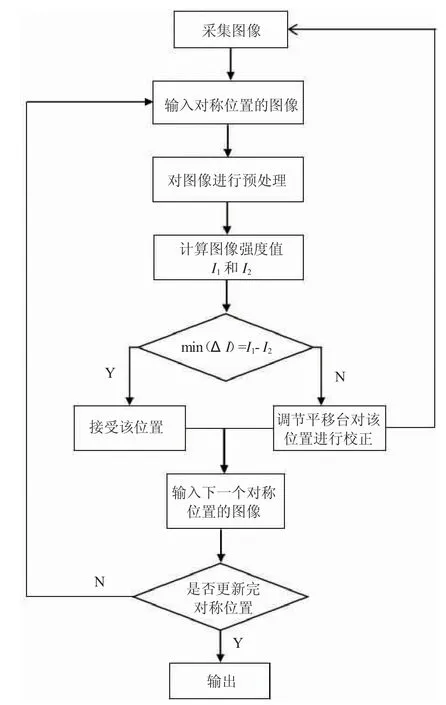
图6 LED 位置对准的流程

由于该方法的局限性和平移台调节精度有限，该方法的校正精度只能使x 轴和y 轴方向的平移误差（Δx，Δy）控制在10 μm 左右甚至更低，高度误差Δh 控制在100 μm 以内，旋转误差Δθ 控制在0.1°以内。所以该方法能降低LED 阵列装调时产生的位置误差，但不能消除LED 位置误差。

3.2 实验与分析

为了验证该方法的有效性，本文还搭建一个基于LED阵列照明的FPM 成像平台，该实验平台如图7 所示。选择带有奥林巴斯物镜的显微镜（放大倍数4X，NA=0.1）作为FPM 成像系统，使用一个16×32 的可编程LED 阵列（LED的间距为4 mm，波长为532 nm）作为照明光源。选择绿色通道照亮样品，LED 阵列与样品之间的距离为56.2 mm。采用像元大小为2.4 μm 的相机记录不同入射角下的低分辨率图像。在实验中，LED 矩阵大小为3×3，选择美国空军分辨率板（USAF1951）作为本次实验的样本，USAF1951 分辨率板被放置在由3D 打印的置物台上，并将其固定在二维载物台上。

图7 FPM 系统实物图

经过上述步骤的LED 阵列位置对准之后再进行本次实验。在该系统参数设计条件下，只需要采集9 个LED 灯对应的低分辨率图像，合成孔径达到0.2 NA，从而实现2 倍超分辨成像。该系统的极限分辨率为3.245 μm，成像分辨率理论值为1.62 μm（对应分辨率板第8 组元素2 和元素3 线对之间），低分辨率图像的像素大小为500×500。然后通过相位恢算法将采集的低分辨图像重建一幅高分辨率图像，其重建结果如图8 所示。

图8 USAF1951 在相位恢复算法中重建的结果

实验结果表明本文提出的方法通过AA 算法重建图像的质量较好，图像背景没有出现伪影和褶皱；重建图像的分辨率和清晰度都有明显的提高。其中，重建图像的分辨率能达到第8 组元素2，对应的分辨率为1.74 μm。所以该方法可以降低LED 阵列位置的装调难度。

4 结论

为了研究和降低LED 位置误差对FPM 成像质量的影响。首先，本文建立LED 位置误差模型和通过仿真分析LED 位置的偏移量对重建图像质量的影响，并确定LED 矩阵大小为3×3 的位置误差容许范围。然后，为了降低LED 阵列的装调难度，本文提出一种新的LED 阵列位置对准方法。最后，通过已搭建的FPM 成像系统验证该方法的有效性，实验结果表明该方法重建图像具有较好的质量。但是该方法的对准精度容易受到LED 光照强度和平移台调节精度的影响。基于本文方法不足之处的改进将是未来工作的研究方向。