负电容压电分流的圆环超构材料隔振

林丽芳， 陆泽琦， 丁虎， 陈立群

(1.上海大学 力学与工程科学学院， 上海 200444； 2.上海大学 上海市能源工程力学重点实验室， 上海 200444； 3.上海市应用数学和力学研究所， 上海 200072)

随着隔振技术的进一步发展，在航空航天及船舶领域中隔振技术高稳定性、高指向精度的要求进一步提高，研究高性能隔振日益成为瓶颈难题，需要发展新的力学原理来解决[1-3]。减振和隔振是传统的振动理论，随着控制理论的发展，用力电耦合系统来控制振动成为一种重要的方式，这种方法具有成本低廉、容易实现的特点，但也存在频率范围窄、兼容性差等问题[4-5]。因此在这一理论基础上，本文引入超构材料与分流电路结合，可进一步提高隔振设计水平。

压电分流电路振动控制的理论是由Forward[6]提出的，其原理是通过压电片将系统振动所产生的机械能转化为电能，并通过分流电路对其进行有效抑制。Hagood等[7]对此方法进行了拓展研究，给出了RL分流电路的数学模型，引起了众多学者的关注。研究发现基于RL压电分流电路构成的控制系统重量和体积都很小，但电阻和电感值的选取十分有限，因此其减振频率范围十分有限。Park等[8]通过负电容分流电路研究控制了悬臂梁多阶模态振动，在0～3 000 Hz频率范围内实现了有效的振动衰减。Berardengo等[9]提出了当电路设置越接近稳定性极限时的振动控制效果越好。Billon等[10]研究了一种压电元件与机械放大器结合的悬挂结构，并利用基于电阻和负电容的不同分流器降低振动在宽频带内的传输。Ji等[11]提出了一种基于负电容并联电路的同步开关阻尼方法，实现非对称双极电压振动控制以提高控制性能，最终通过实验验证所设计电路的优良阻尼性能，负电容分流电路不仅具有传统分流电路的优点，还具有宽频的特点，极大方便了工程应用[12-15]。

超材料是一种设计用于调控弹性波的人工复合材料。因性能优于传统材料，研究开发热度迅速增长，例如负折射、负泊松比、负刚度和负体积模量等[16-17]。预计超材料将为推进隔振降噪技术发展提供前所未有的机遇[18-24]。在声子晶体中，带隙是由布拉格散射现象产生的[25-26]，其波长与周期性的空间尺度相关，因此低频时则需要较大的结构来产生带隙，其带隙通常出现在中高频范围内[27]。而在低频范围(低于布拉格反射条件)和相对较小的结构中可以产生局域共振带隙[28]。赵龙等[29]通过周期性放置转动能量采集谐振器，设计产生了局域共振带隙，实现振动隔离和能量采集一体化。而压电材料与超材料结合后能够产生特殊的力电耦合特性，这种方式已被广泛应用于调整超构材料带隙[30-31]。Sugino等[32]研究了一种控制一维局域共振压电超材料无序性的优化方法，可有效提高衰减带隙宽度同时避免振动能量沿结构方向的局部化。何清波等[33]提出了一种刚度-质量编码新材料，为低频宽带隔振的可调谐性提供新思路，并在相关工程应用中展现潜力。Chen等[34]提出了一类具有负电容压电分流的新型活性弹性超材料，发现通过使用具有不同负电容值的压电贴片可有效地调谐感应带隙，这类材料尤其适用于极低频情况。Wang等[35]设计了一种可嵌入电磁铁的3D打印数字超材料，并从理论和实验上研究了其机制，实现可编程的扩大超材料带隙。

受到以上研究的启发，本文构造了一种周期性铺设有外接负电容分流电路的压电纤维的圆环超结构，推导了力电耦合动力学方程并通过有限元软件分析了该结构的减振特性。

1 带有负电容分流阻尼器的悬臂梁的力学行为

1.1 机电耦合系统建模

分流电路会产生一个新的阻尼用来增强振动压电梁系统的固有阻尼。该电路通过一对压电片连接到悬臂梁上。压电分流阻尼的基本思想是通过压电传感器将振动结构中的机械能转化为电能。图1(a)显示了与压电相连的负电容分流阻尼器的电路原理图，其等效电路图如图1(b)所示。

如图1所示，压电片可以等效为一个交流电源Ve(t)和一个串联的电容器Cp。电阻器R1、R2、电容器C1以及运算放大器可构成一个传统的负电容分流电路。电阻器Rs的设置是为了避免一些电气问题，但其设置也会导致一些不稳定因素。因此，有必要设置电阻R3来避免这些不稳定因素。因此，负电容分流阻尼器可以简化为一个等效电阻Req和一个等效电容-Ceq并联的形式。其表达式可以写为：

Ceq=CnR2/R1

(1)

(2)

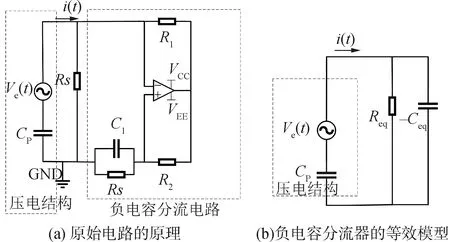
图1 带有负电容分流器的压电的电路模型Fig.1 Circuit model of a piezoelectric with a negative capacitance shunt

建立了一个如图2所示的模型来描述压电梁系统的弯曲振动。压电陶瓷和悬臂梁被认为是完全粘合在一起的，通过哈密顿建立压电悬臂梁的动力学方程：

(3)

假设在压电梁横截面上的所有点的横向位移都是一样的。对于Bernoulli-Euler梁，忽略了梁的剪切变形和旋转惯性。由于压电片是对称配置的，假设其纵向位移为零。

图2 压电梁系统的结构示意Fig.2 Schematic diagram of the structure of the piezoelectric beam system

其动力学方程可表述为：

ϑV[H(x-x1)-H(x-x2)]=f(x,t)

(4)

(5)

式中：H为Heaviside函数；w为悬臂梁的挠度；ρb、ρp和Ab、Ap分别对应悬臂梁和压电陶瓷的密度及横截面面积；Ib和Ip为关于中性层的极惯性矩；R为等效阻尼；Cn、Cp分别表示负电容及压电陶瓷的固有电容；ϑ为机电耦合系数；V为压电陶瓷输出电压；x1、x2为压电陶瓷两端沿悬臂梁轴向的位置坐标。

从以上分析可以看出，方程(4)是一个四阶偏微分方程。假设梁的响应可以写为：

(6)

基于边界条件，其模态的形式可以写为：

Φ(x)=cos(αix)-cos(αix)-βi(sinh(αix)-

sin(αix))

(7)

将方程(6)代入方程(4)，离散化的微分方程可写为：

(8)

式中：

H(x-x2)]dx

(9)

(10)

H(x-x2)]dx

(11)

(12)

(13)

式中：M、C、K分别代表悬臂梁的模态质量矩阵、模态阻尼矩阵和模态刚度矩阵；Fb是外部激励；Fp表示压电片对梁的激励作用。

1.2 有限元分析

为了验证负电容分流电路的对振动的抑制效果，可以通过有限元仿真来实现，如图3所示。在此仿真中，悬臂梁的材料是铝，压电陶瓷的材料是PZT-5A，它们的几何参数及材料参数分别如表1和表2所示，a代表压电陶瓷中电极宽度，p代表电极周期。

系统相应的频率响应函数如图3所示。可以看出，在负电容分流电路的作用下，悬臂梁的振动在0～3 000 Hz的频率范围内，这些阶次的振动被更明显地衰减。振幅随着频率的增加而逐渐减小。考虑负分流电路的损耗率方程，就可以很容易地解释这一现象。而随着频率的增加，机械阻抗的损失因子也会增大。

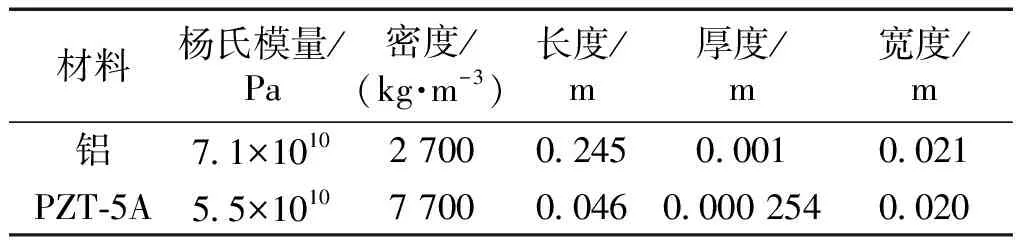
表1 悬臂梁和压电陶瓷的几何和材料参数

表2 压电陶瓷的电参数[36]Table2 Electrical parameters of the piezoelectric ceramic[36]

图3 压电梁系统的仿真频率响应Fig.3 Simulated frequency response of the piezoelectric beam system

2 周期性分布有负电容分流电路的超材料圆环结构的振动控制效果

2.1 建模

图4显示了一个带有周期性分布的压电纤维片的圆环超材料结构，每个压电纤维片均与负电容分流电路相连。在下面的推导中，旋转惯性和剪切变形将被忽略。且圆环的横截面是矩形的，且沿轴向恒定。

图5表示圆环结构的一个单元abcd，作用在这个单元上的径向和切向惯性力可分别表示为：

沿环的径向和切向的运动方程可分别写为：

(14)

(15)

式中：F是剪力；P是拉力；ρ为密度；A是横截面积；R是圆环中心线的半径；f和p分别是径向和切向外力；u和w分别代表径向和切向位移。

圆环中性面上的运动力矩方程可写为：

(16)

为了利用变形分量来表示力和力矩，我们考虑一个典型的环形单元ab，它位于离环形中心轴一定距离的x处，如图6所示。假设该单元的轴向应力为σ，轴向应变为ε，所以两者满足关系：

σ=Eε

(17)

式中E为圆环结构的杨氏模量。

轴力P和弯矩M可以写为：

(18)

(19)

图4 负电容压电超材料环模型Fig.4 Model of a metamaterial ring with negative capacitance piezoelectric ring

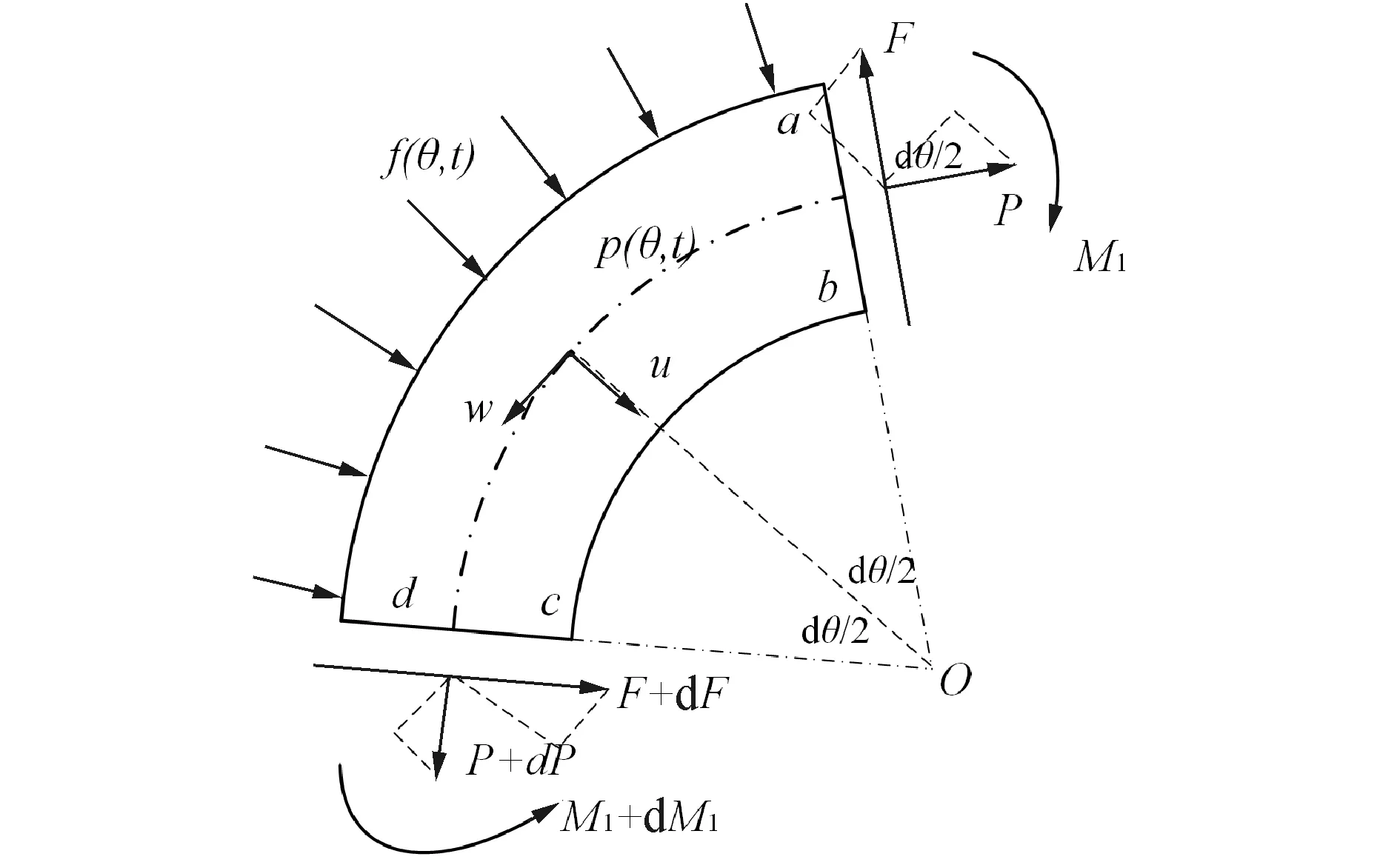
图5 圆环的一个单元Fig.5 Element of a circular ring

图6 弯曲梁的微分单元Fig.6 Differential element of a curved beam

单元应变可以表示为：

(20)

通过代入方程(17)和方程(20)到方程(18)和方程(19)中并积分，可以得到：

(21)

(22)

式中I表示关于横截面的极惯性矩，可以表示为：

(23)

由于环形中心线的不可扩展性条件，并忽略少量的阶次，可以得到：

(24)

将式(24)代入式(22)中，因此方程(22)可以写为：

(25)

从该式可以看出，当半径无限大时，式(25)为直梁弯矩。

综上，平面内振动圆环的动力学方程为：

(26)

同悬臂梁一样，电路控制方程为：

(27)

周期性排列负电容分流电路的圆环的动力学方程可以写为：

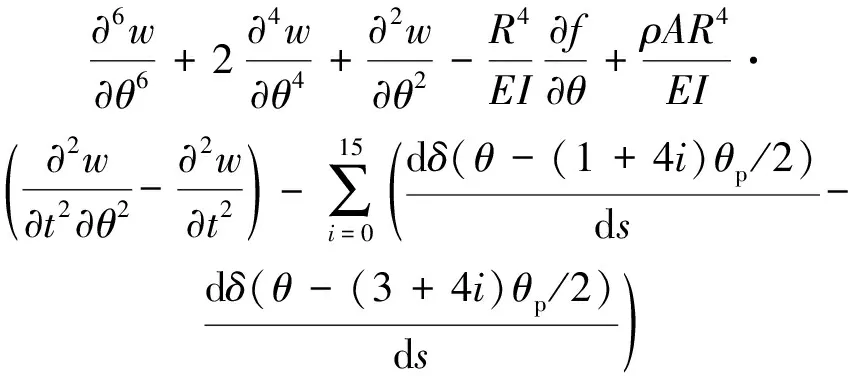
(28)

(29)

2.2 有限元分析

为了探究负电容周期性超材料圆环的减振特性，采用有限元方法对其进行频率响应分析。以圆环为出发点，进行了负电容和超材料2种物理机制的复合。在超材料圆环的顶部施加了指定位移激励，在底部计算其幅频响应。圆环结构参数如表3所示。压电纤维片的电参数以及结构参数如表4所示。

表3 超材料圆环结构参数Table3 Structural parameters of metamaterial ring

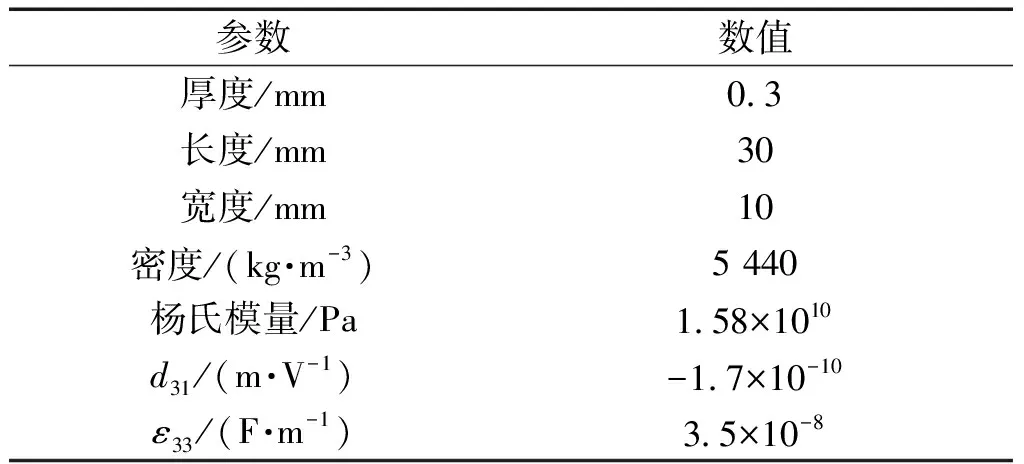
表4 压电纤维片的电参数及结构参数[37]

等效电阻值取-2 kΩ，等效电容值取-50 nF时的频率响应图如图7所示，在没有连接负电容分流电路的情况下，圆环表现出周期性超材料特性，出现较明显的带隙，但带隙较窄。连接负电容分流电路后，圆环不仅表现出超材料结构特性，出现较宽的带隙，且其减振效果十分明显。可以看出在低频范围内，减振效果存在但微弱，频率达到1 000 Hz以上时，共振峰被压下来，振动得到显著抑制。在此基础上，本文进一步对负电容分流电路进行了参数影响讨论。

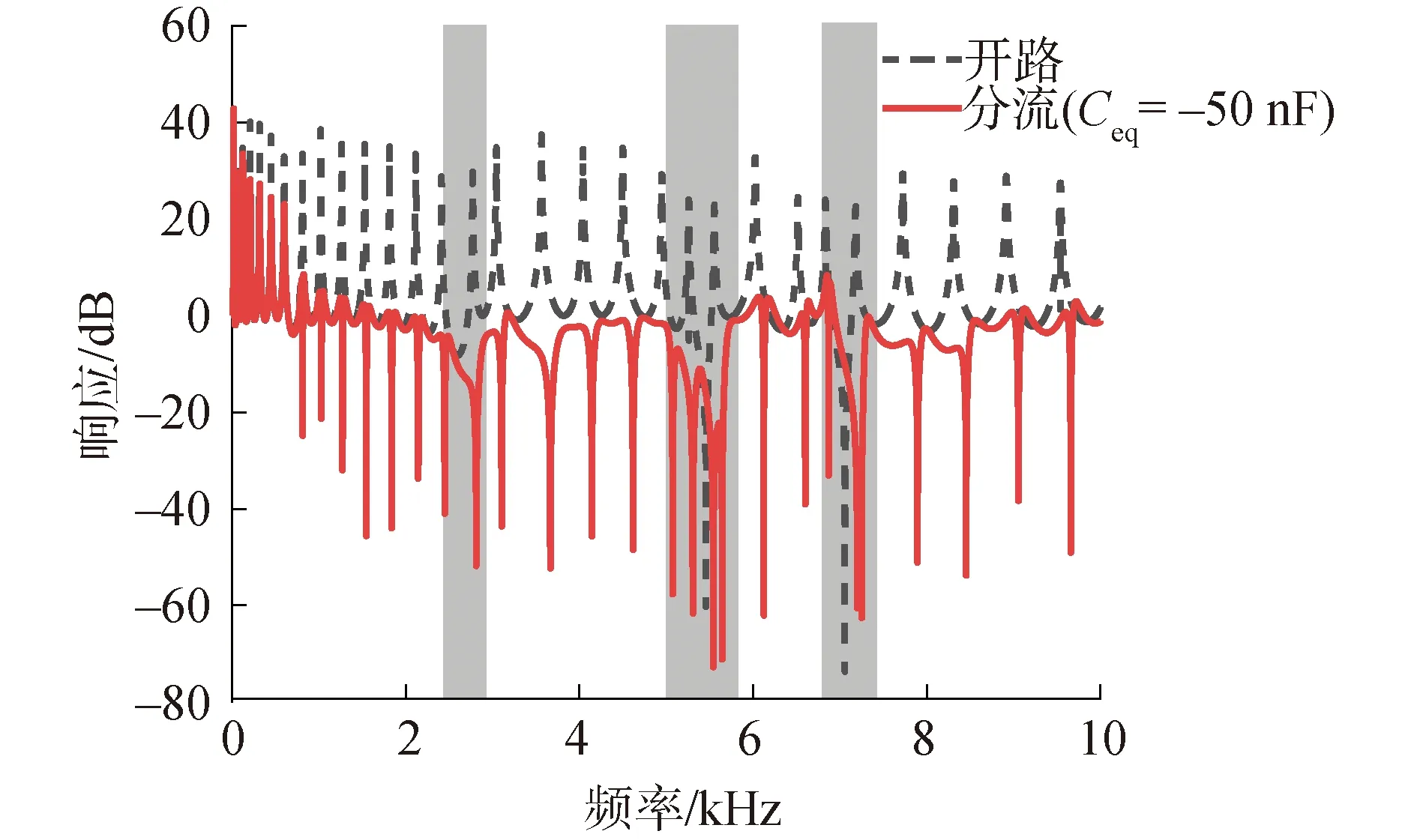
图7 周期性负电容超材料圆环幅频响应曲线Fig.7 Amplitude-frequency response curves of the periodically arrayed negative capacitance metamaterial ring

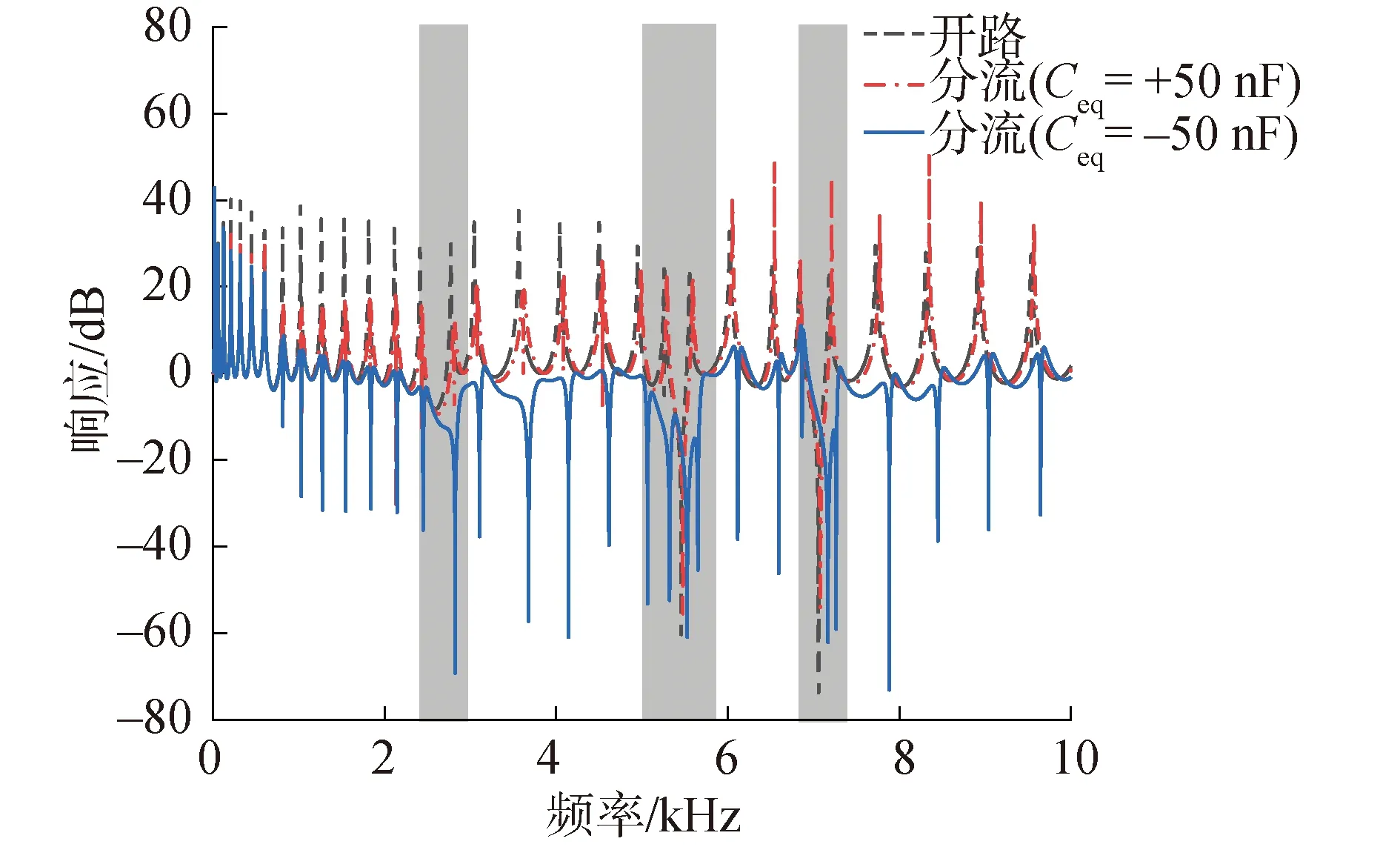
图8 Ceq取+50 nF和-50 nF时的频率响应曲线Fig.8 Frequency response curves forCeq at +50 nF and -50 nF

等效电容Ceq的值分别取+50 nF和-50 nF时的超材料圆环幅频响应曲线图如图8所示。从图8可以看出，正电容情况下的超结构，减振效果不是很明显且带隙极窄。而负电容情况下的超结构，出现较宽带隙，振动明显被抑制。这也从侧面反映出了负电容分流电路在减振工作中的可行性。

等效电容分别取-40、-50、-60 nF时的幅频响应曲线图如图9所示。从图中可以看出，低频段时，等效电容为-50 nF时的减振效果最优，而在高频段时，等效电容为-60 nF时的减振效果最优，但两者减振效果均优于等效电容值取-40 nF的情况。这也从侧面说明，当等效电容与压电纤维固有电容绝对值之比越趋近于1时，等效电路的减振效果最好。

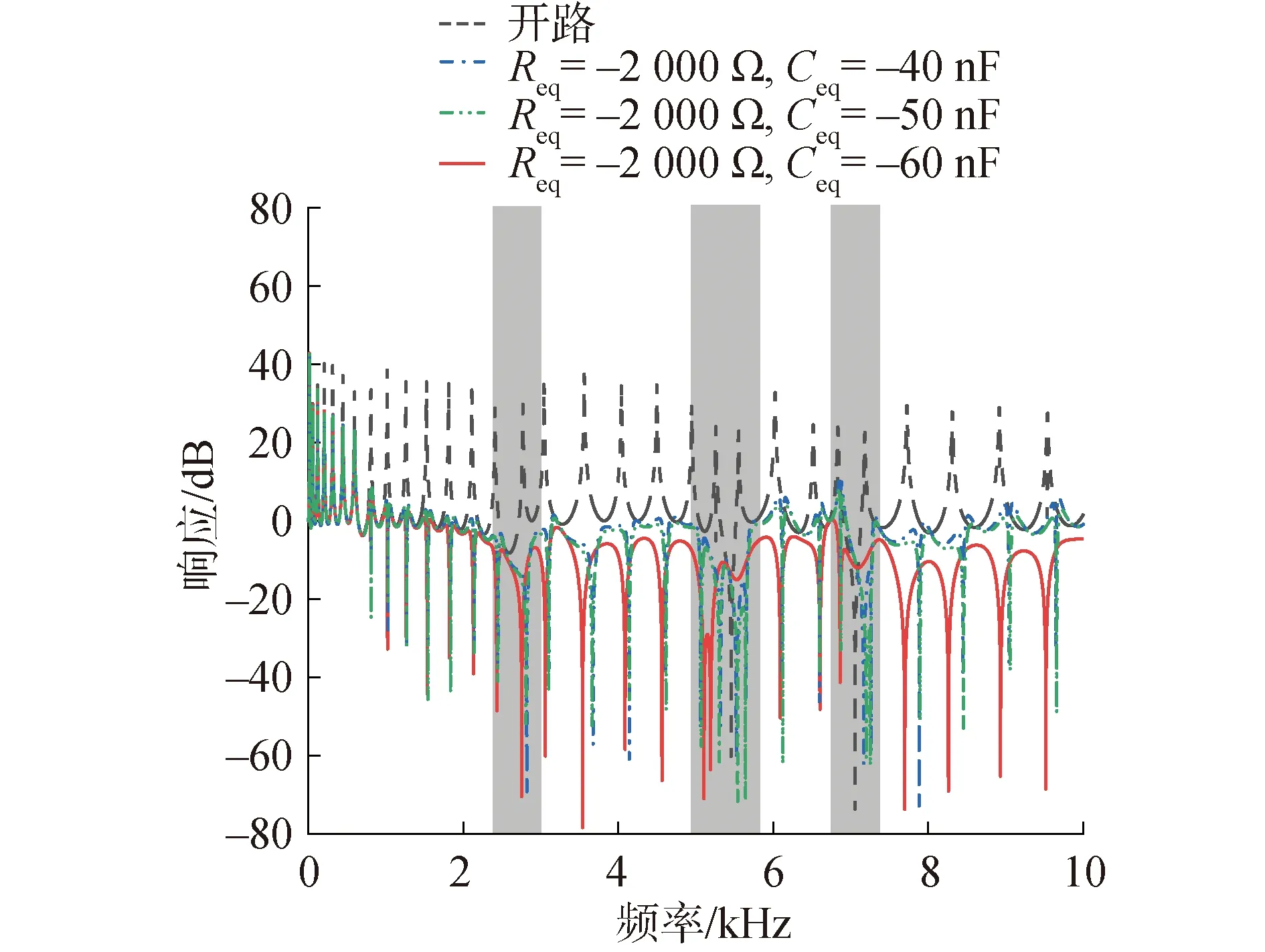
图9 Ceq取-40 nF、-50 nF及-60 nF时的频率响应曲线Fig.9 Frequency response curves forCeq at -40 nF, -50 nF and -60 nF

圆环厚度的值分别取0.8、1.0和1.2 mm时的超材料圆环幅频响应如图10所示。从图10可以看出，圆环厚度为0.8 mm时产生了2 000～2 500 Hz、6 000～6 500 Hz、9 000～10 000 Hz 3个频率范围的带隙，圆环厚度为1.0 mm时的带隙范围分别为2 500～3 000 Hz、5 000～6 000 Hz和7 000～7 300 Hz，圆环厚度为1.2 mm时的带隙范围分别为3 000～3 500 Hz和7 000～7 300 Hz。可以看出，随着圆环厚度的减小，一阶带隙的频率范围向低频移动，同时，在相同的频率范围(1～10 kHz)内，0.8 mm厚度的圆环在高频处产生了新的带隙。考虑到带隙的带宽与稳定性，本文所研究的圆环厚度取为1 mm。

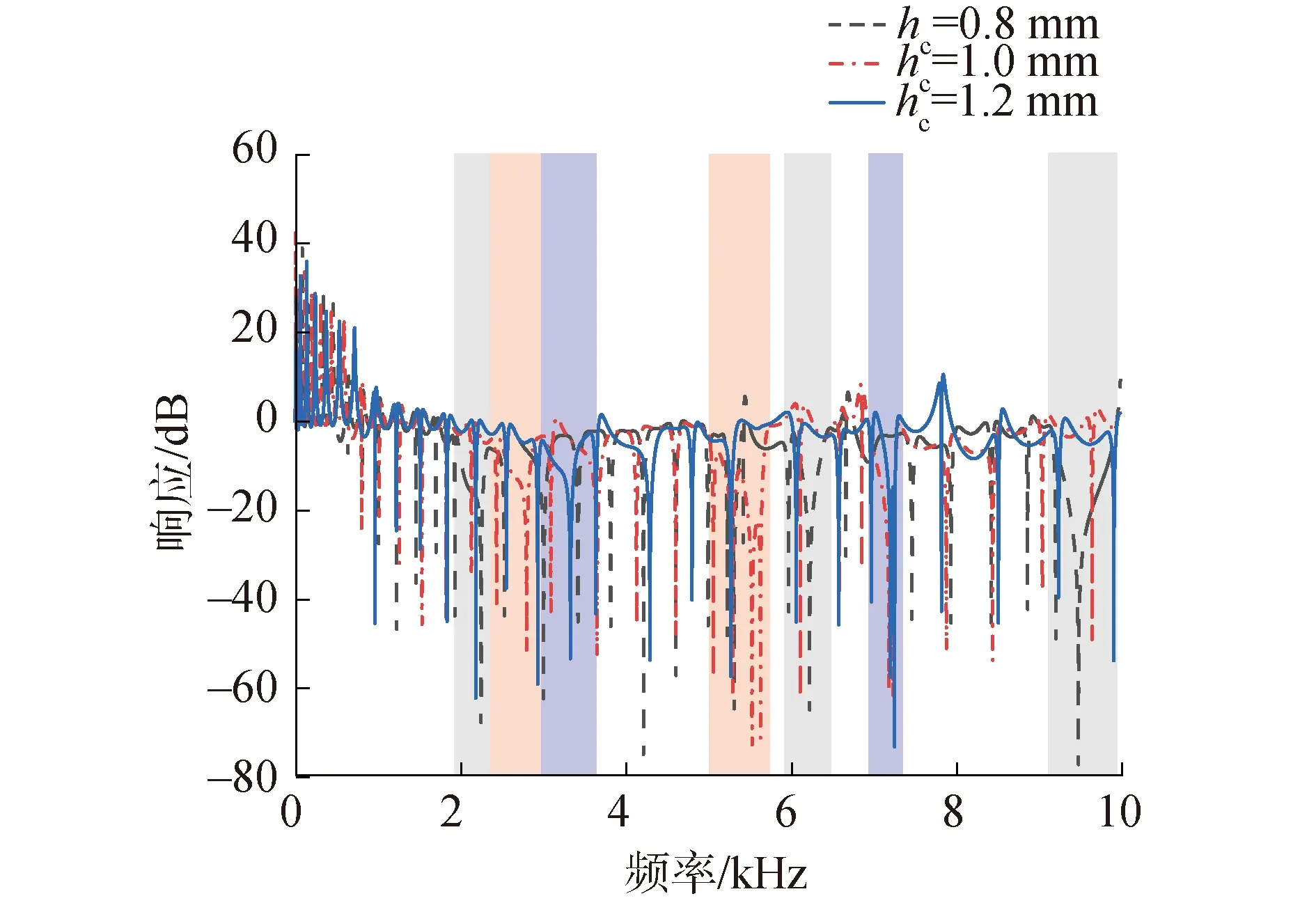
图10 圆环厚度取0.8 mm、1.0 mm和1.2 mm时的频响曲线Fig.10 Frequency response curves forhc at 0.8 mm, 1.0 mm and 1.2 mm

压电纤维片厚度分别取0.25 mm和0.30 mm时的幅频响应如图11所示。从图中可以看出，压电纤维片的厚度为0.30 mm时的超材料圆环的隔振性能显著优于压电纤维片厚度为0.25 mm时的超材料圆环，且在5 000～6 000 Hz的频率范围内，前者的带隙宽度显著宽于后者，基于此，前文研究所采用的压电纤维片厚度均为0.30 mm。

图11 压电纤维片厚度取0.25 mm和0.30 mm时的频响曲线Fig.11 Frequency response curves forhp at 0.25 mm and 0.30 mm

3 结论

1) 将负电容分流电路应用于悬臂梁时，振动得到显著衰减，负电容分流电路在隔振领域具有可行性。

2) 负电容分流电路周期性铺设在圆环结构时，出现明显带隙，且负电容分流电路的加入使得振动得到显著衰减且带隙变宽。

3) 通过电路参数分析可以发现，当等效负电容与压电纤维固有电容绝对值之比趋近于1时，隔振效果最好。

但由于计算时所作运算及仿真均基于等效电路，与实际电路相比略有误差，需要后续更深入的研究。