周期性矩形管浮筏结构的振动分析

朱自强， 李爽， 曲嘉

(1.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001； 2.哈尔滨工程大学 青岛创新发展基地，山东 青岛 266400)

随着舰船设备的不断发展，对于舰船减振降噪的需求也越来越高[1]。常见的减振措施主要分为主动减振和被动减振2种[2]，前者通过对发动机等设备进行改进，减少振源处的振动产生；后者则是在振动传播的路径上设置减振装置，阻断或减少振动的传播。被动减振因结构简单、可靠性强在减振领域得到广泛的应用，浮筏减振系统[3]作为被动减振的主要方式长期以来备受国内外学者的关注。目前浮筏减振系统的传统结构包括桁架式结构、箱体式结构、周期结构[4-5]等。

周期性变化的结构由于对弹性波具备衰减域特性 (又称为带隙特性) ，对于某些频段的弹性波具备优异的隔离能力，在浮筏减振系统研究领域受到广泛关注。对于工程中常用的周期结构，国内外诸多学者从理论、数值模拟和实验方法进行了讨论。SONG[6]、Y. FANG[7]、D. Richard[8]等对周期梁、板和壳的振动特性提出了新算法，此外Wang等[9]将周期结构应用于浮筏减振中，并利用遗传算法对其进行优化，周期性结构相比传统浮筏结构具有更优异的减振效果。况成玉[10]与程世祥[11]通过数值模拟和实验分别对桁架浮筏与曲梁浮筏的振动衰减特性进行了研究，结果表明2种结构均表现出良好的带隙特性和高频减振效果。徐时吟[12]将六韧带手性结构引入到筏架设计中，并通过有限元与实验的方法证明其较传统浮筏有更好的减振效果。此外基于声子晶体理论，温激鸿、沈惠杰[13-16]等对典型工况构建了具有带隙特性的周期性结构，研究表明周期结构在带隙内具备良好的减振效果，并将此种结构应用到浮筏减振系统中。杨德庆等[17]将负泊松比结构应用于浮筏系统，分析其减振效果，结果表明负泊松比筏体可显著降低筏架重量，同时在某些频段能提高浮筏的振级落差。

根据以上对周期性结构的研究，可发现周期性结构相比于传统浮筏结构具备优良的减振效果，同时添加负泊松比的筏体具有轻量化、高减振效果、高降噪性能。此外负泊松比夹芯结构因其芯子层独特的变形形式被广泛应用于抗冲击、抗爆炸领域。然而负泊松比结构的制备方式较为复杂，故本文采用周期性排列的矩形管设计了在压缩载荷下具备负泊松比特性的夹芯结构，同时将负泊松比夹芯结构与浮筏隔振系统进行结合。为研究该结构的变形形式和振动传递特性采用数值模拟方法在位移压缩载荷下分析了该结构的变形形式，同时在频率0～1 500 Hz以及激励100 N下，分析了该结构的模态响应和位移振级落差，最后研究了矩形管在不同层数、不同梯度排列方式和不同单胞壁厚下对结构振动传递特性的影响。

1 周期性矩形管浮筏结构有限元模型

本文通过ANSYS Parametric Design Language(APDL)对周期性矩形管浮筏结构进行静态压缩和振动谐响应的数值模拟分析。浮筏整体结构采用solid186单元进行模拟，面板材料和芯子层材料均采用304不锈钢，结构各部分参数如图1所示。

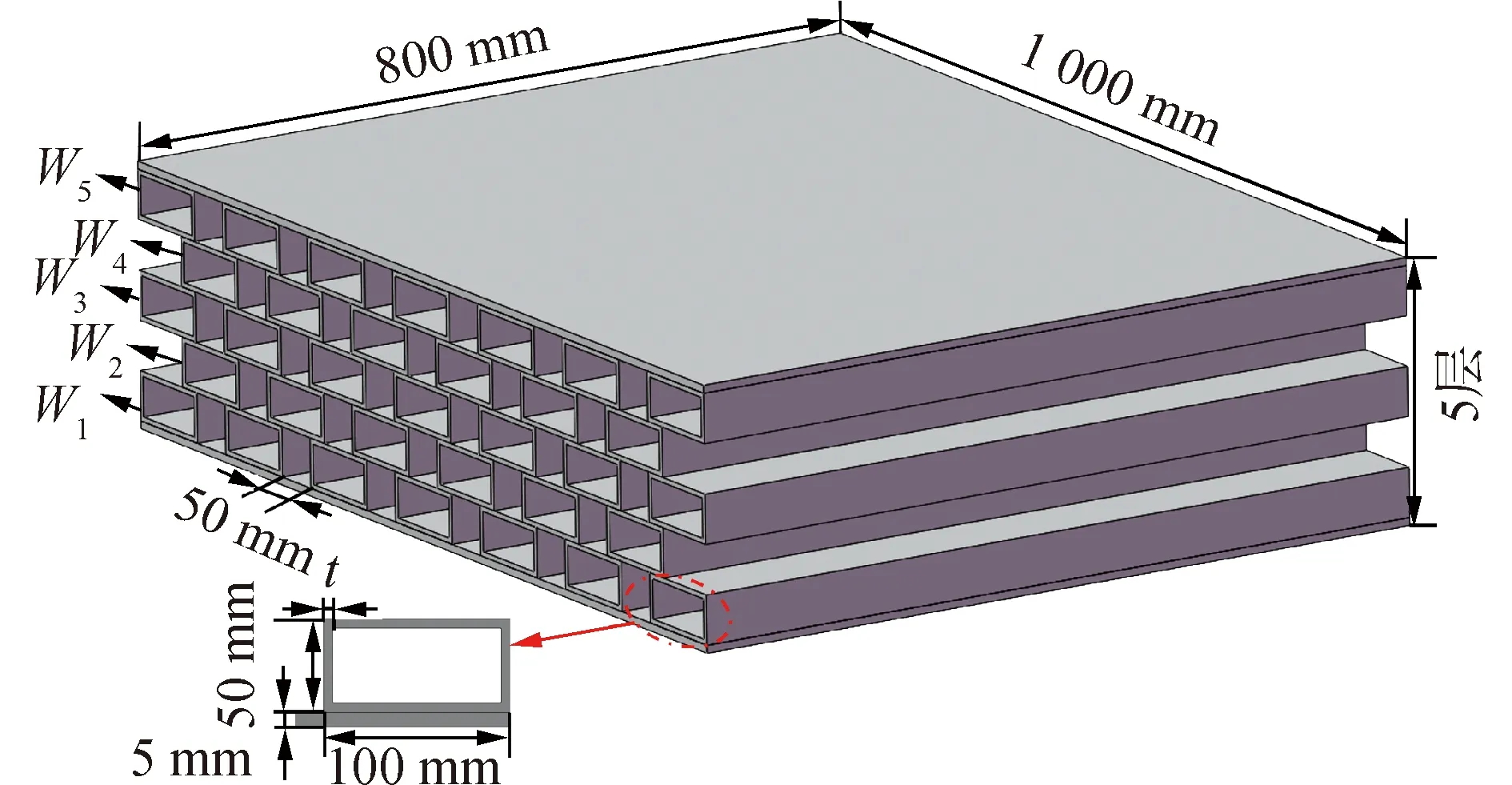
图1 周期性矩形管浮筏结构各部分尺寸标注Fig.1 Dimensions of foating raft structure with periodic rectangular tubes

整体结构采用6面体单元进行划分，如图2(a)所示，其中单个网格最小尺寸为结构中最小壁厚尺寸，最大尺寸为20 mm。在静态压缩部分为分析该结构的最终变形形式，采用Johnson-Cook本构模型对其进行模拟分析材料参数见表1[18]。同时在下面板施加固定约束，在上面板施加位移载荷，有限元模型如图2(b)所示。

图2 周期性矩形管浮筏结构有限元模型Fig.2 Finite element model of floating raft structure with periodic rectangular tubes

表1 304不锈钢材料参数Table1 Material parameters of304 stainless steel

在振动分析中，仅考虑该结构芯层参数对其传递特性的影响，故仅在该结构左侧施加固定约束，同时在上面板中心处施加100 N向下的激励，在0～1 500 Hz内分析该结构的振动传递特性，响应点为下面板中心处，有限元模型如图2(c)所示。

本文通过Tdb(位移振级落差)来表征周期性矩形管浮筏结构的振动传递特性：

(1)

式中：Tdb为位移振级落差；XRE是响应点位移；XF为激励点位移。

当Tdb>0时表示结构将振动响应放大，当Tdb<0时表示振动响应得到衰减。

2 静态压缩下浮筏结构的变形形式

通过对该结构的静态数值模拟，提取上面板合力为压缩位移并根据式(2)和式(3)得到：

(2)

(3)

式中：σ和ε分别为结构的等效应力和等效应变；F为上面板受到和合力；A为上面板的横截面积；ΔH为上面板的压缩位移；H为结构的高度(W1+W2+…+Wn)。

结构的等效应力应变曲线如图3所示，大致分为初始阶段、收缩阶段、变形阶段和密实阶段4个部分，对比结构的变形形式和等效应力-等效应变曲线，在应变为0.02、0.15、0.3和0.7分为提取收缩阶段、变形阶段和密实阶段的应力云图以及4个阶段对应的范围如图3所示。

图3 结构的等效应力-等效应变曲线Fig.3 The equivalent stress-equivalent strain curve of the structure

将结构中单胞划分为A、B 2组如图4所示，其中A组单胞为与面板接触的单胞，B组单胞为中间3层单胞。

图4 矩形管划分示意Fig.4 Schematic diagram of rectangular tube division

根据图4可发现在该结构受到压缩载荷时，A组单胞与面板接触部分并未发生变形，但与B组单胞接触部分发生轻微弯曲变形，同时B组单胞中间部分上下面板发生大幅度弯曲变形，随着B组单胞上下表面的逐渐靠近拉动整体单胞呈现向内收缩变形，在2组单胞的共同作用下整体结构呈现向内收缩变形，表明该结构在压缩载荷下呈现负泊松比特性。

3 浮筏结构的振动性能分析

3.1 周期矩形管层数对浮筏结构振动特性的影响

为分析该结构中矩形管层数对该结构振动传递特性的影响，在矩形管壁厚为5 mm下，对5、9和13层进行振动分析。提取不同层数下该结构的前15阶固有频率和位移振级落差曲线如图5所示。

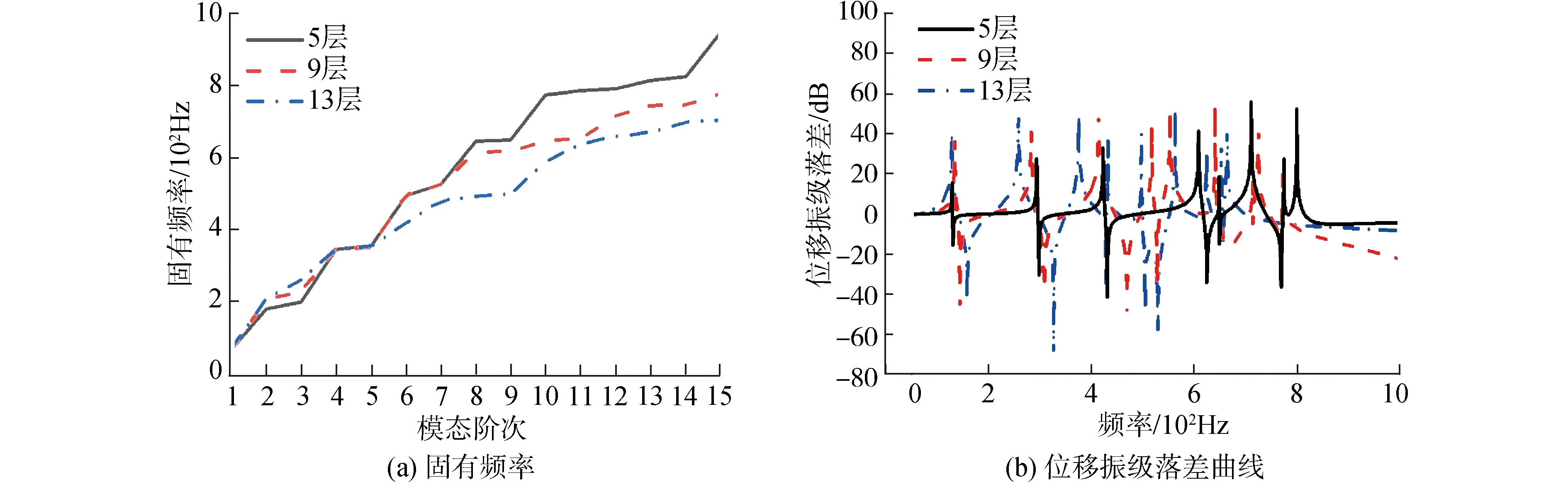
图5 不同层数下周期性矩形管浮筏结构Fig.5 Periodic rectangular tube floating raft structures with different story numbers

通过图5(a)可发现前4阶固有频率随着层数的增加逐渐增加，5～15阶固有频率随着层数的增加逐渐减少，相比5层而言，9层减幅17.45%，13层减幅25.11%。说明随着矩形管层数的增加，对整体结构的固有频率呈现先增大后减小的规律，可通过对层数的控制，实现对该结构固有频率的改变。根据图5(b)可发现在低频段，由于矩形管层数的增加该结构的刚度减小，使得该结构的位移振级落差幅值随层数的增加逐渐升高。同时在频率为327 Hz以及频率为502～536 Hz内，13层矩形管结构在0 db下的位移振级落差幅值较高同时有约30 Hz的隔振带隙，表现出较好的减振特性。说明矩形管层数的增加对于该结构的减振效果有一定程度的提升。

3.2 梯度周期矩形管对浮筏结构振动特性的影响

由于周期结构的变化对弹性波具有衰减特性，同时梯度排列的周期性矩形管结构同样会对弹性波传播过程中的阻抗造成影响，故为分析矩形管梯度壁厚对该结构振动传递特性的影响，固定矩形管层数为5层，对每层的壁厚(t)进行改变。为对比分析不同梯度排列的矩形管对整体结构的影响设置C1、C2、C3为对照组，即在面密度相同的情况下C1对应T1、T2，C2对应T3、T4，C3对应T5、T6，9组壁厚参数见表2。根据图6(a)可发现9组结构在15阶模态时固有频率在900 Hz内，故不考虑900 Hz以上的频率范围。提取9组模拟下的前15阶固有频率如图6(a)所示，并提取相同面密度下3组的位移振级落差曲线如图6(b)～(d)所示。

根据图6(a)可发现前5阶的固有频率基本重合，而6～15阶梯度排列的矩形管对固有频率有一定的影响。根据图6(b)可发现在0～400 Hz内C1T1T2基本重合，但在400～900 Hz内T1在0 dB以下的位移振级落差幅值逐渐升高，减震效果越来越明显。T2在580 Hz和745 Hz处出现2个吸收幅值，同时T1T2的隔振效果要优于C1。根据图6(c)可发现与C1组不同的是在0～400 Hz内T3T4便表现出较好的减振特性，在400 Hz之后T3在0 dB以下的位移振级落差幅值与C2相似，但在0 dB以下的位移振级落差幅值要优于C2，此外相比C2，T4整体的位移振级落差幅值都高于C2。说明T4对结构的振动响应具有放大和吸收的双重效应。根据图6(d)可发现在0 dB以上T5和T6的位移振级落差幅值要高于C3，但0 dB以下的位移振级落差幅值T5和T6与C3差别较小，在760 Hz～820 Hz内C3的减振效果要优于T5和T6。

表2 不同梯度排列的周期矩形管浮筏结构壁厚参数

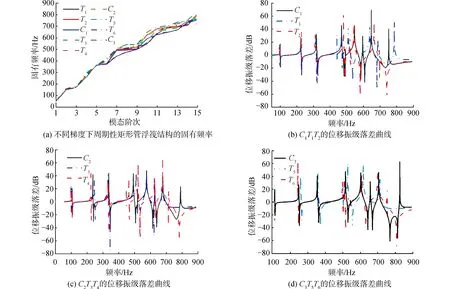
图6 不同梯度排列下周期性矩形管浮筏结构Fig.6 Periodic rectangular tube floating raft structure with different gradient arrangement

根据以上分析可发现，梯度排列的矩形管对结构固有频率的影响较小，但对整体减振效果有不同程度的提升，在不同面密度下梯度排列的矩形管结构表现出不同的减振特性。通过对矩形管的梯度设计可达到此结构在特定频率范围内的减振效果。

3.3 矩形管的壁厚对浮筏结构振动特性的影响

为分析该结构中矩形管壁厚对该结构振动传递特性的影响，在层数为9层下，对结构中矩形管的壁厚进行改变。提取7组不同壁厚下该结构的前15阶固有频率和位移振级落差如图7所示。

图7 不同壁厚下周期性矩形管浮筏结构Fig.7 Periodic rectangular tube floating raft structures with different wall thicknesses

根据图7(a)可发现随着矩形管单胞壁厚的增加，结构的固有频率逐渐升高，说明矩形管壁厚是影响结构刚度和固有频率最重要的参数之一。故调整矩形管单胞壁厚可以达到调控结构固有频率分布和提升减振效果的目的。根据固有频率的变化提取相对应的频率范围并分为图7(b)～(d)3个图进行分析，可以发现随着矩形管壁厚的增加位移振级落差峰值对应的共振频率分别为189.8、218.4、375.7、420.7、460.9和921.9 Hz，随着矩形管壁厚的增加结构的共振频率逐渐升高。

为更准确分析矩形管壁厚对该结构0 dB下位移振级落差幅值和减振带宽的影响，对图7中曲线进一步分析，以-20 dB为减振参考标准绘制柱状图(如图8所示)。

根据图8可发现随着矩形管单胞壁厚的增加，该结构0 dB下的位移振级落差幅值呈现先增大再减小最后增大的趋势。此外随矩形管单胞壁厚的增大，-20 dB下的频率带宽呈现先升高后减小的趋势。对于该结构而言，壁厚为4.5 mm和4 mm结构整体的减振效果优于其他壁厚。同时该结构的减振优劣和整体刚度并非线性关系，对于该结构而言，结构整体的减振效果随矩形管壁厚的增加，呈先增强后减弱。

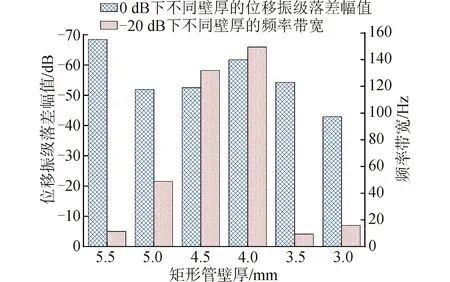
图8 不同壁厚下周期性矩形管浮筏结构的位移振级落差峰值和频率带宽Fig.8 Peak value of displacement vibration level drop and Frequency bandwidth of floating raft structure with periodic rectangular tubes of different wall thickness

4 结论

1)矩形管层数、矩形管排列方式和矩形管单胞壁厚对该结构的减振效果均有不同程度的影响，三者中矩形管单胞壁厚和矩形管层数对结构整体的固有模态影响较大。

2)梯度排列的矩形管对结构共振频率下的位移振级落差幅值和减振带宽影响较大。

3)对矩形管的层数、排列方式和单胞壁厚的改变可控制结构的减振频率、减振效果和减振带宽。