基于温度场逆问题的电力电缆缺陷检测方法研究

蒋益强， 方亚林， 赵文君， 杨永明， 刘行谋， 李 星

(1. 国网四川省电力公司宜宾供电公司， 四川 宜宾 644002； 2. 中国能源建设集团安徽省电力设计院有限公司， 安徽 合肥 230601； 3.输配电装备及系统安全与新技术国家重点实验(重庆大学)， 重庆 400044)

1 引言

随着电力电缆在输配电工业中的大量应用，其安全和稳定运行显得越发重要。在电缆的生产、安装和运行过程中，由于工艺缺陷、操作不当和环境影响等，难免使电缆内部产生缺陷[1]。缺陷严重的电缆在运行过程中的电场作用下，会恶化产生电树枝[2,3]、水树枝[4]，导致绝缘加速老化以至击穿[5]。针对电缆缺陷，一方面应当提高生产质量、规范化施工和运行；另一方面应当研究行之有效的缺陷诊断方法，及时发现和应对电缆缺陷，降低电缆故障造成的电力事故发生率。

电缆的内部缺陷难以通过直接的方式进行检测，目前比较有效的检测方法主要是通过定期预防性实验，例如tanδ检测法[6]、局部放电法[7]、直流漏电流检测法[8]等，测量表征电缆绝缘性能的电参数进行缺陷分析。传统的实验检测方法积累了大量数据，丰富了对缺陷的判断准则，但也存在一些弊端：大多数实验需要停电进行，降低了供电质量，并且过度实验往往会对电缆本身有一定“损伤”，加速绝缘老化。也有学者通过研究提出一些电缆故障的定位方法，如行波法[9]、阻抗法[10]等，能够在一定精度内定位电缆故障点，但对具体缺陷判断还存在一定困难。总之，针对电缆内部缺陷的检测，现有技术还存在一些局限，还亟需一些操作简便、准确可行的检测手段。

电力电缆在内部存在缺陷时，其热导率的分布势必与正常状态有所差异，从而导致运行中由电流热效应产生的电缆本体温度场分布变化。基于此，本文建立从电缆表面温度场分布逆推电缆内部热导率分布的逆问题模型，通过计算并对比电缆径向热导率分布图像，对电缆缺陷进行表征，实现电缆内部缺陷的检测。

2 电缆温度场逆问题建模与求解

2.1 温度场有限元算法

在建立电缆缺陷诊断的温度场逆问题模型之前，需要对已知电缆热导率分布和热激励条件下的温度场分布进行计算。

图1为电缆在电流负荷的焦耳热作用下达到稳态后会产生稳定温度场分布，不考虑电缆材料热参数在电缆轴向上的差异，可将电缆温度场计算简化为径向二维温度场分布计算问题。由固体传热学理论[11]可得电缆径向场域稳态温度场的控制方程为：

▽·[λ(x,y)▽T(x,y)]=-Φ(x,y)∈Ω

(1)

式中，λ为热导率分布，W·(m·K)-1；T为温度场分布，K；Φ为内热源功率体密度，W·m-3。

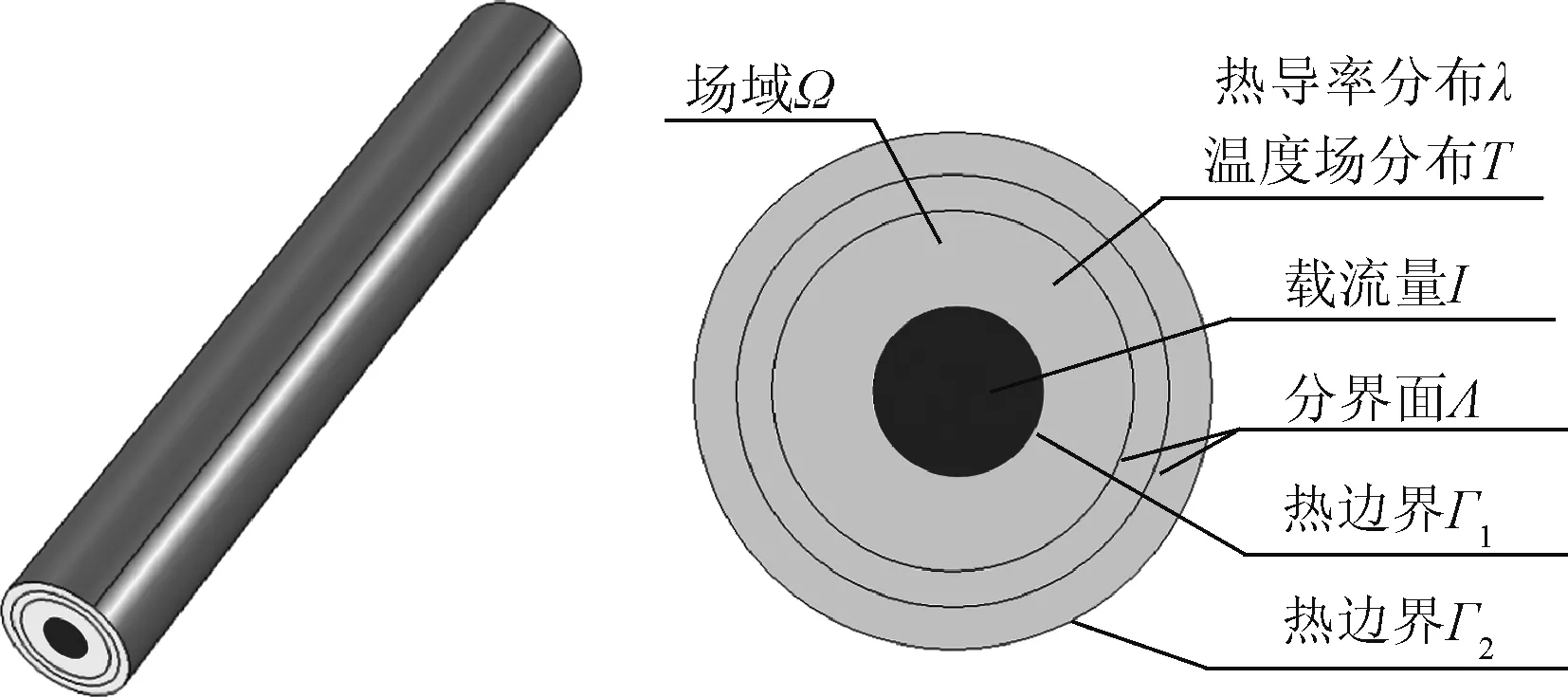
图1 电缆径向二维温度场模型Fig.1 2D radial temperature field model of cable

缆芯和电缆表面边界条件分别为第二类和第三类边界条件，即：

(2)

电缆内部不同介质层上的分界面衔接条件为：

(3)

式中，q为焦耳热的热通量，W·m-2；h为电缆表面与外界环境的对流系数，W·m-2·K-1；T1、T2、Tf分别为介质1、介质2中和环境的温度，K；λ1、λ2分别为介质1、介质2的热导率；n1、n2、n均为分界面的外法向单位向量。式(1)～式(3)即为电缆稳态温度场数学模型。

热通量q可通过电缆载流量I、缆芯周长l和缆芯单位长度有效电阻R[12]计算得到，即：

(4)

在工程问题中，对式(1)～式(4)一般采用数值算法求解，本文将采用有限元法[13,14]对电缆径向的温度场分布进行仿真和计算。

2.2 温度场逆问题模型

通过已知的电缆载流量和电缆各部分材料的热导率参数，可以通过求解传热学方程得到电缆的温度场分布，这一过程为温度场正问题计算。与之对应的温度场逆问题可以表述为：在已知温度场分布和载流量大小的情况下，对场域的热导率分布进行求解。电缆温度场正逆问题模型如图2所示。

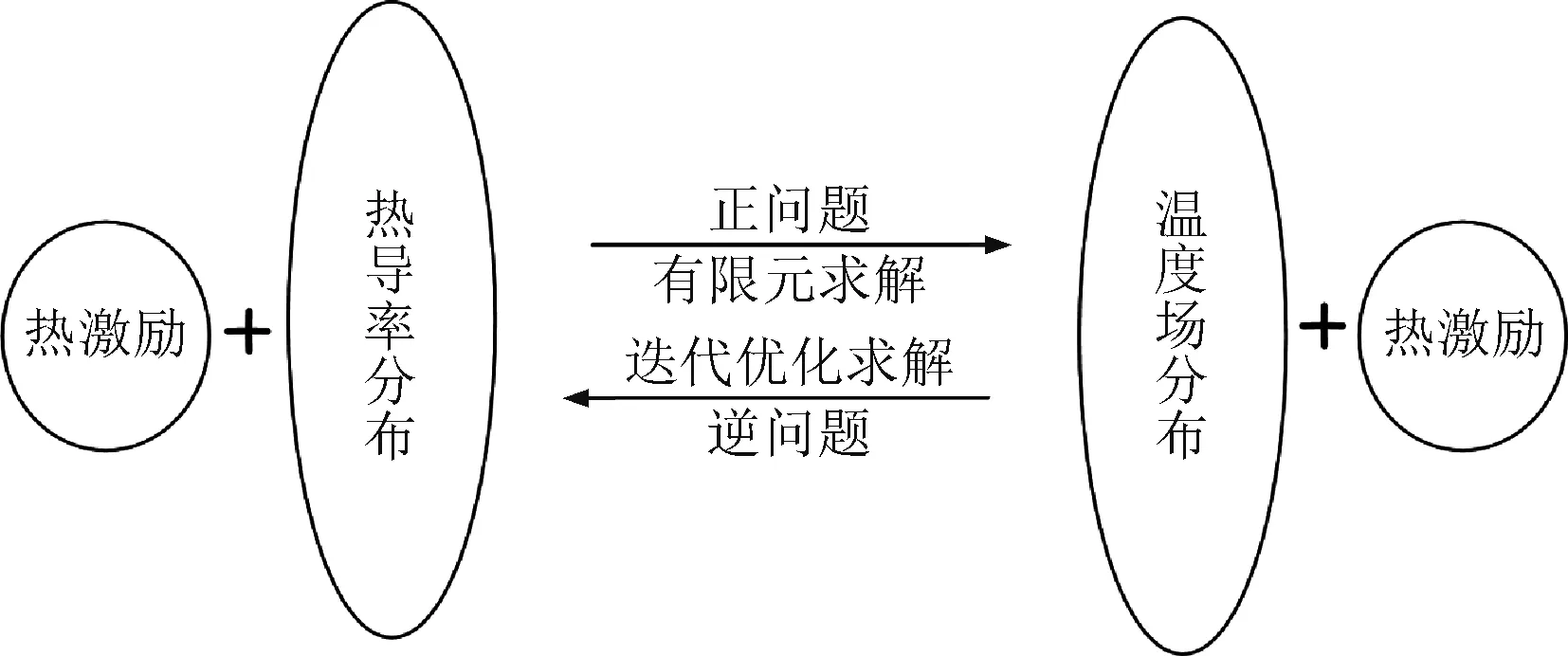
图2 温度场正逆问题模型Fig.2 Forward and inverse problem model of temperature field

在电缆的缺陷检测中，如果电缆内部存在局部严重老化、水树枝或其他缺陷，缺陷部分的热导率势必会与其处于正常状态下的热导率产生差异，从而导致缺陷状态和正常状态下的电缆温度场分布差异。因此，如果在实际中能够通过测量的温度场和载流量数据，反推出电缆的热导率分布，再与电缆正常状态的热导率分布进行对比，即可对电缆的缺陷状态进行检测。

在电缆径向温度场的正问题计算中，在载流量一定的情况下，只要给定一种电缆径向热导率分布，就可以通过正问题计算得到一种温度场分布。逆问题的模型建立即寻求一种热导率分布λ使正问题计算得到的温度场分布Tc与测量温度值T相等。实际中，这一关系难以精确满足，因此利用最小二乘法寻求最优解，建立温度场逆问题计算模型为：

(5)

式(5)是一个非线性优化问题，最优解为一阶微分驻点，在有限元模型中，即为：

(6)

为表述方便，用Fi(λ)表示误差函数E(λ)对λi的偏导数，即：

(7)

假设整个求解场域剖分为u个有限元单元，则逆问题求解共有u个同类的方程(式(7))，构成一组非线性方程组，即：

F(λ)=0

(8)

式中

(9)

运用牛顿迭代法[15]对式(9)进行求解，得到迭代公式：

(10)

式中，H为Hessen矩阵。

(11)

式(11)中忽略第二项高阶项后，得到：

H=JTJ

(12)

式中，J为表面温度值对有限元单元热导率的雅克比矩阵[16]。

2.3 逆问题模型求解

在进行逆问题的牛顿迭代法求解过程中，需要对Hessen矩阵进行求逆。实际电缆温度场的测量点只能布置在电缆表面，因此表面温度测量点n相对于场域剖分的单元数u非常有限，即n≪u，因此逆问题是一个欠定问题，由矩阵理论：

rank(H)=rank(JTJ)=rank(J)≤min{u,n}

(13)

式中，rank()为矩阵的秩；min{ }为取其中元素中的最小值。因此，Hu×u是一个非满秩矩阵，不能够直接进行求逆，使逆问题具有严重的病态性。为了克服矩阵的病态性，将对逆问题施加正则化提高求解的稳定性和准确性。

在病态问题的求解中，正则化方法通过增加罚项来对范数或者偏离初始值较大的解进行惩罚，对逆问题模型施加典型的Tikhonov正则化[17]，有：

minE(λ)=‖Tc(λ)-T‖2+α‖L(λ-λ(0))‖2

(14)

式中，α为正则化参数；L为正则化矩阵(Tikhonov正则化中取单位阵)；λ(0)为热导率初始值。

再对施加正则化后的逆问题运用牛顿迭代法求解式(14)得到：

(15)

式(15)的迭代结果即为电缆缺陷检测温度场逆问题模型的解。电缆温度场逆问题的整个求解流程如图3所示。

图3 电缆温度场逆问题求解流程图Fig.3 Flow chart to solve inverse problem of power cable temperature field

3 仿真实验分析

3.1 电缆温度场仿真分析

从传热学角度看，电力电缆在缺陷状态下，其热导率分布会与正常状态有所差异，从而导致温度场的分布差异，这为电缆的缺陷检测提供了契机。电缆水树枝缺陷在电缆运用中时常发生，水树枝的存在会使其周围绝缘材料在电场作用下加速老化，热导率会有所增大。本节将对电缆典型水树枝缺陷下的温度场分布和基于温度场逆问题计算的缺陷检测进行仿真实验分析，其他缺陷状态分析与之类似。

以YJLW 64/110 kV单芯电缆[18]为例进行仿真分析，由于电缆的铠装和屏蔽层热导率较大，几何厚度较薄，热阻小，对温度场分布影响较小，因此在物理建模中，进行了忽略简化。电缆水树枝形态呈不规则树枝状，在仿真模型中通过不规则细长的椭圆来模拟水树枝及其周围老化的绝缘材料，并设定为水的热学参数。通过查阅电力电缆手册和相关材料的物性参数，得到仿真模型的相关参数见表1。

表1 YJLW 64/110 kV电缆仿真模型参数Tab.1 Simulation model parameters of YJLW 64/110 kV cable

在温度场仿真计算中，分别对电缆绝缘层含有单个和多个水树枝缺陷下的电缆表面温度场进行了计算，其三角形有限元模型剖分规模含有单元数和节点数均在104数量级(例如含有单个缺陷的模型三角形剖分包含10 394个单元、5 278个节点)，仿真模型坐标原点设在电缆中心，例如正常状态电缆的仿真模型和有限元剖分模型如图4所示。仿真模型中，设环境温度303.15 K(27 ℃)，空气自然对流系数h= 5 W·m-2·K-1(在自然无强制对流环境下，一般为3～10 W·m-2·K-1)，电缆在载流量1 000 A下，温度场到达稳定状态的仿真结果如图5所示。

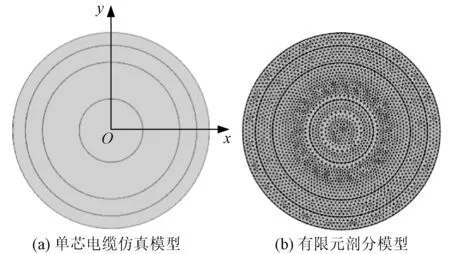
图4 单芯电缆仿真模型与剖分模型Fig.4 Simulation and FEM mesh models of single core cable

从温度场的仿真结果看出，正常状态下，电缆表面温度场均匀分布(图5中近似水平直线)，数据近似为定值，约为318.27 K。当电缆在内部存在水树枝典型缺陷时，电缆温度场分布发生畸变，电缆表面温度与正常电缆有明显差异，在缺陷附近的表面温度较高，表面温度分布的最高最低温度差达2 K左右。明显的温度分布差异可以为逆问题缺陷检测提供足够的数值精度。

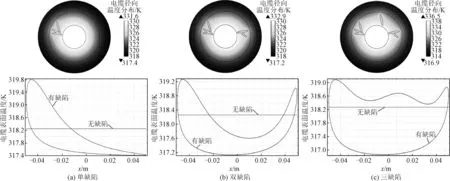
图5 电缆径向温度场及电缆表面温度分布Fig.5 Radial temperature field and surface temperature distribution of cable

3.2 电缆缺陷检测仿真分析

基于3.1节中的仿真结果，将电缆表面的温度数据代入温度场逆问题模型，通过迭代求解得到电缆径向的热导率分布如图6所示。

图6 电缆径向热导率分布Fig.6 Radial thermal conductivity distribution of cable

对比逆问题计算得到的电缆热导率分布，当电缆绝缘层中存在典型水树枝缺陷时，热导率分布图像中会呈现高于周围正常绝缘层热导率的局部高热导率区域(图6中黑色虚线圈内)，表明此处存在局部缺陷，通过对比无缺陷状态下的热导率分布图像，可大致判断缺陷的位置和大小。随着缺陷的增多，逆问题计算得到的热阻率图像分辨率有所下降，但其分辨率仍能够对缺陷进行判断。在实际中，存在多处缺陷的电缆一般较少，因此该方法能够满足对电缆的缺陷检测需求。

通过仿真分析验证了当电缆内部存在局部缺陷时，会导致电缆温度场分布的畸变，通过电缆表面温度场数据建立的逆问题模型能够实现电缆内部缺陷的有效检测。

图7 电缆缺陷检测模拟实验平台Fig.7 Setup of defect detection on simulated cable

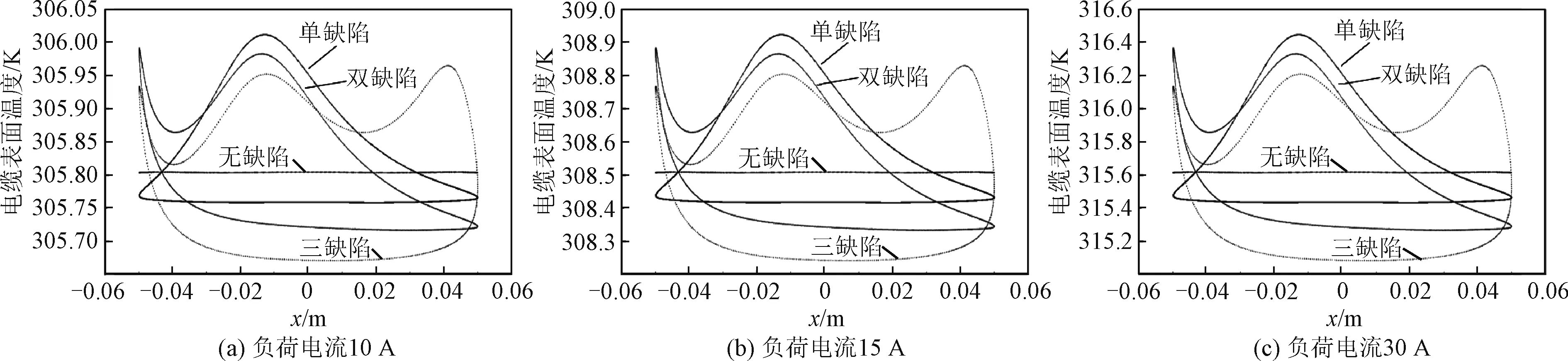
图8 不同负荷电流下模拟电缆的表面温度分布Fig.8 Temperature distribution of simulated cable under different load current

4 模拟实验分析

为验证通过温度场逆问题计算进行电缆缺陷检测方法的准确性和可行性，在实验室搭建了模拟电缆实验平台。实验中，利用石墨棒模拟电缆导体，填充硅胶作为绝缘材料，使用恒流源为模拟电缆提供负荷，同时采用FLIR SC7000红外热像仪(热灵敏度< 0.025 K)对电缆表面温度数据进行采集。实验模型中的石墨导体和填充硅胶具有与实际电缆的铜芯导体和绝缘层材料局域非常近似的热特性参数，且几何尺寸类似，在相关研究中已证明该“石墨-硅胶”模型能够对实际电缆的热特性分布进行良好模拟[19]。

为了模拟电缆局部缺陷和激励电流大小对缺陷检测结果的影响，在绝缘层中预植单个、两个和三个椭球形水树枝缺陷，并分别提供负荷电流10 A、15 A和30 A进行对照实验，整个模拟实验平台与模拟电缆结构如图7所示。

实验中，测得环境温度约20 ℃，分别设置恒流源电流为10 A、15 A和30 A给模拟电缆提供负荷，并分别对正常段和预植缺陷段的电缆表面温度进行了数据采集，当电缆表面温度达到稳定后，测得温度数据如图8所示。

从采集的实验室模拟电缆表面温度数据看出，在电缆内部存在缺陷时，温度场分布发生畸变。不同负荷电流激励下的温度场分布曲线特点类似，但数值大小有所差异，这是由于仅仅改变了热激励大小，而其他热参数保持不变。当负荷电流越大时，电缆表面的温度值也越高，为逆问题求解提供的数据数值精度也越高。

将上述采集到的温度数据导入温度场逆问题检测程序进行缺陷诊断计算得到的电缆热导率分布图像如图9所示。

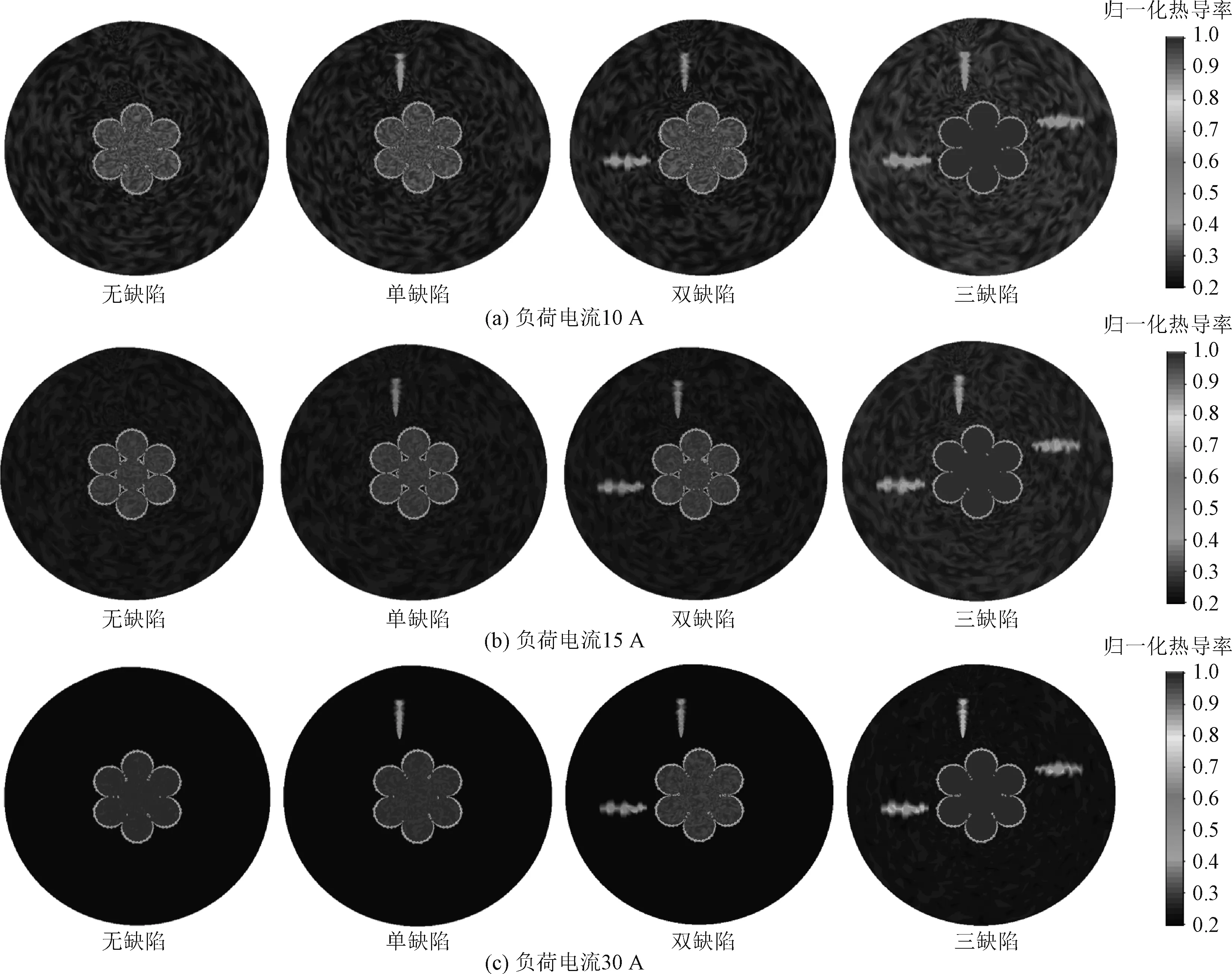
图9 实验室模拟电缆缺陷检测结果Fig.9 Defect detection results of simulated cable in laboratory

从模拟实验温度场逆问题计算得到的电缆热导率分布结果看出，通过对比无缺陷段和预植缺陷段的电缆径向热导率分布图像，可以明显发现热导率图像的异常，从而判断局部缺陷的大致范围和缺陷类型。对比分析不同负荷电流条件下的热导率分布图像可以看出，当负荷电流较大时，热导率图像各部分的对比度更高，能够更加清晰地判断缺陷的大小和位置，因此在实际条件允许的情况下，应当尽量增大负荷电流以提高图像的分辨率，从而提高检测的准确度。

5 结论

电力电缆在局部缺陷状态下运行，其温度场分布会与正常状态的电缆有所差异，本文通过提取电缆表面温度场的差异信息，建立温度场逆问题模型计算电缆的热导率分布，进而反映电缆缺陷状态。仿真和模拟实验结果表明，电缆径向温度场逆问题模型能够有效判断电缆内部局部缺陷的大致范围和大小，实现电缆缺陷检测。该方法无侵入、无需大型实验，作为一种新兴技术将对现有检测方法进行有力补充。