一种适用于直流微电网的自适应动态下垂控制策略
2022-10-09段梦珂汤茂东曲小慧
徐 鹏, 段梦珂, 潘 艳, 汤茂东, 曲小慧, 董 烨
(1. 国家电网公司华北分部, 北京 100053; 2. 南京南瑞继保电气有限公司, 江苏 南京 211102; 3. 东南大学电气工程学院, 江苏 南京 210096)
1 引言
分布式可再生能源的发展和直流负荷的增加使得直流微电网得到大力推广和使用[1-4]。为提高直流微电网的容量和可靠性,可再生能源多通过并联方式连接到直流母线中。考虑并联电源的功率定额,需实现负荷功率的合理分配,下垂控制是目前常用的控制方法[5]。由于线路中存在不可避免的阻抗,传统的下垂控制存在母线电压调整率和电流分配精度互相矛盾的问题[6-10]。
为缓解二者之间的矛盾,文献[11-14]提出一系列非线性下垂控制策略,通过在不同的负载条件下设置不同的下垂系数,轻载时采用较小下垂系数,重载时采用较大的下垂系数,在保证一定负荷电流分配精度的前提下,尽量减少直流母线电压的跌落。为了进一步补偿母线电压偏差,文献[14]在下垂控制策略中增加电压修正参数,通过反馈各电源的电流来调整修正系数,从而调整输出电压基准。文献[15,16]则采用多模式控制,下垂系数的设计需考虑系统的运行模态,从而减少电压偏差。以上方式虽然在一定程度上缓解了电压跌落和负荷分配精度的矛盾,但下垂系数在一定的负载条件或运行状态下是固定的。当系统工况变化或者线路阻抗变化时,无法确保母线电压和功率分配准确度均在可接受的范围内。
文献[17-20]采用增加上层通信的方式,实时反馈母线电压到下层变换器控制端口,调整变换器输出基准,保证母线电压不低于最低标准值,稳定母线电压。但该控制依赖上层集中式通信,可靠性差。因此,文献[21,22]提出采用离散一致性算法,避免上层集中式通信,通过本地通信交换相邻变换器的电压或电流信息,针对负载分配精度与母线电压调整率两个目标进行算法迭代,得到目标下垂系数,从而进行自适应的下垂控制。然而,离散一致性算法需采样本地多个节点信息,两个目标函数的迭代过程长、计算复杂、占用资源多。此外,传感器等电气元件引起的测量和计算误差也会影响下垂控制的精度和稳定性。
为了解决以上问题,本文提出了一种简单的自适应动态下垂控制方法,可通过反馈相邻变换器的电流信息进行一增一减迭代逼近,快速地动态调整负载电流,实现所需的负荷电流调整度。由于目标下垂系数介于线路阻抗之间,不会增加母线电压下跌,保证母线电压调整率在可接受的范围内。该方法不需要二次控制,不需要上层集中式通信,只需通过本地通信交换相邻变换器信息,可靠性高。最后,本文以两台并联DC-DC变换器为例进行仿真验证,在给定负荷电流均流精度为2.5%、电压调整率为5%的前提下,通过该算法可快速实现宽负载范围内的电流均流和母线电压稳定,仿真结果验证了理论分析的正确性。
2 直流微电网中的下垂控制思路
在直流微电网中,并联电源与直流母线间的线路阻抗不同会导致负载分配不平衡。为简化分析,此处以两个并联的直流变换器为例,如图1所示,分析下垂控制对其输出电流和母线电压的影响。其中,Ubus和Io分别为直流母线电压和负载电流,R1和R2为两个变换器与直流母线间的线路电阻,RL为负载电阻,Uo1、Uo2和I1、I2分别为两个变换器的输出电压和输出电流,设其母线额定输出电压均为UN。Rd1和Rd2为两个变换器构建的虚拟电阻,亦称为下垂系数。
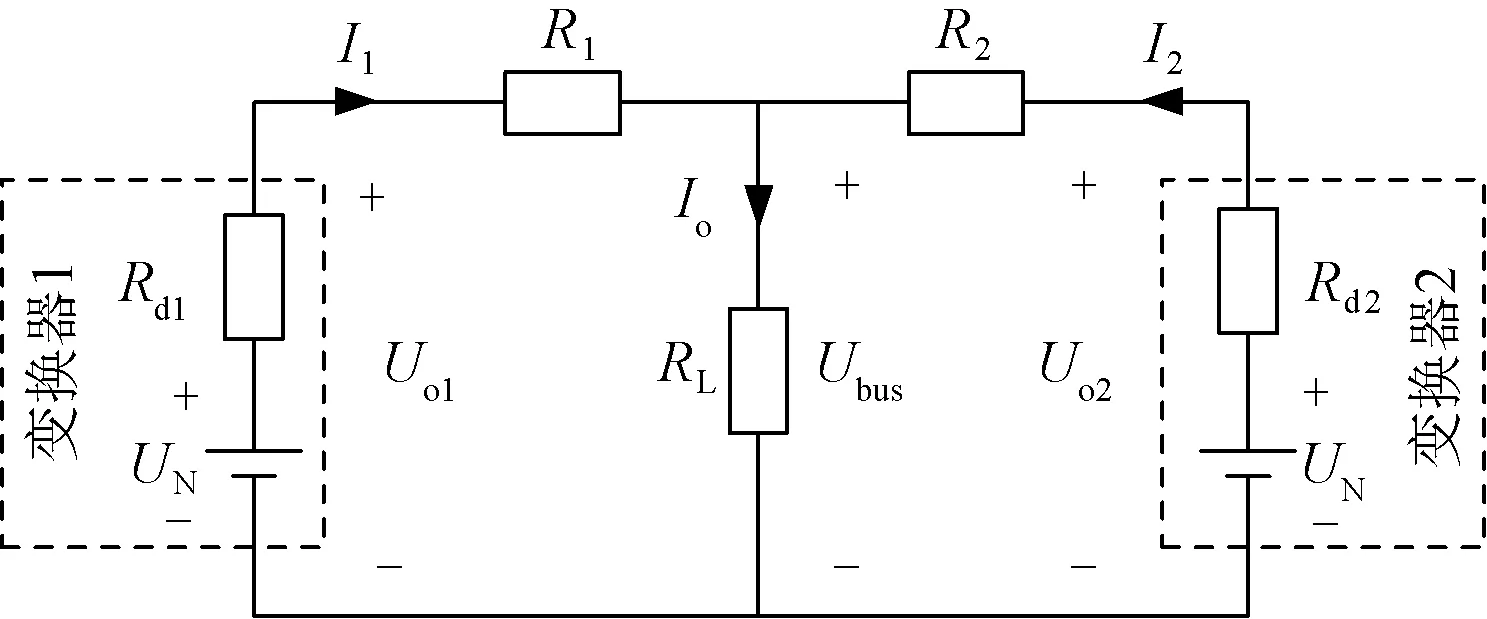
图1 采用两个并联直流变换器的简化直流微电网Fig.1 Simplified DC microgrid with two parallel-connected DC-DC converters
传统线性下垂系数控制表示为:
(1)
式中,Umin为母线电压允许的最小电压值;Iimax为变换器输出电流Ii的最大值。
那么,变换器的输出电压基准Uo(ref)i应表示为:
Uo(ref)i=UN-IiRdi
(2)
将式(2)的下垂控制表达式应用到直流变换器的电压控制环中,就可得到两个变换器的电压跌落不小于Umin,此时两个变换器的输出电流满足。
(3)
由此可见,如果线路阻抗远小于下垂电阻,电流的分配精度主要依靠下垂电阻。
定义标幺化的电流偏差eI和电压偏差eU分别为:
(4)
(5)
式中,Iomax为负载电流最大值。
对图1电路运用基尔霍夫电压定律(KVL),即:
Ubus=UN-IiRi-IiRdi
(6)
画出变换器外部输出特性,如图2所示。图2中实线表示采用传统线性下垂的母线电压Ubus随变换器电流I1和I2的变化曲线。当负载电流Io不变时,随着实线的下垂电阻增大,电流偏差ΔI随之变为更小的电流偏差ΔI′,但电压偏差则从较小的ΔU变为较大的ΔU′。如果电压跌落至Umin以下,此时尽管ΔI′较小,但下垂电阻不可接受,需调小其虚拟电阻阻值。但电阻调小,又不能保证电流偏差满足要求,这也是传统下垂控制的矛盾。
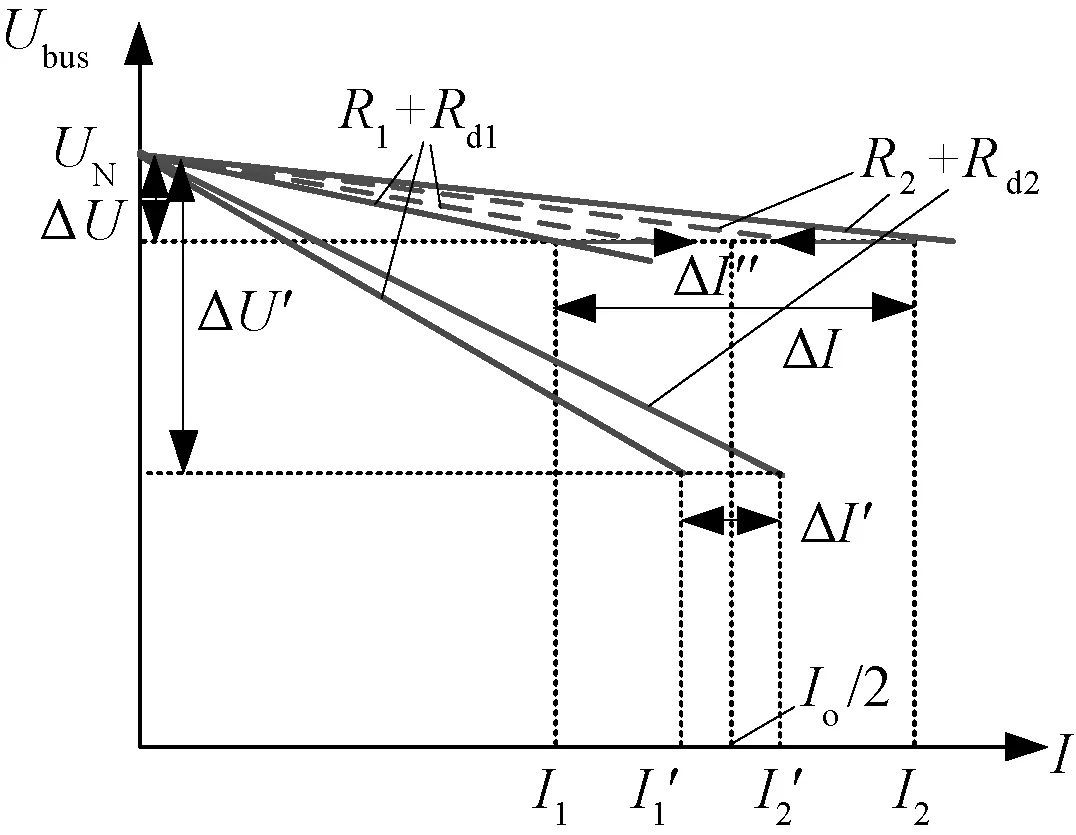
图2 变换器外部特性曲线Fig.2 External characteristics of converters
为避免这个矛盾,如果两条曲线采用一增一减逼近,如图2中虚线所示,两条曲线在相同的ΔU下,可实现较小的ΔI″,直到电流偏差达到eI要求。此时一增一减逼近中的减是增加了一个负斜率Rd1,因为R1和R2线路阻抗相对较小且难以测量,若Rd1绝对值大于R1,外特性曲线R1+Rd1会出现上翘,将导致两条曲线的电流偏差ΔI越来越大,系统易不稳定。因此本文提出一种新的动态逼近调整方法,自适应迭代生成下垂系数,使其外特性曲线斜率永远为正。具体实现方法将在第3节介绍。
3 所提自适应动态下垂控制方法
由第2节的分析可知,采用传统的下垂控制难以同时满足高负荷分配精度与低电压调整率。若能一增一减逼近,如图2虚线所示,可以同时满足所需的电压调整率和电流分配精度。
当线路阻抗无法直接测量,并在给定的eI和eU的前提下,图2中一正一负的下垂系数获取至关重要。因此,本文提出了一种基于相邻通信的自适应动态下垂控制方法,该方法只需检测本地变换器输出电压与输出电流信息,不需要全网通信,根据算法迭代,求出动态下垂系数,即可实现所需的电压调整率和电流分配精度。
具体实现方法如下:
步骤1:首先,根据反馈本地变换器的输出电压Uo1和Uo2以及电流I1和I2,通式(4)和式(5),判断eI和eU是否满足设计要求。如果满足要求,则不需要下垂控制。如果不满足设计要求,根据式(7)对线路阻抗进行预估,得到线路阻抗R1和R2。
(7)
步骤2:如果线路阻抗准确,那么根据图2,理论的下垂阻抗分别为:
(8)
那么两条曲线完全重合,电流偏差为0。但由于线路阻抗无法准确获得,根据式(7)的预估,必然会存在一定偏差。按式(8)的下垂系数进行控制,得到新的输出电流和电压。若此时eI和eU满足设计要求,那么,此下垂系数即为设计值。若不满足要求,则需下一步进行迭代。
(9)
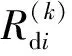
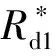
依然以两变换器并网为例,算法逻辑如图3所示,将此算法嵌入到本地控制器中,即可得到该系统的控制逻辑图,如图4所示。
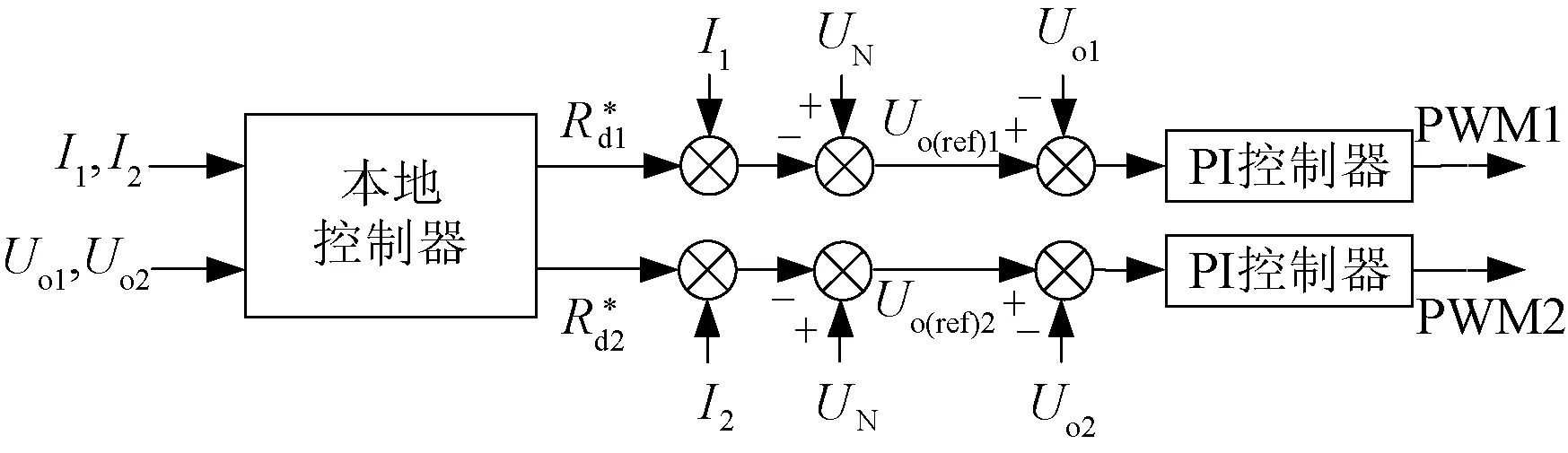
图3 采用自适应下垂控制的两变换器控制框图Fig.3 Control diagram of two converters with proposed adaptive droop control
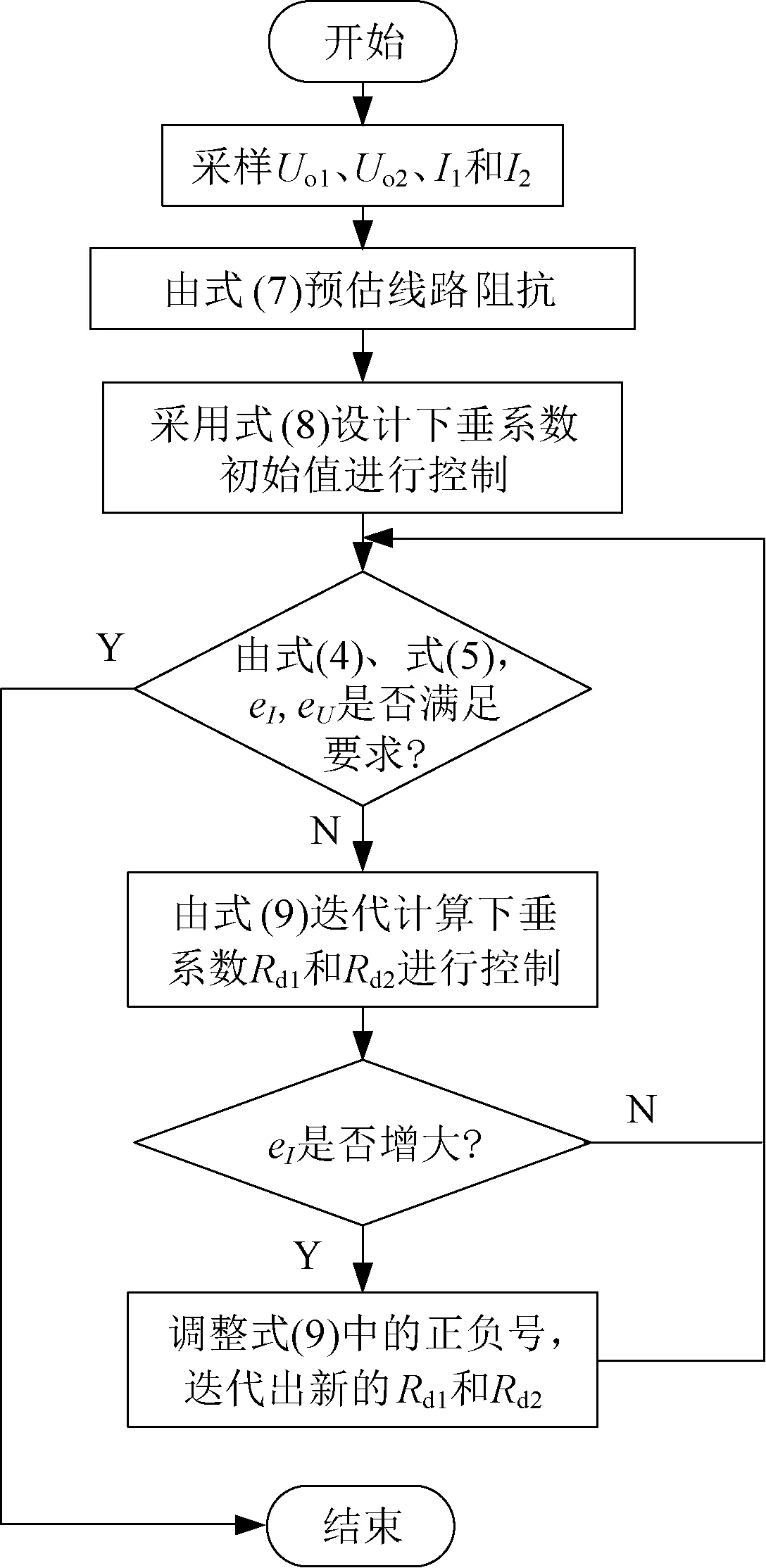
图4 自适应下垂控制流程图Fig.4 Flow chart of adaptive dynamic droop control
根据图3,在不同的负载条件下,可实现变换器1和变换器2输出电流和输出电压满足给定电流偏差精度和电压调整率。现以两个变换器并联为例,母线电压为48 V,两个变换器最大输出电流I1max、I2max均为2 A。目标电流偏差eI≤2.5%,电压偏差eU≤ 5%。根据图4的迭代流程,可得到不同负载条件下的母线电压Ubus随变换器输出电流的变化曲线,如图5所示。
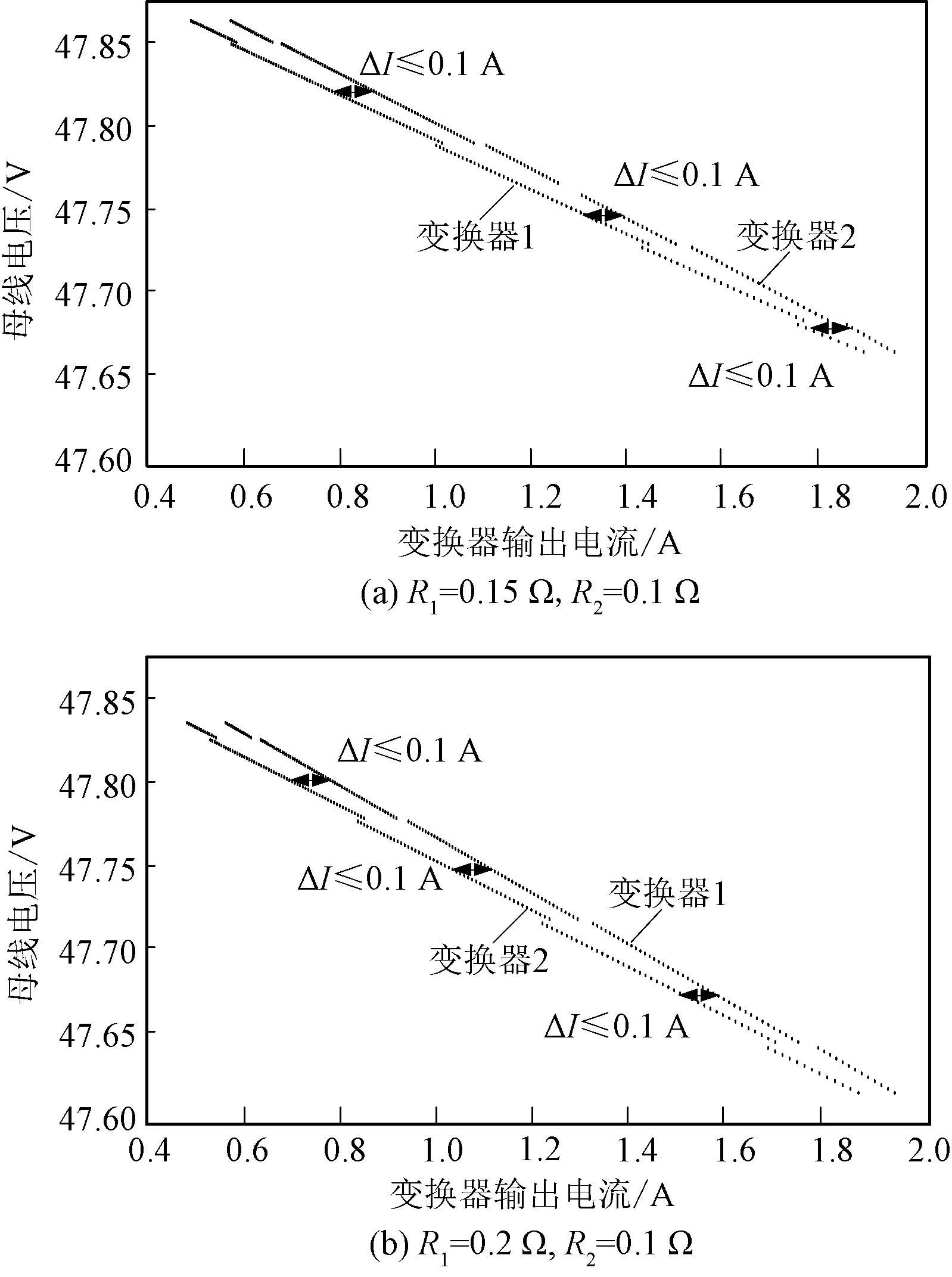
图5 变换器母线电压随输出电流变化曲线Fig.5 Bus voltage varying with converter currents

4 仿真结果及分析
为了验证上述分析,利用Matlab建立了两个DC-DC变换器系统的仿真模型。由于两个变换器输入电压低于母线电压,所以采用Boost变换器。仿真模型的参数见表1。为了更好地体现效果,仿真结果给出了采用传统下垂控制和本文所提出的自适应动态下垂控制两种情况做比较。
4.1 传统下垂控制
若变换器采用传统下垂控制,下垂系数的选择对系统的输出性能影响很大。图6给出了下垂系数Rd1=Rd2=0.1 Ω时的系统母线电压和两个变换器输出电流波形。负载初始为半载,即RL=24 Ω,此时母线电压从图6(a)可见,由于下垂系数小,负载电流小,电压跌落较小,为47.8 V。但此时两个变换器输出电流偏差ΔI相对较大,为0.24 A,eI为6%已超过规定的2.5%。2.0 s时,负载由半载增加到满载,如图6(b)所示。母线电压由于重载条件,母线电压跌落至47.6 V,但仍然远远满足eU≤5%的要求。但此时电流偏差进一步增加至0.57 A。因此,当下垂系数很小时,传统的下垂控制难以满足负荷分配精度,与理论分析一致。

表1 仿真参数Tab.1 Simulation parameters
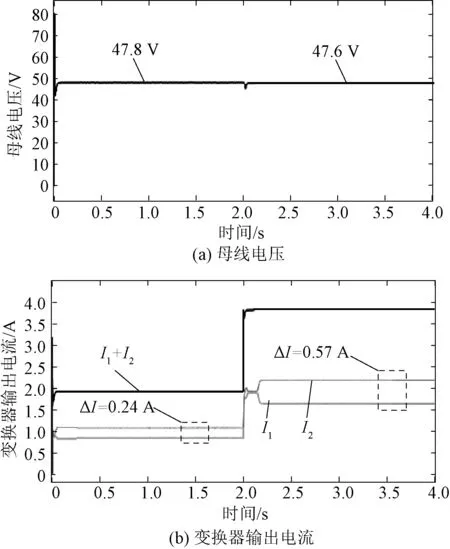
图6 采用传统下垂控制Rd1、Rd2=0.1 Ω时的仿真波形Fig.6 Simulation waveforms with droop resistance of Rd1,Rd2= 0.1 Ω
为了减少负载电流偏差,图7给出采用较大的下垂系数,即Rd1=Rd2=1 Ω时的母线电压和变换器输出电流波形。同样地,变换器先工作在半载条件下,此时的负载电流偏差大大降低,仅为0.06 A,eI为1.5%。但此时母线电压由于大的下垂系数,跌落至46.9 V,eU约为2.3%,仍未超过5%的限值。
当负载切换至满载时,母线电压进一步跌落至45.5 V,此时eU为5.2%,已超过5%的限值,同时,由于负载增大,电流偏差也随之增加至0.13 A,此时的eI为3.25%已超过规定的2.5%。因此,为保证电流分配精度满足要求,需采用更大的下垂系数。但不可避免带来电压跌落的进一步增加,难以满足母线电压调整率的要求。
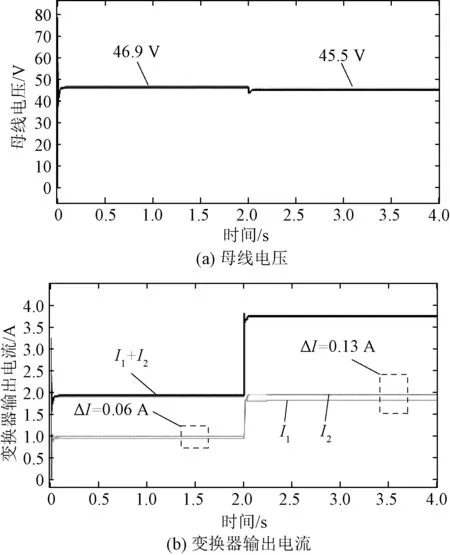
图7 采用传统下垂控制Rd1、Rd2=1 Ω时仿真波形Fig.7 Simulation waveforms with droop resistance of Rd1,Rd2=1 Ω
4.2 自适应动态下垂控制
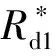
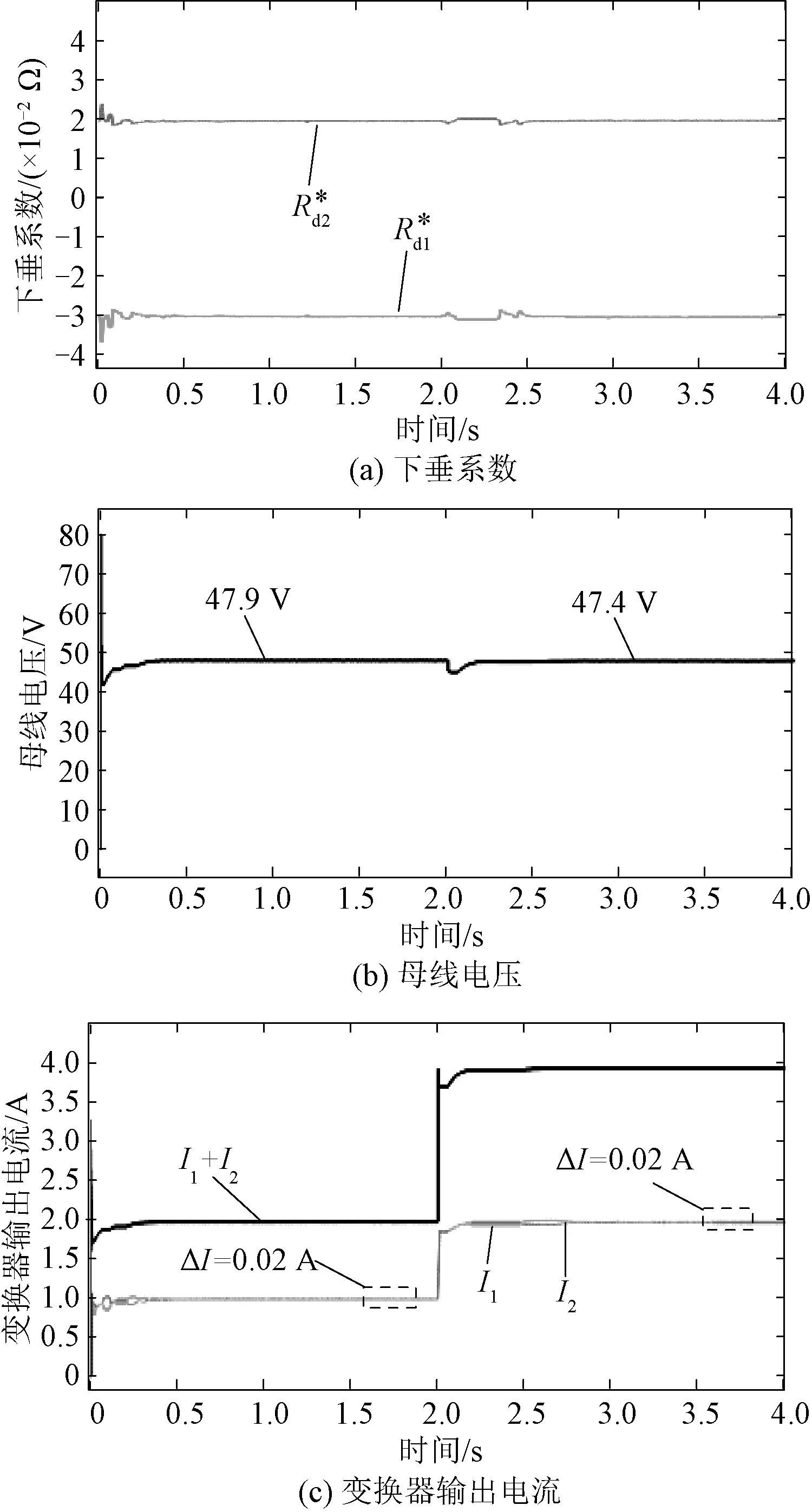
图8 采用自适应动态下垂控制时的仿真波形Fig.8 Simulation waveforms with proposed adaptive droop control scheme
将图8(a)的下垂系数代入图4的变换器控制中,可得到如图8(b)、图8 (c)所示的母线电压和变换器输出电流波形。由于动态下垂系数可以自适应负载的变化,半载和满载时的输出电流偏差几乎不变,约为0.02 A,eI为0.5%远小于规定的2.5%。由于动态下垂系数小,其母线电压则分别为47.9 V和47.4 V,亦远小于规定的5%偏差范围。因此,本文所提的自适应动态下垂控制可以在宽负载范围内快速实现高电流分配精度和低母线电压调节率。
5 实验结果与分析
为进一步验证上述理论和仿真分析,搭建了如图9所示的两组Boost变换器输出并联实验平台,实验参数见表2。

图9 两个变换器并联的实验平台Fig.9 Experimental platform with two parallel-connected converters
图10和图11为加入所提下垂控制策略前后对比波形,负载由120 W跳变到200 W。无下垂控制时,母线电压由47.8 V跳变到46.2 V,变换器输出电流由1.55 A、0.98 A跳变到2.55 A、1.7 A,最大电压偏差和最大电流偏差分别为3.75%和28.3%。加入所提控制策略后,母线电压由48.2 V跳变到约47.9 V,变换器输出电流由1.31 A、1.28 A跳变到约2.2 A、2.15 A,最大电压偏差和最大电流偏差分别为约0.4%和1%。可以看到,所提下垂控制可以自适应调节下垂系数以保证电压偏差和电流偏差始终保持在规定范围内,符合上述仿真及理论分析,亦验证了本文所提下垂控制可以在较宽负载范围内满足电流分配精度和母线电压调节率要求。

表2 实验参数Tab.2 Experimental parameters
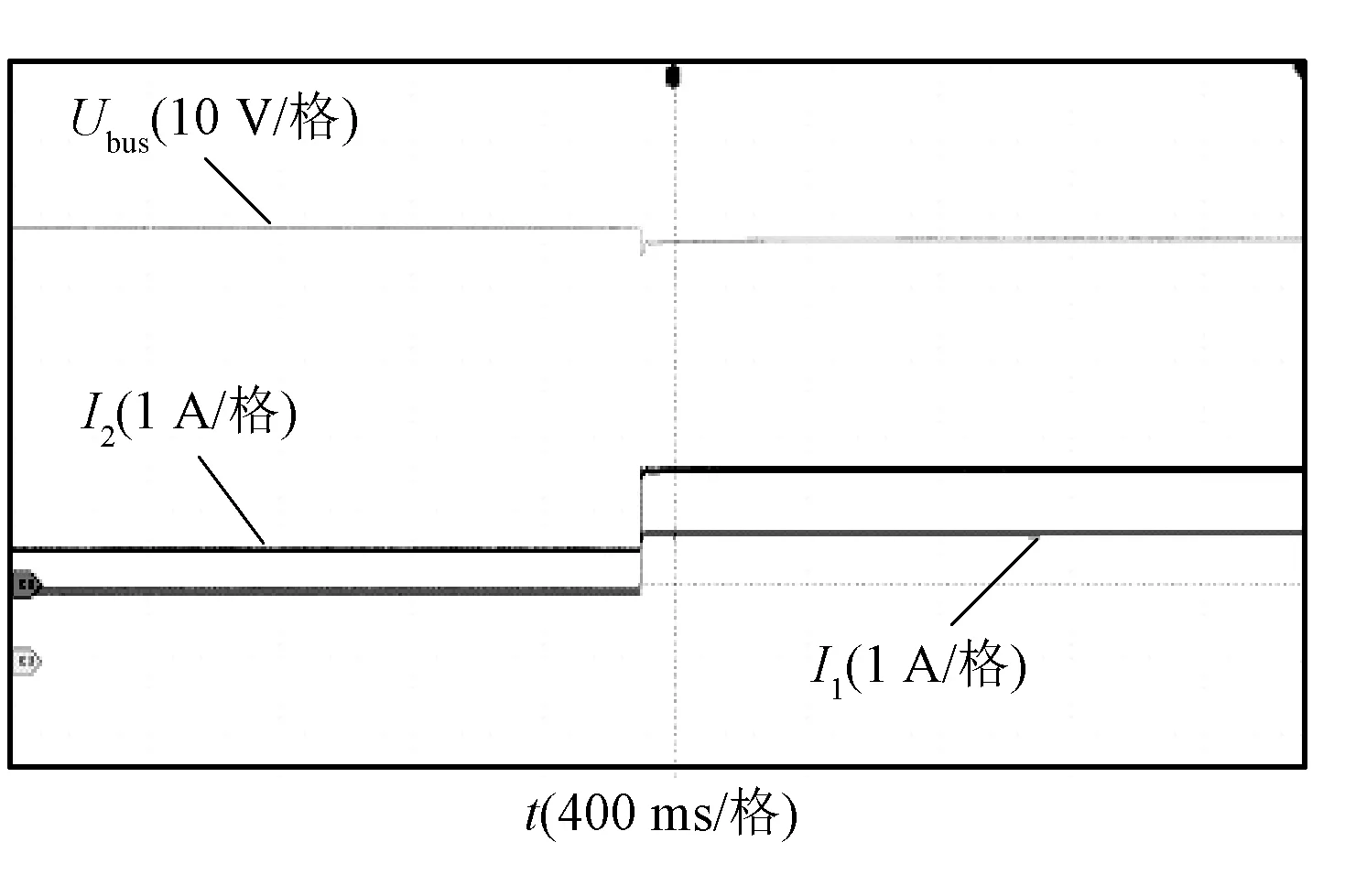
图10 无下垂控制时母线电压和变换器输出电流Fig.10 Bus voltage and converters output current without droop control
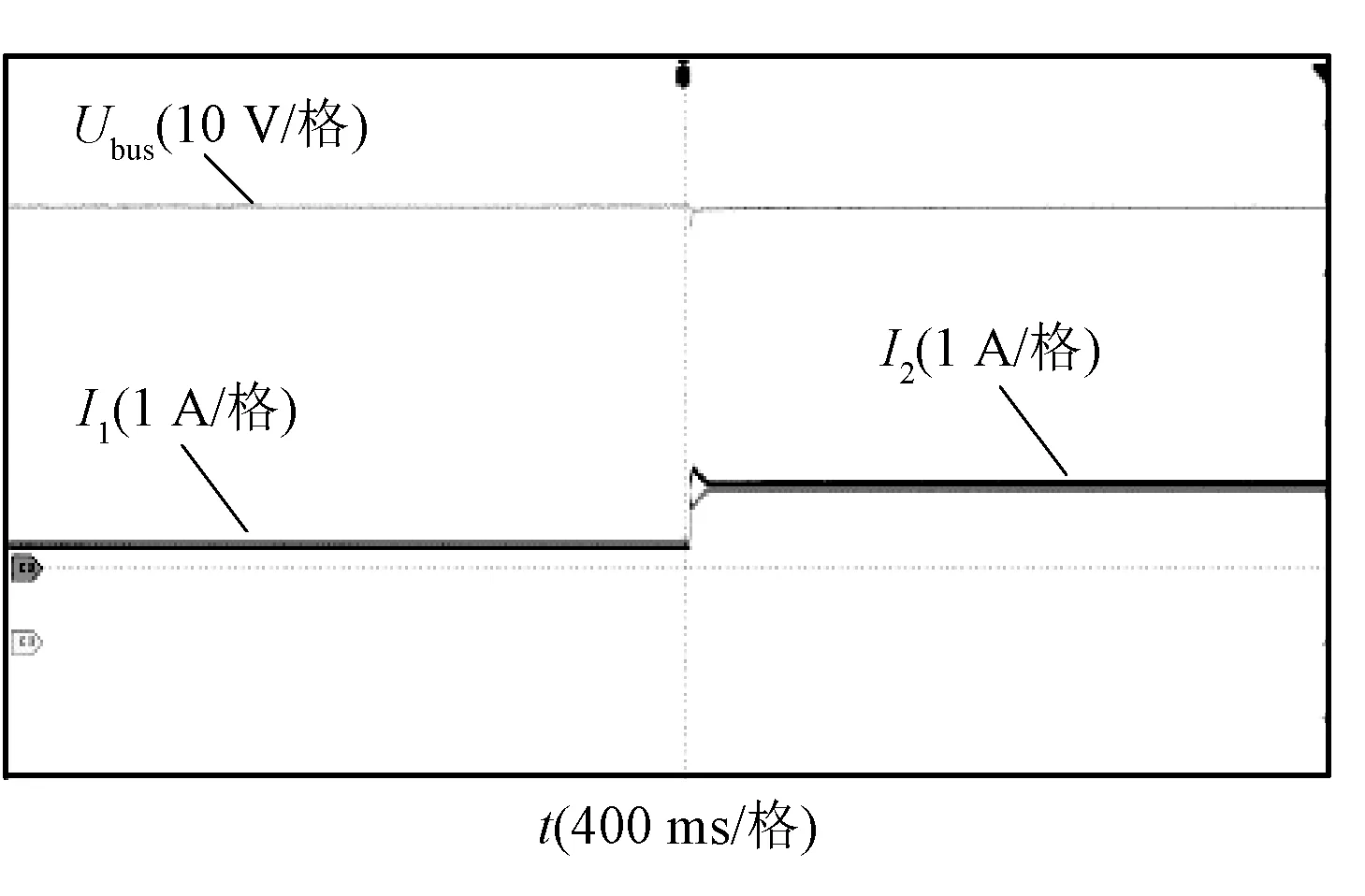
图11 自适应下垂控制下母线电压和变换器输出电流Fig.11 Bus voltage and converters output current with proposed adaptive droop control
6 结论
本文针对传统下垂控制不能同时实现高电流分配精度和低母线电压调节率的问题,提出了一种基于简单迭代方程的自适应动态下垂控制方法。该方法通过本地变换器相邻通信,在正负之间微调下垂系数,快速实现所需的负荷电流调整度,且不会造成母线电压的进一步下跌,保证母线电压调整率在可接受的范围内。该方法只需通过本地通信交换相邻变换器信息、可靠性高。最后,仿真与实验结果验证了本文所提算法的有效性。
