输出与变压器参数完全解耦的S/SP补偿IPT系统的最优增益点研究
2022-10-09白瑞昕
侯 佳, 白瑞昕
(南京邮电大学电子与光学工程学院、 柔性电子(未来技术)学院, 江苏 南京 210023)
1 引言
无线电能传输(Wireless Power Transfer, WPT)技术因其能够提供物理和电气层面的双重隔离,在家用电器[1]、医疗[2]、电动汽车[3]、水下勘探[4]、矿井油田等诸多供电场合有着传统的金属-导体接触式电能传输方式不可比拟的优势[5-7]。近年来,WPT技术及其应用呈现井喷式发展,据IHS Markit预计到2022年搭载WPT充电技术的设备将达到20亿台[8]。其中,基于电磁感应原理的感应式无线电能传输技术(Inductive Power Transfer, IPT)因其系统效率高、传输功率大,目前应用最为广泛[9]。
IPT系统中相互分离的磁耦合线圈在非接触变压器中产生了相当大的漏感,降低了系统的功率传输能力、影响到系统的输出稳定性[10]。为对大漏感进行补偿,通常采用谐振补偿技术,以在变负载下获得稳定的输出、伴有单位功率因数以提高功率传输能力[11-14]。
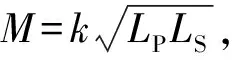
一些高阶的补偿网络如LCL补偿[16]、LCC补偿[17]、单边T或Π型补偿[18]可提供更大的设计自由度,令输出不依赖于变压器参数。但这些补偿网络中的外加磁性补偿元件会带来较大的铜损和铁损,同时也增加了电路成本与体积重量。文献[19]研究了仅采用容性补偿元件的S/SP补偿网络,并指出通过调节原、副边串联谐振电路的固有谐振频率之比μ,可实现对电压增益的调节。但文中得到的恒压增益表达式较为复杂,不但与LP、LS及k有关,而且分子、分母上均含有μ2的多项式,使得补偿参数计算十分复杂、设计方法不够简单明了。文献[20]基于等效变比可调的变压器T网络模型,提出了可实现任意恒压输出的S/SP补偿的实现方法,参数设计简单直观。然而,基于特定的变压器分析模型使得该分析方法局限性较大,无法拓展至其他补偿网络。而且,现有文献中也缺乏对可调输出S/SP补偿网络的最优增益点的研究。
为解决上述问题,本文对S/SP补偿的输出恒压增益特性、输入阻抗特性进行了重构分析,给出了实现增益可调的补偿参数通用推导过程。使得系统的输出增益完全摆脱非接触变压器物理参数的影响,实现基于同一非接触变压器的不同输出恒压值的灵活调节,且设计过程简单、直观。进一步地,考虑线圈内阻对系统效率特性进行了深入分析,推导了可实现效率最大化的最佳增益取值。最后搭建了实验样机,验证了理论分析的正确性。
2 实现增益可调的通用推导方法
基于特定变压器等效模型的分析方法局限性较大,难以扩展至其他补偿网络。本节将基于IPT领域应用最为广泛的变压器互感模型,从解析表达式出发,以S/SP补偿网络为例给出实现与负载无关输出增益值任意可调的补偿参数通用推导方法。


图1 全桥S/SP谐振变换器Fig.1 S/SP compensated resonant converter
2.1 输出电压增益
基波下,图1(b)所示的原、副边网络的基尔霍夫电压方程分别为:
(1)
而输出电压可表示为:
(2)
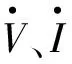
(3)
(4)
结合式(1)~式(4),可将S/SP补偿网络的交流电压增益Gv化简为:
(5)
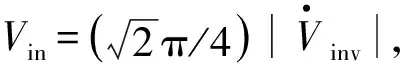
(6)
从式(5)、式(6)可知,若满足:
ZPZS+ω2M2=0
(7)
则电压增益与ZE无关,也就与等效负载RE无关。定义满足式(7)的角频率为输出电压与负载无关的系统恒压工作点,记为ωi。显然恒压点ωi处的直流电压增益GV-DC可表示为:
(8)
若希望恒压点处的增益值灵活可调,可设其大小为:
(9)
式中,r可为任意的正实数;系数8/π2为S/SP补偿IPT变换器的直流电压增益与交流电压增益之比,故予以保留。那么通过调节r的取值,即可任意调节恒压点处的增益值。将式(9)代入式(8),经化简可得到原边补偿电容:
(10)
当ωi(LP-M/r) ≫RP时,上式可简化为:
(11)
(12)
至此,通过数学推导实现了S/SP拓扑的恒压增益与负载、变压器参数均无关、可任意调节的特性,式(11)、式(12)则简单明了地给出为获得指定恒压增益(GV-DC=Vo/Vin=8r/π2)的补偿参数设计办法。
2.2 输入阻抗
图1(b)所示的S/SP补偿电路的输入阻抗Zin为:
Zin=ZP+ZR
(13)
其中,ZR为副边对原边的反映阻抗,公式为:
(14)
为分析方便,在以下推导中忽略线圈内阻RP、RS。用式(11)、式(12)代入式(13)并经分母有理化后,可得到恒压点ωi处的输入阻抗为:
(15)
当式(15)中虚部为零时,S/SP补偿网络的输入阻抗为纯阻性。根据式(15)可将其虚部为零的条件化简为:
(16)
可见副边的并联补偿电容CSP可用于调节输入阻抗。当满足式(16)时,S/SP补偿网络的输入阻抗为:
(17)
综上,为实现理想的恒压增益并保证单位功率因数,可由式(11)、式(12)以及式(16)来设计S/SP系统的补偿电容参数。
2.1~2.2节给出了实现IPT系统恒压增益任意可调的补偿参数推导过程,也可拓展至其他补偿网络,甚至是可变恒流增益特性的推导。
2.3 直观电路解释
借鉴文献[20]提出的变压器T网络模型,如图2(a)所示,其中,将模型内理想变压器的变比视作变量r可任意取值。为保持端口特性不变,此时非接触变压器的等效漏感L′L1、L′L2和等效激磁电感L′M应满足:
(18)
即可直观解释S/SP网络输出恒压增益可调且输入呈纯阻性的原因:CP、CSS分别与L′L1、L′L2谐振使得电压增益与负载无关,且大小为r任意可调、不受变压器物理参数的制约;r2L′M与CSP谐振使得输入阻抗呈纯阻性。
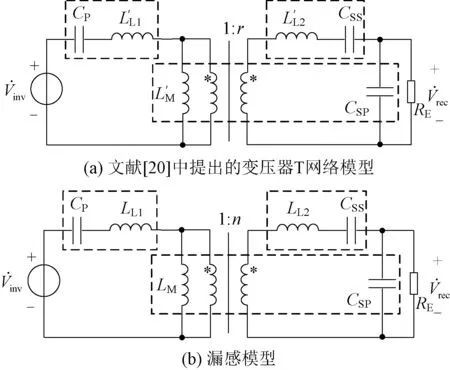
图2 变压器T模型S/SP补偿网络Fig.2 S/SP compensation circuit based on transformer T model
但采用变压器T模型进行推导的局限在于,该分析方法仅适用于S/S、S/SP或PS/S补偿增益可调的补偿参数推导,而无法直观得到其余补偿网络在增益与负载、变压器参数均无关情况下对应的补偿参数。而本文提供的通用推导办法,对于任意补偿网络均适用。
另外,当理想的恒压增益为8n/π2,由式(9)可知r=n,则式(11)、式(12)、式(16)变为:
(19)
此时变压器T网络模型中的理想变压器变比r=n,转变为常规的漏感模型,如图2(b)所示,其中,LL1、LL2为原、副边漏感,LM为原边激磁电感,且满足:LM=M/n,LL1=LP-LM,LL2=LS-n2LM。可见,文献[15]中所提出的传统的S/SP补偿方法,如图2(b),仅是本文中的S/SP拓扑的新型补偿参数设计方法的当r=n所对应的一个特例。
2.4 仿真结果

根据表1和图3中的参数,可得到当r=0.5、1、2时,S/SP补偿网络的交流电压增益|Gv|和输入阻抗角θin随系统工作频率fs变化的曲线如图4所示。
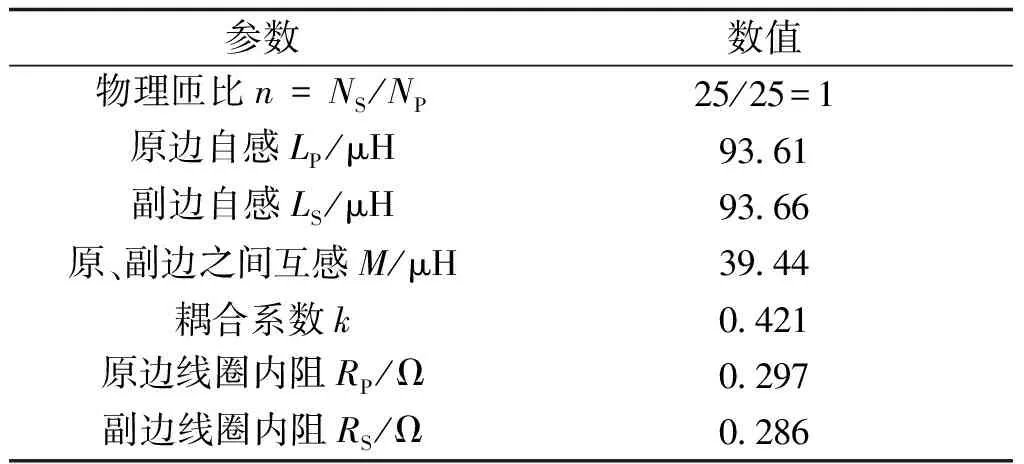
表1 非接触变压器参数Tab.1 Parameters of loosely coupled transformer

图3 补偿电容容值C随r变化的曲线Fig.3 C versus r

图4 不同r下的|Gv|、θin随fs变化的曲线Fig.4 |Gv|、θin versus fs under different designs of r
从图4(a)、图4(b)可以看出,在谐振频率100 kHz处,S/SP拓扑的输出电压与负载RL无关、输入阻抗角为零,且基于同一非接触变压器、通过调节补偿参数的大小,实现了对于输出恒压增益的调节。然而,如图4(c)所示,当r= 2时,对应着三组不同负载的增益曲线之间没有了交点,系统在r= 2时失去了输出电压与负载无关的恒压特性。这是因为当r值较大时,由式(10)可知,线圈内阻RP、RS的影响将不可忽略,将式(10)取实部简化为式(11)后带来较大的误差造成了恒压条件的丢失。而由图4(a)、图4(b)、图4(c)可看出,输入阻抗角在ωi点始终为零,证明线圈内阻对输入阻抗分析的影响不大。
3 系统效率优化
传输效率的优化是IPT系统中十分关注的问题。对于一组固定的IPT变换器参数,如何设计输出增益值使得系统效率最大化是本节关注的重点。
3.1 理论分析
图1(b)所示的S/SP补偿网络的效率η可表示为原边效率ηP与副边效率ηS的乘积:
(20)
式中,R(Z)为对应阻抗Z的实部。
将式(11)、式(12)和式(16)的补偿电容取值代入式(20),可将完全补偿点ωi处的系统效率化简为:
(21)
其中
(22)
(23)
令η对r的偏导数为零,即∂η(ωi)/∂r= 0,可求得对于一组固定的IPT系统参数,相应的最佳增益ropt为:
(24)
而最大传输效率ηmax为:
(25)
从式(24)和式(25)看出,最佳增益ropt、最大效率ηmax均随着负载电阻RE的变大而增大。
在原、副边线圈尺寸接近时,可近似认为线圈内阻之比等于线圈匝数NP、NS之比,即RS/RP≈NS/NP=n,则式(24)又可进一步表示为:
(26)
基于式(26)不难发现,对应着ηmax的最优增益ropt并不恒等于物理匝比n,因此增益可调的S/SP补偿方法,相比于传统S/SP补偿方法,有助于进一步提高系统效率。
3.2 仿真结果
下面结合表1和图3中的参数对系统效率η分析进行验证。得到完全补偿情况下的系统效率曲线如图5所示。从图5中可以看出,随着r值的变化,系统效率存在最大值,且最大值点与传统的S/SP补偿点(r=n,本示例中n为1)不一致,证明采用本文提出的S/SP新型补偿方法可提高系统传输效率;且负载电阻越大,最优增益点ropt越大、最大效率ηmax越高,与理论分析结果一致。
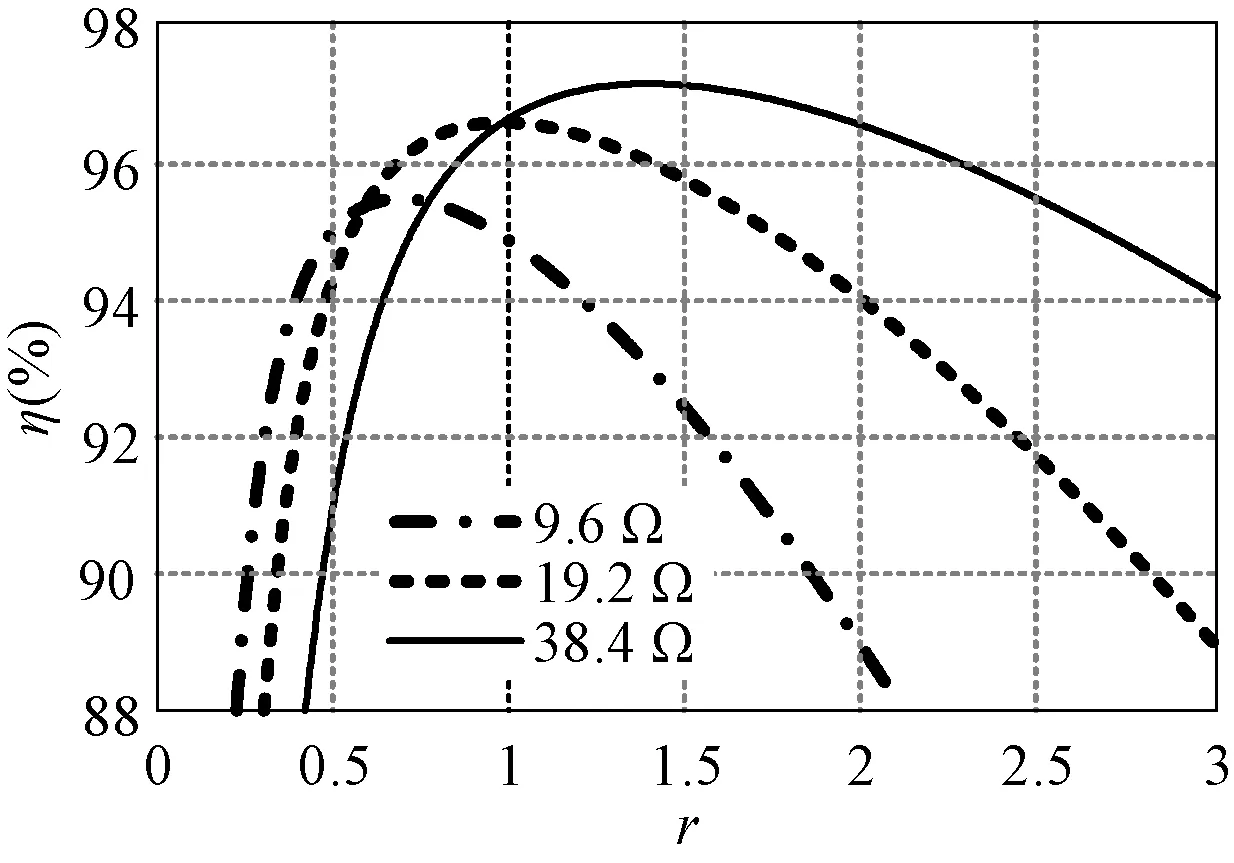
图5 不同负载下η随可调增益r变化的曲线Fig.5 η versus r under different load resistances
4 实验验证
4.1 样机参数
为验证理论分析的正确性,本文采用图1(a)所示的S/SP谐振变换器和一个现有的非接触变压器,通过改变补偿参数的大小,实现不同的输出恒压值。输入电压固定为Vin=24 V,MOS管Q1~Q4选用IRFB3307PbF,整流二极管VDR1~VDR4选用SBR10U60CT。非接触变压器采用最常见的平面螺旋线圈,参数已在表1中给出。系统频率为100 kHz,根据式(11)、式(12)和式(16),可分别计算得到r分别为不同值时对应的补偿电容计算值,见表2。实验时补偿电容的实际取值也已在表2中给出。注意到当r≤0.358或r≥2.5时,部分补偿元件呈感性,但由图4可知,此时的系统传输效率低下,实际工作中一般不会工作在此区间内。

表2 补偿电容容值Tab.2 Compensation capacitance
4.2 实测输出电压
在相同的输入电压Vin下,分别采用表2中给出的补偿电容容值,得到不同r值下对应的输出电压Vo的实测值如图6所示。需要强调,当r≥2时,由于整流二极管的电压应力限制,输入电压Vin减半变为12 V,图6中的结果为2倍的实测输出电压值。
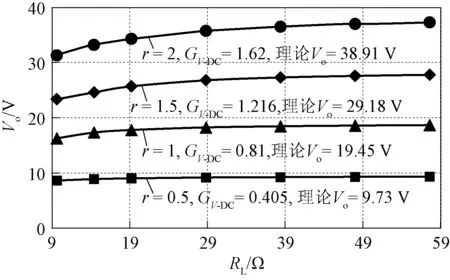
图6 不同r值下的实测输出电压典型曲线Fig.6 Measured output voltage under different designs of r
从图6可看出,系统的输出电压几乎保持恒定,小范围的输出电压波动是由于线圈内阻的影响。由于线圈内阻的存在,电压增益并不完全与负载无关,且r的取值越大输出电压随负载变化波动会越大,这是由于当r值较大时,推导式(11)、式(12)的近似条件将不再成立。以上实验结果证明了S/SP网络可调增益补偿参数设计方法的有效性。
以r=0.5为例,图7给出了不同负载下的逆变桥桥臂中点电压vinv、电流iinv和整流桥桥臂中点电压vrec、电流irec的实验波形。从图7中可以看出,vinv和iinv基本同相,证明了新型补偿方法实现了单位功率因数,且输出电压几乎保持恒定。同样,其他增益值下也具有相同的单位功率因数和输出恒压特性,这里不再重复给出。

图7 r=0.5时变负载下的实验波形Fig.7 Experimental waveforms at r=0.5
4.3 实测效率
不同的负载电阻下实测的系统效率随r变化的曲线如图8所示。实测效率曲线的形状与仿真结果基本一致,证明了效率分析的正确性。图8中标出了采用可调增益的补偿方法所能达到的效率最大值与传统S/SP补偿方法对应的效率值(对应r=1)之间的对比。显然,采用本文提出的新型补偿参数设计方法,可提高系统效率,如图8中对应负载电阻大小RL=38.4 Ω的实测结果所示,本文所提出的S/SP新型补偿方法相比传统的S/SP补偿方法效率可提升3.5%。

图8 实测系统效率Fig.8 Measured system efficiency
表3分别给出了不同负载阻值下的最佳增益ropt的计算、仿真以及实测值。对比可发现,计算结果与实测结果基本吻合,证明了最优增益点理论推导的正确性。在设计过程中,可通过合理设计IPT系统的增益,优化系统效率。
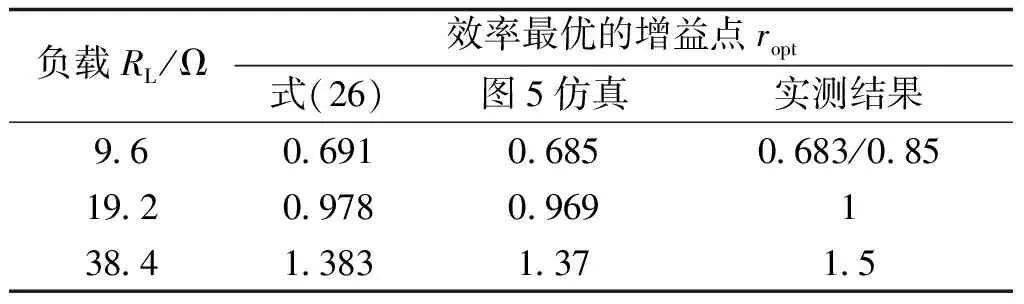
表3 最佳增益值Tab.3 Optimal voltage gain value
4.4 变耦合下的输出电压
前文所研究的均是系统在完全补偿条件下的特性,然而实际IPT系统在工作中可能会面临位置改变而造成的非接触变压器参数的变化。为探索本文提出的新型补偿方法在变参数下的特性,给出了当r=0.5、r=1和r=1.5时,系统在偏离完全补偿位置(对应k=k0=0.421)下的输出电压,如图9所示。可看出,相比传统补偿方式(r=n=1),实现输出可调后,S/SP系统依然保留了较好的变参数不敏感特性。这是由于S/SP补偿的输出电压增益(见式(9))始终与负载及变压器耦合情况无关,保证了实现增益可调下的S/SP补偿网络依然具有如文献[15,21]中一样的输出对参数变化不敏感的特性。

图9 变耦合系数k下的输出电压Fig.9 Output voltage versus coupling coefficient k
但由式(11)、式(12)及式(16)可知,由于补偿电容取值与互感M有关,在耦合发生改变后,系统中的无功能量会增大,影响系统效率。因此,本文提出的S/SP补偿方法更适用于对变参数场合下输出稳定性要求较高的场合。
5 结论
本文提出了一种可实现增益可调的新型补偿参数设计方法,使得S/SP补偿网络的电压增益与负载、非接触变压器物理参数均无关。通过调节补偿参数,即可实现对于输出电压的灵活调节,且输入端始终保持单位功率因数。此外,输出电压与变压器参数完全解耦的特性,简化了系统设计,增加了系统的设计自由度,给系统效率优化提供了空间。实验结果表明,与传统补偿方式相比,新型补偿方法对系统效率的提升高达3.5%。本文的设计思路简单明了、可移植性强,对于其他补偿拓扑如S/P、SP/S等,也可采用类似的分析方法。
