多测点无损检测法评估古建木材抗弯强度

2022-10-09王忠铖杨娜

湖南大学学报（自然科学版） 2022年1期

王忠铖，杨娜

（北京交通大学土木建筑工程学院，北京 100044）

无损检测是勘查木材内部残损状况的常用方法［1-4］.由于其对结构损伤较小，且适合现场操作，因此被越来越多地应用于木结构或木构件的损伤勘查中.古建筑木材的力学性质是评价结构健康状况的重要指标［5-6］，但可供开展破坏性力学试验的原材料十分有限，因此对于古建筑木结构的现场勘查、木材力学性质评估等工作，无损检测发挥了不可替代的作用.

抗弯强度是木材重要的力学参数，近年来，学者发现无损检测（Nondestructive test，NDT）指标与木材抗弯强度之间存在一定的相关性.朱磊等［7-8］发现落叶松旧材抗弯强度与应力波速的相关系数为0.38，低于新材的0.47；黄荣凤等［9］对针钻阻力数据进行了细分，发现阻力曲线的均值、波峰、波谷数据与局部腐朽的落叶松旧材抗弯强度的相关系数分别为0.58、0.44 和0.59；张厚江等［10］发现在95%置信度水平下，波阻模量与落叶松旧材抗弯强度的决定系数仅为0.26；李鑫［11］区分了针钻前进阻力与旋转阻力，发现由前进阻力确定的波阻模量与杉木旧材抗弯强度的决定系数为0.64，旋转阻力仅为0.34；王晓欢［12］通过频谱分析发现落叶松、软木松旧材抗弯强度与纵向动弹性模量的相关系数均大于0.81；于子绚［13］发现落叶松、云杉、软木松旧材抗弯强度与动弹性模量相关系数均大于0.76.旧材的树种、尺寸、含水率、材质状况等差异是导致无损检测指标与旧材抗弯强度相关系数离散性较大的原因之一.除此之外，现有研究大多仅测试试样单一位置的无损指标，而抗弯试样尺寸较大，试样中不同位置的木材年轮宽度、早晚材占比、纹理方向等特性并不统一，因此单一测点的无损指标往往无法反映整根试样的抗弯性质.

本文首先采用力学试验法测量了古建筑木结构旧材料的抗弯强度，然后采用“多手段、多位置”结合的方法获得了抗弯试样的无损检测指标，通过对二者进行相关性分析，讨论了测试手段、测点位置、测点数量对无损检测指标预测古建筑旧材抗弯强度的影响，以及多参数时预测模型最优自变量组合的确定方法，旨在为提高无损检测法评估古建木材抗弯强度提供参考.

1 材料与方法

1.1 试验材料

本文所使用的旧材为某藏式古建筑木结构替换下来的梁构件，构件服役期约为300 年，树种为藏青杨（Tibetan Populus cathayana），构件尺寸长约4 000 mm，宽约215 mm，高约275 mm.从梁的跨中位置和梁端位置根据《木材物理力学试材锯解及试样截取方法》（GB/T 1929—2009）和《木材抗弯强度试验方法》（GB/T 1936.1—2009）制取抗弯试样120 条，从中选取无疵试样59条.

1.2 试验方法

本文对此梁构件力学性质的关注点是其在实际环境中的抗弯强度，因此未进行含水率调整.试样制备完成后，首先进行含水率测试，测试位置见图1；随后进行基本力学性能测试，获得试样抗弯强度σb；最后，在已破坏的试样上开展应力波顺纹垂测、应力波顺纹端测、应力波横纹测试、阻力仪测试等四类无损检测，如图2（a）～（d）所示，分别获得垂测波速vsc、端测波速vsd、横纹波速vh和前进阻力Ff.

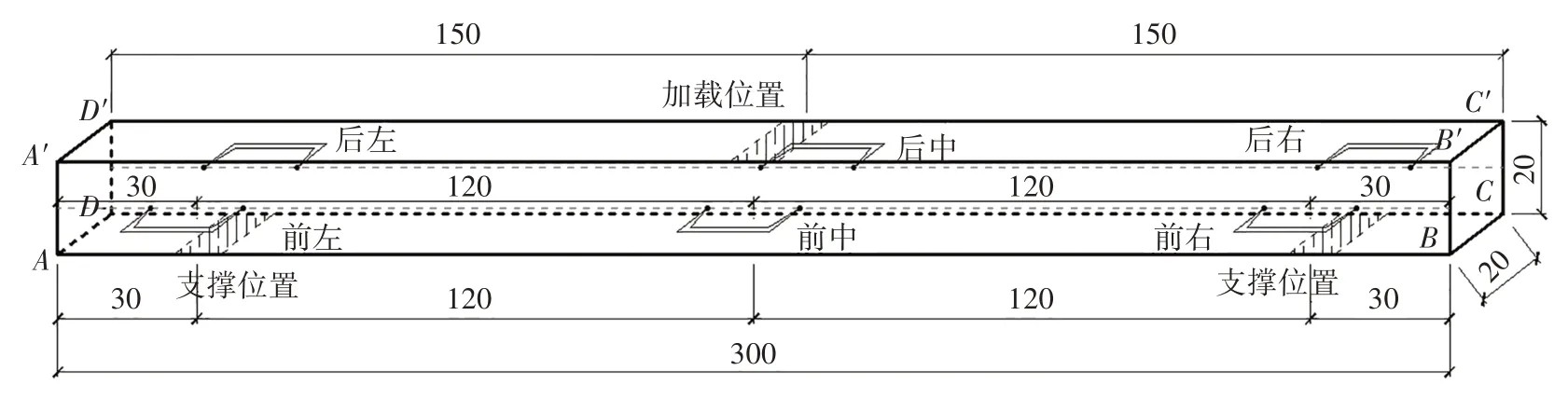
图1 含水率测试位置示意图（单位：mm）Fig.1 Schematic diagram of water content test location（unit：mm）

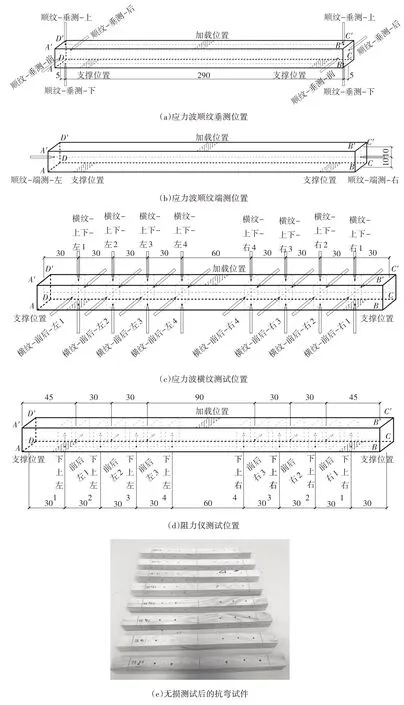
图2 抗弯试样无损检测位置示意图及测试后照片（单位：mm）Fig.2 Schematic diagram and the photo of the nondestructive test position of the bending specimen（unit：mm）

使用匈牙利FAKOPP 公司生产的Microsecond Timer 一维应力波检测仪测试应力波在试样中传播的平均速度.本文中vsc测试4 个位置，记做为vsc-i，i=1，2，3，4，分别对应上、下、前、后4 个面上顺纹垂测应力波波速；vsd测试1个位置；vh测试16个位置，记做vh-ij，i，j=1，2，3，4，其中i表示根据测试方向和位置确定的测试组，i=1，2，3，4 分别对应上下方向试样左侧组、上下方向试样右侧组、前后方向试样左侧组、前后方向试样右侧组，j表示每组中的测试位置点，其中j=1 表示支座位置测试点，j=2，3，4 依次向试样跨中递进30 mm.

使用德国Rinntech 公司生产的Resistograph 阻力仪测试钻针在前进路径上受到的阻力［11］.本文中，通过对钻入路径上所有阻力进行求和作为该测试点的阻力值Ff.对每一根抗弯试样进行14 个位置的阻力仪测试，其中由下向上钻入的测试有8 个位置，记做Ffx-ij，其中i=1，2，分别对应由下向上试样左侧组、由下向上试样右侧组，j=1，2，3，4，表示每组中测试点的位置，j=1 表示支座位置测点，j=2，3，4 依次向试样跨中递进30 mm.由前向后方向的测试有6 个位置，记做Ffq-mn，其中m=1，2，分别对应由前向后试样左侧组、由前向后试样右侧组，n=1，2，3，表示每组中测试点位置，n=1 表示由支座位置向跨中偏移15 mm位置处的测点，n=2，3依次向试样跨中递进30 mm.

除应力波速和针钻阻力外，波阻模量Fv2同样为常用的无损检测指标，本文中将波阻模量以符号M表示.

式中：Ff为针钻阻力，resi；vsd为顺纹端测波速，m/s.本文仅测试一个vsd值，因此M的个数与阻力仪测试数据的个数相同，记做Mfx-ij和Mfq-mn，下标定义同针钻阻力.

2 结果与分析

2.1 藏青杨旧材无疵试样的抗弯强度

由藏青杨旧梁制备的无疵试样的抗弯强度试验结果列于表1.作为对比，表中同时列出了《木结构设计手册》［14］中给出的甘肃青杨树种新材抗弯强度参考值.

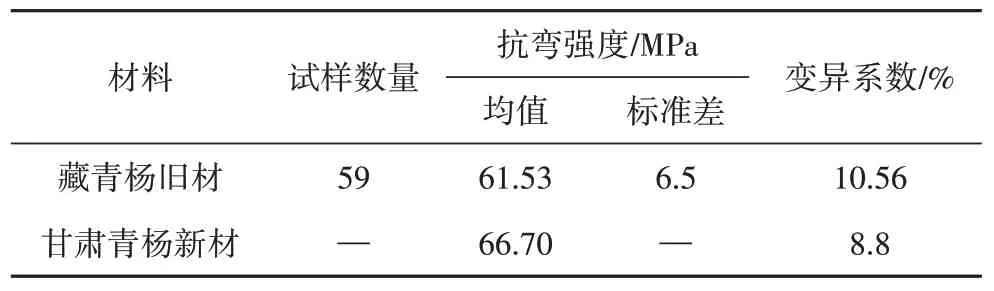
表1 旧材无疵试样抗弯强度与新材对比Tab.1 Comparison of defectless specimen between aged and new poplar

对比可见，藏青杨旧材虽然经历了300 年左右的服役期，但其无疵试样的抗弯强度仅比甘肃青杨新材低7.75%；而变异系数却比甘肃青杨新材高20.00%.由此可见，长期服役并不一定会使木材的抗弯强度显著下降，但受环境及荷载因素的影响，木材抗弯强度的离散性会明显增大［15］.

2.2 无损指标与抗弯强度的一元线性相关性分析

现有文献中关于无损检测指标与木材物理力学参数相关性的研究大多基于一元线性相关性分析，其回归模型具有简单明了、方便易用等优点.本文首先分析了无损指标均值与抗弯强度在0.05显著性水平下的一元线性相关性，结果统计于表2.

由表2 可以看出，应力波速与木材试样的抗弯强度不存在显著相关性，与现有研究结论存在一定差异，可能与抗弯试样的树种、尺寸、材质状况有关.波阻模量与抗弯强度的相关系数高于阻力值与抗弯强度的相关系数，其中前后方向波阻模量与抗弯强度的相关系数最高，为0.482，校正决定系数为0.219.此外，对于这两类无损指标，前后测试方向与抗弯强度的相关系数均高于下上测试方向，这是由于抗弯试样为弦向受弯，抗弯强度由所有年轮中早晚材特征共同决定，而钻针由前向后钻入可以反映所有年轮中早晚材的特性，因此与抗弯强度的相关性更高.

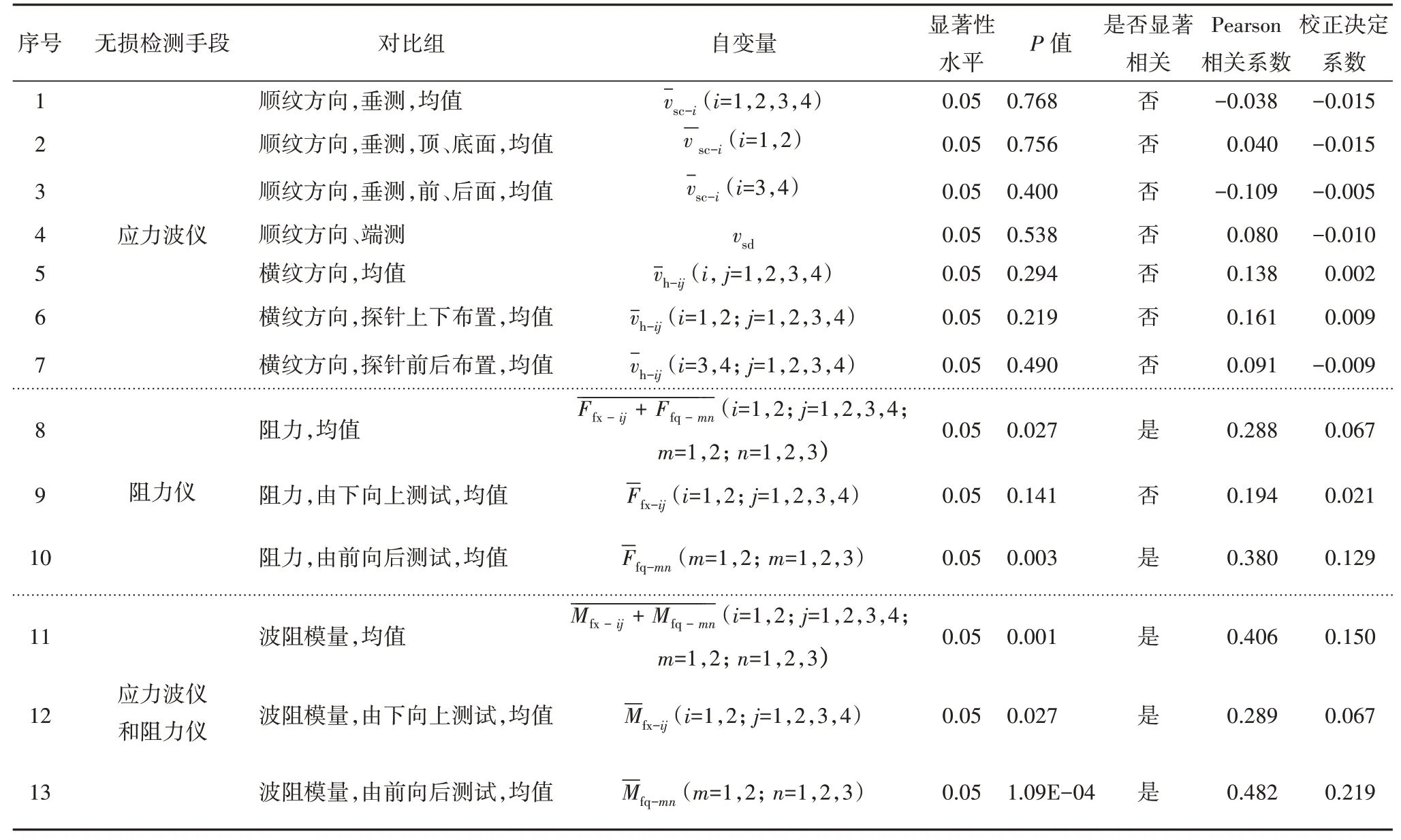
表2 抗弯强度与无损检测指标的一元线性相关性分析Tab.2 Unary linear correlation analysis of σb and NDT index

前后方向阻力均值及前后方向波阻模量均值与试样抗弯强度的关系如图3所示.

图3 前后方向阻力值均值及波阻模量均值与抗弯强度的关系Fig.3 Correlation between mean Ffq，mean Mfq and σb

2.3 无损指标与抗弯强度的多元线性相关性分析

增加模型中自变量的个数，在理论上可以提高相关系数，但自变量过多又会增加不必要的测试工作量，同时增加对木构件的损伤.因此，在更高的相关系数和更少的工作量间应尽量做到平衡.此外，由于木材纹理的差别，不同测点得到的无损指标与木材性质间可能存在差别.本节讨论了增加测点数量对模型相关系数的影响，以及在测点数量相同时，不同测点位置对模型相关系数的影响.

将应力波横纹上下、前后波速，阻力仪下上、前后方向阻力值，下上、前后方向波阻模量共计6 类无损参数进行不同测点数量、不同对称测点位置的组合，并分别与抗弯强度进行相关性分析.将得到的相关系数进行对比，结果如图4所示.

由图4（a）可见，随着测点数量的增加，模型与抗弯强度的相关系数逐渐升高；当测点数量一致时，前后方向波阻模量与抗弯强度的相关系数高于其他无损指标.由图4（b）～（d）可见，对于阻力值和波阻模量两类无损指标，前后方向测试指标与抗弯强度的相关系数普遍高于下上方向，与前文结论一致.不同测点位置同样会影响无损指标与抗弯强度的相关系数，由图4（b）可见，对于前后方向波阻模量、阻力值两类无损指标，左、右测点3 的自变量组合与抗弯强度的相关系数略低于左、右测点1 或2 的组合，这是由于测点3 靠近试样跨中的破坏位置，与试样木材原始材质状况差异最大；对于下上方向的波阻模量、阻力值两类无损参数，随着测点由试样两端向跨中过渡，相关系数逐渐降低，同样与靠近跨中处木材材质状况与原始状况差异较大有关.

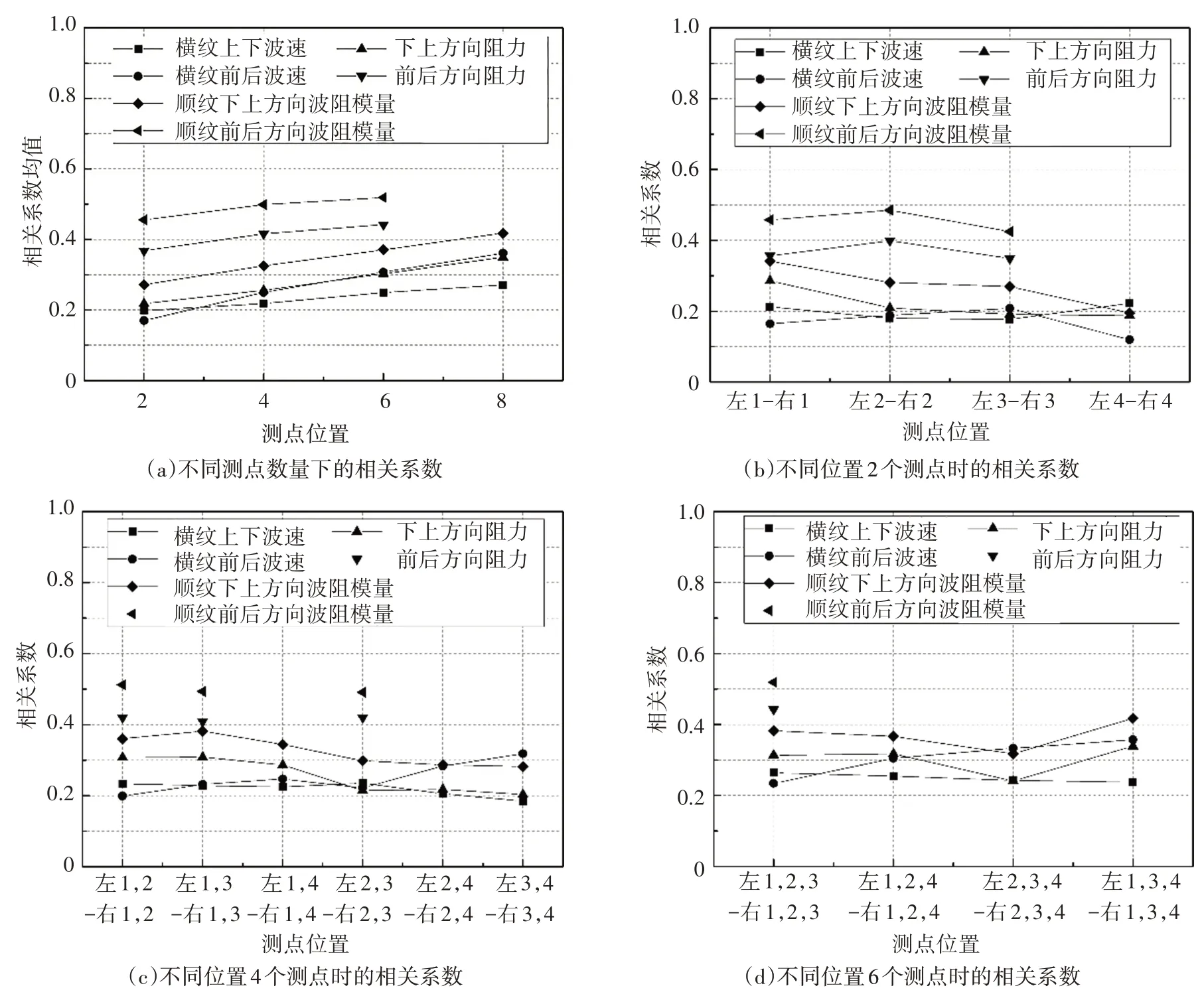
图4 不同测点数量、位置时无损检测指标与抗弯强度的相关系数Fig.4 Correlation coefficient of NDT index and σb for different number and location of measuring points

2.4 预测抗弯强度参数的最优自变量组合

逐步回归法（Stepwise regression method）［16］是回归分析中常用的寻找最优自变量组合的统计学方法.其基本思想是将自变量逐个引入模型，每引入一个自变量进行一次F 检验，并对所有已选入的自变量逐一进行t检验，当较早引入的自变量由于后面自变量的引入变得不再显著时，将其删除，从而保证每次在引入新的自变量之前回归方程中仅包含显著变量.逐步回归的过程是一个反复的过程，直到既没有显著变量选入回归方程，也没有不显著变量从方程中剔除为止，从而保证最后所得的所有自变量的集合是最优的.本文中自变量共计75 类，使用SPSS 分析软件进行多自变量下木材物理力学参数预测的逐步回归分析，表3、表4 分别为预测抗弯强度的逐步回归分析结果及模型参数，其中B为非标准化系数，VIF为方差膨胀系数.

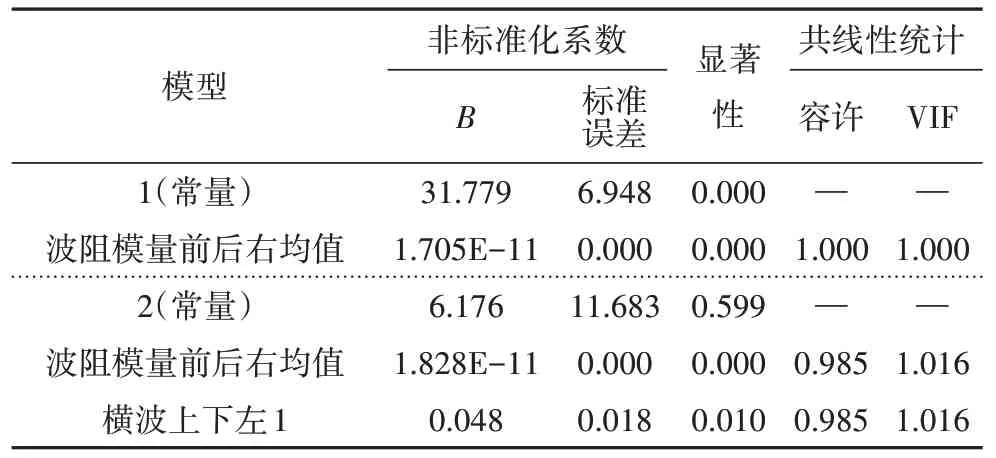
表4 无损指标与抗弯强度的逐步回归模型参数Tab.4 Stepwise regression model parameters of NDT index and σb

由表3 可见，使用前后方向试样右侧测点波阻模量均值和试样左侧测点1 上下横纹波速这两种无损指标的组合（后称强度SR模型）时，相关系数可达到最大值0.581，校正决定系数为0.313，较前后方向波阻模量均值的一元模型分别提高20.54% 和42.92%，表明多测点无损检测法可以有效提高木材抗弯强度预测的准确性.