基于应变信号时频分析与CNN 网络的车辆荷载识别方法
2022-10-09周云赵瑜郝官旺方亮
周云,赵瑜,郝官旺,方亮,4
(1.工程结构损伤诊断湖南省重点实验室(湖南大学),湖南长沙 410082;2.湖南大学土木工程学院,湖南长沙 410082;3.周绪红院士湖南大学新型结构体系研究中心,湖南长沙 410082;4.湖南农业大学水利与土木工程学院,湖南长沙 410128)
桥梁是现代交通的重要组成部分,在国民经济与民生生活中起着至关重要的作用.截至2019 年,全国公路桥梁87.83 万座,比上年增加2.68 万座,其中,特大桥梁5 716座,大桥108 344座[1].相关研究显示[2],我国2000年1月至2012年3月期间的157座失效桥梁的统计结果中,高达10.83%的桥梁失效是由车辆超载直接导致的.因此,实时监控桥面车辆重量,对于桥梁健康检测具有十分重要的意义.
2008 年,李忠献等[3]提出了一种基于BP 神经网络的桥梁移动车载的分阶段识别方法,通过分阶段识别技术,对桥梁上的车辆的位置、速度和荷载等信息进行在线、实时地识别.利用有限元模型模拟了大量训练样本,采用正则化方法修正误差性能函数,通过遗传算法对初始权值进行优化,模拟结果表明:该方法识别精度高、收敛速度快,且具有较强的抗噪性和鲁棒性,但采用该方法训练BP(Back Propagation)神经网络时需提前获得车辆的荷载时程信号.
2009年,Kim 等[4]提出了使用人工神经网络(Artificial Neural Network,ANN)作为桥梁动态称重(Bridge Weigh-in-Motion,BWIM)系统的信号分析算法,意在尝试从BWIM 系统的时域应变数据中提取有关重型车辆的信息(例如重量、速度和轴数),并通过试验方法验证了该方法的可行性,但其荷载识别误差在±20%之间.
2012年,González等[5]通过在桥梁全跨布置多个称重传感器,利用监测所得的多个结构应变响应信号对传统BWIM 系统测试方程中存在的病态项进行了消除,提高了对车辆实际轴重求解的效率,但该方法仍未摆脱传统BWIM 系统高昂的设备以及后期费用问题.
2012 年,夏樟华等[6]为了得到桥梁上移动车辆荷载,提出了一种基于应变响应与移动荷载回归方程的移动荷载识别方法.首先通过小波变换消除应变响应的噪声,其次通过响应特征估算车辆过桥的时间及速度,最后建立移动荷载与应变响应的二次回归方程.研究结果表明:该方法的误差率基本小于17%,但该荷载识别方法仍具有较大的识别误差.
2016 年,赵华等[7]比较了连续小波变换(Continuous Wavelet Transform,CWT)、离散小波变换(Discrete wavelet transform,DWT)和平稳小波变换(Stationary Wavelet Transform,SWT)对提高FAD 信号车轴信息识别的特点、优势以及使用范围,提出了利用小波变换技术提高FAD传感器对车轴信息识别精度的方法,并通过野外试验验证了该方法的可行性.但是,其仅对比了小波变换这一类时间频分析对于提高FAD传感器的车轴信息识别精度的效果.
2016年,Bao等[8]通过测量在桥梁上施加外加荷载下桥梁结构的剪应变响应信号,并利用BWIM 系统实现了对行驶车辆实际轴重的识别.
2017 年,Lydon 等[9]基于光纤传感器,研发出了一种用于识别车轴的BWIM 系统,该系统不但能获得准确应变响应信号,还能有效缓解噪声对测试信号的影响.
2020 年,邓露等[10]为准确了解桥梁动态称重(BWIM)技术在不同类型桥梁上的适用性,基于公路桥梁通用图集建立了典型截面和跨度的桥梁模型,并利用数值仿真方法研究了桥梁跨径、截面类型、车辆类型、传感器测点位置、路面平整度、测量噪声、行驶速度等重要因素对BWIM 方法识别效果的影响,进一步验证了BWIM方法的实际应用价值.
综上所述,相关学者的研究结果表明:采用神经网络对于车辆进行荷载识别能够避免传统BWIM 系统需要安装复杂且昂贵设备的问题,但采用神经网络进行荷载识别时的识别精度有待提高,且训练样本的采集工作较为困难.因此,本文提出了一种基于应变信号时频分析与CNN网络的车辆荷载识别方法对车辆总重进行识别,避免为求荷载时程而需要提前采集荷载时程信号作为训练样本的弊端,同时,采用CWT 处理应变信号以提高荷载的识别精度.本文主要做了如下研究工作:首先分别利用短时傅里叶变换(Short Time Fourier Transform,STFT)、维格纳-维利分布(Wigner Ville Distribution,WVD)以及CWT变换对桥梁跨中应变响应进行时频分析,获得时域信号难以展示的时频特征,并生成大小为64×64 数值矩阵;其次分别将上述时频分析方法生成的数值矩阵作为CNN网络的输入数据进行车辆荷载的训练识别,并选取训练识别效果最优的CWT 变换作为最终的应变信号时频处理方法,同时采用CNN 网络的回归学习功能,在训练少量CWT 变换处理的数值矩阵后,直接建立输入数据与车辆荷载的映射关系,从而具备对未知车辆荷载识别的能力;最后通过车桥耦合试验验证了该方法的可行性.
1 基于CNN网络的移动荷载识别
1.1 时频分析
为将一维应变信号转化为能够输入CNN网络的二维数值矩阵,同时突出一维应变时域信号的频域特征,提高CNN网络对于应变信号特征的提取能力,本文需要将采集的原始应变信号进行时频变换处理.常见的时频分析方法有STFT、WVD和CWT等.
1.1.1 STFT变换
Gabor 于1946 年提出了STFT 的概念[11],通过对时域信号进行加窗处理,并对窗内信号进行傅里叶变换.通过在信号时间轴上不断地移动窗函数并不断地进行傅里叶变换,便可得到任意时刻t附近的时间局域化频谱.对于离散的时域信号s[n],STFT 的数学表达式为:
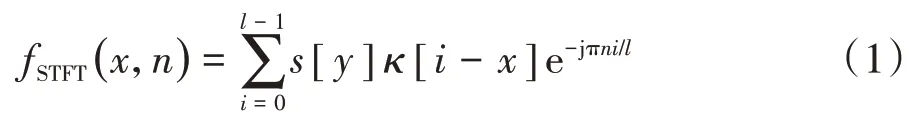
式中:κ[n]为窗函数;l为窗长;x为频率点序号;i为计数变量.
1.1.2 WVD分布
WVD 是一种行之有效的时频分析方法,被定义为信号中心协方差函数的傅里叶变换[12],具有平移不变性、边界有界性以及可叠加性等诸多优点.
该方法能在时频域内保持较高的计算分辨率,同时,能够较好地反映信号的瞬时频率信息.对于信号x(t)的处理过程的WVD数学表达式为:

式中:xa(t)为原始信号;xa*(t)为的复数共轭.
1.1.3 CWT变换
CWT 作为小波变换的一种,对输入信号的类型无特殊要求,可对应变、位移及加速度等信号进行分析变换.CWT 变换具有较强的时-频定位能力,在结构健康监测领域内获得到了极大的关注.CWT 变化中最重要的步骤是选择小波基函数(Wavelet basis function),它直接影响后续小波分析的准确性和信号特征提取的有效性,其中常用的小波基函数主要有Morlet、Haar 及其Meyer 等.根据相关研究表明[13],采用Morlet基函数的CWT分析方法在提取结构动态响应信号特征时具备更加理想的效果.Morlet小波基函数是具有呈平方指数衰减趋势的余弦函数,采用Morlet基函数的CWT变换可表示为:

式中:ψ*(t)表示ψ(t)的复共轭.而Morlet小波基函数为一余弦函数,其在时频域的函数表达分别为:
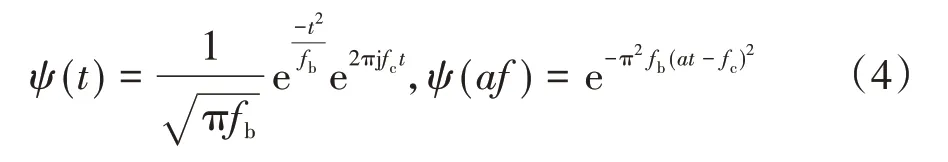
式中:fb为频率带宽参数;fc为小波中心频率.
CWT 变换能够较好地从时间、频率及幅值等方面对非平稳信号的时频局部特征进行描述,还可以通过平移/伸缩窗函数的方式对信号细节特征进行提取,是一种较为理想的时频分析工具.
1.2 CNN网络搭建
为了建立应变信号时频特征与车辆荷载的映射关系,本文提出了基于应变信号时频分析与CNN 网络的车辆荷载识别方法.经过反复网络调节,在获得最佳训练识别效果后,本文选择了一个拥有4 个卷积层、4 个池化层、1 个全连接层的CNN 网络作为车辆荷载识别网络,网络中各部分作用[13]如下:
1)输入层(Input layers).本文中的CNN 网络输入数据是利用双线性插值算法调整应变时频信号大小后生成的二维数值矩阵,大小为64×64.
2)卷积层(Convolutional layers).卷积神经网络中的每一层卷积层都有若干个卷积核,每一个卷积核中的参数都是通过反向传播算法最优化得到,且每个卷积核都承担着不同特征的识别任务,为获得最佳识别效果,经过反复网络调试,决定分别在第1层卷积层设置8 个3×3 卷积核,在第2 层卷积层设置16 个3×3 卷积核,在第3 层卷积层设置32 个3×3 卷积核,在第4层卷积层设置64个3×3卷积核.

式中:k代表卷积核;Mj代表第j个特征图;b代表偏置;l代表第l层.
3)池化层(Pooling layers).池化也称下采样,存在于卷积层后面,其功能主要在于降低网络参数量.通过池化作用选择池化区域中感兴趣的值而舍弃其它值,即降采样,参与计算的数据量也会因此下降,在一定程度上达到了防止过拟合的目的.例如,“最大池化处理”作用是选择池化区域中的最大值作为输出值;“平均池化”作用是选择池化区域中的平均值作为输出值.本网络中采用的是“最大池化(max pooling)”.
4)激活函数(Activation functions).卷积、池化等都是对数据的线性处理,为了使用CNN 网络模型学习和理解复杂和非线性问题,需要在网络中引入非线性特征——激活函数.常见的激活函数有Sigmoid、Tanh、Relu 等,相比于Sigmoid 和Tanh 函数,Relu 函数更加利于网络进行反向传播和参数更新,并且其还具有防止梯度消失的功能,因此本文中的激活函数将采用Relu函数.
5)全连接层(Fully connected layer).在CNN 结构中,卷积层和池化层模仿着人类眼睛对目标局部特征搜索的效果,而全连接层会连接其前一层的所有神经元,目的是让全连接层可以整合卷积层或者池化层中提取的局部特征信息,提升CNN网络的识别性能.
6)输出层(Output layers).常见的CNN 网络主要有两大功能,即分类功能和回归功能.相比于分类CNN 网络只能输出有限的几类结果,回归CNN 网络则具备输出连续任意数值的能力.回归CNN 网络将最后一层卷积层的卷积结果全连接到一个神经元上作为回归识别结果,如图1所示.

图1 回归预测CNN网络模型Fig.1 CNN model of regression prediction
在回归分析中误差以及损失函数的计算式为式(6).

式中:yi为训练数据中第i个数据的真实值;y′i为训练数据中第i个数据的预测值.
综上,本文将采用CNN网络回归学习方法,在训练少量车辆荷载值对应的应变信号时频数据后,直接建立车辆荷载与应变信号的映射关系,从而具备识别输出连续未知荷载的能力.采用的CNN 网络结构及其网络参数设置如图2所示.
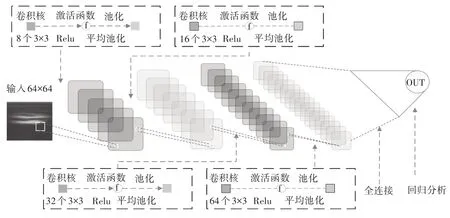
图2 CNN网络模型Fig.2 CNN network model
1.3 车桥耦合数值模型
为建立CNN 网络训练数据库,本文将建立如图3所示的车桥耦合模型,并通过数值模拟车辆以不同速度、不同荷载过桥时的桥梁应变响应.

图3 车桥耦合模型Fig.3 Vehicle bridge coupling model
在车辆建模中,充分考虑车身、悬架、轮胎等各部分的特性及其运动方式,并以弹簧阻尼系统为原型,将车辆各部分简化为由一系列质量、阻尼、弹簧组合而成的多自由度空间体系.以四自由度平面双轴车为例,建立车桥动力方程如下.
车辆子系统的振动方程可以表示为:
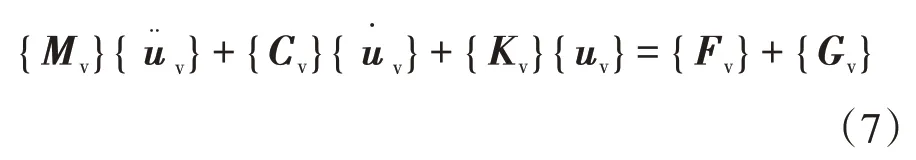
式中:Mv、Cv、Kv均为常系数矩阵;Fv+Gv为车桥接触点力对应的等效单元节点力,其取决于接触点的桥梁振动速度、振动位移以及车轮速度、位移等.
桥梁子系统的振动方程为:
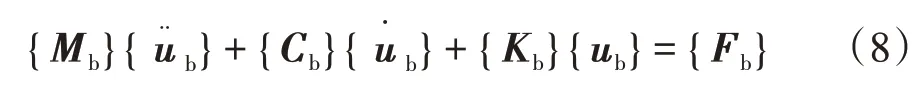
式中:Mb、Cb、Kb均为常系数矩阵;Fb为车桥接触点对应的等效桥梁单元节点力,其取决于接触点的桥梁振动速度、振动位移以及车轮速度、位移等.
其中质量矩阵为:
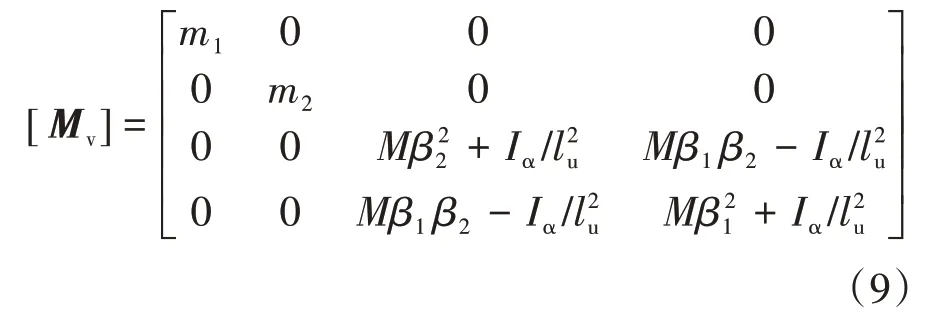
阻尼矩阵为:
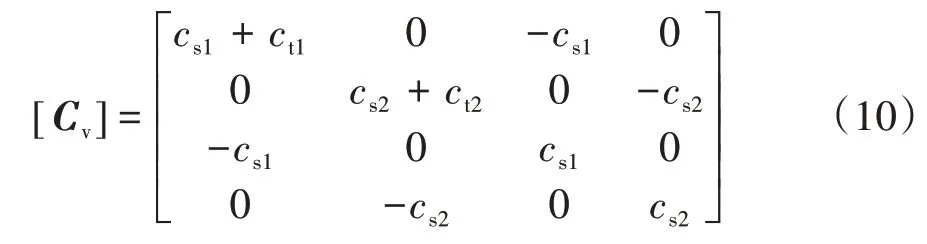
刚度矩阵为:
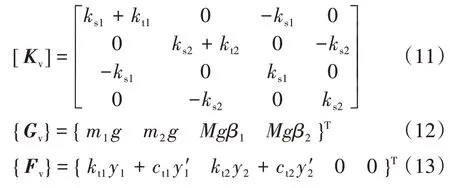
式(9)~式(13)中参数的意义见表1.
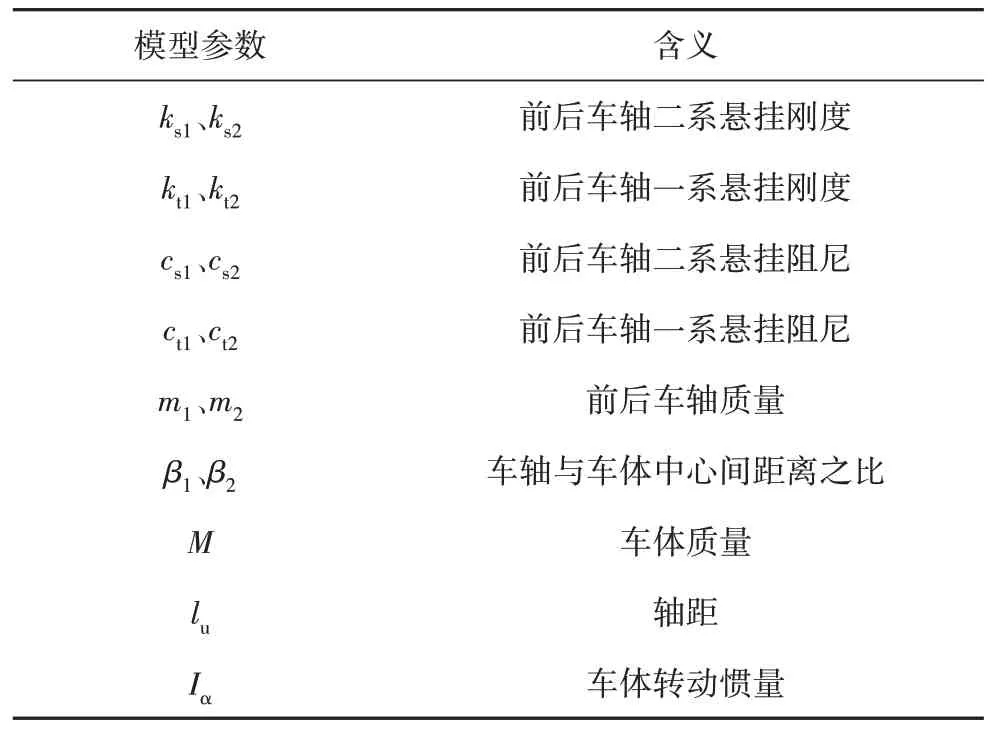
表1 车桥耦合参数表Tab.1 Vehicle axle coupling parameters
本文将在Matlab 平台中建立车辆子系统,并将车辆振动方程的右边项{Fv}+{Gv}施加于车辆子系统中各个自由度的节点上,并调用ANSYS12.0 的时程分析模块计算各子步时程.
第1 步:预设桥梁子系统的位移、速度均为零,并以路面粗糙度作为激励,求解车辆子系统的解,即所有车轮与桥梁的接触力时程Fv(t).
第2 部:将第1 步的迭代结果——接触力时程Fv(t)对应的等效节点力序列施加于桥梁上,并求解桥梁子系统,得到桥面的运动状态.
第3 步:在第2 步获得的桥面运动状态基础上,叠加路面粗糙度作为系统新的激励,并再次求解车辆子系统,得到车轮与桥面新的接触力时程.
第4 步:计算第3 步接触力时程与第1 步(或前一次迭代)计算的接触力时程的误差,并判断是否满足迭代收敛条件.若满足,则代表完成了所有迭代计算,否则进入新一轮迭代过程,并重新计算第2 至第4步.
第5 步:迭代计算至达到收敛条件,将求解得到的迭代计算结果传递给ANSYS 有限元模型进行求解,进而获得桥梁动应变响应时程.
1.4 面粗糙度模拟
在车桥耦合系统中,车辆内部振动激励源不仅来自桥梁挠曲变形,还来自随位置变换引起的不同路面粗糙度.而该粗糙度可以看做是一种平稳、各态零均值的随机高斯函数.一般情况下采用确定性函数模拟路面粗糙度分布,例如,功率密度函数(Power spectral density,PSD),通过采集实际路面粗糙度数据后,通过拟合便能得到关于路面粗糙度的PSD 函数曲线[14].
本文主要依据ISO—1972 规范建议标准,对路面粗糙度进行模拟,其表达式为[15]:

式中:Ω0为标准空间采样率;Ω为空间采样率,表示采样空间内,高频采样与低频采样的采样率分界线,通常取值大小为(π/2)cycle/m.
在实际模拟路面粗糙度时,通常采用相关级数理论,利用计算好的功率密度函数(PSD)进行模拟,其表达式如下:
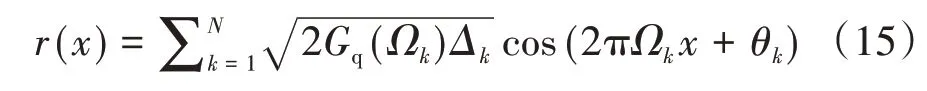
2 数值模拟验证
2.1 车桥耦合模型建立
为了验证所提车辆荷载识别方法的可行性,本文建立了车-桥耦合计算模型进行模拟.通过Matlab R2019b 和ANSYS 12.0 分别建立了两轴车辆模型和桥梁模型,由Matlab 主程序控制桥梁与车辆的子系统在每一个时刻进行耦合迭代至收敛,同时考虑路面粗糙度的影响,采用国家标准《机械振动道路路面谱测量数据报告》(GB 7031—2005)C 级路面[16],最终输出行车道跨中节点的动应变时程响应.
本文根据研究的需要,采用两轴车的半车模型,如图3 所示,考虑了车体浮沉、俯仰、两车轮竖向位移4 个自由度,该模型基本能反映车辆各部分结构特性参数,符合本文研究中车-桥耦合模拟计算的精度,其车辆参数取值见表2.
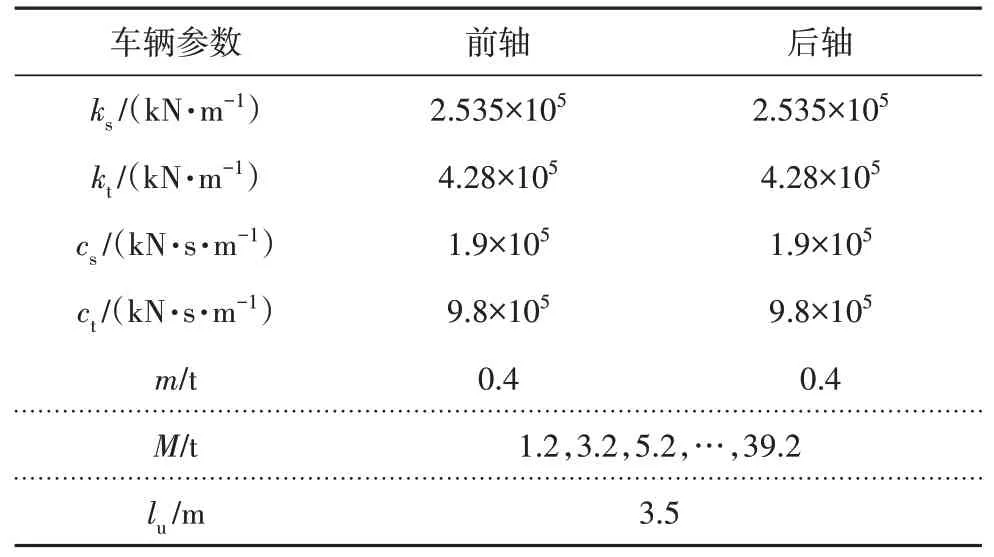
表2 车辆参数表Tab.2 Vehicle parameter table
对于桥梁模型建模方面,采用钢筋混凝土梁板式桥梁结构,为了提高计算效率,在ANSYS 12.0 中采用梁格法利用纵横向梁单元建立整座桥梁结构体系,如图4 所示.桥梁总长约30 m,宽度约12 m,由5根纵向T型梁组成,每根T梁的抗弯刚度为EI=1.08×109N·m2,质量阻尼系数α=1.76,刚度阻尼系数β=1.120×10-3.每隔6 m 设置横向隔板连接各纵梁,并且在该桥上对称设置两条车道,并将第一条车道作为模拟跑车车道.

图4 桥梁ANSYS模型(单位:cm)Fig.4 ANSYS model of bridge(unit:cm)
为验证所提出的CNN网络对移动车辆荷载的识别效果,本文通过车-桥耦合模拟试验建立了CNN网络的训练数据集,模拟工况如下:首先,将车辆荷载分为2、4、6、…、38、40 t,共计20 个荷载工况分组;其次,将每个荷载工况分组按照车辆速度分为5、5.25、5.50、5.75、…、14.50、14.75 m/s 等40 个速度工况,总计20×40=800 组工况;最后,进行模拟跑车试验,并选取具有代表性的跨中应变响应作为目标信号,部分跨中应变信号如图5 所示,其中,原信号采样频率为100 Hz,图5为取原信号中1/10数据作图.
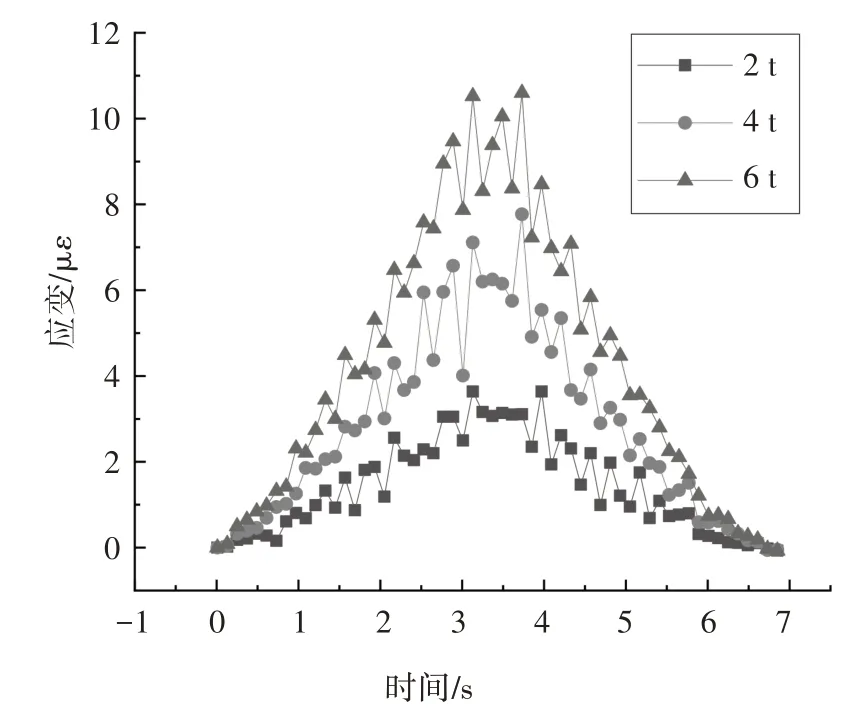
图5 桥梁跨中应变(v=5 m/s)Fig.5 Strain signal of the bridge midspan(v=5 m/s)
2.2 应变信号时频分析
时频分析的基本思想是:设计时间和频率的联合函数,并且用该函数同时描述信号在不同时间和频率上的能量密度或强度关系.时间和频率的这种联合函数简称为时频分布.利用时频分布来分析信号,能给出各个时刻的瞬时频率及其幅值,而幅值与信号能量有关,信号能量与输入激励有关,因此,合理地分析并表达出应变信号的时频分布关系,对于基于应变信号时频分析与CNN网络的车辆荷载识别至关重要.本文主要研究对比了STFT 变换、WVD 分布、CWT变换的应变信号分析效果.图6为4 t重小车分别以5.0 m/s、6.0 m/s的速度通过简支桥梁时,桥梁跨中产生的应变响应.

图6 桥梁跨中应变(车重4 t)Fig.6 Strain of bridge midspan(vehicle weight 4 t)
STFT 变换:STFT 通过对时域信号进行加窗处理,并分别对窗内信号进行傅里叶变换,获得特定时刻附近的时频图.而窗函数的应用能够有效地避免信号片段截取时的频率泄露问题,常见的窗函数有费杰窗、汉宁窗、海明窗等,本文采用常见的海明窗进行加窗操作,其中信号长度分别为692 和581,窗长为128,重叠点数为127,采样频率为100 Hz,傅里叶点数为128,时频分析结果如图7 所示.可以看出车辆经过桥梁时,对于应变信号低频部分的幅值有较大的影响,且随着车辆离跨中越近,应变幅值越大.从力学角度分析得知该幅值大小受车辆荷载大小影响,且由图7(a)和图7(b)可以看出,应变幅值对车速等因素并不敏感.
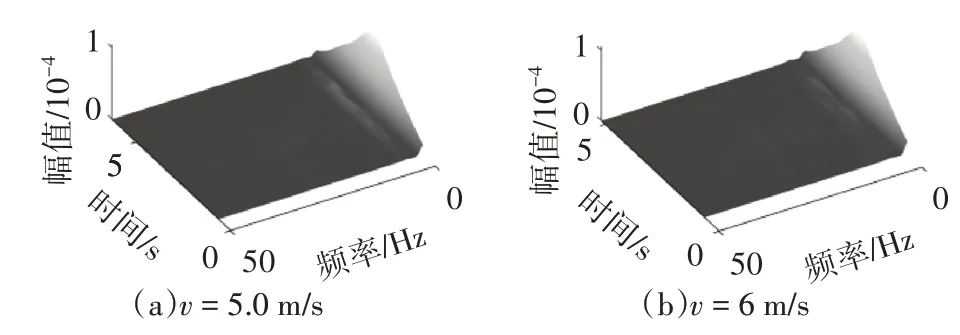
图7 应变信号的STFT三维图(车重4 t)Fig.7 STFT 3D diagram of strain signal(vehicle weight 4 t)
WVD 分布:WVD 分布具有平移不变性、边界有界性以及可叠加性等诸多优点.WVD 分析可以看作是信号自相关函数的傅里叶变换,它是信号的二次时频分析结果,因此,利用WVD 处理应变信号,实际上反映了应变信号自相关函数的频域随时域的变化过程.本小节中,其对应变信号的时频分析结果如图8 所示,其中,采样频率为100 Hz,信号长度分别为692 和581.由图7 和图8 的分析结果可以看出WVD分析结果的数量级与STFT 分析结果的数量级约成平方关系.
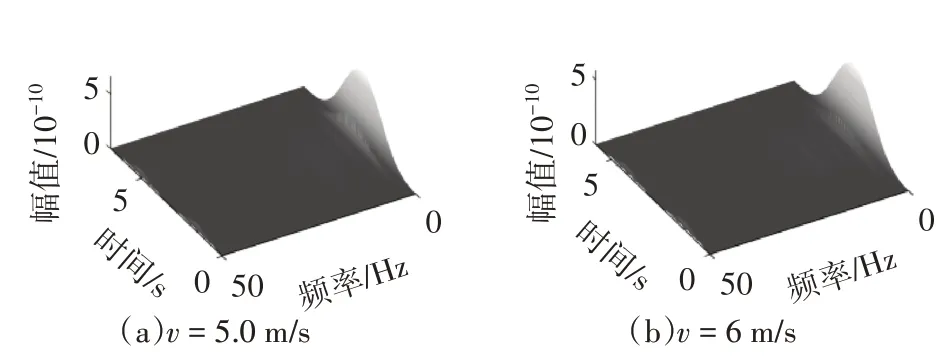
图8 应变信号的WVD三维图(车重4 t)Fig.8 WVD 3D diagram of strain signal(vehicle weight 4 t)
CWT 变换:CWT 变化中最重要的步骤是选择小波基函数,它直接影响后续小波分析的准确性和信号特征提取的有效性.CWT变换能够较好地从时间、频率及幅值等方面对非平稳信号的时频局部特征进行描述,相比于STFT 变换,CWT 变换可以通过平移/伸缩窗函数的方式对信号细节特征进行提取.本文选择Morlet 小波对应变信号进行时频分析,其中,信号长度分别为692 和581,采样频率100 Hz,最大尺度1 000,时频分析结果如图9 所示.从图7 和图9 可以看出,相比于STFT 变换,由于CWT 变换能自动调整窗函数以适应信号的变化,因此CWT 的分析结果在低频时具有较高的分辨率,而且应变信号主要由低频信号组成,因此在处理应变信号时CWT 变换是一种比STFT变换更理想的时频分析工具.
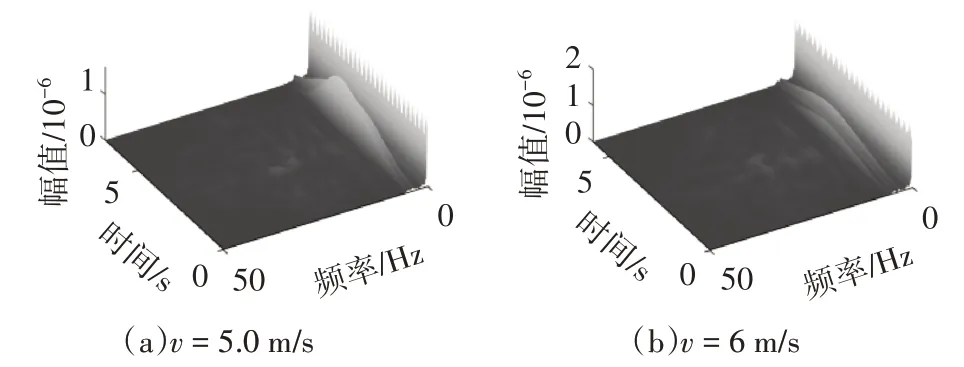
图9 应变信号的CWT三维图(车重4 t)Fig.9 CWT 3D diagram of strain signal(vehicle weight 4 t)
由以上时频分析结果可以看出,应变信号幅值主要由低频分量贡献,随着频率越高其对应变的贡献就越小.比较STFT变换、WVD 分布以及CWT变换对桥梁跨中应变信号的处理效果,可以发现STFT 变换和WVD 分布对该信号的处理效果较为一般,而采用Morlet小波的CWT变换在低频部分处具有较高的分辨率,能清晰显示信号间因为车速等因素不同而产生的微弱差别,更有利于CNN 网络对于应变信号的特征提取.
2.3 数值矩阵
从力学角度来分析,车辆荷载作用于桥梁桥体使得桥梁产生弯曲变形,桥梁跨中底部应变信号的信号幅值大小则间接反映了车辆荷载的大小,将一维的原始应变信号在频域中展开,能够在不同频率上更多地展示出应变信号与车辆荷载的间接关系,更加有利于CNN 网络提取信号的相关特征,便于建立应变信号与车辆荷载的映射关系.为了更好地将上述特性用于CNN 网络的训练中,本文采用时频数值矩阵而非时频图的RGB 图像作为CNN 网络的输入数据.
以CWT 方法为例.图10(a)为时频分析所得数值矩阵的三维图,其中的元素值反映了真实的时频分析结果,且能反映两图间数值的绝对大小.例如,因为荷载大小的差异,图10(a)和图11(a)中的数值相差一个数量级,而图10(b)和图11(b)为时频分析数值矩阵转化为RGB 图像后的像素值所作三维图,其中像素值范围在0~255 之间,因此不能反映出原数值矩阵间元素的绝对大小.

图10 应变信号的CWT分析图(车重2 t,v=5 m/s)Fig.10 CWT diagram of strain signal(vehicle weight 2 t,v=5 m/s)

图11 应变信号的CWT分析图(车重40 t,v=6 m/s)Fig.11 CWT diagram of strain signal(vehicle weight 40 t,v=6 m/s)
综上所述,由于时频分析求得的数值矩阵元素大小与车辆荷载的大小相关,本文将采用双线性插值算法,将时频分析结果转化为64×64 的数值矩阵作为CNN 网络的输入数据,而非传统地将时频分析生成的RGB图片作为CNN网络的输入数据.
2.4 神经网络训练测试
基于2.1节提出的车桥耦合模拟试验,在建立训练数据集后,利用CNN 网络模型进行车辆荷载的训练识别验证.对于CNN 网络模型,其输入数据为2.3节所示64×64 的数值矩阵,且计算数值矩阵所涉及的时频分析方法参数取值与2.2 节对应的时频分析方法参数取值一样.同时,CNN 网络的输出值为车辆总重值,即CNN 网络输入数据为一个64×64 的数值矩阵,输出数据为一个车重数值.
首先,随机选取每个荷载工况分组里的32 组应变信号作为CNN 网络的训练数据,选取剩余8 组应变信号作为CNN网络的识别数据;其次,分别对上述数据进行STFT 变换、CWT 变换和WVD 分布生成大小为64×64 的数值矩阵作为CNN 网络的输入数据;最后,对比分析基于上述输入数据的CNN 网络的训练识别结果,最终选出最有利于CNN 网络训练识别的时频分析方法.
2.4.1 CNN网络训练结果
由图12 可以看出,基于CWT 变换和STFT 变换生成的时频数值矩阵作为训练数据的CNN 网络,在经过大约50 个迭代周期后损失函数收敛至0 附近,均方根误差收敛至1 000 附近;而基于WVD 分布生成的时频数值矩阵作为训练数据的CNN 网络,在经过大约400个迭代周期后损失函数收敛至0附近,均方根误差收敛至1 000 附近.说明基于CWT 变换和STFT 变换生成的时频数值矩阵作为CNN 网络的训练数据更有利于CNN 网络的迭代收敛,有利于提高CNN网络的训练效率.
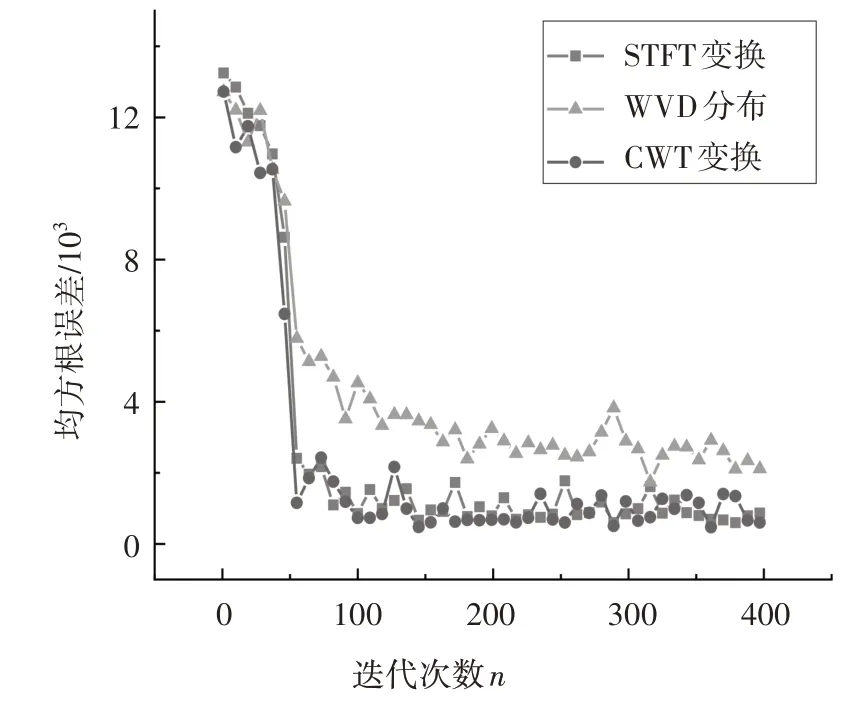
图12 损失函数Fig.12 Loss function
2.4.2 CNN网络对已训练荷载的识别结果
为验证CNN 网络对于已训练荷载的识别能力,首先,分别从荷载工况分组为2、4、6、12、14、16、…、38、40 t 数据里随机选取30 组数据,共计20×30=600组数据作为训练数据;再从每个荷载分组中余下的10 组数据中随机抽取2 组数据,共计20×2=40 组数据作为识别数据;其次,分别利用CWT变换、STFT变换、WVD 分布处理上述应变数据并生成大小为64×64 的数值矩阵,并将其作为CNN 网络的输入数据;最后,进行CNN 训练、识别及其误差计算,其识别结果如图13~图16 所示.可以看出,相比于STFT 变换和WVD 分布,基于CWT变换生成的时频数值矩阵作为训练数据的CNN网络,在识别已训练荷载值时的识别误差在±0.05%以内,说明基于CWT变换处理的应变信号更有利于CNN网络对已训练车辆荷载的识别.

图13 第1组数据荷载识别结果Fig.13 Load identification results of the 1st group of data

图14 第1组数据荷载识别误差Fig.14 Load identification error of the 1st group of data
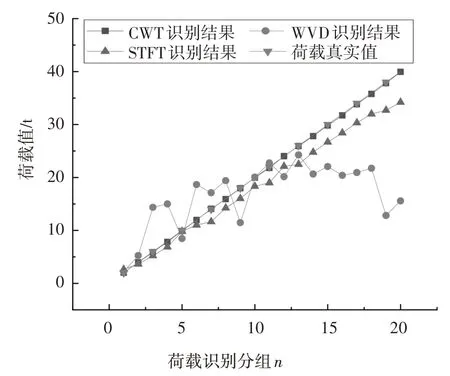
图15 第2组数据荷载识别结果Fig.15 Load identification results of the 2nd group of data

图16 第2组数据荷载识别误差Fig.16 Load identification error of the 2nd group of data
2.4.3 CNN网络未知荷载识别结果
本节采用上述表现较为优异的CWT 变换处理跨中应变数据,利用CNN网络的回归学习功能,在训练少量特定车辆荷载对应的应变信号时频数据后,直接建立起该数据与车辆荷载的映射关系,从而达到识别未知车辆荷载的目的.
首先,分别随机选取荷载工况分组为2、4、6、12、14、16 t 里的各40 组数据,共计6×40=240 组数据作为训练数据,同时分别随机选取荷载工况分组为8、10、18、20 t 里的各8 组数据,共计4×8=32 组数据作为识别数据;其次,利用CWT 变换处理上述应变数据并生成大小为64×64 的数值矩阵,并将其作为CNN 网络的输入数据;最后,为排除数据选择对训练识别精度造成的误差,本文进行了3 次识别数据的随机选择,并对CNN网络进行训练及识别验证,结果如图17~18所示.
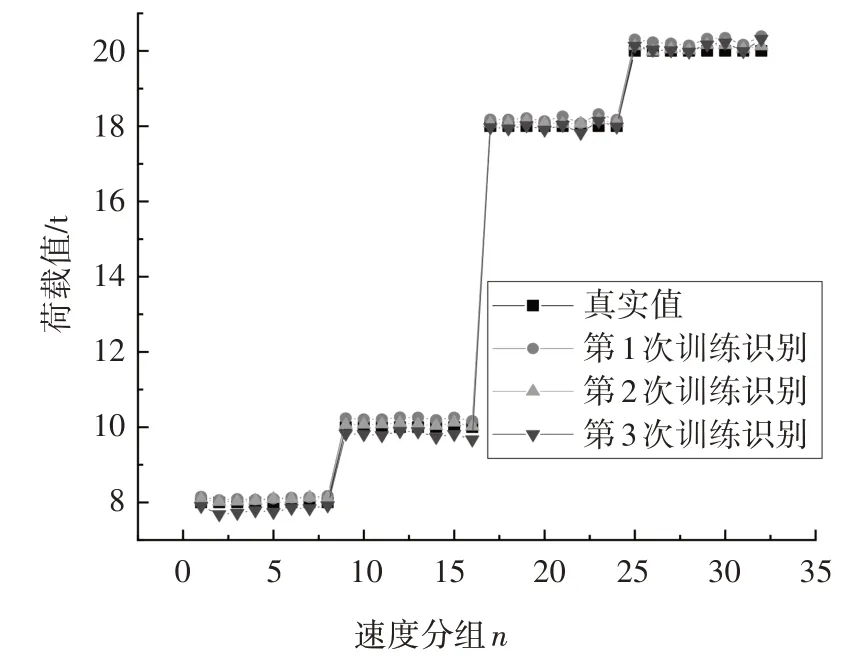
图17 车辆荷载识别结果Fig.17 Recognition of unknown vehicle weight
由图17 和图18 可知,在经过训练学习CWT 变换处理的应变信号数据后,该CNN 网络已具备识别未知荷载的能力,且该识别误差大部分在±4%以内,满足实际工程应用的要求.

图18 车辆荷载识别精度Fig.18 Recognition accuracy of unknown vehicle load
2.4.4 路面粗糙对CNN网络荷载识别的影响
由于不同的路面粗糙度会不同程度地影响车桥相互耦合振动的过程,因此为检验CNN 网络在不同路面粗糙度下对车辆荷载识别精度的影响,本文按照式(15)模拟了5 种不同等级的路面粗糙度,如图19所示,并用上述车桥耦合模型模拟了车辆以10 m/s 的速度在该路面粗糙度下行驶时桥梁跨中的应变响应.采用上文已训练的CNN 网络对该响应进行车辆荷载的识别,以检验其荷载识别精度,具体识别结果如图20和图21所示.

图19 路面粗糙度Fig.19 Road roughness

图20 不同路面粗糙度下的荷载识别结果Fig.20 Load identification results under different pavement roughness

图21 不同路面粗糙度下的荷载识别误差Fig.21 Load identification error under different pavement roughness
由以上识别结果可以看出,CNN 网络对于车辆在路面粗糙度等级为很好、好、中的桥梁上行驶时产生的桥梁跨中应变响应具有较好的荷载识别结果,其识别误差主要集中在-2%~5%的范围之内.随着路面粗糙度等级越差,其识别精度越低.
2.4.5 噪声对CNN网络荷载识别的影响
由于应变信号在采集过程中,环境和仪器自身会对信号产生一定的噪声影响,且这一影响因素难以消除,因此需要研究噪声对荷载识别精度的影响.在本小节中,首先,模拟信噪比为1 dB、5 dB 和10 dB的信号作为训练识别信号;其次,按照第2.4.2 小节的训练方案训练CNN 网络;最后,以车速为5 m/s 的信号作为识别信号检验CNN 网络的荷载识别精度,其识别结果如图22和图23所示.

图22 不同噪声影响下的荷载识别结果Fig.22 Load identification results under different noise effects
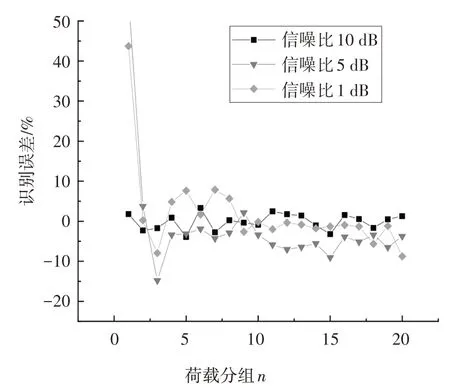
图23 不同噪声影响下的荷载识别误差Fig.23 Load identification error under different noise effects
由以上结果可以看出,噪声对荷载识别结果会有一定的影响.当信噪比为1 dB 和5 dB 时,识别误差较大,局部误差接近50%;当信噪比为10 dB时,噪声影响较小,误差基本在5%以下.
3 结论
本文提出了一种基于应变信号时频分析与CNN网络的车辆荷载识别方法,其具体步骤如下:首先,利用CWT 变换对应变响应进行时频分析获得时域信号的时频特征;其次,利用双线性插值算法处理该时频特征数据,生成大小为64×64 的数值矩阵作为CNN 网络的输入数据;最后,利用CNN 网络训练上述时频分析方法生成的数值矩阵进行车辆荷载的识别.同时,本文还比较了采用STFT 变换、WVD 分布以及CWT 变换处理的应变响应数据对CNN 网络训练识别效果的影响,以及对比了不同路面粗糙度和噪音影响下CNN 网络荷载识别的效果,最后得出以下结论:
1)相比于WVD 分布和STFT 变换,CWT 变换处理生成的应变信号时频数值矩阵更有利于提高CNN网络的荷载识别精度.
2)利用CNN 网络的回归学习功能,在进行少量样本学习后,便可建立输入数据与车辆荷载的映射关系,从而具备识别未知车辆荷载的能力,且具有较低的识别误差.
3)模拟了5 种随机路面粗糙度,并检验了CNN网络在不同路面粗糙度下的荷载识别情况,发现该CNN 网络荷载识别算法在前3 种路面粗糙度等级下,具有较高的荷载识别精度.
4)模拟了不同路面粗糙度和不同信噪比情况下,CNN 网络对于车辆荷载的识别精度,研究发现在前3 种路面粗糙度等级以及信噪比较高的情况下,CNN网络具有较高的荷载识别精度.
综上,本文提出的基于应变信号时频分析与CNN 网络的车辆荷载识别方法拥有较高的荷载识别精度,对于桥梁健康检测具有一定的参考价值.
