交错桁架钢框架结构抗震设计方法研究
2022-10-09周绪红周志彬周期石黄伟杨梦圆
周绪红,周志彬,周期石†,黄伟,杨梦圆
(1.中南大学土木工程学院,湖南长沙 410083;2.重庆大学土木工程学院,重庆 400045)
交错桁架钢框架结构体系由柱、钢桁架、纵向框架梁和楼板组成,因结构中包含较多的轴心受力构件,与传统框架结构体系相比,能更有效地发挥材料性能,使结构用钢量显著降低.交错桁架钢框架结构体系中的桁架可采用混合式桁架、空腹式桁架或帕式桁架等,其中混合式桁架由于结构刚度适中且建筑上能提供内廊,其应用最为广泛[1].
已有试验研究表明[2-5],混合式交错桁架钢框架结构在低周往复荷载作用下表现为斜腹杆失效的脆性破坏特征,抗震性能较差.如何改善混合式交错桁架结构抗震性能已成为近年来该结构的研究热点,改进思路主要有两种:一是在不改变传统桁架形式的基础上,将混合式桁架空腹节间的弦杆设置为耗能段,以提高结构的抗震性能.美国钢结构协会发布的交错桁架体系设计指南[6]中指出桁架空腹节间弦杆可以作为耗能构件,前提是需要保证斜腹杆一直处于弹性状态,但指南中未提出实现空腹节间弦杆耗能的设计计算方法.文献[7]基于能量平衡对交错桁架延性区段空腹节间弦杆进行了塑性设计,并采用传统桁架简化计算模型[6,8-9]对交错桁架的非延性区段构件进行弹性设计,由于传统桁架简化计算模型假定弦杆仅在空腹节间及与空腹节间相邻的节间连续、其余节间为铰接,其计算结果误差较大且此计算模型中受力最不利的腹杆即与空腹节间相邻的斜腹杆轴力计算值比真实值偏小;二是在传统交错桁架结构中增设耗能元件.如赵宝成等[10]在交错桁架中内填Y 形偏心腹杆,试验表明偏心腹杆式交错桁架滞回曲线比较饱满,结构的耗能能力较强.Kim等[11-12]提出了在交错桁架结构底层支撑和第2 层中部斜腹杆处设置防屈曲支撑或在桁架空腹节间设置摩擦阻尼器的方法,分析结果表明该方法能有效提高结构延性系数和极限层间位移角,降低结构的失效概率,增设耗能元件可有效提高交错桁架钢框架结构的抗震性能,但与空腹节间弦杆耗能结构相比,构造相对复杂.
在结构抗震设计中,为实现结构“大震不倒”的设防目标,一般采用弹塑性层间位移角限值确保结构在罕遇地震下的最大变形不超过其极限变形[13],与一般钢框架结构相比,交错桁架钢框架结构横向抗侧刚度大,弹塑性层间极限位移相对较小,一般钢框架结构的弹塑性层间位移角限值不适用于交错桁架钢框架结构.
为实现交错桁架钢框架结构延性破坏的设计目标以及“大震不倒”的抗震设防目标,本文基于空腹节间弦杆耗能的设计思路,采用更为精确的水平荷载作用下桁架杆件内力计算模型,推导桁架腹杆内力计算公式,建立桁架腹杆设计内力调整方法,并基于桁架弹塑性变形分析,提出交错桁架钢框架结构弹塑性层间位移角限值计算方法.
1 交错桁架钢框架结构破坏模式
在桁架方向水平地震作用下,交错桁架钢框架结构的层间剪力主要由钢桁架承受(见图1),一般可能出现两种不同的破坏机制(见图2):斜腹杆失效导致桁架丧失水平承载力进而引发整体破坏;桁架空腹节间弦杆截面转角达极限转角导致结构整体破坏.

图1 交错桁架钢框架结构Fig.1 Steel staggered truss framing systems
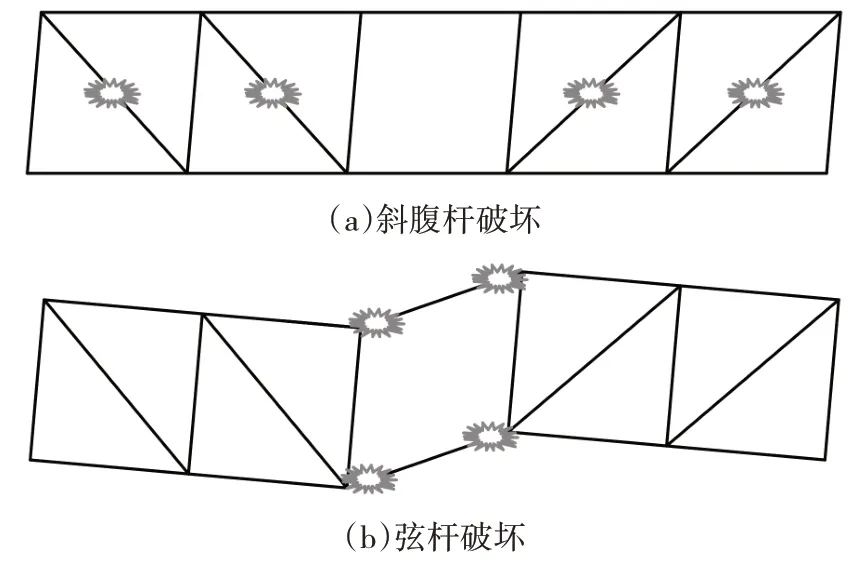
图2 交错桁架结构两种典型破坏模式Fig.2 Two typical failure modes of staggered truss structure
交错桁架钢框架结构中斜腹杆为轴心受力构件,屈曲后将迅速丧失承载力,因斜腹杆失效导致的结构整体破坏属脆性破坏.空腹节间弦杆在水平力下为受弯构件,在罕遇地震作用下构件端部形成塑性铰,可有效地耗散地震能量,提高结构的延性,因弦杆失效导致的结构整体破坏属延性破坏.因此,在交错桁架钢框架结构抗震设计中应避免斜腹杆屈曲,并使空腹节间弦杆出现塑性铰,以提高结构的耗能能力和延性.
2 桁架腹杆设计方法
交错桁架钢框架结构的抗震设计思路是使结构在罕遇地震作用下仅在桁架空腹节间弦杆处出现塑性铰,其余构件均不发生屈曲且保持弹性状态,即形成图2 中“弦杆破坏”的结构失效模式.为了实现这种理想的结构失效模式,需要对已满足“小震不坏”的桁架杆件进行设计内力调整,并使桁架斜腹杆在罕遇地震作用下不发生屈曲和保持弹性.
2.1 水平地震力下腹杆内力计算模型及方法
在水平地震力作用下,传统桁架简化计算模型[9]假定空腹节间及其相邻节间弦杆为连续,其余节间弦杆为铰接,计算较为简便.下文算例表明,传统桁架简化模型由于忽略了远离空腹节间弦杆的剪力和弯矩,导致腹杆轴力计算值偏差较大.
为了更准确地反映桁架杆件的实际受力状态,本文建议选取如图3(a)所示的弦杆完全连续的桁架内力计算模型,采用均布线荷载模拟地震作用下桁架所承受的水平力,根据桁架结构对称布置、荷载为反对称荷载的特点,可取图3(b)所示的隔离体进行内力分析.
分析图3(b)所示隔离体,并假定空腹节间上下弦杆所受剪力V相等[6,8],根据力矩平衡可知其剪力V为:
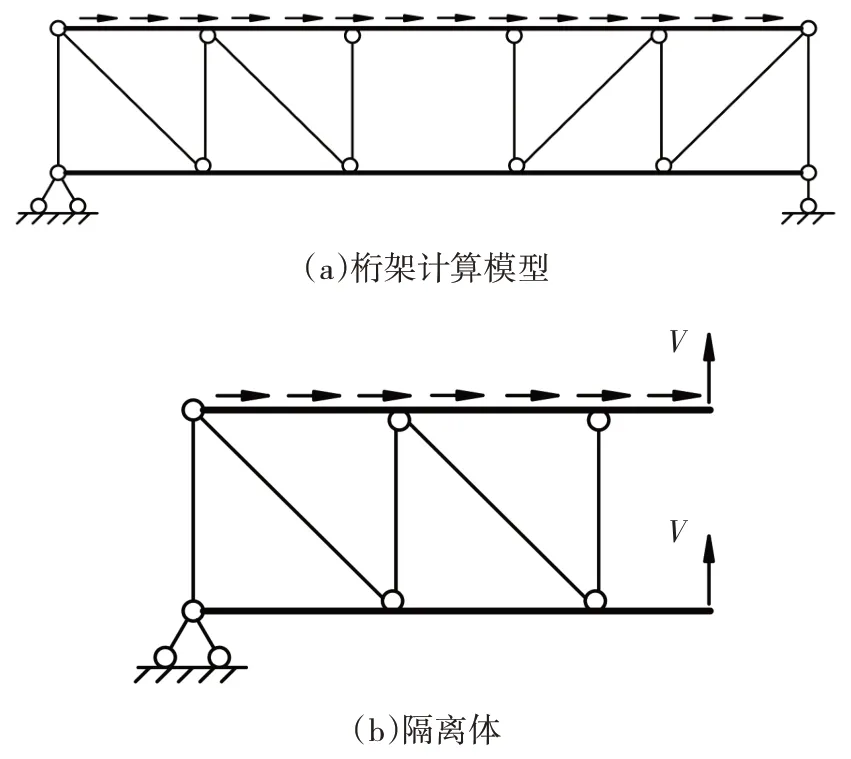
图3 本文建议的水平力作用下桁架内力计算模型Fig.3 The calculation model of truss internal force under horizontal force suggested in this paper

式中:h为桁架高度;L为桁架长度;F为桁架所承受的水平力.
将上下弦杆等效为两根带悬臂的连续梁,可得上下弦杆弯矩图和剪力图如图4 所示,图中,Lw为桁架带斜腹杆节间长度,Lv为空腹节间长度.

图4 桁架弦杆内力图Fig.4 Internal force diagram of chord members
根据弦杆等效连续梁模型求得的各支点反力可以反算得到腹杆轴力如图5 所示,图中,α为斜腹杆与水平面夹角.
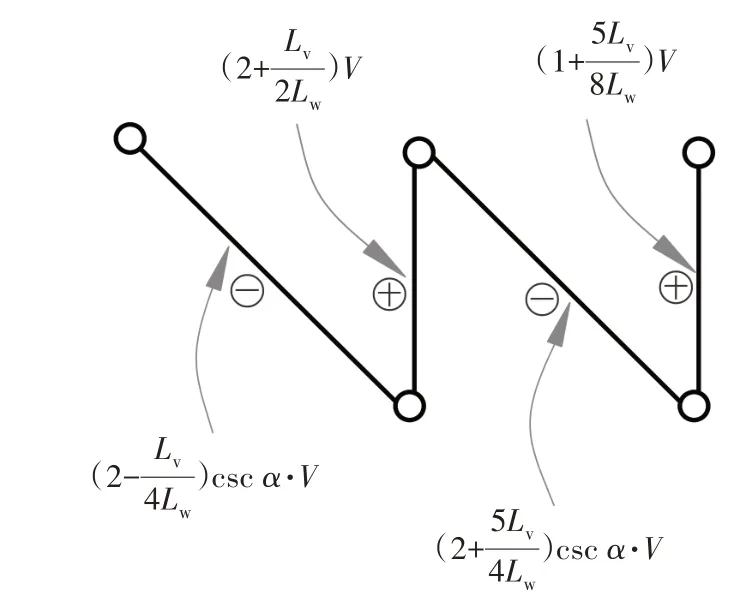
图5 左半桁架腹杆轴力Fig.5 Axial force of web members of left half truss
从图5 中可看出,水平力并非按斜腹杆刚度分配到每根斜腹杆,这是由于桁架上下弦杆并非刚体,空腹节间及靠近空腹节间的弦杆弯曲变形相对较大,因此,靠近空腹节间的斜腹杆受力明显大于远离空腹节间的斜腹杆.
为验证图5 所示腹杆计算公式的准确性,采用有限元软件SAP2000 建立了一榀桁架的有限元模型.桁架跨度为15 m,所有节间长度均为3 m,各构件的截面尺寸见表1,楼板跨度6 m,厚度为120 mm.桁架下弦杆与楼板通过节点相连,并约束楼板的位移UX和UZ,模拟楼板的支承;在桁架上弦杆端部约束Y向位移模拟上层楼板对桁架的侧向支承,并在桁架柱脚处约束竖向和Y向位移,具体边界条件如图6所示.上层楼板传来的水平力以均布线荷载的形式施加在桁架上弦杆,在桁架上弦杆施加合力为1 000 kN的均布线荷载.图6 中①号、②号、③号和④号腹杆轴力的传统桁架简化计算模型分析结果、按本文式(1)和图5中公式计算结果及有限元分析结果见表2.

表1 桁架截面尺寸Tab.1 Sections and dimensions of members of truss
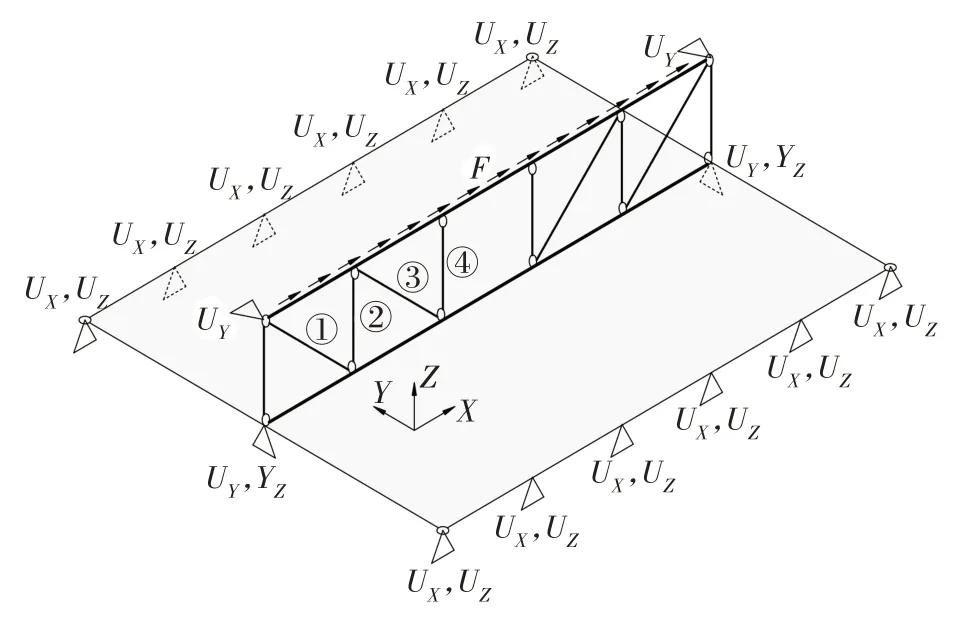
图6 有限元模型示意图Fig.6 Schematic diagram of finite element model
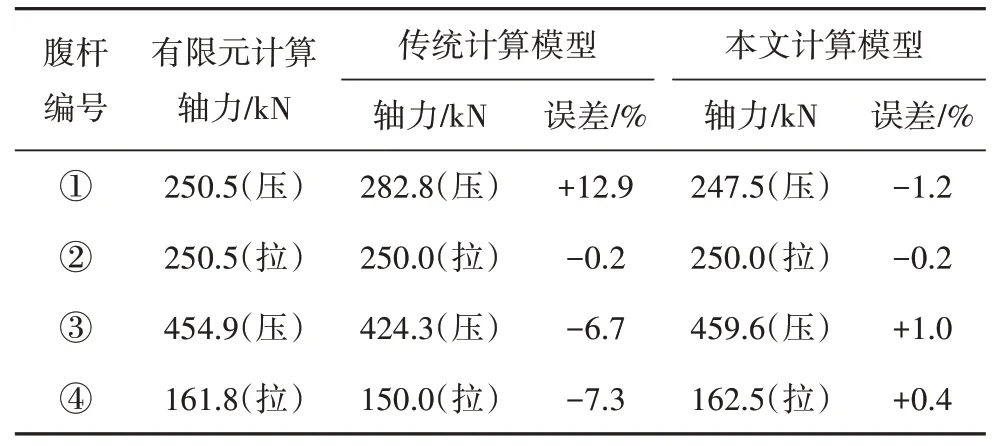
表2 腹杆轴力计算结果对比Tab.2 Comparison of axial force calculation results of web members
从表2 中可看出,按传统桁架简化计算模型得到的腹杆轴力误差较大,且受力最不利的③号斜腹杆轴力计算结果小于有限元分析结果.本文提出腹杆内力的计算模型及推导的计算公式计算结果与有限元分析结果更为接近,且受力最大的斜腹杆计算轴力略高于有限元分析结果,满足工程精度的同时使结构偏于安全.
2.2 腹杆设计内力调整方法
为实现交错桁架钢框架结构“强腹杆弱弦杆”的设计原则,需要对小震作用下桁架腹杆的计算内力进行调整,以保证在罕遇地震作用下空腹节间弦杆先于斜腹杆发生破坏.
当桁架空腹节间弦杆在罕遇地震作用下产生塑性铰时,若不考虑塑性铰强化,可以认为此时桁架水平承载力达到最大,同时空腹节间弦杆剪力V也达到最大剪力Vp:

式中:Lvn为桁架空腹节间弦杆净跨度;Mp为空腹节间弦杆的塑性铰弯矩,可参考我国《高层民用建筑钢结构技术规程》(JGJ 99—2015)[14]对偏心支撑耗能梁段承载力的规定取为全塑性受弯承载力.

式中:Wp为弦杆对其水平轴的塑性净截面模量;f为钢材强度设计值.当楼板与弦杆组合效应不可忽略时,计算Mp还需考虑弦杆-楼板组合效应的放大作用,可参考《高层民用建筑钢结构技术规程》(JGJ 99—2015)[14]中对两侧带楼板框架梁的规定取放大系数为1.5.
将Vp代入图5 所示腹杆轴力计算公式,并对腹杆轴力与重力荷载代表值作用下的腹杆轴力进行组合,得到调整后的腹杆轴力设计值Nw,com为:

式中:Nw,E为弦杆产生塑性铰时按图5所示轴力公式计算的腹杆轴力;Nw,G为重力荷载代表值作用下的腹杆轴力;ηw为腹杆内力设计值增大系数,主要考虑的是弦杆塑性铰区钢材强化,可参考现行规范对偏心支撑内力设计值增大系数的规定[14],根据建筑结构的抗震等级确定;γG为重力荷载分项系数,当重力荷载效应对构件不利时取1.0,重力荷载效应对构件有利时可取小于1.0.
考虑到不同荷载组合下,腹杆内力可能出现大于Nw,com的情况,将Nw,com与按现行规范基于极限状态法设计的构件内力设计值进行比较,选取更为不利的设计值作为最终设计值进行构件截面设计.
3 层间位移角限值
3.1 弹性层间位移角限值
我国《建筑抗震设计规范》(GB 50011—2010)[13]规定:在多遇地震作用下,建筑主体结构应不受损坏,非结构构件没有过重破坏并导致人员伤亡,保证建筑的正常使用功能.其中保证建筑的正常使用功能主要包括控制混凝土剪力墙、柱等重要抗侧力构件的开裂[15].对于交错桁架钢框架结构而言,混凝土楼板作为竖向承重和水平传力构件一般按照不出现斜裂缝的深梁设计[9,16],因此交错桁架钢框架结构仅需要通过变形控制非结构构件的损坏即可,参考现行《建筑抗震设计规范》(GB 50011—2010)[13]弹性层间位移角限值可取1/250.
3.2 弹塑性层间位移角限值
结构的整体倒塌或局部倒塌,往往是由于个别主要抗侧力构件在强烈地震下的最大变形超过其极限变形能力所造成的,因此,在抗震设计时应进行罕遇地震作用下的结构弹塑性变形验算.《建筑抗震设计规范》(GB 50011—2010)[13]规定了多种常用钢结构体系的弹塑性层间位移角限值为1/50,但并不适用于交错桁架钢框架结构体系.
根据前述交错桁架钢框架结构的设计原则,在罕遇地震作用下结构仅在空腹节间弦杆处出现塑性铰,其余构件均不发生屈服或保持弹性状态,所以交错桁架结构塑性层间位移角仅由空腹节间弦杆塑性变形引起.因此可以将结构在罕遇地震作用下的弹塑性层间位移角分为弹性层间位移角和塑性层间位移角两部分,即楼层弹塑性层间位移角θ为:

式中:θe为楼层弹性层间位移角;θp为楼层塑性层间位移角.
楼层弹性层间位移角θe根据其组成性质可分为结构整体弹性弯曲变形引起的层间位移角和楼层弹性剪切变形引起的层间位移角,即弹性层间位移角θe为:

式中:θf为结构整体弹性弯曲变形引起层间位移角;θs为楼层弹性剪切层间位移角.我国《建筑抗震设计规范》(GB 50011—2010)[13]指出对于高度大于150 m的结构,计算层间位移角时可以考虑结构整体弯曲变形所产生的影响,而交错桁架结构目前仅推荐用于100 m及以下结构,故本文计算弹塑性层间位移角限值时偏安全地不考虑交错桁架结构的整体弯曲变形,即楼层弹性层间位移角为:

楼层弹性剪切位移角θs主要由桁架斜腹杆轴向弹性变形和空腹节间弦杆弹性弯曲变形引起,即楼层弹性剪切位移角θs为:

式中:θs1为桁架斜腹杆轴向弹性变形引起的楼层剪切位移角;θs2为桁架空腹节间弦杆弹性弯曲变形引起的楼层剪切位移角,如图7 所示,图中γe为空腹节间弦杆弹性弯曲转角.
根据图7,由几何关系可得斜腹杆轴向弹性变形引起的弹性层间位移角θs1和空腹节间弦杆弯曲弹性变形引起的弹性层间位移角θs2分别为:

图7 楼层弹性剪切变形Fig.7 Elastic shear deformation of storey

式中:ε为斜腹杆的平均应变;α为斜腹杆与水平面夹角;L为桁架全长;Lv为桁架空腹节间长度.
桁架空腹节间弦杆端部形成塑性铰时的塑性变形如图8 所示.根据几何关系,楼层塑性层间位移角θp为:
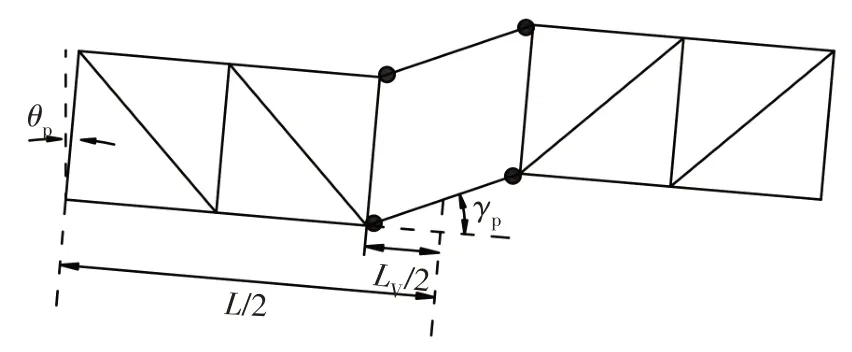
图8 桁架塑性变形图Fig.8 Plastic deformation diagram of truss

式中:γp为弦杆塑性转角.
综合式(5)、式(7)~式(11)可得楼层弹塑性层间位移角θ为:

由式(9)可知,在桁架布置形式确定的情况下,斜腹杆轴向弹性变形引起的楼层剪切位移角θs1的大小取决于斜腹杆平均应变ε的大小.桁架斜腹杆在水平力作用下处于受压或者受拉状态,其中斜腹杆受压时承载力由稳定控制,其弹性极限变形量低于受拉斜腹杆,所以桁架斜腹杆轴向弹性变形引起的楼层剪切位移限值[θs1]取决于受压斜腹杆的弹性变形能力.规范[9]推荐的斜腹杆截面形式为方钢管,因此选取几组斜腹杆常用的方钢管截面,并根据规范计算其达到受压承载力设计值时斜腹杆的平均应变ε作为斜腹杆的平均应变限值[ε],见表3.
由表3可知,不同斜腹杆截面设计平均应变ε介于0.001 0~0.001 2 之间,可偏安全地取0.001 0 作为斜腹杆的平均应变限值[ε].

表3 常用桁架斜腹杆设计平均应变Tab.3 Design average strains of diagonal web member of comon truss
桁架斜腹杆与水平面夹角α一般为30°~60°之间[9],因此csc2α介于1~1.15 之间,可偏安全地取1作为csc2α的限值,对应桁架斜腹杆与水平面夹角α为45°.
参考ASCE/SEI 41—17[17]中考虑剪切变形的梁屈服转角的计算方法,空腹节间弦杆弹性弯曲转角限值[γe]可取为:
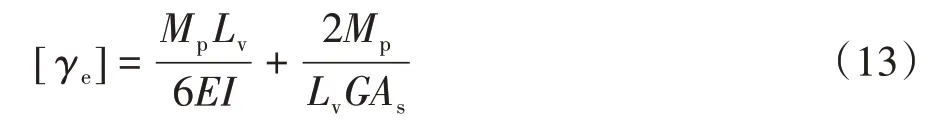
式中:As为弦杆腹板面积.
规范[9]推荐的桁架弦杆截面形式为宽翼缘H 型钢,选取几组桁架弦杆常用的宽翼缘H 型钢截面,根据式(13)计算的桁架弦杆屈服转角见表4.

表4 常用桁架弦杆屈服转角Tab.4 Yield rotation angles of chord member of comon truss
由表4 可知,常用弦杆截面屈服转角为0.008~0.010 rad,可偏安全地取0.008 rad作为弦杆弹性弯曲转角限值[γe].
从式(11)中可看出,在桁架布置形式确定的情况下,空腹节间弦杆的塑性转动能力越大,楼层可承受的塑性层间位移角也越大,弦杆的延性决定了整个桁架的延性.关于交错桁架弦杆塑性转角限值[γp]的试验研究较少,参考钢框架梁端塑性转角的试验研究[18-23]可知,满足一定构造措施的钢梁均能表现出优秀的塑性转动能力.本文参考美国钢结构抗震设计规范ANSI/AISC 341—2016[24]中对特殊抗弯框架的规定,取弦杆塑性转角限值[γp]为0.04 rad.
综上可知,桁架斜腹杆的平均应变限值[ε]可取0.001,桁架斜腹杆与水平面夹角α取为45°,桁架空腹节间弦杆弹性弯曲转角限值[γe]可取0.008 rad,弦杆塑性转角限值[γp]取0.04 rad.根据式(12)可得桁架弹塑性层间位移角限值[θ]为:
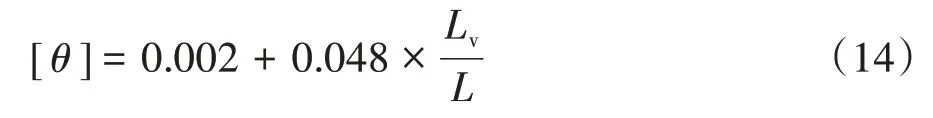
以层高3 m,带斜腹杆节间距均为3 m 的桁架为例,根据式(14)计算出不同空腹节间距的5 节间桁架弹塑性层间位移角限值见表5.
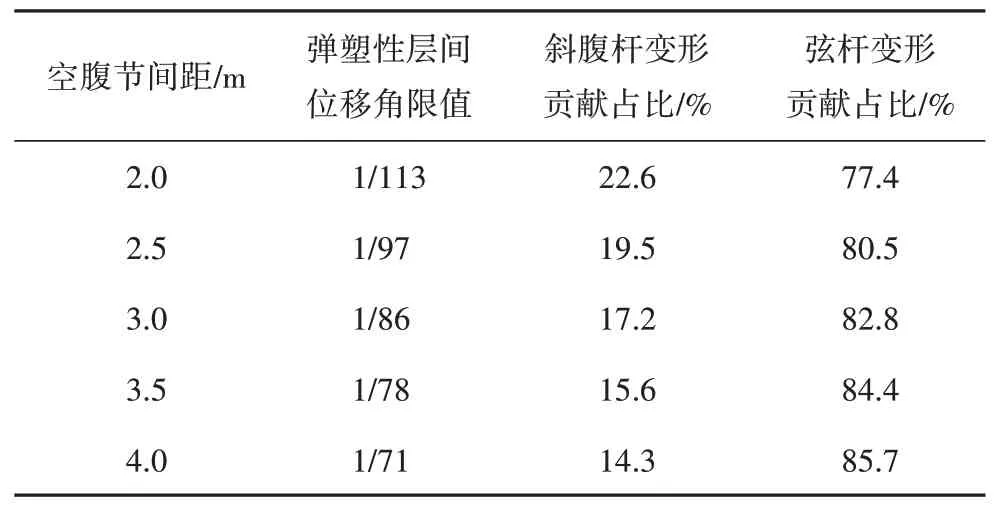
表5 不同空腹节间距结构弹塑性层间位移角限值Tab.5 Limit value of elastoplasticity inter-storey drift ratio under different lengths of vierendeel panels
从式(14)和表5 可知,斜腹杆弹性变形对交错桁架钢框架结构弹塑性层间位移角限值的贡献为0.002 rad;而弦杆弹塑性变形的贡献随着空腹节间距与桁架全长比值的增大而增大,且占主要部分;交错桁架钢框架结构弹塑性层间位移角限值小于现行《建筑抗震设计规范》(GB 50011—2010)[13]规定的多层和高层钢结构房屋的弹塑性层间位移角限值(1/50),故交错桁架钢框架结构设计时需要根据桁架布置情况选择相应的弹塑性层间位移角限值.
4 算例分析
4.1 结构设计
基于上述腹杆内力调整方法和弹塑性层间位移角限值规定,提出一种交错桁架钢框架结构抗震设计方法,其设计流程见图9.
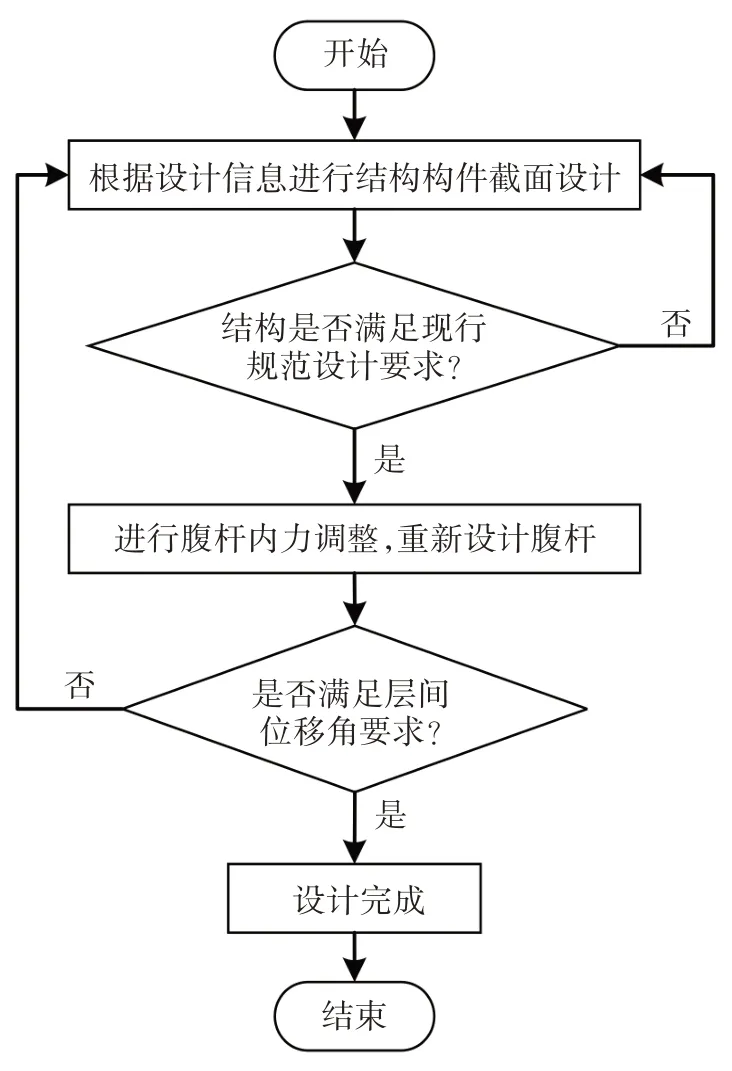
图9 交错桁架钢框架结构抗震设计流程图Fig.9 Seismic design flow chart of steel staggered truss framing systems
为验证本文抗震设计方法的合理性,运用结构设计软件PKPM,按现行规范设计了一栋交错桁架钢框架结构SST1,同时按本文提出的抗震设计方法设计了一栋交错桁架钢框架结构SST2.结构布置如图10 和图11 所示,荷载信息为:楼屋面恒载(含楼板自重)为5 kN/m2,楼屋面活载为2 kN/m2,抗震设防烈度为8 度(0.2g),设计地震分组为第二组,场地类别为Ⅱ类.

图10 结构平面布置图Fig.10 Structural plan

图11 结构立面图Fig.11 Structural elevation
SST1 和SST2 构件截面尺寸见表6.SST1 和SST2的钢柱、底层支撑、弦杆截面尺寸相同,腹杆截面尺寸不同,钢材选用Q345,混凝土楼板厚度均为120 mm,混凝土强度均为C30.其中,SST2 腹杆内力调整时,腹杆内力设计值增大系数ηw取为1.3;计算弦杆塑性铰弯矩Mp时,弦杆-楼板组合效应的放大系数取为1.5.

表6 结构构件截面尺寸Tab.6 Sections and dimensions of structural members
4.2 罕遇地震下结构弹塑性时程分析
为了评估所设计的模型SST1 和SST2 的抗震性能,运用有限元软件SAP2000 对其分别进行了弹塑性时程分析,其中结构阻尼比取值为0.05,根据2.2节分析,模型中弦杆刚度放大系数取为1.5.
4.2.1 地震波的选取
根据我国抗震规范及有关研究的建议[13,25],地震波的选取需满足地震动幅值、持时和频谱特性的要求,即8 度(0.2g)罕遇地震波峰值加速度(Peek Ground Acceleration,PGA)取400 gal;地震动有效持时需大于结构基本周期的5 倍;地震记录反应谱与规范反应谱在平台段和结构基本周期附近均值相差不超过10%.模型SST1和SST2计算所得的横向基本自振周期分别为1.84 s 和1.73 s,从太平洋地震工程研究中心数据库(PEER ground motion database)中筛选出地震动有效持时(D5-95)大于9.2 s 的地震动记录,根据频谱特征选择10 条地震波并将每条地震波PGA 缩放到400 gal,所选地震波信息及频谱特性如表7和图12所示.
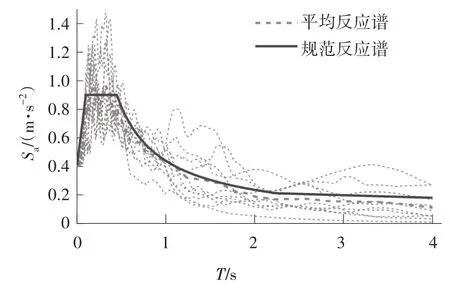
图12 地震波反应谱Fig.12 Response spectrum of seismic records
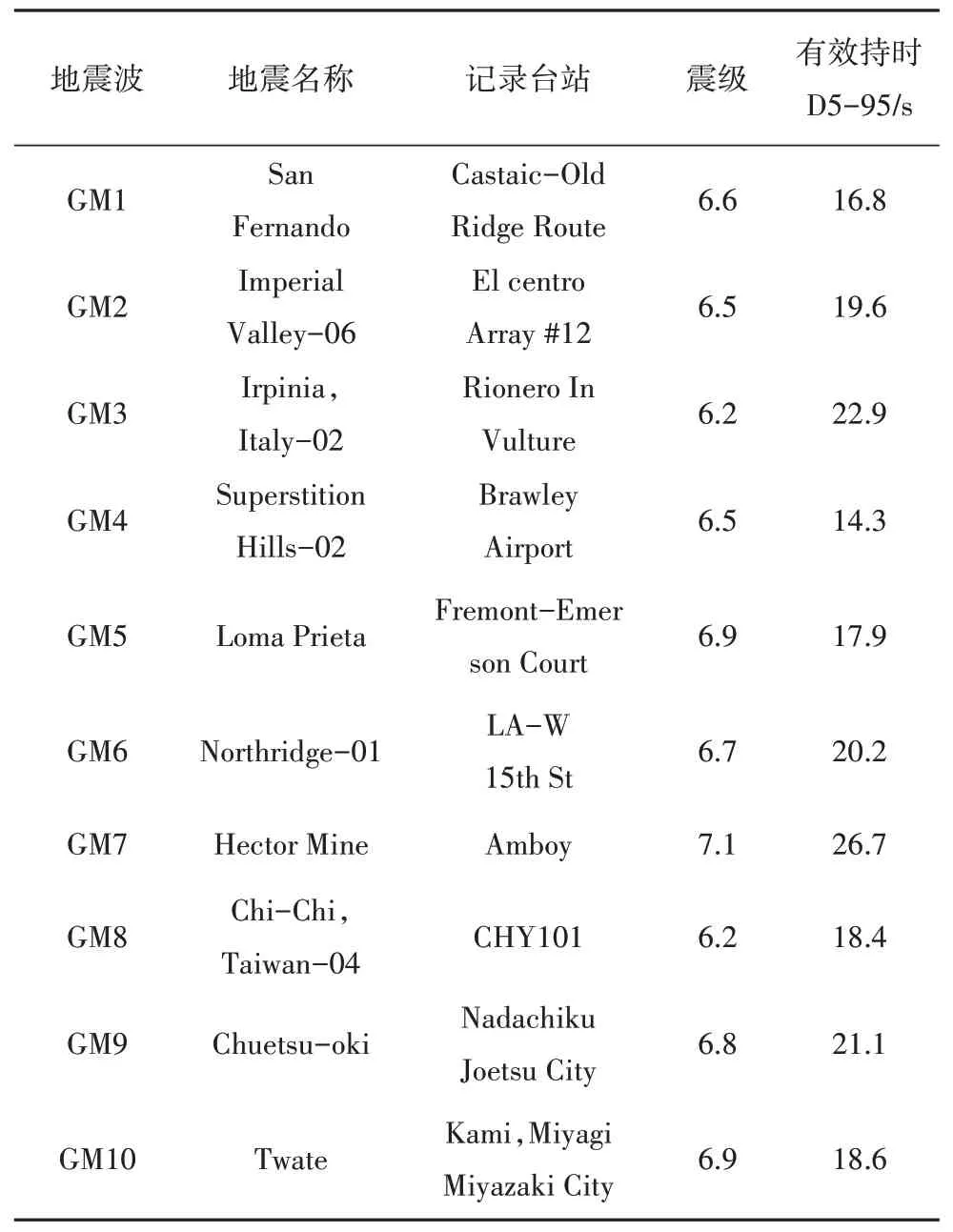
表7 地震波信息Tab.7 Information of seismic records
4.2.2 构件损伤状态及性能水准定义
SAP2000 采用集中塑性铰模型表征构件的弹塑性性能及损伤状态,塑性铰为钢塑性,无弹性行为,杆件其余部分保持弹性.算例中的柱采用P-M2-M3铰,桁架弦杆采用弯曲铰,桁架腹杆采用轴力铰,并在动力时程分析时采用程序默认的等向强化滞回准则.图13为弯曲铰非线性力-变形关系示意图.

图13 弯曲铰非线性力-变形关系曲线Fig.13 Nonlinear force-displacement relationship of moment hinge
图13 中,B 为屈服点;C 为破坏点,即构件达到承载力极限状态;D为倒塌点;E为最大变形点.基于构件内力与宏观变形关系,构件性能水准包含立即使用(IO)、生命安全(LS)、接近倒塌(CP)三个性能点.
塑性铰参数及各性能目标对应的变形限值大小取决于构件截面宽厚比和柱轴力等因素,参照ASCE/SEI 41—17[17]中表9-6、表9-7 所推荐的数值,本算例中弦杆性能目标与变形值的对应关系见表8.
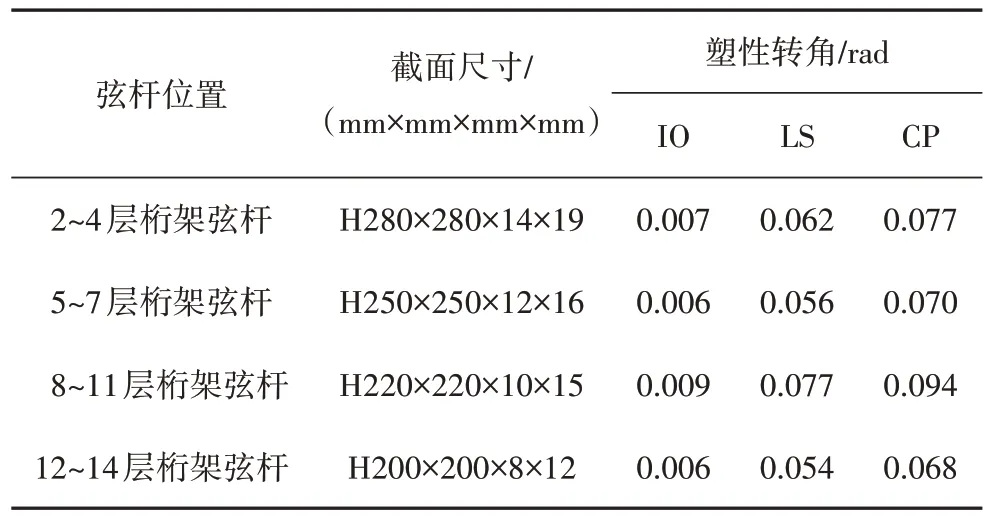
表8 弦杆各性能水准塑性转角Tab.8 Plastic rotation of chord member under different performance levels
4.2.3 地震响应分析结果
通过对模型SST1和SST2进行8度(0.2g)罕遇地震下的弹塑性时程分析,在地震波GM2 作用下结构的损伤最为严重,限于篇幅,本文仅以地震波GM2波作用下的结构响应为例进行对比分析.GM2 波作用下结构顶点位移-时程曲线,如图14所示.
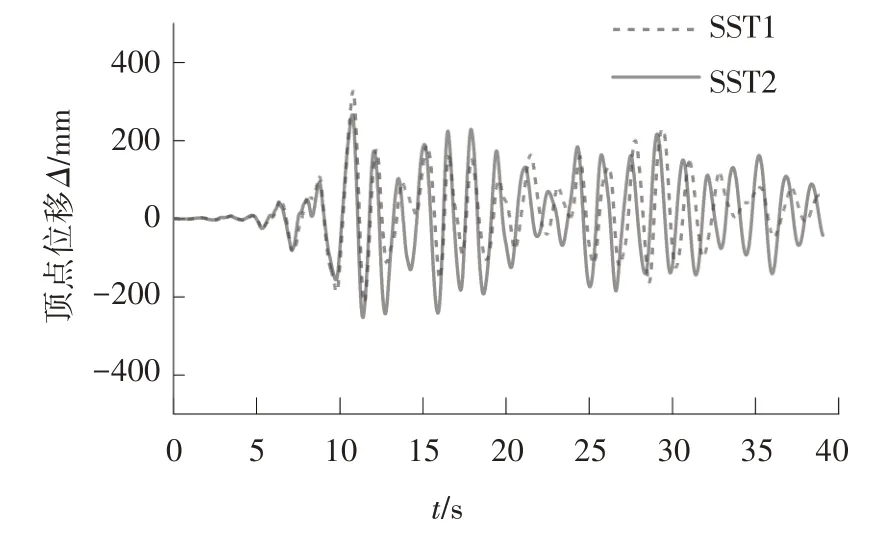
图14 顶点位移-时程曲线Fig.14 Time history curve of roof displacement
从图14可知,SST1模型最大顶点位移大于SST2模型.SST2 模型顶点最大位移出现在10.76 s 时,为265 mm.此时,结构整体变形近似于结构在桁架向的一阶振型,桁架两侧柱顶点高差为20 mm,计算可得此时结构整体弯曲引起的顶层层间位移角θf14为0.001 3 rad.由于θf随着楼层高度增加而增大,即其他楼层θf均小于0.001 3 rad,远小于楼层总体层间位移角,可忽略结构整体弯曲对层间位移角的贡献,说明此算例结构变形模式属剪切型,也证明了上文提到的“结构整体弯曲变形对层间位移影响相对较小”的结论.
图15 给出了弹塑性时程分析得出的楼层最大层间位移角包络曲线,SST2 模型各层层间位移角分布较为均匀,无明显薄弱层,最大层间位移角出现在第9 层,为1/94,小于上节所得到的限值要求(1/86),结构底层由于并未布置桁架,其层间位移角限值可按照钢框架结构控制(1/50).SST1 模型最大层间位移角出现在第2 层,为1/74,底部楼层层间位移角显著大于中上部楼层,这是由于2 层、3 层部分桁架斜腹杆在罕遇地震下产生严重损伤,导致了楼层抗侧刚度发生严重退化,形成薄弱层.

图15 层间位移角包络曲线Fig.15 Envelope curve of inter-storey drift ratio
SST1 和SST2 结构典型榀塑性铰分布情况如图16~17 所示.从图16 中可知基于传统极限状态法设计的SST1 结构由于未经设计内力调整,其部分斜腹杆出现塑性铰,且2~3 层部分斜腹杆由于变形过大已经发生严重损伤,超出CP(接近倒塌)性能点,结构难以保证“大震不倒”的设计目标;而图17 中按照本文所述方法设计的SST2结构在罕遇地震作用下,斜腹杆始终处于弹性状态,弦杆塑性铰发展充分,能够较为良好地耗散地震能量,结构整体可以实现“大震不倒”的设计目标.

图16 SST1典型榀最终塑性铰分布Fig.16 Plastic hinge formation in SST1

图17 SST2典型榀最终塑性铰分布Fig.17 Plastic hinge formation in SST2
5 结论
1)基于桁架空腹节间弦杆破坏的结构失效模式,提出了水平力作用下桁架杆件内力计算模型及罕遇地震作用下桁架腹杆内力的调整方法.
2)基于桁架弦杆失效的结构失效模式和桁架的极限变形,提出了不同空腹节间距下结构的弹塑性层间位移角限值.
3)提出了一种交错桁架钢框架结构抗震设计方法及流程.算例分析表明,采用本文方法设计的交错桁架钢框架结构能有效耗散地震能量,实现“强腹杆弱弦杆”和“大震不倒”的设计目标.
