钢筋桁架楼承板-U 形钢组合梁不同抗剪连接方式的受弯性能

胥兴，程睿，2†，刘吉春，崔佳，2，黄宗明，2

（1.重庆大学土木工程学院，重庆 400045；2.山地城镇建设与新技术教育部重点实验室（重庆大学），重庆 400045）

U 形钢-混凝土组合梁（U 形梁）是指在U 形钢内部和上部浇筑混凝土形成肋部混凝土和翼板混凝土，依靠钢和混凝土间的界面粘结力和抗剪连接件的作用形成的能共同工作的新型组合梁［1］.抗剪连接件是保证U 形钢与翼板混凝土共同工作的关键，传统的H 型钢-混凝土组合梁主要使用栓钉、角钢、槽钢等作为抗剪连接件，但对于U 形梁这一新型组合构件，不同抗剪连接件的形式、布置方式、抗剪性能等对其受力性能都有一定影响.

Oehlers 等［2-3］对U 形梁进行了抗弯和抗剪性能试验研究，分析了其弯曲破坏和剪切破坏两种破坏形态，试验结果表明：U 形钢和肋部混凝土的相对滑移在达到极限荷载附近时才会出现.Hanaor等［4］提出了采用“预埋式”和“自攻式”两种抗剪连接方式的U形梁，设计了推出试验来研究这两种抗剪连接方式的抗剪连接性能，结果表明两种抗剪连接方式的试件均具有较好的延性和较高的承载力.芬兰的Rautaruukki 公司申请了U 形梁的专利并对其进行推广应用，但其抗剪连接件的设计借鉴了Eurocode 4［5］对传统抗剪连接件设计的有关条文，并未考虑U 形梁的真实受力特点.林于东等［6］对12 根采用栓钉作为抗剪连接件的翼缘外翻U 形梁进行了静力试验研究，试验结果表明：U 形梁在受弯时基本满足平截面假定，且肋部混凝土可以延缓U 形钢侧板屈曲，使得组合梁刚度得到提高.周天华等［7］对3根使用角钢作为抗剪连接件的U 形梁进行了静力试验研究，结果表明：即使在角钢连接件设置不足时，U 形梁仍然表现出良好的延性和较高的承载力.李爱群等［8-11］对U形梁进行了较系统的研究，其设计的U 形梁使用底板栓钉、翼缘栓钉和构造钢筋作为抗剪连接件，栓钉数量多且焊接工作量大，工程应用具有一定困难.张婷［12］对两种采用不同抗剪连接方式的U 形梁进行了系统的研究及理论分析，一种是翼缘栓钉加内隔板，一种是翼缘角钢，结果表明翼缘栓钉加内隔板试件的混凝土与钢板间粘结性能优于翼缘角钢.郭兰慧等［13］对采用角钢作为抗剪连接件的翼缘外翻U 形梁的抗剪连接性能进行了研究，结果表明将角钢焊接于U 形钢翼缘的试件延性较好，而将角钢焊接于U形钢腹板的试件则发生脆性破坏.除U 形梁外，部分学者还对采用不同连接形式的其他组合梁的抗剪连接性能进行研究，包括胶合竹-混凝土组合梁［14］和冷弯薄壁型钢-细石混凝土组合梁［15］等.

以上研究均采用传统的栓钉或角钢等抗剪连接件，施工时焊接量较大且成本高，同时也影响楼板钢筋的绑扎，不利于在U 形梁中推广使用，因此本文将应用广泛的金属底模钢筋桁架楼承板的下弦钢筋焊接于U 形钢上翼缘作为一种新型抗剪连接件，并与传统的栓钉、角钢抗剪连接件进行组合，以研究不同抗剪连接件及其布置方式对U 形梁受弯性能的影响.主要研究内容如下：对4 根采用不同抗剪连接件的简支U 形梁进行受弯性能试验研究和有限元分析，得出U 形梁的破坏形态，分析比较采用不同抗剪连接方式的U 形梁的受弯性能和纵向受剪连接性能，根据全截面塑性理论提出了受弯承载力计算公式，研究结果为该类型组合梁的设计及应用提供依据.

1 试验概况

1.1 试件设计

共设计了4 个采用不同抗剪连接方式的试件，即钢筋桁架（UXL1-T）、钢筋桁架+栓钉（UXL2-（T+S））、钢筋桁架+角钢（UXL3-（T+A））和栓钉（UXL4-S）.试件总高为300 mm，有效加载长度为2.7 m；楼承板型号为TD2-70，栓钉直径为13 mm，高65 mm；角钢型号为45 mm×5 mm，长度为120 mm.

表1 试件主要参数Tab.1 Parameters of specimens

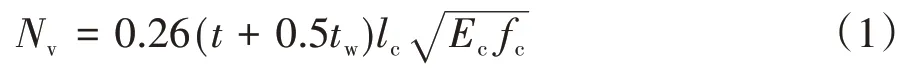
式中：t为角钢下翼缘厚度的一半；tw为角钢腹板的厚度；lc为角钢的长度.以试件UXL4-S 为例，其构造和详细尺寸如图1所示.

图1 试件UXL4-S构造（单位：mm）Fig.1 Details of specimen UXL4-S（unit：mm）

1.2 材性试验

试件钢材等级为Q355B，钢筋等级为HRB400，根据《金属材料拉伸试验第1 部分：室温试验方法》（GB/T 228.1—2010）［17］，每种厚度的钢材和每种直径的钢筋分别取3 块拉伸试样，其材料特性平均值见表2.混凝土采用C35 自拌混凝土，按照《混凝土物理力学性能试验方法标准》（GB/T 50081—2019）［18］，取每组3 个试块，测得其立方体抗压强度fcu为36 MPa，轴心抗压强度fc为24 MPa，弹性模量Ec为31.6 GPa.

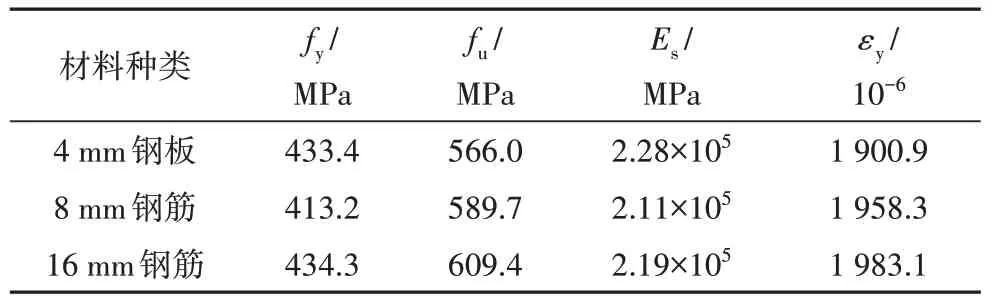
表2 钢材材料特性Tab.2 Mechanical properties of steel

1.3 加载和测量

试验采用三等分点加载，加载装置如图2 所示.试件屈服前按照20 kN的级差加载，达到屈服荷载后持续加载至构件发生破坏，即荷载下降到极限荷载的85%或变形过大而不适于继续加载.试验测量方案和应变片布置情况如图3 所示，测量包括端部U形钢与翼板混凝土的相对滑移（DT1 和DT3）、端部U 形钢与肋部混凝土的相对滑移（DT2 和DT4）、支座沉降（DT5 和DT6）、跨中和加载点挠度（DT7、DT8和DT9）.

图2 加载装置Fig.2 Test setup

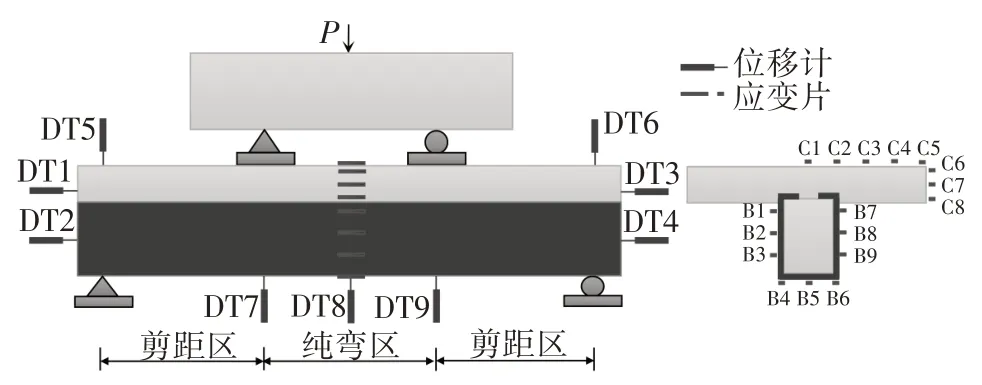
图3 试验装置及测量方案Fig.3 Test setup and measuring scheme

2 试验现象及结果分析

2.1 试验现象及破坏形态

2.1.1 试件UXL1-T和试件UXL3-（T+A）

试件UXL1-T 和试件UXL3-（T+A）的试验现象类似，在加载初期无明显现象；当加载到0.5Pu左右时，由于钢筋桁架楼承板的金属底模与翼板混凝土变形不协调，故在加载点附近率先脱开（图4（a）），同时由于角钢等抗剪连接件的劈裂作用，试件在剪跨区板顶出现一条较小的纵向裂缝（图4（b））；当加载到0.7Pu左右时，试件的跨中挠度明显增大，翼板混凝土侧面出现由下到上的裂缝，并逐渐向上发展（图4（c））；加载到Pu之后，加载点处的翼板混凝土被压溃，并开始脱落致使承载力下降（图4（d）），同时试件端部的颈部混凝土被剪断（图4（e）），导致U 形钢与翼板混凝土的相对滑移值逐渐增大，也表现出一定掀起变形，说明其抗剪连接性能不足.

图4 试件破坏特征Fig.4 Failure modes of the specimens

2.1.2 试件UXL2-（T+S）和试件UXL4-S

对于试件UXL2-（T+S）和试件UXL4-S，在达到极限承载力时，端部的U 形钢与翼板混凝土的相对滑移值较小，未出现掀起变形，发生与钢筋混凝土适筋梁类似的弯曲破坏（图4（f）），说明其抗剪连接性能良好.

2.2 P-δ曲线

各试件的荷载P-跨中挠度δ曲线见图5，可知试件UXL2-（T+S）和试件UXL4-S 的承载力和刚度明显大于试件UXL1-T和试件UXL3-（T+A），说明采用钢筋桁架和钢筋桁架与角钢作为抗剪连接方式的试件的受力性能差于采用栓钉和钢筋桁架与栓钉作为抗剪连接方式的试件.各试件的塑性和延性指标见表3，可知各试件最终破坏时的跨中挠度δu均超过100 mm（L0/27），塑性系数（Mu/My）均超过1.35，挠度延性比（δu/δy）均大于7，说明各试件均具有良好的延性和较高的承载能力.与其它试件相比，试件UXL1-T破坏时的跨中挠度和延性明显更小，说明其抗剪性能不足.

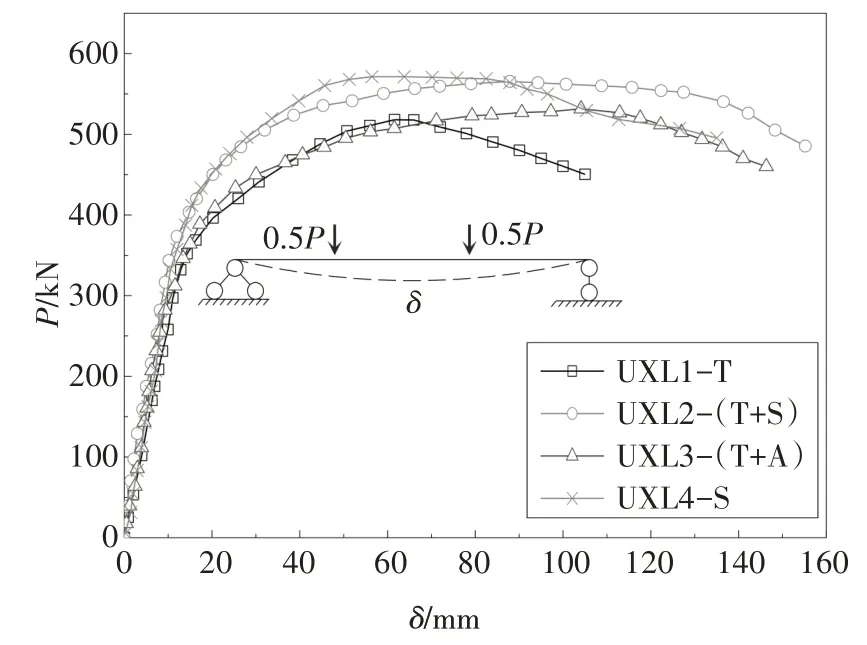
图5 P-δ曲线Fig.5 P-δ curves of specimens

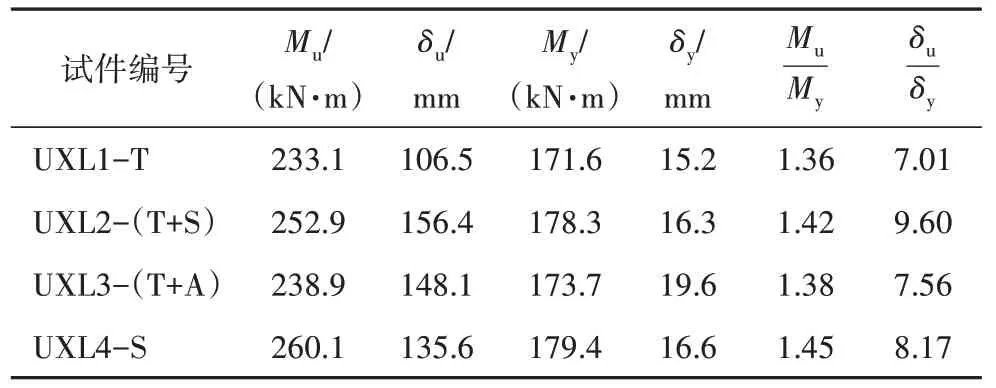
表3 塑性及延性分析Tab.3 Plasticity and ductility analysis

2.3 P-S曲线

各试件端部U 形钢与肋部混凝土的水平相对滑移较小，此处忽略不计.图6 为各试件从开始加载至达到极限荷载Pu时，U 形钢与翼板混凝土的水平相对滑移S随荷载P变化的曲线（P-S曲线），可知试件UXL4-S 在极限荷载时的水平相对滑移值Su仅为0.6 mm，而试件UXL1-T 的Su为8 mm，说明仅将钢筋桁架作为抗剪连接方式的抗剪性能较差.与试件UXL1-T 相比，试件UXL2-（T+S）的Su为0.5 mm，说明在钢筋桁架的基础上布置适量栓钉能提高试件的抗剪连接性能；试件UXL3-（T+A）的Su也为8 mm，说明在钢筋桁架的基础上布置角钢对试件端部水平相对滑移值影响不大，可能是因为角钢抗剪承载力明显大于栓钉，布置的角钢纵向间距过大导致其抗剪连接性能未充分发挥.

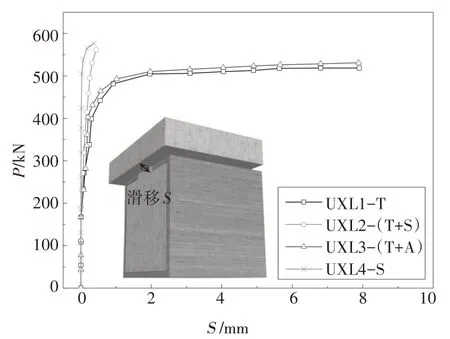
图6 P-S曲线Fig.6 P-S curves of specimens

2.4 P-ε曲线

各试件混凝土的荷载-应变曲线相似，仅以试件UXL4-S 为例（图7），可知翼板混凝土在有效宽度内的压应变近似相同，且破坏时均达到了极限压应变0.003 3.以B5处应变片为例，各试件跨中截面U形钢下翼缘的荷载-应变曲线见图8，可知在0.8Pu时各试件的U形钢下翼缘均已屈服.以试件UXL1-T为例，其跨中截面U 形梁的应变分布见图9，可知试件的中和轴随着荷载增大逐渐上移且始终位于翼板混凝土内，混凝土大多受压，U形钢受拉，材料利用比较充分，且构件在弹性阶段和弹塑性阶段均符合平截面假定.

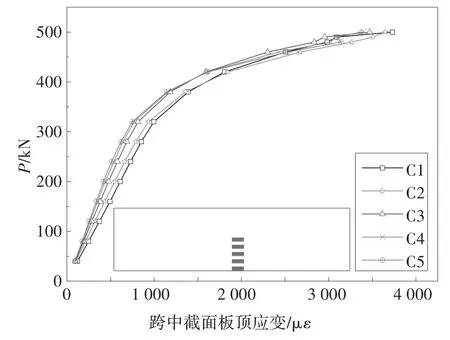
图7 混凝土荷载-应变曲线Fig.7 P-ε curve of concrete

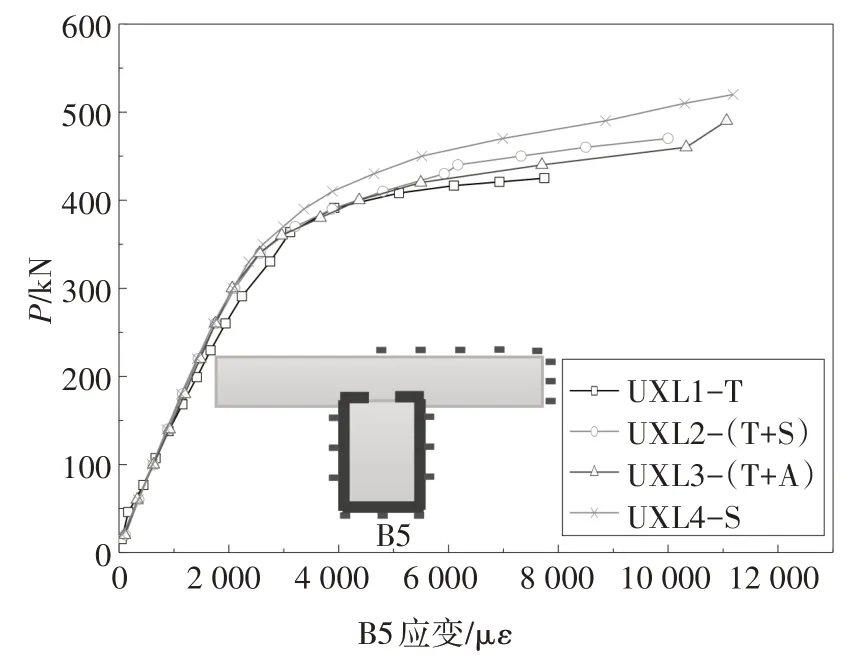
图8 U形钢下翼缘荷载-应变曲线Fig.8 P-ε curve of the lower flange

图9 U形梁应变分布Fig.9 Strain distribution of U-shaped steel-concrete composite beam

3 有限元分析

3.1 模型建立

采用ABAQUS［19］建立有限元模型，模型中钢材均采用线性强化应力-应变关系，混凝土采用《混凝土结构设计规范》（GB 50010—2010）［20］推荐的混凝土本构关系.混凝土、栓钉、角钢等采用C3D8R 实体单元，U 形钢采用S4R 壳单元，钢筋桁架的横向钢筋和受力纵筋采用T3D2 杆单元，钢筋桁架作为抗剪连接件，不能忽视其腹杆钢筋传递剪力的作用，故采用B31梁单元来模拟.抗剪连接件与U形钢上翼缘的焊缝为绑定关系.U 形钢与混凝土采用面与面接触，切向行为定义为摩擦型，摩擦系数取0.4，切应力取0.6 MPa；法向行为定义为硬接触型，即单元间相互挤压时完全接触，单元分离时允许接触面脱开.

3.2 有限元分析结果

3.2.1 应力云图

以试件UXL1-T 为例，有限元分析的应力云图如图10所示，可知U形钢在纯弯区内的拉应力最大，且下翼缘和腹板绝大部分已屈服，同时翼板混凝土塑性应变较大的区域与试验翼板混凝土纵向裂缝出现的位置较吻合（图4（d））.在剪跨区内，钢筋桁架的下弦钢筋应力较大，且发生明显变形，说明钢筋桁架在抵抗界面纵向水平剪力和限制翼板混凝土与U 形钢的相对滑移方面发挥较大作用，可作为新型的抗剪连接件使用.

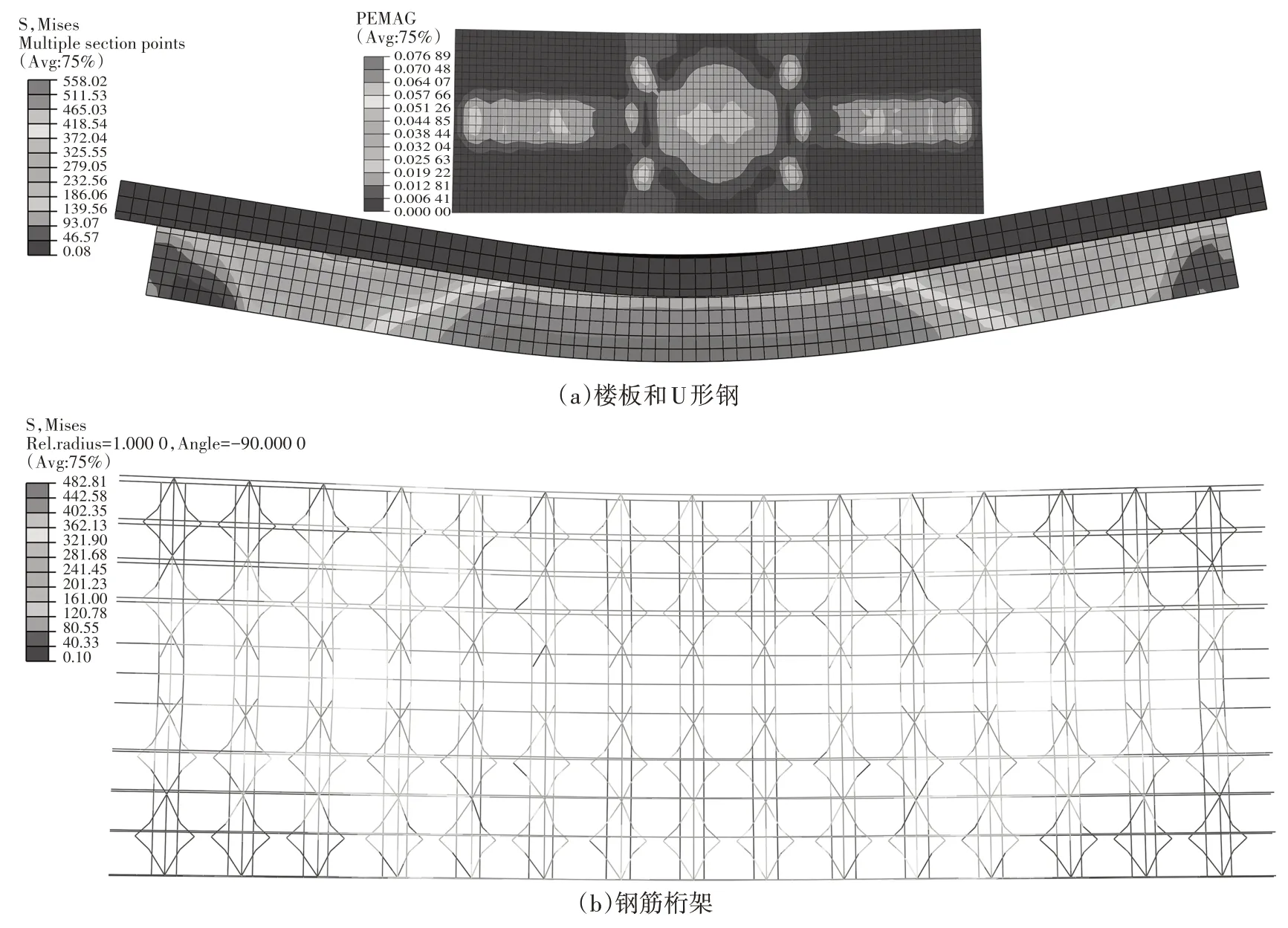
图10 试件UXL1-T的应力和应变云图Fig.10 The stress and strain cloud of specimen UXL1-T

3.2.2P-δ曲线对比

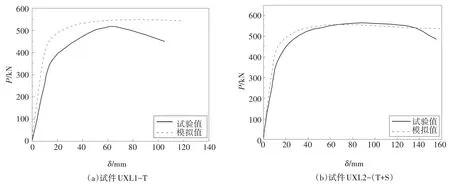
试验和有限元分析P-δ曲线对比见图11，可知试件UXL2-（T+S）和试件UXL4-S 的有限元计算曲线与试验曲线吻合较好，而试件UXL1-T 和试件UXL3-（T+A）则偏差较大，可能是因为试件UXL1-T和试件UXL3-（T+A）无法达到完全抗剪连接，抗剪连接性能不足导致颈部混凝土被剪断而使承载力和刚度降低.同时各试件有限元分析的承载力约为试验承载力的1.03 倍，因为有限元分析没有考虑混凝土实际存在的内部缺陷，也未考虑钢筋与混凝土之间的相对滑移，导致有限元计算的刚度和承载力值偏高，但误差在可接受范围之内，有限元计算和试验的结果对比见表4.

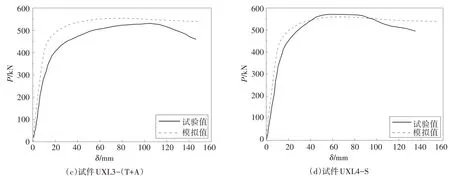
图11 试验和有限元的P-δ曲线对比Fig.11 Comparison of P-δ curves between test and finite element analysis

3.2.3 端部滑移对比

试验和有限元分析的端部滑移值对比见表4，可知对于完全抗剪连接的试件UXL2-（T+A）和试件UXL4-S，有限元分析的滑移值Su1和试验滑移值Su吻合较好；对于抗剪连接性能不足的试件UXL1-T 和试件UXL3-（T+A），由于试件颈部混凝土被剪断，而模型只考虑了混凝土的损伤，未考虑其断裂行为，故试验滑移值取颈部混凝土被剪断对应的值，且有限元滑移值偏小.

表4 有限元和试验结果对比Tab.4 Comparison of experimental results and finite element analysis results

4 U形梁正弯矩受弯承载力

周学军等［21］对翼缘外翻U 形梁在正弯矩作用下的极限受弯承载力进行了推导，并提出了公式应满足的基本假定.本试验采用不同抗剪连接方式的翼缘内翻U 形梁，同时梁底布置了受拉纵筋，根据以上试验研究和有限元分析，提出当采用钢筋桁架作为抗剪连接件、且U 形梁能达到完全抗剪连接时，其在正弯矩作用下的受弯承载力计算公式及应满足的基本假定：

1）U 形钢与肋部混凝土和翼板混凝土能共同工作，截面应变符合平截面假定；

2）极限状态下中和轴以上U 形钢完全受压屈服，中和轴以下U 形钢和钢筋完全受拉屈服，考虑梁底受拉纵筋的抗拉贡献；

3）极限状态下受压区混凝土应力图形用等效矩形应力图形代替，混凝土压应变达到极限压应变，且合力作用点位于等效矩形应力受压区中心；

4）混凝土主要参与受压且抗拉贡献小，故不考虑受拉区混凝土的抗拉作用和翼板混凝土内钢筋的抗压作用.

根据以上假定可得U 形梁在正弯矩作用下的截面应力分布，如图12 所示.对截面任一点取力矩平衡即可得到完全抗剪连接U 形梁在正弯矩作用下的受弯承载力计算公式.

（a）当αfcbehf≥fyAa+fsyAs时，塑性中和轴在翼板混凝土内（图12（a））：

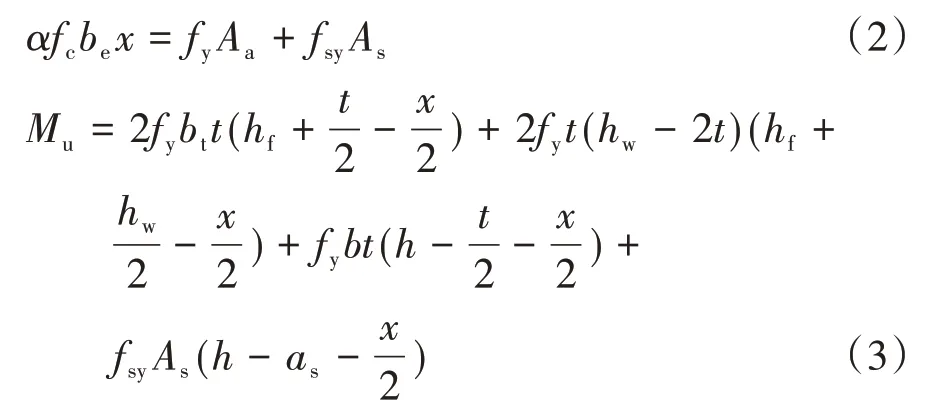
（b）当αfc[behf+t(b-2bt)]+2fytbt≤fy(Aa-2tbt)+fsyAs时，塑性中和轴在U 形钢腹板内（图12（b））：

式中：fsy为梁底纵筋屈服强度；be为翼板混凝土的有效宽度［16］；x和xc分别为混凝土等效和实际受压区高度；α和β分别为混凝土等效矩形应力图形应力值系数和高度系数［20］；As为梁底纵筋的面积；Aa为U 形钢截面面积；Ac为等效受压区混凝土面积；其余参数含义详见图12.

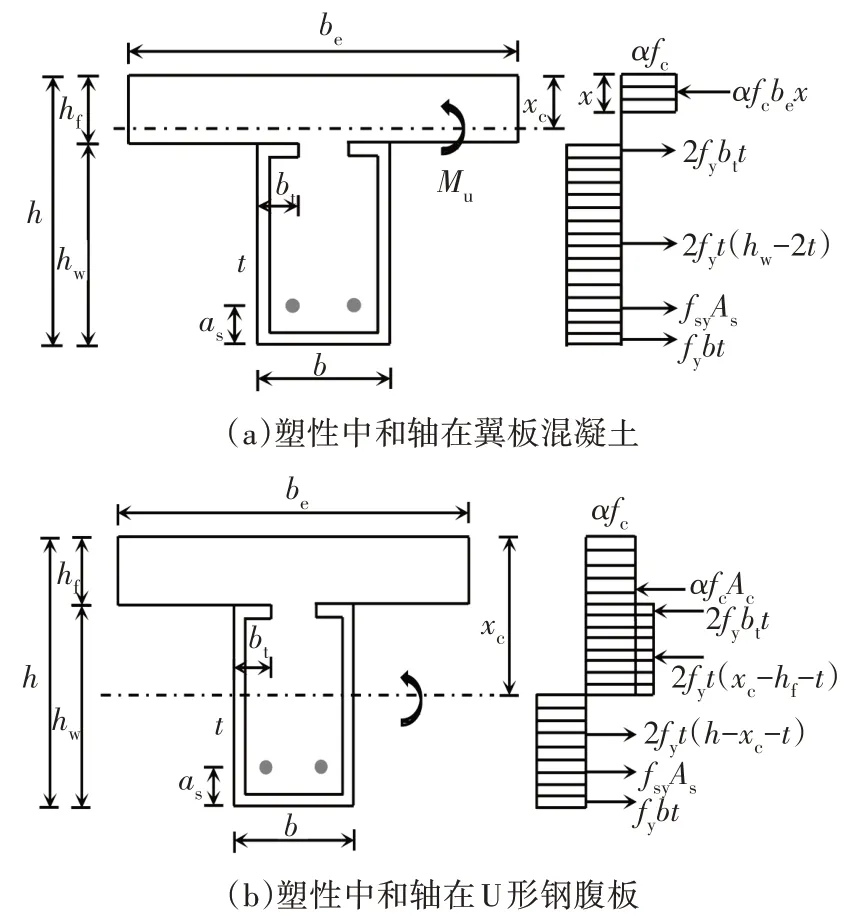
图12 U形梁截面应力分布Fig.12 Stress distribution of U-shaped steel concrete composite beam

根据式（2）～式（3）计算得到完全抗剪连接的试件UXL2-（T+S）和试件UXL4-S 在正弯矩作用下的受弯承载力（表4），可知理论计算值与试验值吻合较好，且具有8%左右的安全储备.

5 结论

通过对4根采用不同抗剪连接方式的U形钢-混凝土组合梁进行静力加载试验研究、有限元分析和受弯承载力理论推导，得出以下结论：

1）试件的破坏分为弯曲破坏和滑移破坏.当抗剪连接件配置合理，试件破坏时端部相对滑移值较小，发生弯曲破坏；当抗剪连接件配置不合理，试件破坏时端部颈部混凝土被剪断，相对滑移值较大，发生滑移破坏.

2）各试件延性系数均大于7，塑性系数均超过1.35，具有良好的延性和较高的承载力.

3）各试件的抗剪连接构造能限制竖向掀起，但当抗剪连接性能不足时，端部滑移明显增大.

4）钢筋桁架作为抗剪连接方式的试件不满足完全抗剪连接时，可再布置适量栓钉以提高其组合作用.采用钢筋桁架和钢筋桁架+角钢作为抗剪连接方式的试件的承载力和刚度明显小于采用栓钉和钢筋桁架+栓钉作为抗剪连接方式的试件.

5）提出了完全抗剪连接的U 形梁在正弯矩作用下的受弯承载力计算公式和基本假定，公式具有8%左右安全储备.