考虑水力工况的风机盘管系统建模方法与辨识

赵 安 军， 张 萌 芝， 于 军 琪*， 杨 航 杰， 董 菲 菲， 周 敏

(1.西安建筑科技大学 建筑设备科学与工程学院，陕西 西安 710055；2.西安建筑科技大学 信息与控制工程学院，陕西 西安 710055；3.中国建筑西北设计研究院有限公司，陕西 西安 710015)

0 引 言

近年公共建筑能耗已经占到中国建筑能耗的42%，而空调系统能耗在公共建筑能耗中的占比高达60%[1].风机盘管系统作为公共建筑中最为常见的空调系统末端设备，其运行效率与空调系统整体能耗紧密相关.

在风机盘管[2]装置的建模研究中，Jagirdar等[3]建立了干燥剂涂覆翅片管热交换器的热和质量交换的数学模型，该模型考虑了固体侧传质阻力以及散热片效率，揭示了盘管几何参数、水的质量流量和空气流速对干燥剂涂覆翅片管的除湿和吸附排热性能以及增强型空调系统在暖湿条件下性能的影响.Bai等[4]在对盘管换热器复杂物理模型合理简化的基础上，建立了相应的动态换热数学模型，并求出了盘管换热器换热量与其各进口参数间的动态关系式.迟光亮等[5]利用分段集总参数法建立了肋片管表冷器在湿工况下的动态数学模型，得到了肋片管表冷器各微元段水侧温度和空气侧温湿度随时间的变化关系，以及流体入口温度和流速扰量对表冷器换热量的影响.Martinevi等[6]、Castilla等[7]、Maddah等[8]建立了非物理模型，通常以围绕工作点的简单线性形式或采用神经网络训练模型，当在训练范围之外操作时，精确度降低.Ranade等[9]结合风机盘管传热过程质量和能量平衡，在机理建模的基础上通过非线性在线识别方法估计最多6个模型参数，建立了动态风机盘管数学模型.Lin等[10]以空气和水/乙二醇防冻混合物为传热流体，使用神经网络模型来模拟紧凑翅片管风机盘管的换热性能，结果表明经过适当训练的神经网络可以模拟紧凑型风机盘管的整体和局部特征.Bacher等[11]、D′Antoni等[12]通过电加热获取建筑区域的热能数据，但由于大多数商业与住宅建筑都有水或空气基加热/冷却循环，实验效果并不理想.Sunu等[13]建议使用压降传感器来确定通过风机盘管的流量，然而由于需要大量昂贵的传感器和相应的安装成本，当应用于建筑中每一个风机盘管时，会造成成本上升和工期延长.

以上研究中所采用的控制模型大都只针对风机盘管的热力学性能，并未将水力学性能与热力学性能结合考虑，并且模型建立主要反映风机盘管的物理过程，并未专门针对控制进行建模，不易于在工程控制中进行应用.且上述研究中大多使用白箱与黑箱建模，模型精确度较低，获取数据困难，在实际工程中难以操作.而灰箱建模可在较宽操作范围内精确地捕获风机盘管非线性特性，通过实验数据辨识制造商未能提供的相关参数，在广泛的操作条件下给出与实际性能的准确匹配，在实际工程中简单易行.为此，本文提出面向控制的风机盘管系统建模方法，将风机盘管系统所涉及的水力学和热力学模型进行整合，形成风机盘管热工水力模型，用以支撑根据建筑每个区域的热需求实现动态流量计算和风机转速控制.

1 风机盘管系统模型

多个风机盘管机组并联到一条供回水管道形成风机盘管系统，所用冷媒水或热媒水由制冷机房或热交换站集中供应，如图1所示.风机盘管系统本质上是冷热媒体流动和介质间热交换的复杂物理过程，通过分析影响风机盘管系统运行工况相关物理机理特征量、传热流体流动和介质间热交换的关系，建立物理机理模型，能够定量计算和预测风机盘管系统的物理表现和特性.为得到更精确的区域控制能力，面向控制的风机盘管系统模型由水力学系统和热力学系统组成.

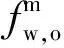
1.1 水力学模型

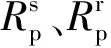
考虑水通过管道的压力损失Δpp，包括静水压力损失Δph和摩擦压力损失Δpf.描述管道中总压力损失的方程为

Δpp=Δph+Δpf

(1)

静水压力损失与管段入口和出口之间的高度差Δh有关，即

Δph=ρgΔh

(2)

其中ρ是密度，g是重力加速度.摩擦压力损失与管道内径d和长度L有关，即

(3)

其中μ是水的动态黏度.假设这里的L考虑过管道微小损失，是使用等效长度法后得到的值[14].

对于电路的每个回路，知道水力阻力和质量流量，可以通过基尔霍夫定律表示风机盘管的压降.

(4)

式中：Δpj是平行分支的总压降，包括通过风机盘管的压降及相关垂直供应和返回管道的压降；Δpk+1=Δpo是整个系统的整体压降；fw，i是水的质量流量.基于遗传算法[15]通过求解以下优化问题可得出风机盘管的最优流量：

(5)

1.2 热力学模型

由水力学模型得到了各风机盘管流量分布.水流经过各房间风机盘管，对各个区域温度进一步调控.考虑风机盘管内部热传递中加热/冷却水的对流、通过热交换器的热传导以及待加热或冷却空气的对流，对于建模做出以下假设：

(1)风机盘管有4种可能的风机速度：关闭，低、中和高速，分别表示为O、L、M、H.

(2)空气质量流量fa在风机盘管内随风机速度而变化，并假定风机的每种速度是恒定的.

(4)假设回风温度等于室内温度.

传热系数Uo是非线性函数，且风机速度影响着水流量，如下式所示：

(6)

当风机速度s一定，空气质量流量fa不随时间显著偏离.因此，估计所有风机速度的独立功能是合理的，从而避免了求解难以测量的气流信息.通过将气流信息与风机速度相关联，则

(7)

其中a、b、β是基于物理系统属性或通过识别确定的参数，且β与风机速度无关，视为盘管的公共参数.

当风机处于关闭状态时，风机盘管为恒定传热系数的普通散热器单元，因此b=0.在供暖季节，进入管道的空气温度被认为等于区域温度，而在供冷季节，落地式机组的热力性能下降，冷却后的空气倾向于停留在地板上而不与区域空气混合，因此进入的空气温度低于区域温度.通过引入每种风机速度的修正系数ε，可以改进所述的季节性效应：

(8)

把风机盘管空气区域的热效应过程看作一个稳定过程，风机盘管的传热系数进一步影响着室内的温度与热能，风机盘管的最终热力学模型采用切换线性模型的形式：

(9)

(10)

最小二乘法是一种在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域得到广泛应用的数学工具[16]，采用基于最小二乘法的模型辨识会得到比较好的辨识结果：

基于传热系数特性参数的辨识，得到区域热功率.

模型计算具体步骤描述如下：

Step1初始化，从制造商目录中选取管道尺寸L、压降p、阻力R等数值，作为初始值.

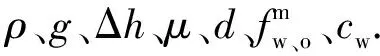
Step3根据建立的模型，由式(5)基于遗传算法求解流量分配，得到各盘管流量fw，i.

Step4若盘管两端的压降Δpj改变，则重复流量求解的操作，流量分配值fw，i即为输出变量.

Step5对选择进行实验的房间盘管进行数据分析，建立基于风机速度s的切换线性热力学模型.

Step6基于最小二乘法辨识得出参数a、b、β、ε，为传热系数Uo的特性参数.

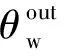
2 模型验证

选取西安建科大厦进行验证，该区域面积1 500 m2，高3 m，外围护两面是混凝土墙，厚度为35 mm，顶部是混凝土板，厚度为30 mm.以其中一层为例，走廊两边为办公室区域，共14间独立办公室，每个房间设定为一个空间单元，由中央空调系统统一供冷.其中，每个空间单元分别设置1个风机盘管；此外，在每个楼层房间的风机盘管供水管道上安装热量计(UH50-A50-00)，采样时间间隔为1 min，测量供水和回水温度、温差、水流量、热功率.管道长度定义为两个连续风机盘管之间水平段长度或风机盘管与热量计之间的长度(风机盘管采用格力品牌产品).流量测量采用超声波流量计通过检测流体流动对超声束(或超声脉冲)的影响，从而得到流量.测量过程采用基于时差法的DTS-100H手持式超声波流量计，即介质在管道中的流速与超声波沿介质顺流的传播时间线性相关[17].垂直供水和回水管道(包括管件)的等效长度对于所有单位和数量均相同，由于管道具有良好的保温性能，在以下计算中忽略了输送热损失.

如图3所示，根据制造商目录参数得出风机盘管的压降特性，fw表示通过风机盘管的水质量流量，Δp表示通过风机盘管的压降.

表1为风机盘管单元(fan coil unit，FCU)水力学系统各支管相关参数.当环境所需负荷发生改变时，供水流量相应改变.表2是在各楼层供水流量分别为0.36、0.58、0.67 kg/s工况下，各盘管流量分配情况.

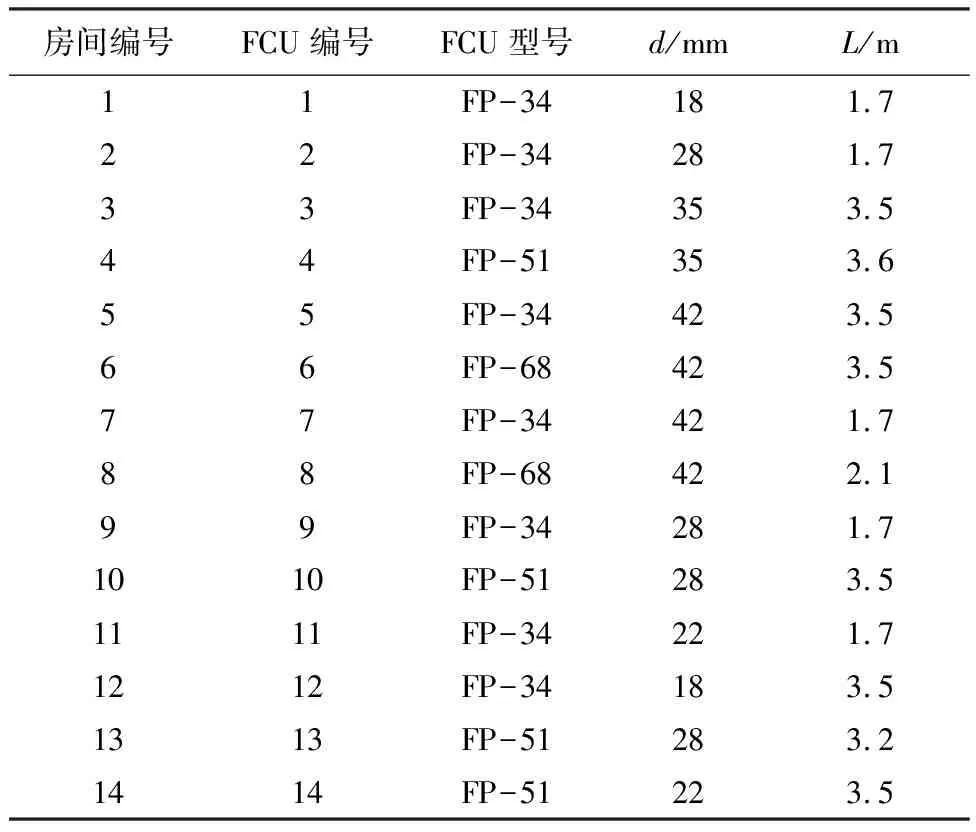
表1 FCU水力学系统各支管相关参数

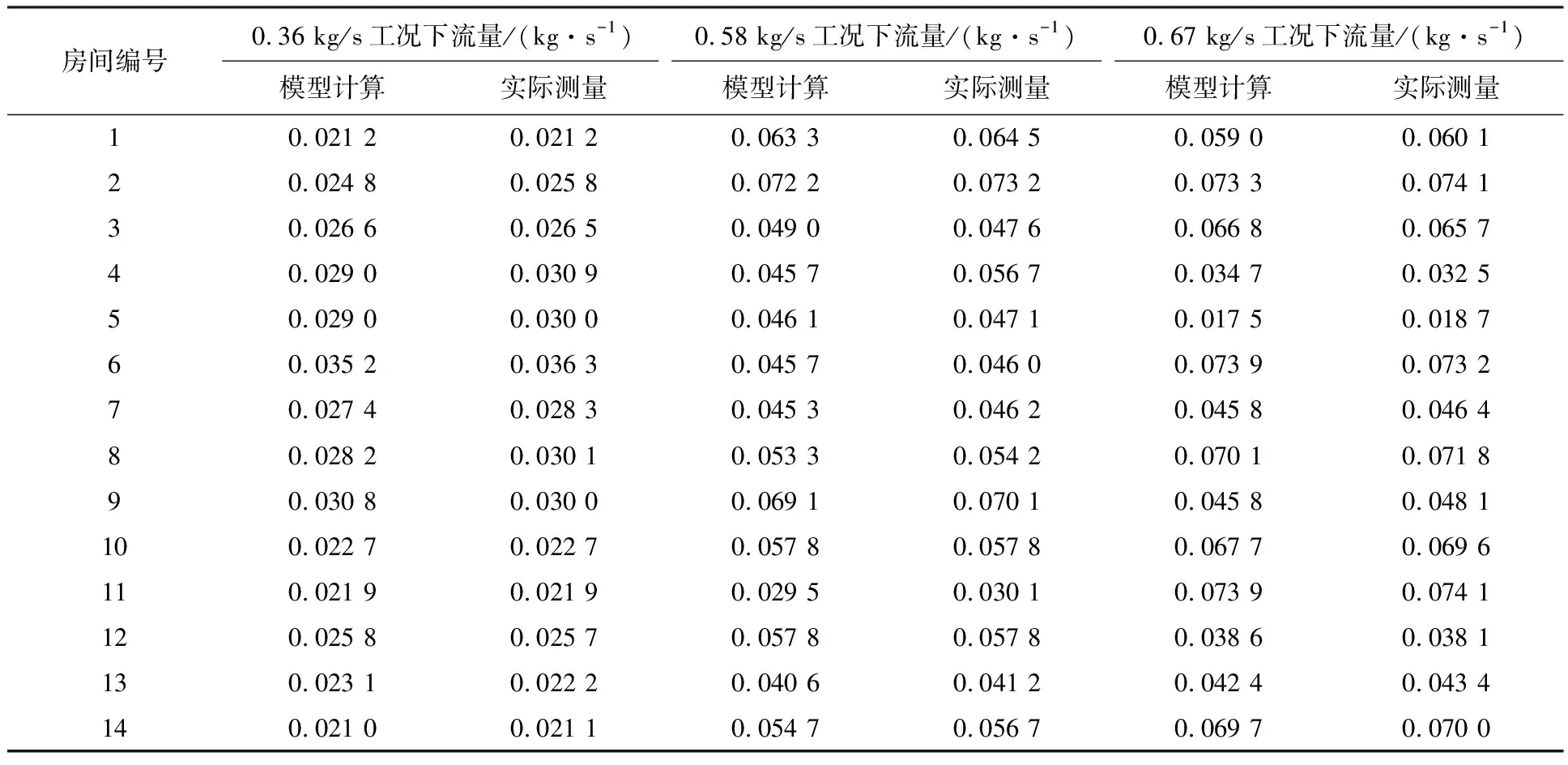
表2 不同工况下流量分布

在3种不同工况下，即系统总供水流量分别为0.36、0.58、0.67 kg/s，RMSE分别为0.000 95、0.003、0.001；MAPE分别为0.024、0.032、0.024，误差不超过6%，满足实验要求.从误差分析指标可以得出水力学模型所求的流量分配值与实际测量值基本吻合，验证了所建立模型的准确性.

表3显示了基于制造商目录参数，通过建立的热力学模型计算辨识出的FP-34参数a、b、ε、β，在不同风机速度下都给出了修正系数的取值；ε在供冷季和供热季取值并不一致，且在供热季时修正系数不随风机速度的变化而改变.

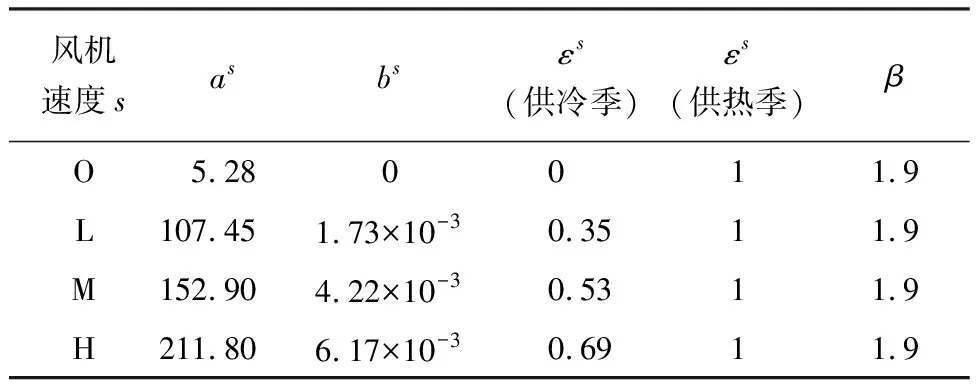
表3 Uo(s，fw)的功能参数表

选取第10个房间对模型展开验证，夏季供冷时间一般在6～9月，6～7月时系统处于低工况运行状态；8～9月室外温度较高，系统处于高工况运行状态，取实验中一天内8：00～22：00时间段进行测量，采样时间间隔为1 h，办公时间为9：00～18：00，有时会出现加班情况，延长至20：00，所测得的回水温度以及区域功率和模型所得结果一致，证明了模型的真实性与实用性.夏季高、低工况下供回水温度、室内区域温度以及热功率消耗分别如图4、5所示.

夏季室内舒适区的温度一般设定在23～27 ℃.如图4(a)所示，综合考虑水力学与热力学性能后的回水温度基本在舒适范围内波动，测量与模拟回水温度变化一致，且稳定性较高.由图4(b)可以看出，室外环境温度较高时，室内的冷负荷需求随之增多，风机开度变大，进一步调节改善室内温度，新的末端盘管控制模型可以使室内温度在舒适范围内波动.高工况下，9：00时风机开度已经处于中高速状态来调节室温；13：00～14：00 中午休息时间，风机开度降低，室内温度有所升高.由图4(c)可知，风机开度越大，消耗的功率越多，办公时间内运行能耗与风机开度的走势保持一致，实验得出的区域功率与热量计测量值走势也基本一致，这说明末端盘管模型控制对获得精确的区域功率效果显著.其中，供回水温度的MAE和RMSE分别为0.101和0.17；运行能耗的MAE和RMSE分别为0.014和0.008 5.

夏季低工况下的供回水温度如图5(a)所示，受实际运行工况下室外环境温度影响，低工况运行下的温差范围明显变小且模型计算的回水温度与实际测量值基本保持一致，虽有较小的偏差但都在误差允许范围内.如图5(b)、(c)所示，低工况下，室外温度变化幅度很小，仅消耗较小的功率就可达到室内温度舒适范围，且夜间休息时，室内设定温度比白天略高，所以夜间功率消耗低.其中，供回水温度的MAE和RMSE分别为0.108和0.08；运行能耗的MAE和RMSE分别为0.027 和0.014.

供热状态的时间从11月中旬维持到第二年3月中旬，室外温度过低时，系统处于高工况运行状态，要满足高负荷的运作需求；温度稍有回升时，低工况的状态便能满足室内舒适性.冬季高、低工况下供回水温度、室内区域温度以及热功率消耗分别如图6、7所示.

如图6(a)所示，在冬季高工况下，受室外环境中冷空气影响，供热温度产生一定的波动，可通过增加保护管道措施来改善；模拟回水温度与测量值均在舒适范围内且保持变化趋势一致.如图6(b)所示，冬季时中午温度较早晚高些，改变风机开度，温度也随之改变；早上温度低，调大风机开度以保证室内热舒适，中午可随室温与需求适当降低开度，在保证人体温暖舒适的前提下适当节能.能耗结果如图6(c)所示，冬季早晚温度较低，需要消耗更多功率维持室内温度，模拟能耗有出现偏差情况，这是因为冬季工况下空气温度有时会低于最低限度10 ℃，所以需要耗费更多功率来达到设定温度.其中，供回水温度的MAE和RMSE分别为0.005和0.001；运行能耗的MAE和RMSE分别为0.036和0.017.

如图7(a)所示，相比高工况运行状态，低工况时供回水温差变小，减小运行能耗的同时维持室内舒适性，风机开度变大时回水温度降低，释放更多热量调节室温以满足负荷需求.如图7(b)所示，低工况下热负荷需求较低，高开度的风机运行时间少于高工况状态，且随着风机开度的加大，室内温度升高，舒适性得以满足.如图7(c)所示，低工况运行时，运行能耗低于高工况下的能耗，符合实际情况，在环境温度较低时，为保证工作人员的舒适性，风机处于高开度运行状态，运行能耗增高，温度升高，保证了室内热舒适.其中，供回水温度的MAE和RMSE分别为0.05和0.019；运行能耗的MAE和RMSE分别为0.018和0.009.

3 结 论

(1)基于基尔霍夫定律，构建水力学系统的等效电气模型，用于计算风机盘管系统中各个盘管的流量，实验结果表明模型可以精确反映风机盘管中水流特性.

(2)基于风机盘管的传热系数，热力学模型通过风机开度直接控制每个区域的热能输入，获得建筑物热力学模型识别所需的区域热功率，准确反映风机盘管的传热过程.

(3)采用热工水力模型能更精确反映风机盘管系统的物理特性，从而为室内环境品质控制提供保障与支持，引入被控变量能更好地将模型应用到风机盘管的控制当中，以保持区域的舒适性.所建立的模型可直接用于建筑能源管理系统(BEMS)，用于识别建筑区域热功率，且水力学和热力学模型误差都大大低于6%.