构建沥青基材料力学行为主曲线的两阶段方法

唐 成, 王端宜, *, 胡 聪, 贠 迪, 邓凯聆

（1.华南理工大学 土木与交通学院, 广东广州 510641；2.长安大学 公路学院, 陕西 西安 710064）

沥青和以沥青作为胶结料的沥青砂浆、沥青混合料等沥青基材料的力学行为具有典型的黏弹特性, 且时温特性对其力学行为有重要影响.为研究沥青基材料在宽时间域、宽频率域内的力学行为, 对此类具有热流变简单性行为的材料而言, 通常可采用时温等效原理, 将不同测试温度下窄时间域与窄频率域的数据进行平移, 所得到的光滑曲线称之为主曲线[1］.中华人民共和国航空航天工业部航天工业标准QJ2487-93《复合固体推进剂单向拉伸应力松弛模量及其主曲线测定方法》中, 对固体推进剂松弛模量主曲线的测定进行了规范化, 但尚未出现规范化的沥青基材料主曲线绘制方法.Yin等[2］对沥青与沥青混合料主曲线绘制方法的规范化进行了初步研究.美 国AASHTO R62-13《Standard practice for developing dynamic modulus master curves for asphalt mixtures》（后文称规范方法）对沥青混合料动态模量主曲线的绘制进行了规范化：首先, 将移位因子方程以及缩减频率与频率的关系式代入主曲线模型；然后, 使用规范求解工具或自定义函数拟合的方法进行函数拟合.绘制沥青的动态模量主曲线时, 研究人员也通常采用规范方法[3-4］, 但是该方法的拟合效果受主曲线模型、移位因子方程的选择及拟合初值的选取影响较大.此外, 已有研究成果表明, 沥青混合料层间剪切强度及沥青混合料的力学损伤行为也具有时温等效特性[5-6］.针对此类主曲线模型未知的力学行为, 无法使用规范方法绘制主曲线, 通常采用人工平移的方法, 但是主观因素会严重影响平移的准确度.

基于此, 本文根据主曲线的定义, 提出将主曲线的获取与拟合进行分离的两阶段方法（TSM）, 以期为沥青基材料流变学的研究提供借鉴.

1 试验

1.1 原材料

基质沥青（BA）为壳牌70#沥青, 用SBS改性沥青（SBSMA）成型沥青砂浆试件, 沥青的基本性能指标见表1；集料为辉绿岩, 油石比（质量比）为0.12.试件成型方法参考文献[7］, 试件的高度为40.0 mm, 直径为12.5 mm, 孔隙率（体积分数）为1.01%.沥青砂浆的级配见表2.

表1 沥青的基本性能指标Table 1 Basic property indicators of asphalts

表2 沥青砂浆的级配Table 2 Gradation of asphalt mortar

1.2 试验方法

采用马尔文Kinexus型动态剪切流变仪对沥青与沥青砂浆进行不同测试温度T下的频率扫描试验.基质沥青的测试温度Ta=4、16、28、40、52、64、76℃；沥青砂浆的测试温度Tm=5、15、25、35、45、55℃.测试频率f为0.1～30.0 Hz, 并按对数等间距取16个测试点.橡胶的测试温度Tr=-60～100℃（间隔10℃）, 其频率扫描结果参考文献[8］.基质沥青试验数据用于对比采用两阶段方法与规范方法绘制主曲线时的拟合效果；沥青砂浆及橡胶试验数据用于检验采用两阶段方法绘制主曲线的稳健性.

2 主曲线的获取

2.1 测试温度为参考温度时移位因子的计算

满足时温等效原理的力学行为均可使用主曲线进行描述, 如沥青基材料的动态模量G*、松弛模量及蠕变柔量等.为便于阐述具体计算过程, 本文以构建动态模量主曲线为例, 论述具体的计算细节.计算可分为以下5个步骤.

第1步：选择某一测试温度作为参考温度TRef.

第2步：确定相邻测试温度插值区间.提取相邻测试温度T1、T（2T1＜T2）的动态模量测试结果, 由T1下最小测试频率的动态模量G*1与T2下最大测试频率的动态模量G*2, 可确定区间[G*1,G*2］为插值区间.

第3步：计算相邻测试结果水平移动范围.在区间[G*1,G*2］内按对数等间距选择n个插值点, 通过插值 确 定T1下动 态 模 量为G*1、G*2时 的 频 率分 别 为fT1,n、fT1, 1,T2下 动态模 量为G*1、G*2时的 频率分 别为fT2,n、fT2, 1；令Δf1=fT2,n-fT1,n, Δf2=fT2, 1-fT1, 1, 当 固 定T1下 的 数 据时,T2下的数据水平移动范围为[-max（Δf1, Δf2）, -min（Δf1, Δf2）］.

第4步：用寻优算法确定相邻温度的移位值.将第2步确定的水平移动范围按对数等间距划分为m份, 本文n、m分别取25、100, 接着将T2下的动态模量数据按划分后的水平移动范围进行水平移动, 并计算平移后两曲线在区间[G*1,G*2］的n个插值点角频率ω差值的范数Norm, 寻找使Norm最小的水平移动值j*.j*即为固定T1下的数据时,T2下数据的水平移位值.计算过程可表示为：

第5步：计算移位因子.重复第2～4步, 求取所有相邻温度的移位值, 并将测试温度与参考温度之间求取的所有移位值求和, 同时根据测试温度与参考温度的高低, 确定数值的符号, 当测试温度低于参考温度时取正号, 高于测试温度时取负号.

计算示意图见图1（图中T3、T4、T5、T6、T7均为测试温度）.需要说明的是, 上述算法针对的是相邻测试温度的测试数据在y轴有重叠区域, 当数据没有重叠区域时, 可使用线性方程或多项式分别对测试数据进行拟合, 然后进行外延来获取重叠区域, 再使用上述算法进行计算即可.

图1 计算示意图Fig.1 Calculation diagram

2.2 目标温度作为参考温度下移位因子的求取

以不同的测试温度Ta作为参考温度, 使用上述算法得到基质沥青的移位因子αT, 结果见图2.由图2可见, 以不同测试温度作为参考温度时, 在半对数坐标下, 所有移位因子曲线形态完全相同, 均仅在y轴发生了相对移动.这是因为绘制主曲线时, 选择不同测试温度作为参考温度时, 相同测试结果在半对数坐标轴下, 其绝对距离会发生变化, 但是相邻测试温度的测试结果在对数坐标下, 相对移动的距离并未发生变化.求取任意参考温度下的移位因子, 只需将移位因子在半对数坐标下沿着y轴进行垂直移动即可, 但是需保证在选取的参考温度下移位因子的对数值为零.基于此, 本文通过移位因子曲线插值并竖向移动的方法来确定任意目标参考温度下的移位因子, 具体过程为：在得到以测试温度作为参考温度时的移位因子曲线后, 使用插值法确定目标参考温度下的移位因子, 再将所有测试温度下的移位因子减去目标参考温度的移位因子, 即可得到最终的移位因子曲线.求取参考温度为4℃时的移位因子曲线后, 通过插值并竖向移动来确定参考温度为25℃时的移位因子曲线的过程示意图见图3.

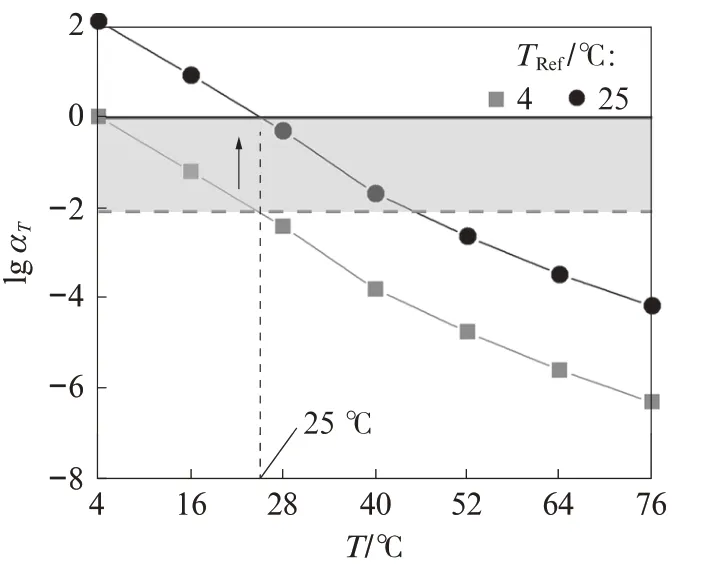
图3 移位因子竖向移动示意图Fig.3 Schematic diagram of vertical movement of αT

2.3 测试结果平移获取主曲线

在得到目标温度下的移位因子后, 可在对数坐标下进行测试结果平移, 从而获取主曲线.基质沥青选用Ta=15、25、35℃作为参考温度, 其动态模量G*主曲线及使用相同移位因子的相位角δ主曲线见图4.由图4可见：对数坐标下不同参考温度的动态模量主曲线完全相同且光滑, 而采用规范方法绘制主曲线时由于参考温度的不同, 平移后的主曲线经常会出现突变, 并导致主曲线不顺滑, 这表明本文所提出的方法具有很高的精度与稳健性；相位角测试结果使用与绘制动态模量主曲线相同的移位因子时, 也能得到相对光滑的相位角主曲线, 这表明试验所用的沥青具有热流变简单性.此外, 相较于规范主曲线计算方法, 本文提出的两阶段方法在绘制主曲线过程中, 不需要预设主曲线模型与移位因子方程, 可根据需要在获取主曲线后, 使用主曲线模型或移位因子方程对主曲线或移位因子进行拟合, 并最终确定模型参数.

图4 基质沥青的动态模量与相位角主曲线Fig.4 Master curves of G*and δ of BA

3 拟合效果对比

选取25℃作为参考温度, 采用两阶段方法、规范方法分别结合Christensen-Anderson（CA）模型（见式（1））、Christensen-Anderson-Marasteanu（CAM）模 型[9］（见式（2））对基质沥青的主曲线进行拟合, 规范方法采用WLF方程作为移位因子方程（见式（3））.

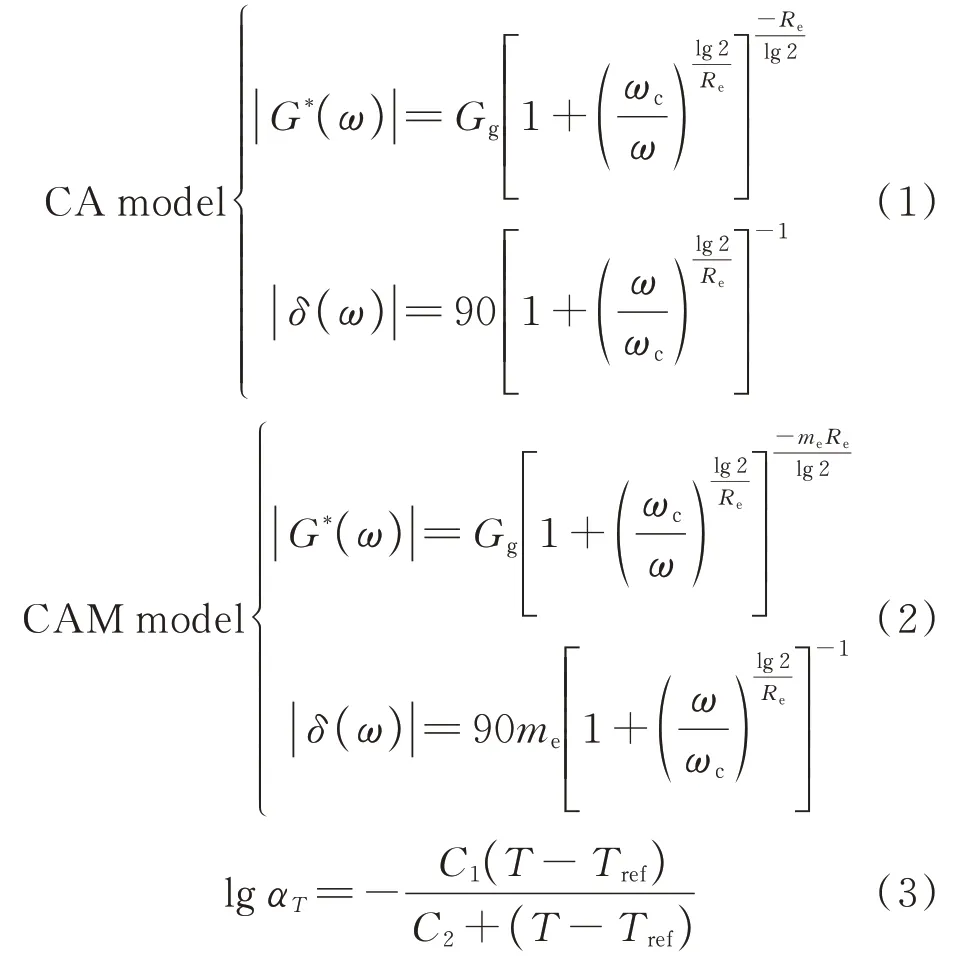
式中：Gg为玻璃态模量, 模型拟合时取109Pa；ωc为交叉频率；Re为流变学指数；me为形状参数；C1、C2为材料常数.

基质沥青主曲线采用两阶段方法与规范方法的拟合结果见图5.由图5（a）、（b）可见：两阶段法结合CA模型（TSM+CA模型）及两阶段法结合CAM模型（TSM+CAM模型）对基质沥青的动态模量主曲线均具有较好的拟合效果, 平滑的动态模量主曲线散点基本分布在拟合曲线上；对相位角主曲线而言, 当角频率ω＞0.1 rad/s时, TSM+CA模型具有较好的拟合效果, 当ω＜0.1 rad/s时, TSM+CA模型拟合曲线会低估真实的相位角值, 而TSM+CAM模型能极大地改善TSM+CA模型的相位角拟合效果.由图5（c）、（d）可见：以WLF方程作为移位因子方程的规范方法并结合CA模型（WLF+CA模型）及CAM模型（WLF+CAM模型）拟合时, 拟合曲线的拟合优度R2均大于0.95, 但是平移得到的主曲线散点数据存在突变且不平滑, 拟合曲线与主曲线散点并不能较好地贴合；采用WLF+CAM模型在一定程度上改善了WLF+CA模型的拟合效果, 特别是相位角主曲线的拟合效果.这是因为CAM模型本身相较于CA模型, 对沥青相位角主曲线的低频段具有更好的拟合效果, 但其拟合效果仍劣于采用TSM+CAM模型, 这主要是因为规范方法采用将移位因子方程及缩减频率与频率的关系式代入主曲线模型进行拟合, 主曲线的确定与拟合同时进行, 取得理想拟合效果的前提是主曲线模型和移位因子方程均具有足够的准确度.

通过比较采用规范方法与两阶段方法绘制主曲线时的拟合效果, 发现主曲线模型和移位因子方程仍有较大的改善空间.已有研究结果表明, 式（4）所示的二次多项式相较于WLF方程具有更好的拟合效果[10］, 但是该方程不满足当T取参考温度TRef时, 移位因子数值为零的要求.为此, 本文提出式（5）所示的改进型二次多项式移位因子方程（ponynomial）.

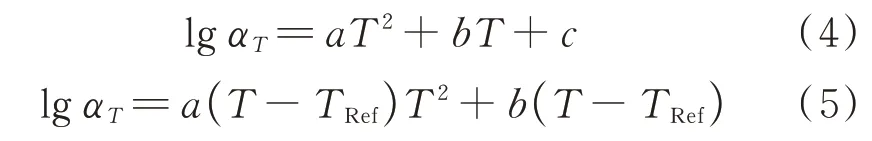
式中：a、b、c均为模型参数.

使用改进型二次多项式移位因子方程并结合CAM模型（ponynomial+CAM模型）对基质沥青的主曲线进行拟合, 拟合效果见图6.由图6可见, 基质沥青动态模量与相位角主曲线采用ponynomial+CAM模型的拟合效果均优于WLF+CAM模型的拟合效果, 这主要是因为改进型二次多项式相较于WLF方程对移位因子具有更好的拟合效果, 说明采用规范方法拟合沥青基材料主曲线时, 默认使用WLF方程会潜在影响沥青基材料主曲线的拟合效果.比较图6与图5（b）可知, 采用ponynomial+CAM模型的拟合效果与TSM+CAM模型仍存在较大差距, 这是因为ponynomial+CAM模型虽然改善了CA模型与WLF方程的准确度, 但是仍然不能完美地刻画沥青的主曲线与移位因子, 这也是研究人员提出更多新型主曲线拟合模型与移位因子方程的原因.

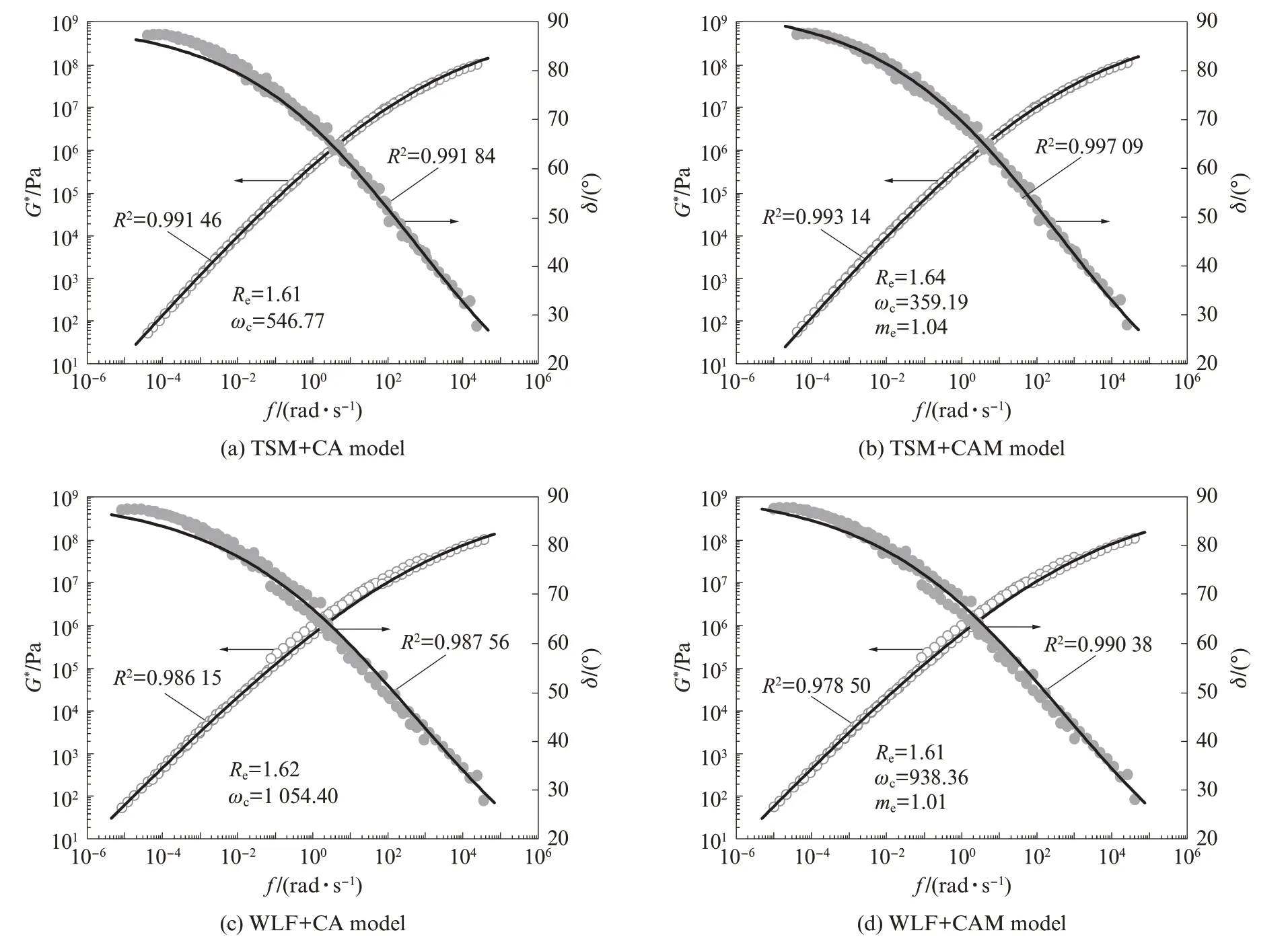
图5 基质沥青主曲线采用两阶段方法与规范方法的拟合结果Fig.5 Fitting results of two-stage method and traditional method for master curves of BA

图6 基质沥青主曲线采用改进的二次多项式移位因子方程的CAM模型拟合结果Fig.6 Fitting results of ponynomial+CAM model for master curves of BA

由前文比较可知, 采用TSM+CAM模型具有最好的拟合效果, 以此为基准可比较其他方法在主曲线拟合后与真实主曲线数据的偏离程度.基质沥青采用两阶段方法及规范方法拟合后的主曲线见图7.由图7可知：采用TSM+CA模型、TSM+CAM模型拟合的动态模量主曲线具有较好的重合度, 在高频段相位角下主曲线也具有较好的重合度, 但是在低频段会表现出CA模型低估相位角值；比较规范方法拟合主曲线与基准线的位置可知, 使用规范方法拟合的动态模量主曲线会低估动态模量值, 规范方法采用WLF+CA模型、WLF+CAM模型会低估低频段的相位角值而高估高频段的相位角值, polynomial+CAM模型会高估相位角值.动态模量试验是获取沥青基材料松弛模量Prony级数的重要方法[11-12］, 对真实动态模量与相位角数据的低估或高估会影响Prony级数的拟合效果, 并潜在地影响仿真计算结果的准确性.

图7 基质沥青采用两阶段方法与规范方法拟合的主曲线Fig.7 Master curves fitted by two-stage method and standard method of BA

规范方法采用将移位因子方程及缩减频率与频率的关系式代入主曲线模型进行拟合, 移位因子方程的参数与主曲线方程的参数同时确定, 最终的拟合效果与主曲线模型及移位因子方程的准确度存在较大关联.两阶段方法可实现主曲线的获取与拟合过程的分离, 其本质是将移位因子的计算和主曲线的拟合进行了分离.与规范方法相比, 两阶段方法对于参考温度的选择不会影响主曲线的最终形态, 而且可在主曲线的拟合过程中对不同数学模型的拟合精度及适用性进行检验, 对开展主曲线拟合模型与移位因子方程的研究具有重要意义.

4 稳健性验证

为验证两阶段方法绘制主曲线的稳健性, 本研究对沥青砂浆及非沥青基材料橡胶进行主曲线绘制.需要指出的是对于沥青砂浆而言, 当用规范方法绘制主曲线时, 可采用已知主曲线模型进行拟合, 但对橡胶而言并不存在广泛使用的主曲线模型, 因此无法使用规范方法进行主曲线拟合.选取25℃作为参考温度, 采用两阶段方法计算得到沥青砂浆及橡胶的主曲线, 结果见图8.由图8可见, 使用两阶段方法能绘制光滑的沥青砂浆、橡胶的动态模量主曲线, 且能准确地刻画沥青砂浆及橡胶材料相位角主曲线的“单峰”特性, 说明本文所提出的两阶段方法对沥青砂浆、非沥青基材料（如橡胶）的主曲线也有很好的计算效果.

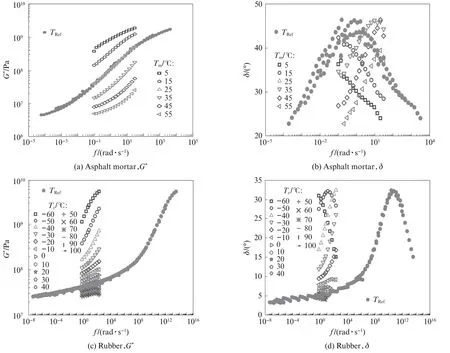
图8 采用两阶段法计算得到的沥青砂浆与橡胶主曲线Fig.8 Master curves of asphalt mortar and rubber by two-stage method

本文仅仅展示了不同材料动态模量与相位角主曲线的计算效果.需要指出的是, 沥青基材料蠕变柔量主曲线或松弛模量主曲线的计算也可使用上述两阶段方法的计算原理进行.此外, 已有的研究成果表明, 沥青混合料层间剪切强度及沥青混合料的力学损伤行为也可使用主曲线描述[7-8］, 两阶段方法对此类问题也有较好的适用性.

5 结论

（1）提出了构建沥青基材料主曲线的两阶段方法, 可实现主曲线的获取与拟合2个阶段的分离.通过移位因子曲线的插值与平移, 可得到任意参考温度下的移位因子与主曲线.

（2）采用两阶段方法绘制主曲线可克服规范方法需要预设主曲线模型与移位因子方程的缺陷, 对力学行为模型未知的材料具有较好的适用性.

（3）使用规范方法结合CA模型或CAM模型拟合主曲线时, 会低估沥青的动态模量, 高估沥青高频段的相位角.两阶段方法在主曲线拟合阶段可对主曲线模型的准确性进行检验, 并可用于主曲线模型或移位因子方程的优化.

（4）两阶段方法不仅对构建沥青基材料黏弹性力学行为主曲线有很好的效果, 对非沥青基材料及具备时温等效特性材料的力学行为主曲线的绘制也具有较好的扩展性.