PE/PVA纤维海砂ECC的拉伸性能与本构模型

姚淇 耀, 陆宸宇, 罗月静, 谢 政专, 滕 晓丹, 4, 5, 6, *

（1.广西大学土木建筑工程学院, 广西南宁 530004；2.华蓝设计（集团）有限公司, 广西南宁 530011；3.广西交科集团有限公司, 广西南宁 530007；4.广西大学广西防灾减灾与工程安全重点实验室, 广西南宁 530004；5.广西大学工程防灾与结构安全教育部重点实验室, 广西 南宁 530004；6.广西新发展交通集团有限公司, 广西 南宁 530028）

工程水泥基复合材料（ECC）是一种耐磨性、 抗剥落性能、耐久性能、自愈合性能和微裂缝控制能力等各项性能良好的纤维增强水泥基复合材料[1-3］.目 前, ECC较 常 用 的 纤 维 是 表 面 涂 油 处 理的日产聚乙烯醇（PVA）纤维[4］, 但其价格昂贵.为降低ECC的制造成本并推广其应用, Yu等[5］采用聚乙烯（PE）纤维制备了平均拉伸应变能力达到8%的超高性能ECC；Li等[6］采用PE纤维成功制备了极限拉应变大于9%, 并具有饱和多缝开裂行为的高强高延性ECC.为进一步降低ECC的成本, 推广其工程应用, 已有研究采用海砂代替硅砂制备ECC[7］.纤维类型及其掺量会影响ECC的拉伸、微裂缝控制等关键性能及应变硬化指数, 但现有海砂ECC的研究尚未明确不同纤维及其掺量对ECC拉伸性能的影响规律.因此, 有必要深入探讨纤维类型及其掺量对海砂ECC拉伸性能的影响机理.

单轴拉伸应力-应变关系可反映ECC各个受力阶段的破坏过程和变形特点, 是ECC最基本的本构关系, 也是研究其结构承载力和变形的重要依据[8］.Kanda等[9］对PVA纤 维 增 强ECC（PVA/ECC）提出了仅考虑弹性阶段和应变硬化阶段的双线性模型.张聪等[10］研究了钢纤维与PVA纤维混杂增强应变硬化水泥基复合材料（SF-PVA/SHCC）, 提出了适用于SF-PVA/SHCC的单轴拉伸三线本构模型.Li等[11］对PVA/ECC提出了应变硬化材料拉伸应力-应变三线性模型.虽然国内外学者提出了多种ECC拉伸本构模型, 但尚未形成统一的认识, 对于海砂ECC的简化拉伸本构模型也鲜有研究.

本研究团队制备了海砂工程水泥基复合材料（SECC）[12-13］, 已探讨了偏高岭土掺量、骨料形态及粒径对SECC单轴拉伸性能的影响, 并在SECC中采用偏高岭土很好地固化了海砂中的氯离子.本文在前期研究的基础上, 继续探讨PE/PVA纤维及其体积分数对SECC基本力学性能的影响, 并建立了适用于SECC的拉伸本构模型.

1 试验

1.1 原材料

水泥为海螺牌P·O 42.5水泥；辅助胶凝材料为河南某火电厂提供的Ⅰ级粉煤灰、偏高岭土、硅砂, 粉煤灰的中位粒径为13.0 μm, 需水量比（质量比, 文中涉及的组成、比值等除特殊说明外均为质量分数或质量比）0.92, 偏高岭土的中位粒径为6.5 μm, 硅砂的中位粒径为68.0 μm.水泥、粉煤灰和偏高岭土的化学组成见表1, 粉煤灰、偏高岭土和硅砂的粒度曲线见图1.根据GB/T14684—2011《建设用砂》, 测定海砂中氯离子含量为0.21%, 贝壳颗粒含量为4.40%, 细度模数为2.43, 其最大粒径为2.200 mm, 粒径1.250～2.200、0.630～1.250、0.315～0.630、0.160～0.315 mm海砂的含量分别为5.70%、45.30%、42.60%、6.40%.减水剂采用固体聚羧酸系高效减水剂, 减水率为35%, 掺量为0.3%.

表1 水泥、粉煤灰和偏高岭土的化学组成Table 1 Chemical compositions of cement, fly ash and metakaolin w/%

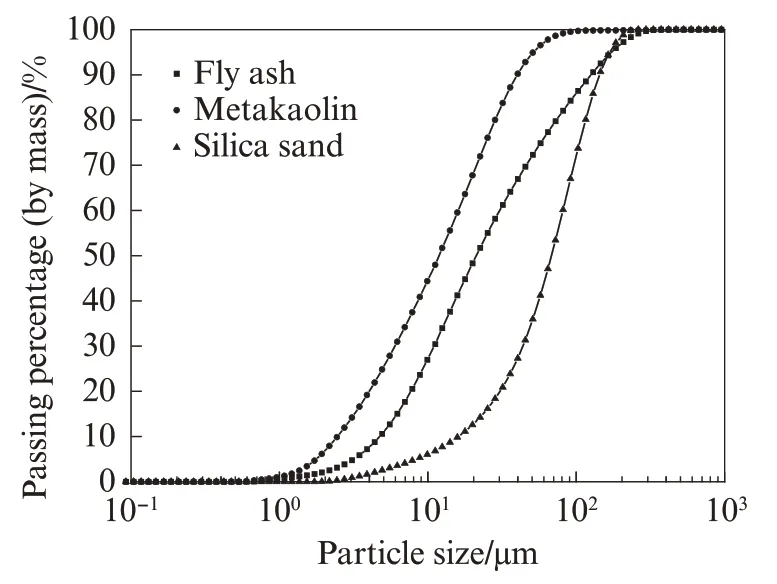
图1 粉煤灰、偏高岭土和硅砂的粒度曲线Fig.1 Particle size distributions of fly ash, metakaolin and silica sand

PVA纤维为日本生产的REC-15, PE、PVA纤维的物理和力学性能见表2.SECC试件的配合比m（水泥）∶m（粉煤灰）∶m（偏高岭土）∶m（硅砂）∶m（海砂）∶m（水）=281∶898∶56∶180∶270∶315.根据JGJ/T70—2009《建筑砂浆基本性能试验方法标准》, 测试了尺寸为70.7 mm×70.7 mm×70.7 mm SECC试件的28 d抗压强度, 加载速率为0.3 MPa/s.SECC中纤维的体积分数, 28 d抗压强度和流动度见表3（表中φPE、φPVA分别为PE、PVA纤维的体积分数）.下文PE/SECC、PVA/SECC分 别 表 示PE纤 维 海 砂ECC、PVA纤维海砂ECC.

表2 PE、PVA纤维的物理和力学性能Table 2 Physical and mechanical properties of PE and PVA fiber

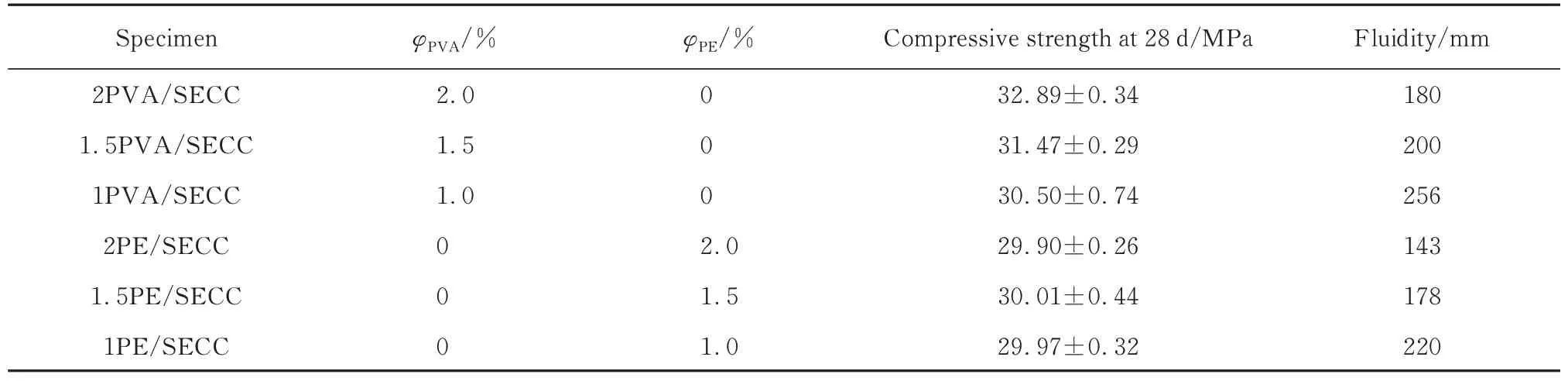
表3 SECC中的纤维体积分数、28 d抗压强度和流动度Table 3 Fiber volume fraction, compressive strength at 28 d and fluidity of SECC

1.2 单轴拉伸试验

用单轴拉伸试验测试SECC的应变能力, 试件为矩形薄板试样, 其尺寸为400 mm×100 mm×15 mm.为使夹具更好地夹紧试件, 并避免夹持部分产生应力集中, 在试件两端采用环氧树脂胶粘贴1层碳纤维增强复合材料（CFRP）布及铝板（CFRP布可提高试件与铝板间的黏结）, 单轴拉伸试验试件示意图见图2.试验采用位移控制加载方式, 加载速率为0.2 mm/min.每组均制备3个试件, 结果取平均值.试件的制备过程为：先将胶凝材料与砂按配合比称量好后, 放入搅拌桶中手动干拌1 min, 使其混合均匀；接着加入水, 并用容量为5 L的JJ-5型搅拌机搅拌2 min；然后加入高效减水剂搅拌, 直至浆体呈现出较好的流动性；再边搅拌边缓慢加入纤维, 搅拌5 min；搅拌完成后, 根据GB/T 2419-2005《水泥胶砂流动度测定方法》测定SECC的流动度（结果见表3）；最后在自制模具中浇筑并振捣, 24 h后脱模, 并标准养护28 d.

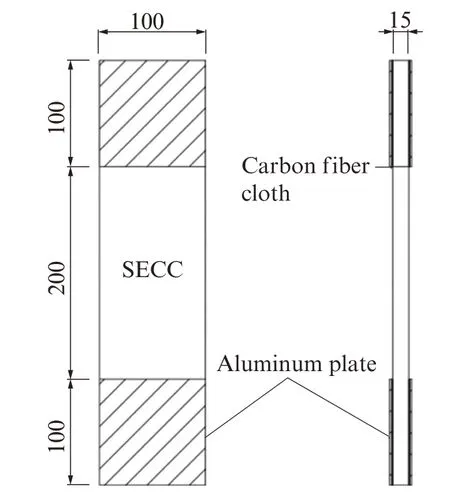
图2 单轴拉伸试验试件示意图Fig.2 Schematic diagram of uniaxial tensile test specimens（size：mm）

2 单轴拉伸试验结果及分析

SECC的拉伸应力σ-应变ε曲线见图3（剔除超过平均值10%的数据）, 其初裂应力σcr、极限拉伸应力σu及极限拉伸应变εu等单轴拉伸试验结果见表4.由图3、表4可见, 不同纤维类型及体积分数的SECC初裂应力不同.影响SECC初裂应力的因素可能有：（1）纤维的体积分数.PE/SECC与PVA/SECC的初裂应力随着纤维体积分数的增加而增大, 而ECC的初裂应力与试件的初始缺陷尺寸、基体断裂韧度有关[14］, 因此这可能是由于纤维体积分数增加, 降低了SECC的初始缺陷尺寸, 从而提高了其初裂应力.（2）纤维表面处理方式.PVA纤维为亲水性纤维, 其表面经过涂油处理（上油量为纤维质量的1.2%）, 这不但利于分散纤维, 且大幅减小了纤维与基体间的化学黏结, 从而增加了纤维/基体间的摩擦黏结, 使纤维更多地发生拔出破坏而非拉伸破坏[15］；对于憎水性的PE纤维, 其在SECC基体中主要依靠自身的高抗拉强度、高弹性模量发挥作用, PE/SECC的初裂应力比PVA/SECC低, 可能是由于PE纤维/基体间的化学黏结不足或纤维团聚导致, 后文将通过扫描电镜（SEM）进一步论证.

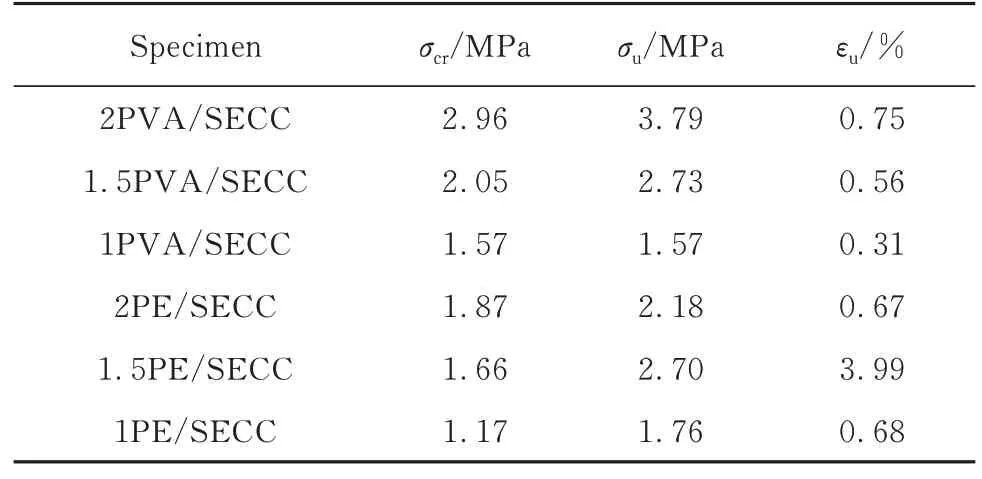
表4 SECC的单轴拉伸试验结果Table 4 Results of uniaxial tensile test of SECC

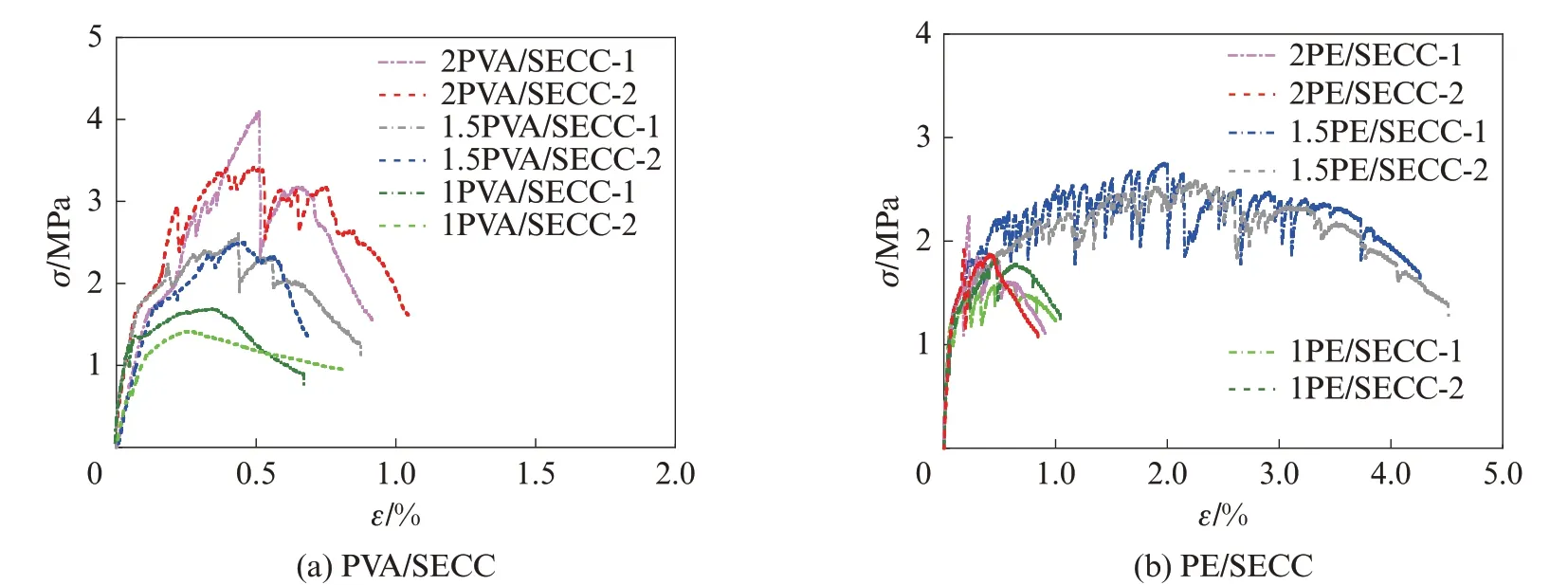
图3 SECC的拉伸应力-应变曲线Fig.3 Tensile stress-strain curves of SECC

对于PVA/SECC：PVA/SECC的极限拉伸应力、极限拉伸应变均随PVA纤维体积分数的降低而降低, 这是由于PVA/SECC的流动度随纤维体积分数的增加而降低（见表3）, 且PVA/SECC的流动度比PE/SECC的流动度高出12.4%～25.9%, 这是由于PVA纤维表面经涂油处理, 在其体积分数为1.0%～2.0%时不存在分散性问题, 因此PVA/SECC的拉伸性能与纤维体积分数呈正相关；当PVA纤维体积分数降低至1.0%时, 由于纤维桥接能力不足, PVA/SECC失去了应变硬化行为, 破坏时仅有单条裂纹（见图4（a））；与2PVA/SECC和1.5PVA/SECC相 比, 1PVA/SECC的 极限拉伸应力分别下降了58.6%、42.5%, 极限拉伸应变分别下降了58.7%、44.6%, 两者下降幅度相近.

图4 SECC破坏形式Fig.4 Failure modes SECC

SECC拉伸断面的SEM图见图5.由5可见：1PVA/SECC的破坏截面中, PVA纤维均为拉伸破坏；2PVA/SECC与1.5PVA/SECC的破坏截面中, PVA纤维拔出破坏与拉伸破坏同时存在.由此可知, PVA纤维数量不足, 会导致其破坏形式由部分拉伸破坏变为全部拉伸破坏, 从宏观上表现为单裂纹破坏.

对 于PE/SECC：2PE/SECC和1PE/SECC的抗拉强度、延性十分接近, 极限拉伸应变仅相差0.10%；1.5PE/SECC表现出了饱和多裂缝开展的应变硬化行为（图4（b））, 其极限拉伸应变达到3.99%, 与2PE/SECC和1PE/SECC的极限拉伸应变相比提高了约487.00%, 这是由于PE纤维为憎水性纤维, 当其体积分数为2.0%时, 在浇筑时较难分散, 导致其在基体中产生了团聚现象（见图5（d））, 使真正能发挥桥接作用的纤维数量与其体积分数为1.0%时相近（图5（f））；由于PE纤维自身高强度高弹性模量的特点, 其在基体中的破坏均为拔出破坏（见图5（c））；破坏截面的PE纤维数量随纤维体积分数的减少而减少.1.5PE/SECC的流动度与2PVA/SECC的流动度最接近, 仅相差约12.4%, 故其在分散性及纤维数量方面均可达到最优, 使其拉伸性能最好.

图5 SECC拉伸断面的SEM图Fig.5 SEM images of tensile section of PE/SECC specimens

3 SECC拉伸本构模型

3.1 SECC拉伸应力-应变关系分析

由图3可知, 具有应变硬化行为的PVA/SECC、PE/SECC的破坏模式呈现三阶段特征：（Ⅰ）线弹性阶段SECC的拉伸应力-应变曲线呈线性关系, 试件表面无裂缝产生；（Ⅱ）稳态开裂（应变硬化）阶段 随着荷载的增加, 试件产生第1条裂缝, 在纤维的桥接作用下主裂纹扩展缓慢, 主裂纹扩展的同时, 其他部位产生多条细密裂缝, 在拉伸应力-应变曲线上表现为波动上升；（Ⅲ）软化阶段 拉伸应力-应变曲线不再出现波峰, 并缓慢下降（PE/SECC）, 试件无法继续承担拉伸荷载, 从主裂纹处破坏.与PE/SECC相比, PVA/SECC的软化段下降更迅速.

3.2 模型建立

以 往 的 研 究[9-10, 16-17］通 常 将ECC的 拉 伸 本 构 模型简化为双线模型（见图6（a））, 该模型将极限拉伸应力σu处定义为试件破坏点, 在此处取极限拉伸应变εu.由于SECC试件的极限拉伸应力σu与极限拉伸应变εu不在同一个点, 故双线模型并不适用.若将该模型用于预测SECC的拉伸应力-应变曲线, 则会造成承载力过剩的问题.以1.5PE/SECC为例（见图6（b））, 将1.5PE/SECC单轴拉伸试验曲线的极限拉伸应力点（2.00%, 2.78 MPa）作为试件破坏点, 则2.00%极限拉伸应变后半段的曲线将作为软化段被忽略, 显然与实际情况不符, 后半段曲线仍具有部分承载力.

图6 ECC的双线模型及其在1.5PE/SECC中的应用Fig.6 Bilinear models of ECC and its application in 1.5PE/SECC

基于上述原因, 本文提出了新的SECC拉伸本构模型：

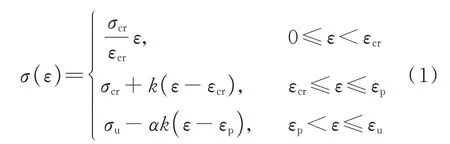
式中：εcr、εp分别为初裂应变、极限拉伸应力对应的应变；k为强化系数,为衰减系数.

3.3 模型参数分析

3.3.1 定义初裂点

进行单轴拉伸试验时, 由于安装夹具及试验机夹头夹紧夹具时可能会造成试件中心轴线偏离加载方向, 导致初始偏心, 造成实测初裂荷载值偏低.因此, 本文将线弹性阶段与应变硬化阶段中的强化段拟合所得直线的交点定义为名义初裂点[18］.

3.3.2 稳态开裂阶段

因试件到达软化阶段时已完全失去承载力, 故在SECC的拉伸本构模型中将其忽略.根据Li[11］的研究, 稳态开裂应力σss由ECC的裂纹桥接应力σc和开裂应力水平σfc估算得到.试件在单轴拉伸荷载下, 在初始缺陷尺寸最大处开裂, 第1条裂纹开裂后, 纤维提供桥接余能, 裂纹桥接应力σc向缺陷尺寸较小处传递, 纤维再提供桥接余能, 如此反复直至主裂纹贯穿整个试件截面, 试件破坏.

本文SECC的裂纹桥接应力σc达到峰值后并未像传统的ECC软化后下降, 而是波动下降, 即仍能产生裂纹并具有一定的承载力.这是由于荷载达到峰值时, 主裂纹仍未贯穿试件横截面, 导致其仍能承担拉伸荷载, 并具有稳态开裂行为, 与峰前拉伸应力-应变关系不同的是, 峰后拉伸应力-应变曲线是波动下降的.这可能是由于荷载达到峰值后, 试件多处纤维发生拔出破坏, 纤维/基体间的摩擦黏结强度τ下降, 导致复合材料的裂纹桥接应力σc下降.

将SECC拉伸应力-应变关系曲线中的应变硬化阶段分为强化段与软化段, 强化段为初裂应力至极限拉伸应力对应的曲线, 软化段为极限拉伸应力对应的应变至极限拉伸应变对应的曲线, 并将其简化为线性关系, 结果见图7（图中σt为SECC极限应变对应的拉伸应力）.SECC拉伸应力-应变关系曲线中的强化段表现为波动上升, 软化段表现为波动下降, 下降趋势较为平缓, 试件具有充足的承载力, 仍能产生多缝开裂行为.强化段引入强化系数k, 表征纤维对SECC拉伸应力的增强幅度；软化段引入衰减系数α, 表征SECC在拉伸荷载作用下达到其极限拉伸应力后, SECC裂纹桥接能力的衰减.SECC强化段、软化段的拉伸本构关系可分别表示为：

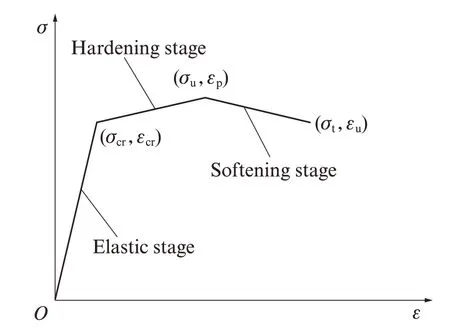
图7 SECC受拉应力-应变曲线简化模型Fig.7 Simplified tensile stress-strain curve of SECC

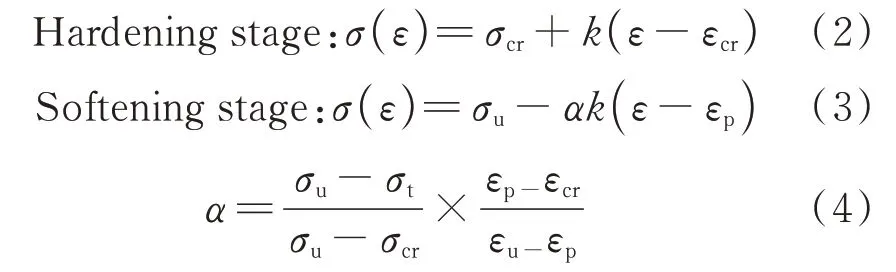
采用最小二乘法对具有应变硬化行为试件的试验数据进行回归分析, 得到k、α, 结果见表5.由表5可见：不同纤维类型及体积分数对SECC拉伸性能的强化程度不同.强化段应变Δε相同的情况下,k值越大, 纤维对SECC强化段拉伸应力Δσ的提升越大；软化段应变Δε相同的情况下,α值越大, SECC在拉伸荷载作用下达到其极限拉伸应力后, 其软化段拉伸应力Δσ衰减越快.对于PVA/SECC, 其最优纤维体积分数为2.0%, 故建议取k=531.97,α=0.494；对于PE/SECC, 其最优纤维体积分数为1.5%, 故建议取k=44.49,α=0.477.在本文研究范围内, 强化系数随纤维体积分数的减小而减小, 衰减系数随纤维体积分数的减小而增大.而1.5PE/SECC的强化系数小于1PE/SECC, 这可能是由于其初裂应力较高, 导致其强化段较为平缓, 也正因如此, 其强化段的总应变增大, 即微裂纹数量增多, 形成稳态开裂, 使其最终的极限拉伸应变增大, 这与前文的试验结果相一致.

表5 强化系数k和衰减系数α的取值Table 5 Values of strengthening coefficient k and attenuation coefficient α

3.4 模型验证

为验证本文提出的SECC拉伸本构模型, 将模拟拉伸应力-应变曲线与试验曲线进行对比, 结果见图8；将初裂应力、极限拉伸应力的计算值T与试验值C进行对比, 结果见表6（表中R=T/C）.由图8、表6可见：本文提出的SECC拉伸本构模型可较好地预测其拉伸应力-应变关系.

由于2PVA/SECC和2PE/SECC的初裂点与极限拉伸应力对应的点十分接近, 2PE/SECC-2的初裂点甚至与极限拉伸应力点重合（见图8（c））, 即强化段应变过小（Δε趋近于0）, 故其初裂应力的计算值误差较大（见表6）, 无论是双线模型还是三线模型, 均不适用于这些试件.这是由于其极限拉伸应变均远小于ECC对极限拉伸应变为2.00%的基本需求, 极限拉伸应变过低, 虽然试件能产生小范围（0%～0.75%）的应变硬化行为, 但在强化段难以形成稳态开裂, 故难以依靠软化段来提高其延性.综上所述, 本文提出的SECC拉伸本构模型可用于反映单轴拉伸荷载下具有稳态开裂行为SECC的拉伸应力-应变关系.

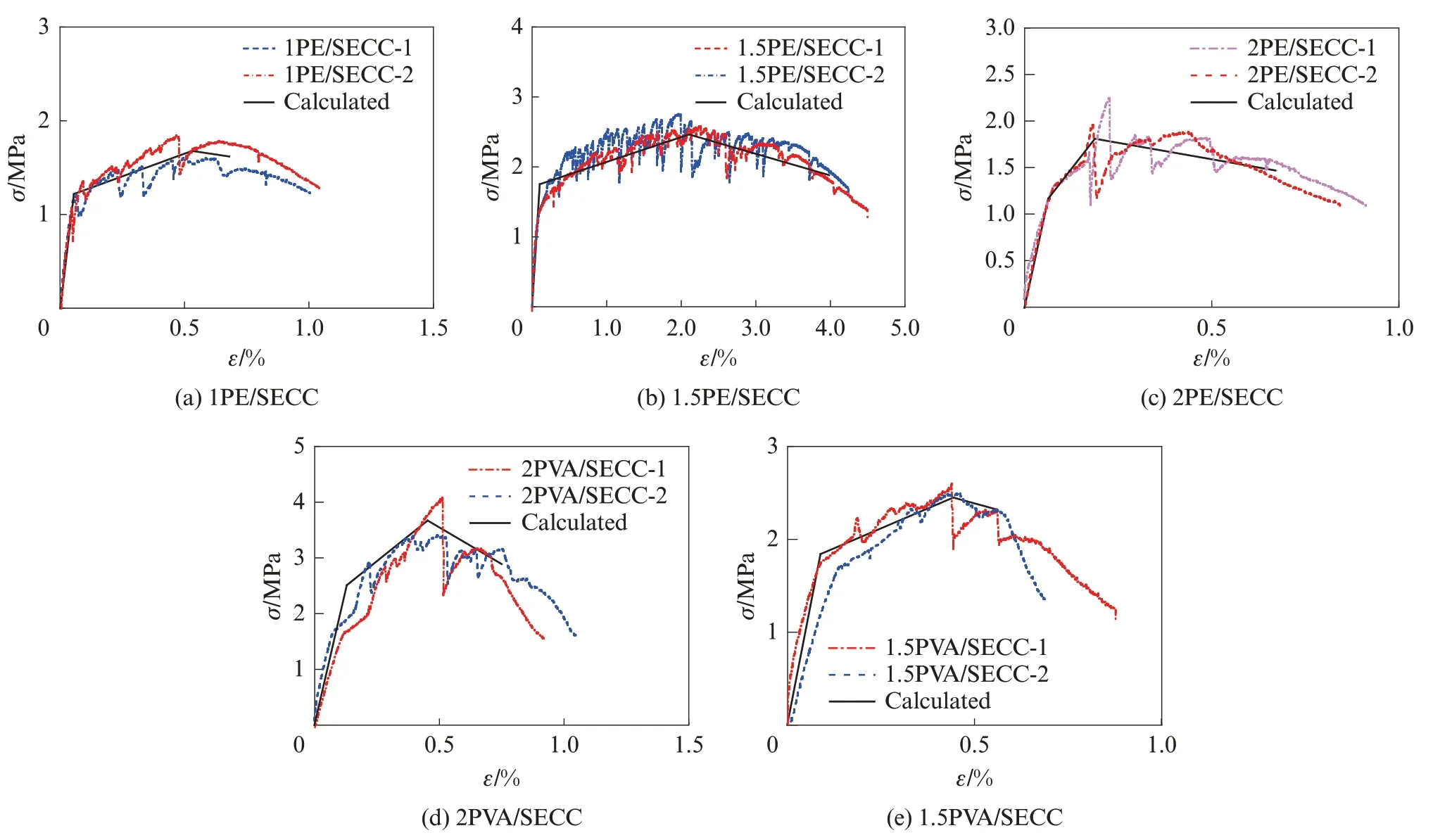
图8 SECC拉伸本构模型模拟结果与试验曲线对比Fig.8 Comparison between modified results from tensile constitutive model and test curves of SECC

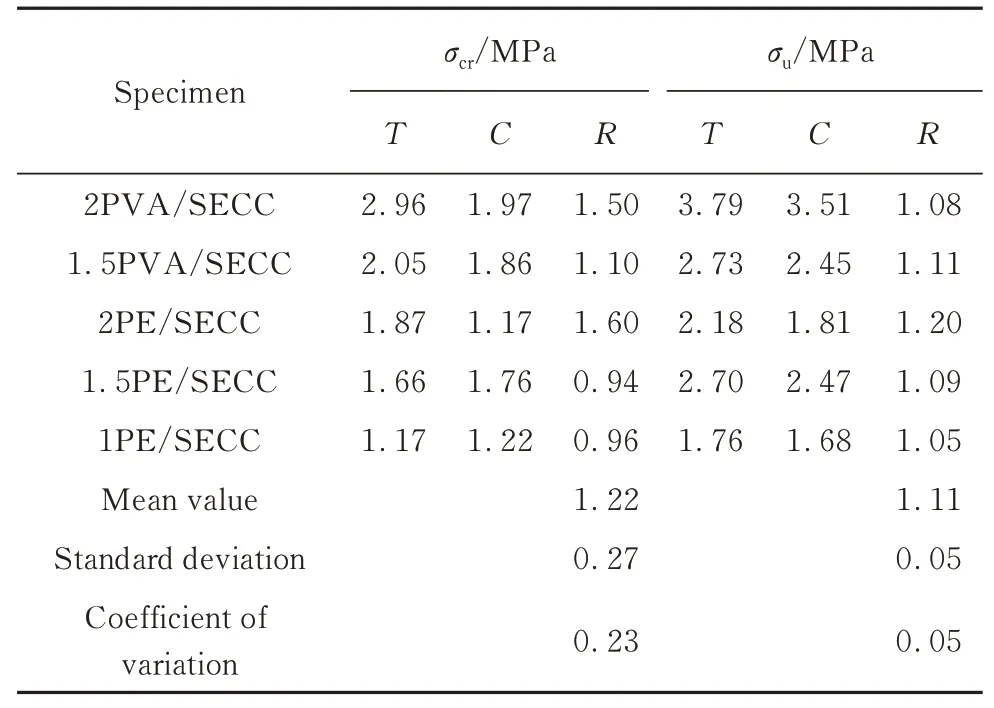
表6 SECC试验值与计算值对比Table 6 Comparison between test values and calculated values of SECC

4 结论

（1）聚乙烯醇（PVA）纤维、聚乙烯（PE）纤维海砂工程水泥复合材料（PVA/SECC、PE/SECC）的最优纤维体积分数分别为2.0%、1.5%.纤维体积分数为1.5%的PE/SECC表现出饱和多缝开裂的应变硬化行为, 延性可达到3.99%, 与2PE/SECC和1PE/SECC相比提高约487.00%.

（2）PVA/SECC与PE/SECC的流动度均随纤维体积分数的增加而降低, PVA/SECC的流动度比PE/SECC的流动度高12.4%～25.9%；纤维体积分数为1.5%的PE/SECC流动度与PVA/SECC的流动度最接近.

（3）本文提出将SECC应变硬化阶段分为强化段与软化段, 以解决传统ECC双线模型在SECC中应用所造成的承载力过剩问题.建立的SECC拉伸本构模型与试验结果基本吻合, 但该模型不适用于无稳态开裂行为的SECC.