面向GPU的非结构网格有限体积计算流体力学的图染色方法优化*
2022-10-05郭晓虎杜云飞卢宇彤
张 曦,孙 旭,郭晓虎,杜云飞,卢宇彤,刘 杨
(1. 中山大学 计算机学院(软件学院), 广东 广州 510006;2. 哈璀国家超算中心 达斯伯里实验室, 英国 沃林顿 WA4 4AD; 3. 中国空气动力研究与发展中心, 四川 绵阳 621000)
非结构网格有限体积方法在航空航天、海洋环境等许多科学计算领域得到了广泛的应用,形成了一些优秀的数值模拟软件,例如OpenFOAM[1]、FUN3D[2]、Fludity[3]、NNW-PHengLEI(风雷)[4]等。随着高性能计算技术的发展,科学计算进入“E级”时代,数值模拟软件的计算性能也不断提高。特别是通用图形加速器(general purpose graphics processing unit, GPGPU)的快速发展,计算能力强、功耗低的GPU在科学计算中起到了越来越重要的作用。如何充分利用GPU,提高非结构网格有限体积数值模拟的计算性能,已经成为高性能计算领域的重要课题之一。
GPU性能的发挥主要取决于硬件占用率和访存延迟。非结构网格的数据存储是不规则的,需要通过几何拓扑关系访问数据,例如通过面循环访问体变量,这将导致频繁的不规则内存访问,增大访存延迟。因此,如何利用GPU多级存储体系减小访存延迟是提高应用性能的关键。
几何拓扑依赖读写模式在多线程并行计算中,可能造成多个线程改变相同的全局内存或共享内存,导致错误的计算结果,即资源竞争问题。图染色[5]是解决资源竞争问题的一种重要方法。该方法将发生冲突的面通过染色分成若干组,以保证每一组中的任何两个面都不会更改相同的体变量。多线程并行计算可以在每一组中正确地实现。
图染色方法在可移植性和计算性能方面具有优势。图染色方法通过常规的编程语言即可实现,几乎可以移植到任何一种硬件平台。一些学者在有限元、有限体积计算流体力学(computational fluid dynamics, CFD)的实际案例中发现图染色方法具有较好的性能[6-7]。FUN3D[8]和SU2[9]也采用了图染色方法解决多线程计算中的资源竞争问题,但都集中于CPU。本文讨论了图染色方法对于GPU计算性能的影响。
图染色方法在分组之后,每一组的计算仍然存在不规则访存的问题,需要进一步优化。Giuliani等[10]针对简单的几何拓扑关系,提出了一种优化方法,但无法将其应用在未知量定义在体中心的计算。Sulyok等[11]也提出了优化方法,但是只针对一种网格尺寸进行了性能分析。本研究的图染色方法可应用在多种规模的复杂三维非结构网格。
1 非结构网格有限体积CFD数学模型
本研究采用的非结构网格有限体积CFD程序是NNW-PHengLEI(风雷)。该程序由中国空气动力研究与发展中心研发。
1.1 控制方程与离散
控制方程为积分形式的NS(Navier-Stokes)方程,表示为
(1)
其中:Fc和Fv分别为对流通量和黏性通量;Q包含5个未知数,可以表示为

(2)
式中,ρ表示流体密度,u、v、w分别表示速度在x、y、z三个方向的分量,e表示内能。 这些物理量定义在控制体Ω中心上。
有限体积方法将物理空间划分为许多小的控制体(volume),体的边界称为面(face)。相应地, NS方程的离散形式可以表示为
(3)
式中:Ωvol表示控制体的体积;控制体拥有NF个面,每个面的面积为Sm;对流通量Fc采用Roe格式计算,并且采用限制器抑制激波产生的数值振荡;黏性通量Fv采用中心差分格式计算;Splart Allmaras方程湍流模式用来计算湍流的影响;显格式龙格库塔方法用来离散时间项;最终通过对流通量和黏性通量的残差来更新Q,保证计算的收敛。程序在一个时间步的流程如图1所示。

图1 程序在一个时间步的流程Fig.1 Flow chart in one time step
1.2 网格拓扑和数据结构
非结构网格几何拓扑关系由体编号和面编号来表示。非结构网格通常采用面的编号顺序来存储体编号。例如将每个面对应的较小的体编号存储在owner中,将较大的体编号存储在neighbor中。如图2所示,编号为O和P的2个体(O 图2 几何拓扑关系:体和面Fig.2 Geometry topology: volume cell and face 有限体积CFD程序中,变量ρ、u、v、w、e等存储在体中心,称为体数据;对流通量Fc和黏性通量Fv等变量则存储在面中心,称为面数据。体数据和面数据由各自的编号索引,并以结构体数组(structure of array,SOA)方式存储。 非结构网格的几何拓扑关系和数据存储方式使得体数据可以由体编号直接索引,也可以由面编号间接索引。例如表示残差的体变量res,其编号O的数据可以表示为res[O]或者res[owner[f2]]。 在NNW-PHengLEI(风雷)程序中,绝大多数的体数据以1.2节中提到的间接索引方式,通过面循环实现对体数据的修改,从而导致多个不同的面对同一个体数据进行修改。在GPU计算中,多个线程对应的面很可能同时对相同的体数据进行修改操作,导致错误的计算结果。这类计算需要首先解决资源竞争问题,才能在GPU上得到正确的计算结果。本文统计了需要解决资源竞争问题的计算占比,如表1所示,资源竞争问题的计算时间占总计算时间的50%以上,极大地影响了计算性能。图染色方法可以有效地解决资源竞争问题,需研究其性能及其优化。本文从NNW-PHengLEI(风雷)程序中抽取了两种典型的算法讨论。 表1 资源竞争问题计算时间占总时间的比例 算法1描述了由通量flux(面数据)累加计算残差res(体数据)的过程,属于非定常项计算中的通量累加更新残差计算部分(如图1、表1中的C6所示)。该算法通过遍历所有的面(0~numFaces-1),将面数据flux累加到owner、neighbor间接索引的体变量res。结合图2可见,GPU的多个线程在处理不同的面(f1、f2、f3、f4)时,有可能同时修改res[O],造成资源竞争。 算法1 通量累加计算 算法2描述了局部最大压力plmax(体数据)的计算过程,属于对流通量计算中的限制器计算部分(如图1、表1中C5所示)。该算法通过遍历所有的面,借助owner、neighbor间接索引plmax、ps,完成比较。由图2可知,plmax[O]有可能被GPU处理f1、f2、f3、f4面的多个线程同时修改,造成资源竞争。 算法2 局部最大压力计算 算法1和算法2在GPU计算中的资源竞争问题可以通过图染色方法解决。首先,将存在冲突的面进行染色分组,保证每一组中的任何两个面对应的计算不会修改相同的体数据;其次,将每一组计算分别放在GPU上,并通过全局内存读写的优化,降低访存延迟。 面染色是一个NP完全问题[12]。在计算流体力学应用中,最优的染色结果只存在于简单的二维几何拓扑中[10]。对于复杂的三维几何拓扑,仅能够得到一般的染色结果[13]。本文采用贪婪算法对应用在空气动力学中的复杂三维几何拓扑进行面染色分组。 首先,计算面的冲突关系。位于同一个体中的面相互冲突,计算面的冲突关系就是收集与该面同体的其他面。计算过程中除了利用owner、neighbor,还要利用表征体-面拓扑的变量volFaces、volFacesPosi。volFaces存储了每个体包含的面数量以及面编号;volFacesPosi存储了每个体的拓扑信息在volFaces中的位置。如图2所示,编号为O的体包含编号为f1、f2、f3、f4的4个面。O对应的拓扑信息存储在volFaces中,起始位置为volFacesPosi[O]。O包含的面数量可以表示为volFaces[volFacesPosi[O]]=4,对应的面编号可以表示为volFaces[volFacesPosi[O]+m]=fm(m=1,2,3,4)。因此,在包含f2的编号为owner[f2]=O的体中,存在与f2冲突的面f1、f3、f4;类似地,编号neighbor[f2]=P的体包含的面分别为f5、f2、f6、f7,其中f5、f6、f7与f2冲突。最终,收集f2的冲突关系,包括f1、f3、f4、f5、f6、f7。汇集所有面的冲突关系,存储在变量nfcf、faceConflict、faceConflictPosi中,分别对应冲突面个数、冲突面ID、冲突面的起始位置。f2的冲突信息表示为nfcf[f2]=6,faceConflict[faceConflictPosi[f2]+m] (m=0,1,2,3,4,5)分别对应了f1、f3、f4、f5、f6、f7。具体描述见算法3。 算法3 面的冲突关系计算 接着,利用冲突关系,通过基于贪婪算法的面染色方法将所有面进行染色,避免有冲突关系的面颜色相同,具体描述见算法4。对于编号faceID的面,通过faceConflict[faceConflictPosi[faceID]+m] (m=0, …,nfcf[faceID]-1)遍历所有与faceID冲突的面,根据这些面已经染的颜色判断出面faceID可以染色的最小值。染色的结果存储在变量numFaceGroups和colorFaces中。numFaceGroups表示颜色的种类;colorFaces存储了每个面的颜色。 算法4 基于贪婪算法的面染色 最后,将不同颜色的面分组。利用面染色结果numFaceGroups和colorFaces,将相同颜色的面连续排列,存储在变量faceGroup中。同时记录每种颜色对应的面数量groupNum和每种颜色的面在变量faceGroup中的起始位置colorPosi。 在面染色分组之后,每个组可以分别在GPU上计算。为了提高数据的局部性,减少数据读写的内存访问延迟,分别采用GPU共享内存、体和面编号重排、面数据重排的策略优化图染色方法。 算法5实现了通量累加(算法1)的GPU计算。通过染色分组数量numFaceGroups确定循环次数,将每个分组依次放入GPU进行计算,避免了资源竞争。借助面染色分组信息groupNum、colorPosi,可以得到每个分组对应的面数量numFacesInGroup和分组在faceGroup的起始位置colorStart。接着,GPU线程通过faceGroup得到面编号faceID,再借助owner和neighbor得到相应的体编号ownVolID和ngbVolID,将面上的通量flux[faceID]累加到相应的体数据res[ownVolID]和res[ngbVolID]中。 算法5 通量累加的图染色算法 算法6实现了局部最大压力(算法2)的GPU计算。该算法借助染色分组信息,将分组依次放入GPU计算,避免了资源竞争。GPU线程编号faceInGroupID通过faceGroup和colorStart,实现了与面编号faceID的映射,并通过owner和neighbor,得到相应的体编号ownVolID和ngbVolID。最终,实现了体数据ps[ownVolID]与plmax[ngbVolID]的比较以及ps[ngbVolID]与plmax[ownVolID]的比较。 算法6 局部最大压力计算的图染色算法 在算法5和算法6中,GPU线程根据面编号faceID,通过owner和neighbor间接索引到编号分别为ownVolID和ngbVolID的体数据。ownVolID和ngbVolID很难同时保证体数据读写的对齐。此外,染色分组造成了分组中面数据的非对齐访问。因此,加剧了GPU全局内存访问的延迟。 采用共享内存优化图染色法:针对间接索引带来的体数据无法对齐读取的问题,利用共享内存减小体数据读取延迟,相应的描述在算法7、算法8中。 算法7采用GPU共享内存对通量累加的图染色算法(算法5)进行优化,以减小数据读取延迟。该算法首先在GPU中定义共享内存变量fluxShare。接着,GPU线程先将面数据flux读取到fluxShare中,再将fluxShare累加到体变量res中。 算法7 共享内存优化图染色算法(通量累加) 算法8利用GPU共享内存优化局部最值的图染色算法(算法6),以减小数据读取延迟。该算法先将体变量ps读取到共享内存psShare中,再利用psShare和体数据plmax进行比较。 算法8 共享内存优化图染色算法(局部最值) 针对体数据的非对齐读写,可以通过重排体编号、面编号的策略[14]进行优化。重排后的编号使得面数量最大(即numFaceGroups最大)的分组实现体数据的对齐读写。通过提高数据的局部性,以减少GPU全局内存的访问延迟,相应算法描述在算法9、算法10中。 算法9 体、面编号重排优化图染色算法(通量累加) 算法10 体、面编号重排优化图染色算法(局部最值) 算法9对通量累加的图染色法GPU计算(算法5)进行了优化。与算法5相比,对owner、neighbor、faceGroup进行了重排。重排后的ownerRe、neighborRe、faceGroupRe可以保证体编号ownVolID和ngbVolID在计算量最大分组中的连续性,使得体数据res的读写对齐。 算法10对局部最值的图染色法GPU计算(算法6)进行了优化。通过体、面编号排,实现了面数量最多分组中体数据plmax、ps读写的对齐。 最后,针对面数据的非对齐读取,重排面数据,使得面数据按照染色分组后的面编号重新排列,实现了面数据的对齐读取。相应的描述见算法11。 算法11对通量累加的染色法GPU计算(算法5)进行了优化。面数据flux是按照面标号递增的顺序排列的,但是经过染色分组后,分组中的面编号排序(faceGroup)并不是按顺序的,造成了面数据的非对齐读写。按照faceGroup中的面编号顺序重排flux,得到面数据fluxRe,将fluxRe累加到相应的体数据res中。 算法11 面数据重排优化图染色算法(通量累加) 为了分析图染色及其优化算法的性能,采用ONERA M6外流场CFD计算的三维非结构网格展开性能测试。如图3所示,以正四面体和棱柱体网格填充三维计算域,棱柱体网格存在于M6机翼附近。并采用如表2所示的5种不同网格规模测试算法的性能。 图3 ONERA M6网格Fig.3 ONERA M6 mesh 表2 5种网格规模 算法5~11通过CUDA C实现。原CFD程序可以进行单、双两种精度的计算,因此本文分别针对双精度操作数和单精度操作数进行测试。每个kernel都重复运行1 000次并记录运行时间。 测试平台包括CUDA 10.0驱动的Nvidia Tesla V100 GPU以及CUDA 8.0驱动的Nvidia Tesla K80 GPU。 基于贪婪算法的面染色结果如表3所示,可见所有网格都被分为了8组。混合网格中含有棱柱体,棱柱体网格具有5个面,因此,面染色结果至少存在5个分组。对于复杂的三维几何拓扑,比理想化的分组数量多2~3个分组是可以接受的[15]。 表3 面染色分组 算法5~11对应的GPU kernel在V100上的运行时间如表4和表5所示。 表4 运行时间(V100,双精度) 表5 运行时间(V100,单精度) 算法5~11对应的GPU kernel在K80上的运行时间如表6和表7所示。 表6 运行时间(K80,双精度) 表7 运行时间(K80,单精度) 通过面染色分组,图染色方法可以消除GPU计算中的资源竞争。在面染色分组后,为了提高数据在GPU内存中的局部性,降低内存读写的延迟。针对累加操作,本研究采用共享内存、体编号和面编号重排、面数据重排对图染色方法进行了优化。下面进一步探讨这些优化方法的效果。 为了比较各种图染色方法在通量累加操作中的性能,以未优化的算法5运行时间为分母,得到算法5(未优化)、算法7(共享内存)、算法9(体、面编号重排)、算法11(面数据重排)的运行时间比值。 图4所示为V100的比较结果:共享内存的优化效果不明显,性能提高在5%以内;体编号和面编号重排使得执行时间增大;只有面数据flux重排的优化方法(算法11)有效地减少了运行时间。双精度和单精度的计算结果近似,相比未加优化的图染色方法,面数据重排可以带来20%左右的性能提高。 (a) 双精度 (a) Double precision 图5所示为K80的比较结果,和V100类似,只有面数据重排起到了优化效果:双精度计算的性能提升在15%左右,单精度计算的性能提升在10%左右。 (a) 双精度(a) Double precision 针对体编号、面编号重排造成计算性能下降的结果作了进一步分析。以网格4(392万个体、807万个面)对应的8个染色组为例,分别在未优化(算法5)和体、面编号重排(算法9)2种算法下计时,结果如表8所示。 表8 网格4分组运行时间(V100,单精度) 可见,经过体编号、面编号重排后,第1组的运行时间由0.640 s降低到0.241 s,这与第一组的面数据完全实现对齐相吻合。但是,第2~7组的运行时间全部增加,致使体、面编号重排后的总运行时间超过了未优化算法的运行时间。由此可见,体、面编号重排使得第1组数据的局部性得到提高的同时,恶化了其他几组的数据局部性。 NNW-PHengLEI(风雷)程序中存在一些局部最值操作,同样面临资源竞争问题。针对局部最大值计算,本研究采用共享内存、体编号和面编号重排这两种方法对图染色方法进行优化。 为了比较各种图染色方法在局部压力最大值计算中的性能,以未优化的算法6的运行时间为分母,得到算法6(未优化)、算法8(共享内存)、算法10(体、面编号重排)的运行时间比值。 图6所示为V100的比较结果,共享内存优化方法的效果不明显;体编号、面编号重排使得运行时间增加;未优化的图染色法(算法6)性能最佳。图7显示的K80比较结果与V100结果一致。 (a) 双精度(a) Double precision (a) 双精度(a) Double precision 造成这一结果的原因主要在于局部最值运算仅操作体数据。面循环使得体数据访问的局部性降低。体、面编号重排或者共享内存都未能提高体数据的局部性。 本研究已经完成了NNW-PHengLEI(风雷)程序非结构网格程序的异构开发和优化。图8展示了风雷程序GPU版本在1块GPU(Nvidia Tesla V100)和CPU版本在28个CPU核(Intel Gold Xeon 6132)并行计算的加速比(双精度)。可见,在不同网格规模下,平均加速比达到19。 图8 风雷程序1块GPU计算和28 CPU核计算的加速比Fig.8 Speedup of 1 GPU compared with 28 CPU cores 本文采用图染色方法解决非结构网格有限体积计算流体力学在GPU计算中的资源竞争问题,并采用了共享内存、体编号和面编号重排、面数据重排的优化策略对图染色方法进行优化。通过图染色方法及其优化算法在V100、K80两种GPU上,针对应用在空气动力学中不同规模的复杂三维几何拓扑网格,测试通量累加计算和局部最大压力计算,得到如下结论: 1)对于通量累加计算,面数据重排可以将图染色方法在GPU上的计算性能提高10%~20%;共享内存的优化作用小于5%;体编号和面编号重排在提高1个分组数据局部性的同时恶化了其他分组的数据局部性,造成计算性能下降。 2)对于局部最大压力计算,共享内存和体、面编号重排都无法提高体数据的局部性。 今后,将针对不同的硬件架构,例如AMD GPU、ARM、RISC-V等展开图染色方法进行研究。
1.3 资源竞争



2 图染色算法及其应用
2.1 基于贪婪算法的面染色


2.2 图染色分组计算的GPU算法







3 实验结果与分析
3.1 算例和计算环境


3.2 面染色结果

3.3 算例运行时间




3.4 图染色方法在通量累加计算的性能比较
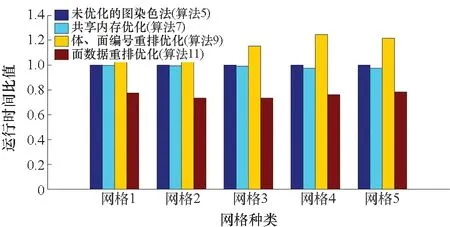


3.5 图染色方法在局部最大值计算的性能比较


3.6 风雷程序GPU计算整体性能

4 结论
