支持工人能力模糊度量和角色协同的软件众包任务分配*
2022-10-05陈跃鹏黄卓轩唐文胜娄小平
马 华,陈跃鹏,黄卓轩,唐文胜,娄小平
(湖南师范大学 信息科学与工程学院, 湖南 长沙 410081)
近年来,以开源众包、任务中国、亚马逊Mechanical Turk和TopCoder等为代表的软件众包平台发展迅速。依托它们,传统的封闭式、高成本、低效率的软件开发过程逐渐呈现出开放式、高性价比、高效率的团体间多人协作的新范式[1]。随着大量众包任务被不断发布,越来越多的软件技术人员以众包工人的角色加入软件众包的协同开发过程。综合考虑工人的历史表现和任务的属性特征以准确度量众包工人的综合能力,实现众包任务和工人间多对多模式下的分配优化,对于确保众包平台获得最佳的整体任务完成质量,具有重要的理论价值和现实意义。
软件众包平台通常采用在线竞争机制挑选优秀的众包工人来承接任务。而工人工作能力的准确度量是众包任务分配前首先需考虑的关键因素,它直接影响到任务的最终完成质量[2]。现有研究尚缺乏对工人能力的全面分析,未综合考虑众包任务与工人能力的匹配程度对分配结果的影响[3],现有的基于单一值的描述机制也无法客观反映工人实际能力的不确定性。同时,现有研究主要采用基于匹配和基于规划的任务分配模型,关注的是面向单个工人的一对一型和一对多型分配问题,尚未涉及面向众包平台的多对多型分配问题[3-4]。
多对多型分配问题从软件众包平台的角度考虑如何将一组相关任务分配给具有协作关系的工人,以获得最佳的全局任务完成质量。由此,多对多型任务分配本质上可视为一个典型的基于角色协同[5](role-based collaboration,RBC)问题。作为RBC的核心模型,E-CARGO[6-7]使用一组核心概念建立组角色分配相关的数学模型,之前基于E-CARGO的任务分配优化研究[8]可为解决多对多型众包任务分配提供重要的求解范式。
基于此,本文提出支持工人能力模糊度量和角色协同的软件众包任务分配方法。该方法通过结合工人的历史表现和任务的需求期望,采用模糊区间数[9]评估工人的多属性能力匹配度,以模糊层次分析法计算工人的综合胜任能力,并引入RBC理论和E-CARGO模型对多对多型任务分配问题进行系统的形式化建模和约束分析,给出了一种有效的问题求解方法,以确保获得最优的整体任务完成质量。
1 相关工作
1.1 众包工人能力的综合度量
众包工人能力度量的传统策略包括基于黄金标准数据的策略[10]、多阶段动态众包质量评估策略[11]、基于熵的众包质量评估策略[12]和基于投票的一次性策略[13]等。并且,基于历史数据对工人进行信誉评估,有助于全面了解工人的综合能力。芮兰兰等[14]引入惩罚激励因子来处罚恶意工人和激励理性工人提高任务完成质量。借鉴滴滴出行软件中司机服务的星级评价,冉家敏等[15]将空间众包中工人的历史等级评价转化为服务质量评价,综合当前评价和历史评价来计算工人得分。针对众包全景拼接系统特点,李沁雅等[16]通过量化街景图像对全景地图构建的贡献度来确定图像质量,以此评估工人能力,并将其与工人酬劳相结合来激励参与者。
现有研究主要使用单一的确定值描述工人的能力。但是,软件技术人员在实施不同项目时,可能受到物质或精神激励、情绪、知识储备和技术成熟度等诸多影响,工作表现并不稳定。从而,在度量工人的综合能力时,不能忽视其具有的不确定性本质。
1.2 众包任务的分配方法
众包模型主要可分为两类:①基于社会网络的复杂任务群智协同众包模型[4]。它不要求发包者自己分解一个复杂任务,而是由接收任务的工人通过组织其合作者来一起完成任务。可免除发包者的任务分解负担,但增加了模型相关的计算量和对工人社会属性深度挖掘的复杂性,实际应用时仍有诸多问题需解决。②基于任务分解的复杂任务众包模型[17]。它要求发包者具备良好的任务分解能力,也要求工人提交的结果具有良好的兼容性。综合考虑可行性和时效性,实际众包应用平台大多采用该模型。
基于任务分解的复杂任务众包模型又可细分为两类:①基于匹配的任务分配模型[3]。它使用二分图匹配,根据任务与工人的时间、空间、状态等特征,并结合工人的信誉值或可信度等,为每名工人分配一项任务,即一对一型任务分配。Mechanical Turk、猪八戒网等传统众包平台以及滴滴出行、美团众包等空间众包平台均属此类。②基于规划的任务分配模型[3]。它类似于旅行商问题模型,研究众包平台如何为一个众包工人分配合理的任务执行顺序和方案,本质上是针对一对多型的任务分配问题,即为一个工人分配多个任务以达到最优的工作组合。考虑到工人的最晚工作时间约束,结合树分解和深度优先搜索方法[18]可获得任务分配最优方案。
随着越来越多的任务被同时发布,众包平台可能存在大量具有相似特点和需求的相关任务。此时的任务分配问题呈现出“多对多”特征,即众包平台如何将多个相关任务分配给合适的多个工人,这是一个NP难问题。不同于传统的一对一或一对多视角,它需要从众包平台整体的角度来考虑如何实现多个任务与工人间的组合优化[3],以帮助众包平台获得全局最佳的任务完成质量。
2 问题描述
假定软件众包平台中某一版块新发布了一个软件开发项目,分解该项目后得到n个待分配任务,以R={r0,r1,…,rn-1}表示任务集(task set),假设在报酬激励下有m个候选工人申请参加该项目,以A={a0,a1,…,am-1}表示工人组(worker group)。则该多对多型软件众包任务分配问题的特点包括:
1) 每个rj(0≤j 2) 不失一般性,假定每个ai(0≤i 3) 同一项目中的不同任务的重要性不同。显然,一些关键任务会相比非关键任务对于项目的完成具有更重要的影响。因此,在任务分配时应为关键任务分配能力更强的优秀工人。 4) 考虑到现实世界中众包工人与任务之间可能存在的各种冲突因素,例如完成任务的时间冲突、合作习惯的冲突以及地理位置的冲突等[1],导致某些工人无法在一起高效地合作开展工作,即工人之间可能存在协作冲突,这些工人不能被分配参与同一任务或项目。 5) 结合众包平台上的历史数据,从技能水平、任务完成效率、任务完成质量、平台活跃程度4个指标对ai的能力进行综合评价。其中,技能水平反映工人的软件设计、开发、测试等方面的专业能力熟练程度;任务完成效率体现工人完成任务的时效性;任务完成质量体现工人最终提交的成果的优劣程度;平台活跃程度反映工人的社交和协作意愿。以上每项指标可由多个子指标来进一步刻画。例如,工人技能水平可从岗位(如前端工程师、开发工程师)、应用类型(如移动应用、微信应用)、开发语言(如Java、HTML5)等方面进行精细度量。通常而言,参与任务的工人的综合能力越强,该任务的最终完成质量越高。 6)为确保获得理想的众包任务完成质量并控制好项目成本开支,发包者可分别对参与rj的ai的各个能力指标设定需求期望(或偏好)[19]。需求期望体现了任务对工人能力的阈值要求。例如,一个工人曾独立完成过高难度的任务,但其平台活跃度和任务完成效率偏低,则该工人并不适合参加对协作性、实时性要求较高的任务。现实中,工人的综合能力越强,通常其雇佣成本也越高,因此,有必要遵循“工人能力够用即可”原则来挑选工人,通过合理设定各个任务的需求期望,以兼顾项目的整体经费开支。 综上,多对多型软件众包任务分配问题,就是在满足给定约束的前提下,基于工人的多指标能力评估和任务需求期望分析,建立n个任务和m个候选者之间的映射关系,为各个待分配任务寻找综合能力尽可能优秀的候选工人,并确保为所有任务挑选出来的工人的全局综合胜任度最高,从而争取整个项目获得最优的完成质量。 定义1区间数。设bL、bH是两个实数,如果B=[bL,bH],0≤bL≤bH≤1,则称B为一个区间数。bL和bH分别称为区间的下限和上限。 (1) (2) (3) 由式(3)可计算工人与每个任务在各个评价指标的可能度,并最终得到工人与任务两两之间关于评价指标匹配度的模糊决策矩阵P,Pi,j,k表示第i(0≤i 在实时型或协作频繁型应用等场景下,发包者对工人的各个能力指标的需求存在差异性。模糊层次分析(fuzzy analytic hierarchy process,FAHP)既可减少主观设定权重的偏差,又可避免计算量大且精度不高的问题,适用于解决多指标综合问题[22]。令模糊判断矩阵B=[bi, j]n×n,满足0≤bi, j≤1,n是工人能力指标个数。bi, j是第i个能力指标与第j个能力指标的重要性之比。采用由0.1、0.3、0.5、0.7、0.9构成的五级互补标度[21]确定bi, j。 矩阵B满足bi, j+bj, i=1,bi, i=0.5,B为模糊互补判断矩阵。当满足bi, j=bi, k-bj, k+0.5时,B为模糊一致性矩阵。令bi为模糊互补矩阵中第i行之和,按式(4)[23]将B转换为模糊一致性矩阵。 zi, j=(bi-bj)/[2(n-1)]+0.5 (4) 仅Z=[zi, j]n×n是模糊一致性矩阵,n=4。计算Z中每行的和,并进行标准化处理,按式(5)获得工人能力指标的权重向量W=[w1,w2,…,w4]。 (5) 基于能力指标的权重向量,最终可获得各个ai完成rj的综合胜任度,计算方法如式(6)所示。 (6) Qi, j表示工人ai对于任务rj的综合胜任能力,该值越大,说明此工人对于该项任务的胜任力越强,则将来可以获得更高的任务完成质量。 借鉴E-CARGO模型[6-8],多对多型软件众包任务分配问题可抽象为:∑::=〈E,C,O,R,A,G〉。 其中:E表示一个涉及多个工人和多个任务的问题环境environment;C是E中抽象概念的类(class)集合;O是与C相关的具体对象(object)集合;R是待分配的任务集合,它对应RBC中的role;A是候选的工人集合,它对应RBC中的agent;G是工作组(group),即由任务分配算法建立的工人团队。 令m=|A|表示候选工人的数量,n=|R|表示待分配的众包任务的数量。 模型中的关键组件包括: 1) 工人综合能力评估矩阵Q:它表示工人ai对于待分配任务rj的胜任程度。 工人的综合能力可通过工人的技能水平、历史任务完成效率和完成质量、平台活跃程度等因素[1]来衡量,Q的计算方法如式(7)所示。 2) 任务分配矩阵T:Ti, j∈{0,1}(0≤i 3) 工作组性能ρ:所有被分配了任务的工人形成一个工作组G。ρ表示G中所有工人的能力值总和。ρ越大,表示所有任务的完成质量越高。对于一组软件众包任务,需要最大化发挥工人的能力,以确保所有任务的ρ最高。 因此,一个任务并不一定被分配给一个胜任力最强的工人。 2) 任务的工人数量需求向量L:Lj表示任务rj需要的最少工人数量。 如果Lj≥1,表示任务rj需要多个工人协作来完成此项众包任务。 为提高任务分配的效率和成功率,在任务分配时需要避开以上可能存在冲突的分配组合。 基于以上定义,可以得到基于角色协同的众包任务分配问题的目标函数: (7) 它应该满足以下条件: Ti, j∈{0,1} 0≤i (8) (9) (10) (11) (12) (13) (14) 其中:约束(8)表示工人是否被分配;约束(9)表示每个任务被分配的工人数量满足该任务所要求的人数限制;约束(10)表示工人只能承接一项任务;约束(11)和约束(12)表示存在冲突的两个工人不能被分配在同一个任务或同一个项目中;约束(13)和约束(14)表示一个工人与其他工人或任务间只存在有冲突与无冲突的两种状态。求解基于角色协同的众包任务分配问题就是要建立一个可以获得最大工作组性能ρ的候选工人集合。 以上众包任务分配问题的求解过程如下: Step1:从众包平台获取工人能力评价的相关原始数据、发包者对工人的能力期望D、任务的下限向量L以及冲突矩阵CA和CR等。 Step2:将工人能力评价的原始数据按3.2节介绍的方法转换为区间数U。 Step3:比较工人能力与待分配任务的需求期望区间数,按3.3节的公式计算工人与任务间关于评价指标匹配度的三维模糊决策矩阵P。 Step4:基于3.4节的介绍,使用FAHP方法计算工人能力指标的权重向量W。 Step5:使用3.5节的式(6)和W计算得到各个ai完成rj的综合胜任度,从而获得候选工人的综合能力值矩阵Q。 Step6:根据给定的Q、CA和CR,对目标函数求解,得到ρ的最大值和任务分配矩阵T。 Step7:如果T可用,则T为最终的分配方案;否则无解,此时众包平台通知任务发包者对任务要求进行调整,直至获得可行的最优解。 借鉴基于角色协同的任务分配研究[7-8],采用IBM CPLEX优化包求解,实现步骤如下: Step1:确定与CPLEX接口的核心数据结构。CPLEX需要目标函数系数、约束系数、右侧约束值以及上下限等输入参数。使用Q、L和T定义CPLEX中的线性规划问题,Q是目标函数系数,T是变量,Qi, j∈[0,1],Ti, j∈{0,1}。 Step3:设定目标函数和约束表达式。众包任务分配问题的目标函数由矩阵Q和T的一维数组形式和L的线性表达式组成。首先,将Q和T变换成一维阵列:Xi×n+j=Ti, j和Vi×n+j=Qi, j。然后,添加优化目标,调用以下方法:IloIntVar[]X=cplex.intVarArray(m*n, 0, 1);cplex.addMaximize(cplex.scalProd(X,V))。最后,迭代添加约束表达式,以Java代码为例,具体实现方法见算法1。 Step4:调用CPLEX的cplex.solve()方法,根据目标函数和约束条件表达式来计算最大化的ρ值。 算法1 添加约束表达式 假定当前环境下需要9名工人完成5个任务,用R={r0,r1, …,r4}表示任务集,假设有12名工人参加竞标,用A={a0,a1, …,a11}表示候选工人集。用U={u0,u1,u2,u3}表示工人综合能力的评价指标集,u0代表技能水平、u1代表任务完成效率、u2代表任务完成质量、u3代表平台活跃程度。在计算各工人的综合能力后,采用基于角色协同的任务分配方法来最优化分配任务。假定由FAHP方法计算得到的权重值为W=[0.15,0.25,0.50,0.10]。从众包平台获取工人的原始评价数据,转换为区间数值,如表1所示。 表1 候选工人的能力评价 发包者为任务设定的需求期望如表2所示。 表2 各个任务对工人能力的需求期望 由式(3)计算工人能力与任务需求的匹配度模糊决策矩阵。第1个工人的匹配度模糊决策子矩阵数据示例如表3所示。再使用权重W加权求和,获取的如表4所示的工人综合胜任度矩阵Q。 表3 第1个工人的匹配度P0, j, k 现实中可能存在多种冲突,假定工人与任务间的冲突约束CR如下所示: 接下来,利用CPLEX优化包求解,设L=[2,1,3,2,1],得到最优解: 根据以上结果,可得到每个待分配任务对应的众包工人组合,如表5所示。 表5 任务分配结果 综上可知,通过评估候选工人的综合能力,建立基于角色协同的任务分配模型,求解后获得多对多型任务分配方案的目标函数最大值为2.569。 为验证所提方法,采用仿真数据进行实验分析。使用64位Windows 10、Eclipse、Java语言。CPU为Intel Core i5-9600K、4.30 GHz,内存为16 GB DDR 4、3 200 MHz,IBM CPLEX Optimization Studio 版本12.7。借鉴任务分配问题常用的实验设定[6, 8],取n=⎣m/3」或n=⎣m/4」,m从10变化到60、步长为5,执行50次取平均值。 运用所提方法进行任务协同分配前,需搜集众包平台上工人能力的原始评价数据并将它们转换为区间数,再与任务需求期望区间数进行可能度计算,继而通过权重合成后获得工人的综合能力评估矩阵Q。实验分析以上数据预处理过程的时间消耗。考虑到现实中能力指标值很低的工人较少可能竞争到众包任务,设定工人能力和任务需求期望的随机范围为[0.3,1.0],设定n=⎣m/3」或n=⎣m/4」、冲突概率为0.1,实验结果如图1所示。 图1 数据预处理时间分析Fig.1 Analysis of data preprocess time 由图1可知,随着工人数量和任务数量的不断增多,数据预处理所消耗的时间逐渐增加,呈现近似于线性增长的趋势。在任务数为20、候选工人数为60的最大数据规模下,多对多型软件众包任务分配问题的数据预处理时间低于0.07 ms,能够具有较理想的处理性能。 实验设定n=⎣m/3」、冲突概率为0.1。考虑到每个Lj>1的任务可等价为Lj=1的多个相同任务,统一设定Lj=1,j∈{1,2,…,n}。每个步骤中初始化Q、CA、CR,对比本文方法与贪心方法、穷举方法的执行时间,结果如表6所示。 表6 n=⎣m/3」时执行耗时分析 表6中,N/A表示在30 min无法获得最优解。由表5、表6可知,随着工人数量的增加,3种方法的耗时随之明显增加,尤其是穷举方法的执行耗时呈指数增长。在n=⎣m/3」的实验中,当工人数小于等于35、任务数小于等于11时,贪心算法的执行性能明显优于本文方法;但是,随着问题规模的增大,当工人数大于等于40、任务数大于等于13以后,在某些特殊的随机数据情况下,贪心方法的执行时间可能急剧增加,在30 min内无法获得优化解。针对m=40、n=13的情况下进行了深入分析,在多个特殊的随机数据样例(原始数据发布于百度云)下贪心方法与本文方法的耗时对比如表7所示。由表7可知,在问题复杂度较大(即工人数和任务数具有一定规模)时,贪心方法在不同数据样例情况下的执行时间具有不确定性,其原因是,在一些特殊冲突矩阵CA和工人综合能力评估矩阵Q场景下,贪心方法在寻找优化解过程中为了避免冲突情况要进行回溯,而随机生成的冲突矩阵可能导致回溯过于频繁,从而使整体执行时间急剧增加。 对比结果可知,冲突约束下多对多型软件众包任务分配问题求解时,即使在工人数为60、任务数为20的最复杂情况下,本文基于CPLEX的求解方法仅耗时66.9 ms,始终能获得令人满意的执行性能。 表7 执行耗时对比 以穷举法获得的最优解为基准,在不同冲突概率情况下测试本文方法命中最优解的概率。实验设定n=⎣m/3」、Lj=1,j∈{1,2,…,n},冲突概率分别设置为0.1~0.4。结果如图2和表8所示。 图2 命中最优解的概率Fig.2 Hit probability of optimal solution 表8 n=⎣m/3」情况下的精度分析 由图2可知,随着问题规模的增加,命中最优解的概率逐渐下降,当问题规模达到一定程度后,命中率将急剧下降。n=⎣m/3」的实验中,冲突概率大于等于0.2时,m大于等于40以后获得最优解的概率就明显不理想了。实验表明,在固定n/m比值的情况下,工人人数越多、冲突概率越大,则命中最优解的概率越低。 本实验以穷举法的结果为基准,对比本文方法与贪心方法的求解精度。实验设定任务数为5,冲突概率为0.1,工人数量以步长5在[10,60]范围内变动。求解精度值的计算公式为: F=1-(ρ*-ρ)/ρ* (15) 式中,ρ*是穷举法获得的最优的工作组性能值,ρ是其他方法获得的工作组性能值。 实验结果如图3和表9所示。由图3可知,本文方法在较大问题规模情况下均能准确获得最优解,求解精度始终为1。而贪心方法虽然执行性能较高,但无法保证始终获得最优解,尤其在问题规模偏小时,其准确率明显不理想。图3中,当候选工人增多时,贪心方法的精度得以明显提高。 图3 精度对比Fig.3 Comparison of accuracy 表9 精度对比 总体来看,本文方法的整体表现明显优于其他方法,在一定规模的众包任务分配求解时,能保证良好的执行效率,并始终能够确保用户获得最优解。基于本文方法可以提高软件众包的任务完成质量,降低项目的开发风险。 针对工人能力的不确定性和任务属性的多样性,提出一种众包工人综合胜任能力的模糊度量方法。它结合工人的历史记录和任务的需求期望,以模糊区间数表征众包工人的历史表现,从技能水平、任务完成效率、任务完成质量和平台活跃程度4个指标评价工人的综合能力,计算多属性模糊能力匹配度,应用模糊层次分析法获得工人的综合胜任能力。引入RBC理论和E-CARGO模型,将涉及任务集与工人组的多对多任务分配问题形式化建模为基于角色协同的组合优化问题,该模型以工人综合胜任能力为基础,综合考虑任务的权重约束、工人数量需求约束、工人与任务间的冲突约束等,以提高任务分配的效率和成功率,并给出了一种基于CPLEX的问题求解方法。通过案例和实验分析了所提方法的可行性和有效性,所提方法可为软件众包应用提供重要的理论参考和决策基础。未来研究中,将对工人综合能力的动态度量和动态任务分配、包含同步任务的工人多角色协同分配等进行深入探讨。3 基于模糊区间数的众包工人能力度量
3.1 基本定义


3.2 基于历史评价的工人能力模糊度量计算

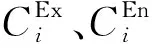

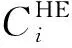
3.3 任务需求期望导向的工人能力匹配度计算

3.4 工人能力评价指标权重的模糊层次分析
3.5 基于能力模糊度量的工人综合胜任度计算
4 基于角色协同的众包任务分配模型
4.1 基本模型
4.2 约束定义
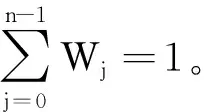


4.3 目标函数
5 众包任务分配问题的求解
5.1 求解过程
5.2 基于CPLEX的求解方法


6 案例分析





7 实验分析
7.1 数据预处理时间分析
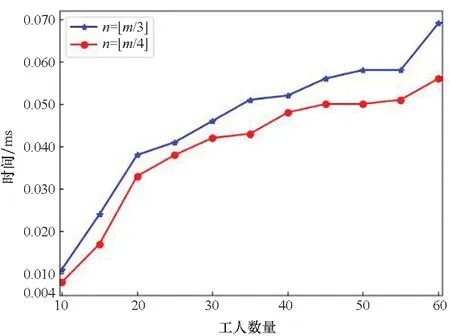
7.2 执行耗时分析


7.3 命中最优解的概率分析

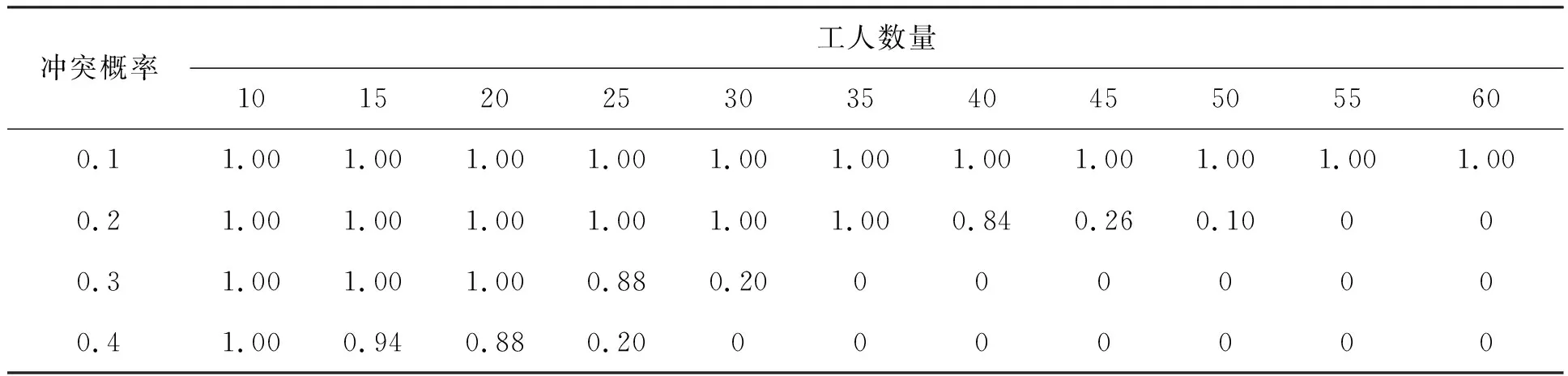
7.4 求解精度分析
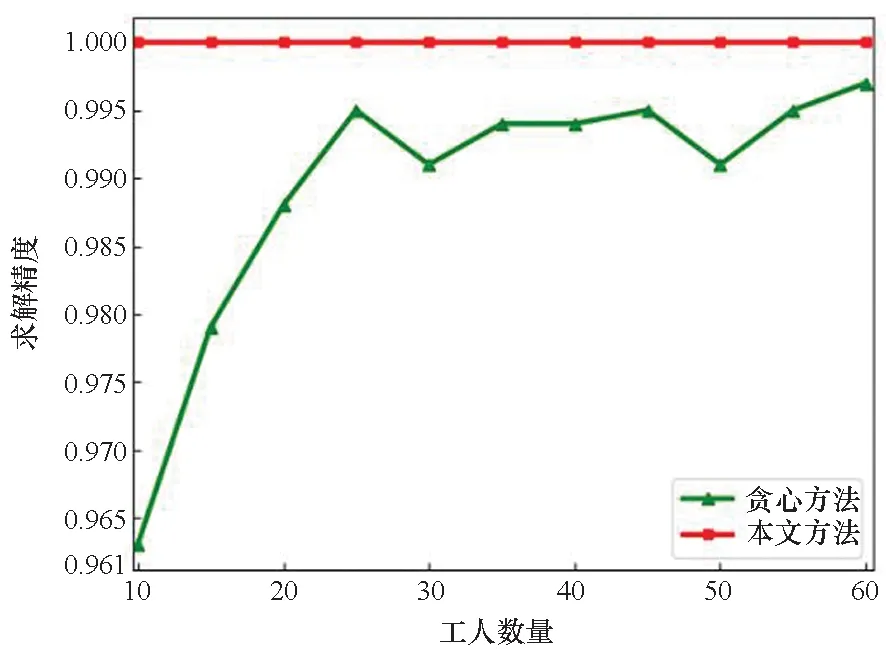

7.5 评价
8 结论
