基于实测车辆荷载的拱桥吊杆疲劳性能研究
2022-10-01庄一舟刘明明董传智
庄一舟,刘明明,董传智
(1.浙江工业大学 土木工程学院,浙江 杭州 310023;2.中佛罗里达大学 土木、环境与建造工程系,佛罗里达 奥兰多 32816)
对于系杆拱桥来说,吊杆是关键的承载构件,它将桥面板自重、车辆及其他外荷载传递给主要受力构件。由车辆载荷和风力载荷引起的周期性应力变化会导致吊杆的疲劳损坏。为了避免吊杆在使用期间发生破坏,相关管理部门一般定期对吊杆进行检查更换,维护费用较高[1]。一般桥梁的设计使用年限为100~120 a,然而在已经更换的拱桥中,吊杆的使用年限仅为3~16 a[2],远低于桥梁的设计寿命。根据《公路钢管混凝土拱桥设计规范》,拱桥吊杆的设计使用年限仅为20 a,然而目前并没有明确的规定或者基于力学的原理来解释这样设置吊杆使用年限的原因。根据现在的拱桥状况,有些拱桥的吊杆使用寿命远远超过20 a,例如,在更换江山市江山大桥吊索时,发现大部分吊索状况良好,表面只存在一点锈蚀。建立服役吊杆的疲劳性能评估方法对桥梁维修中检查和更换的决策至关重要。为了正确地进行吊杆疲劳研究,首先需要一种可靠而有效的方法来获取吊杆的循环拉应力时程。近年来,先进的传感技术已经可以直接用于测量吊杆的张力。例如,He等[3]提出了一种将光纤布拉格光栅(FBG)传感器与布里渊光纤时域分析/反射器(BOTDA/R)传感技术结合在一根光纤中进行吊杆拉力监测的方法;Bao等[4]提出了一种基于自适应稀疏时频分析方法的时变吊杆张力识别新方法;Feng等[5]提出了一种基于新型非接触视觉传感器技术的精确且经济的拉索张力测量方法。这些技术已经证明了传感技术在监测桥梁吊杆不同张力方面的能力。然而将这些传感技术直接应用于拱桥吊杆疲劳研究的报道很少。现有的大多数研究表明交通荷载是桥梁吊杆疲劳损伤的主要原因[6]。近年来,动态称重(WIM)系统收集的车辆荷载数据和有限元模拟相结合的方法开始被应用于桥梁吊杆的疲劳研究。例如,Liu等[7]研究了刚性中心夹对短吊杆疲劳性能的影响,提出了基于车辆载荷模型和从现场监测数据发展而来的风谱的疲劳寿命评估程序。在上述研究中,首先通过使用WIM数据建立了车辆载荷参数的概率分布;然后将通过蒙特卡罗方法生成的随机车辆流应用于有限元模型,以估计吊杆或焊接细节的循环应力的时间历程。这种方法的优点是以相对较小的计算消耗估算车辆载荷对桥梁构件疲劳性能的影响。汪小超等[8]研究了移动荷载作用下桁架桥的动力响应过程;施颖等[9]模拟了轮迹横向分布对异形钢箱梁桥面板4种典型疲劳构造细节的疲劳应力幅的影响,并对其进行了比较。然而,这几种方法不考虑实际车辆载荷的时变特性。
笔者提出了一种适用于组合结构拱桥吊杆疲劳性能研究的框架。不同于其他概率分析方法,笔者利用WIM系统提供的车辆荷载真实信息来重建车辆的荷载流,将重构的车辆荷载应用于有限元分析提取的影响线,将时变车辆荷载转换为吊杆拉力。为了提高计算效率,可采取以下3种措施:将轴重简化为集中力应用于车道的中心线;设置车重阈值(在本研究中为30 kN)以忽略轻型车辆的载荷;在吊杆应力历程计算过程中设置适当的时间步长(在本研究中为0.1 s)。利用雨流计数法提取其中的应力循环,基于Miner线性累积损伤理论评估吊杆的疲劳损伤程度,进而预测其疲劳寿命。
1 桥梁及动态称重系统概况
1.1 桥梁概况
九堡大桥全长1 855 m,桥面为双向行驶,共有6个车道,设计时速80 km/h。桥梁纵横断面布置如图1,2所示。主桥共3跨,采用188 m+22 m+188 m+22 m+188 m的跨径组合布置。上部结构是线路结构,采用结合梁钢拱组合体系拱桥,拱桥主梁为等截面钢混凝土结合梁结构;钢类系统的组成构件包括主副拱肋、主副拱肋之间的横向连杆拱顶横撑以及拱顶横撑等。吊杆上端与下端依次锚固于主拱肋和钢主纵梁。全桥共114根吊杆,为平行钢丝索体系,均为121Φ7 mm。拱桥结构对称,中跨东侧共有19根吊杆,编号由北至南依次为H1,H2,…,H19,其中跨中吊杆编号为H10。中跨东侧吊杆编号见图1。
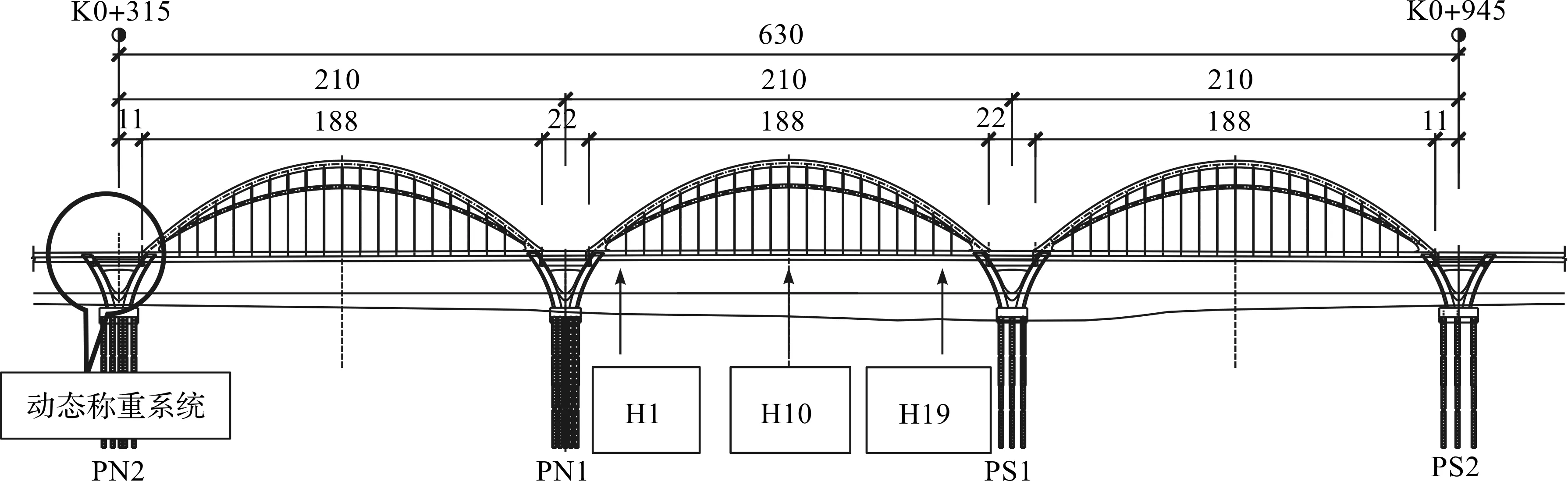
图1 桥梁纵断面布置图Fig.1 Longitudinal section layout of bridge
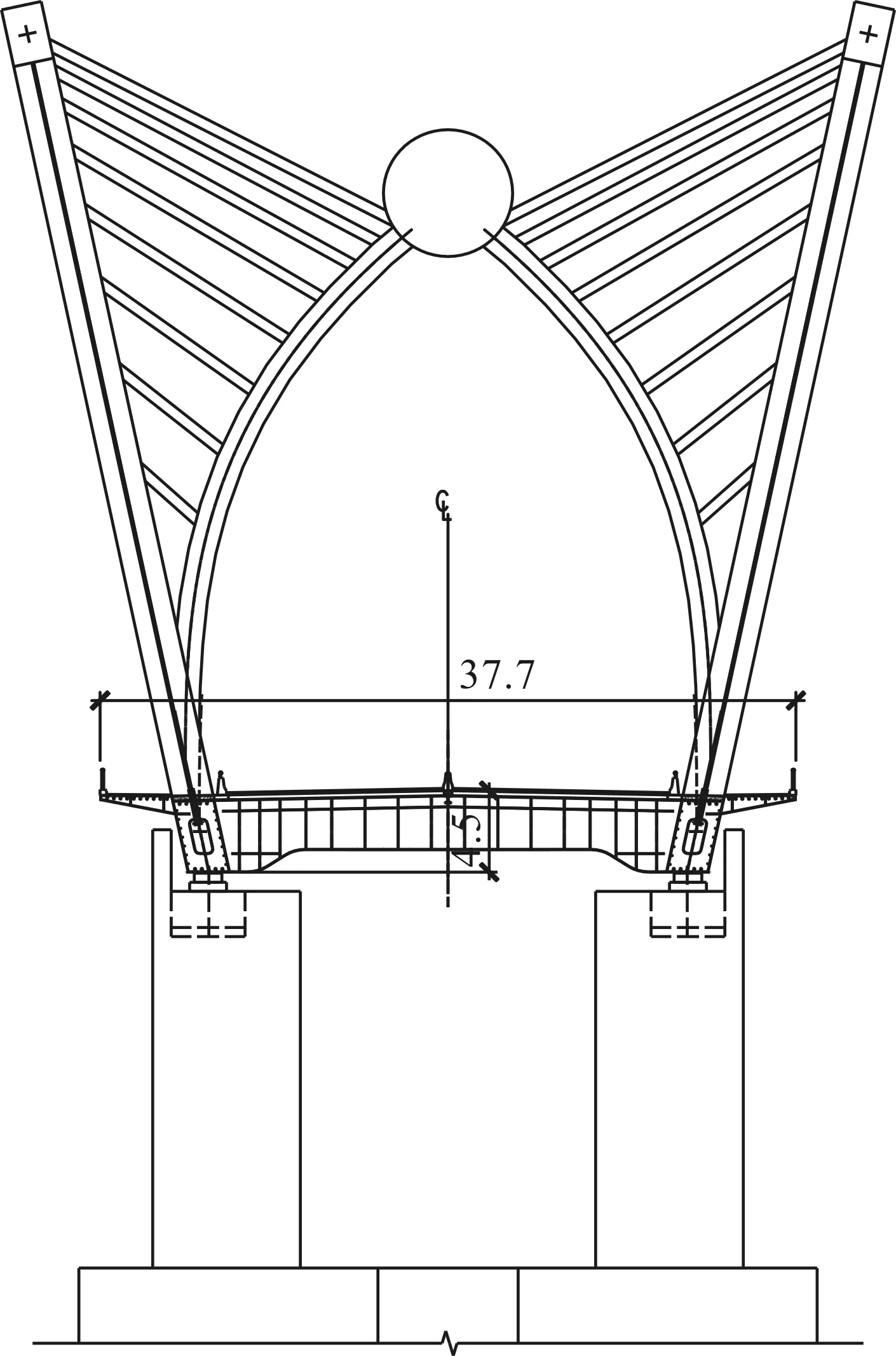
图2 桥梁横断面布置图Fig.2 Cross section layout of bridge
1.2 动态称重系统
九堡大桥结构监测系统由347个传感器组成,其中有风速计、湿度传感器、温度传感器、加速度计、动态称重系统、用于挠度传感的全球定位系统(GPS)、位移传感器、应变计和闭路电视(CCTV)摄像机等。该结构监测系统自动化数据采集的结构响应包括:钢结构、混凝土结构的应力、大桥空间变位和索力变化。其中,动态称重系统(图3)安装在九堡大桥的6个车道的路面上,该系统可以连续实时采集车辆经过时的车流信息,包括车速、车辆横向位置、车流方向、车牌、车型、车辆经过时间、车辆轴型、各轴轴重以及车辆总重等信息。
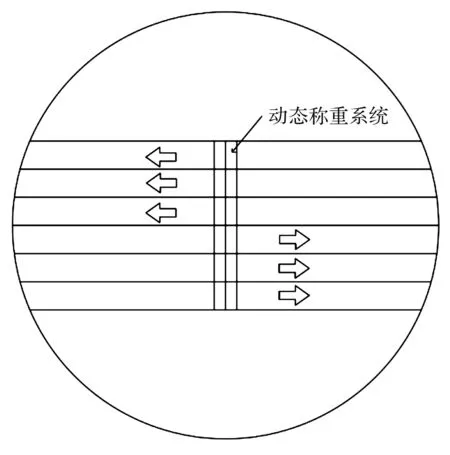
图3 结构监测系统的车辆荷载采集系统安装位置图Fig.3 Installation position diagram of vehicle load acquisitionsystem for structural monitoring system
2 有限元模型
2.1 中跨有限元模型
以中跨为例,采用Midas civil软件建立九堡大桥长为232 m的中跨精细的三维空间有限元模型。根据九堡大桥主桥结构特点,采用梁单元模拟主拱肋和副拱肋,采用杆单元模拟系杆和吊杆,采用板单元模拟桥面板,采用梁单元模拟主梁钢结构部分和钢横梁。在桥面板上逐节点施加一个1 N的集中力,对桥梁中跨进行内力计算分析,可以得到6个车道的影响线曲线。分析结果如图4所示。

图4 边跨影响线曲线Fig.4 Side span influence line curve
2.2 车道影响线
通过Midas civil的内力分析可以得到696个离散点,通过线性拟合现有的影响点可以推导出每个吊杆拉力影响线,结果如图5所示。拉力峰值出现在与吊杆对应的纵向位置。研究发现:车道1~6在1 N荷载下,吊杆H1最大拉力分别为0.087,0.071,0.058,0.038,0.025,0.012 N。

图5 车道影响线Fig.5 Lane influence line
为了将内力分析得到的结果作为计算交通荷载的运算依据,采用傅里叶八阶线性拟合的方法对内力分析得到的离散影响点进行线性拟合。定义桥面系以西往东的方向为X正轴,车道影响线函数可以表示为
f(x)=a0+a1·cos(x·ω)+b1·sin(x·ω)+
a2·cos(2x·ω)+b2·sin(2x·ω)+…+
a8·cos(8x·ω)+b8·sin(8x·ω)
(1)
式中:a1,a2,…,a8,b1,b2,…,b8,ω均为拟合常数。
为了分析傅里叶八阶线性拟合结果的真实性,对6个车道的曲线拟合误差进行了计算,曲线误差计算结果如表1所示。由表1可知:采用傅里叶八阶线性拟合对中跨离散影响点拟合的曲线误差在可接受范围内,可以将此方法得到的曲线函数作为车道影响线函数的结果。
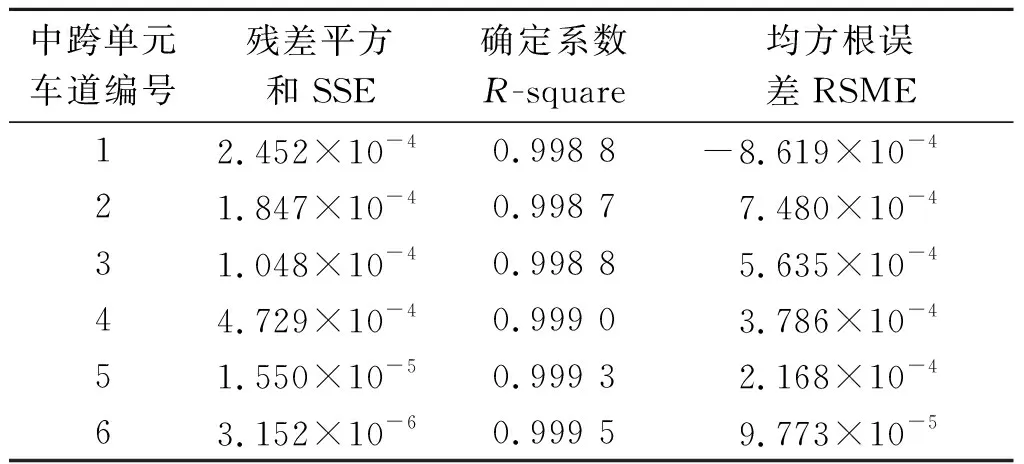
表1 采用傅里叶八阶线性拟合对中跨离散影响点拟合的曲线误差
3 吊杆疲劳性能研究
3.1 车辆加载配置
利用动态称重系统收集的每辆过往车辆的完整信息可以将时变车辆荷载转换为吊杆时间张力历程。首先,选择1 d作为车流数据处理的时间间隔,假设每辆车的速度和车道位置为常数;然后,通过车辆到达时间和速度来确定每辆车在通过桥面的每个时刻的位置;接着,将每辆n轴车简化为n个集中力施加于傅里叶八阶线性拟合的吊杆影响线函数,可以得到单辆车通过桥面时的吊杆应力时间历程;最后,将每天通过的所有车辆的时间应力历程叠加,可以得到不同吊杆从00:00:00—24:00:00的应力时间历程。吊杆H1在2020年6月1日的某一时间段内(15 min)的时间应力历程如图6所示。从图6中可以看到吊杆H1的应力在340~348 MPa波动。
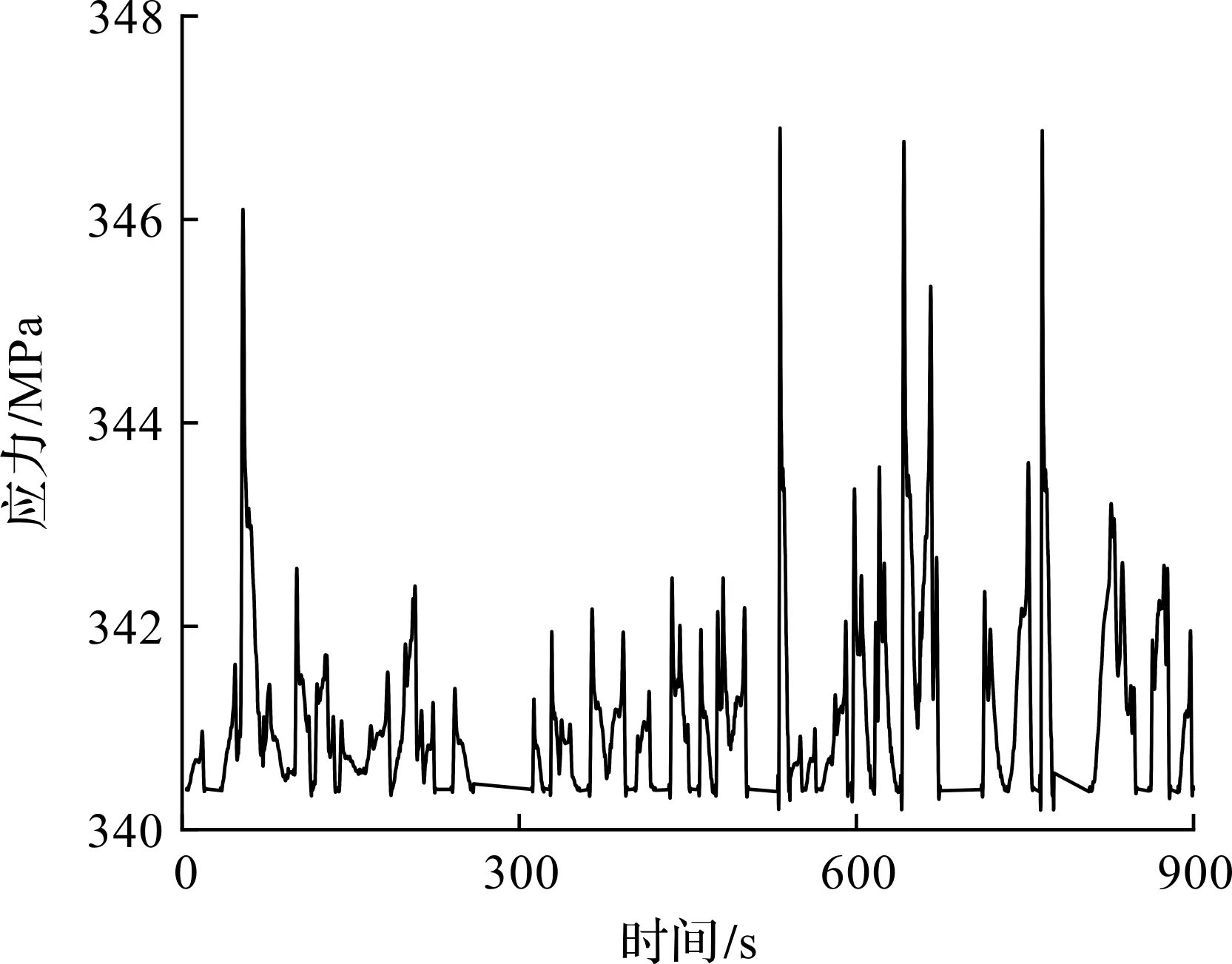
图6 吊杆H1时间应力曲线Fig.6 Time and stress curve of side span H1
该桥日均通过车辆接近60 000辆,程序运算较为繁琐,为了提高计算效率,采取以下3种措施:将每辆n轴车辆简化为在其轴位置处的n个集中力,并应用于车道的中心线;设置车辆总重阈值(在本研究中为30 kN)以忽略轻型车辆的载荷[10],因为有阈值和无阈值时疲劳损伤之间的差异非常小;在应力计算过程中设置适当的时间步长(在本研究中为0.1 s)。
3.2 应力计算的时间步长
时间步长是张力计算中的一个关键问题。如果时间步长过大,可能无法捕捉到张拉应力的峰值;时间步长太短可能会导致不必要的计算工作量。本节将研究不同时间计算步长(即0.1,0.2,0.5,1.0,2.0 s)的影响。同样,以2020年6月1日为例,某辆4轴货车通过桥面系吊杆H1的张拉应力历程如图7所示。由图7可知:除2.0 s以外,时间步长为0.1,0.2、0.5,1.0 s的时间历史的峰值几乎相同,都可以精确地捕捉到张力峰值。为了尽可能降低提取应力循环产生的疲劳损伤误差,本研究将时间步长设置为0.1 s。

图7 不同计算步长下的H1时间拉力曲线Fig.7 Hanger 1 time tension curve under differentcalculation steps
3.3 吊杆疲劳损伤的计算
因为影响线计算的张拉应力没有考虑车辆荷载动态效应产生的影响,所以计算得出的张应力应考虑乘以动态放大系数,以更贴近真实值。我国桥梁设计规范将动力放大系数定义为桥梁基础频率的函数,当桥基频率小于1.5 Hz时,动态放大系数可取为1.05。美国州公路及运输协会载荷与阻力系数设计(AASHTO LRFD)[11]提出:在疲劳极限状态下,除桥面接缝外所有部件的动态载荷容限(冲击系数)为0.15。马麟等[12]采用车桥耦合振动分析方法研究了某大跨度拱桥的动力放大系数,该桥主跨1 385 m,基频为0.086 8 Hz。结果表明:与中国桥梁设计规范相比,采用AASHTO LRFD规范的规定进行取值更加合理。在此基础上,将疲劳分析的动态放大系数保守设置为1.15。
将吊杆的拉应力σ定义为
(2)
式中:Td为恒载引起的吊杆张力;Tv为车辆荷载引起的张力;F为动态放大系数;A为吊杆的横截面积。
将时间步长设置为0.1 s,在吊杆的时间应力曲线中波峰和波谷数量较多,为了获取有效波峰和波谷,用雨流计数算法[13]处理张应力σ的应力历程,所得结果为吊杆的应力均值、幅值和循环数的关系图(图8)。利用提取的应力循环关系,使用Miner线性累积损伤理论[14]计算拱桥吊杆的疲劳损伤,即
(3)
式中:ni为当应力幅为Si时的循环数;Ni为当应力幅为Si时的疲劳寿命;D为疲劳损伤。
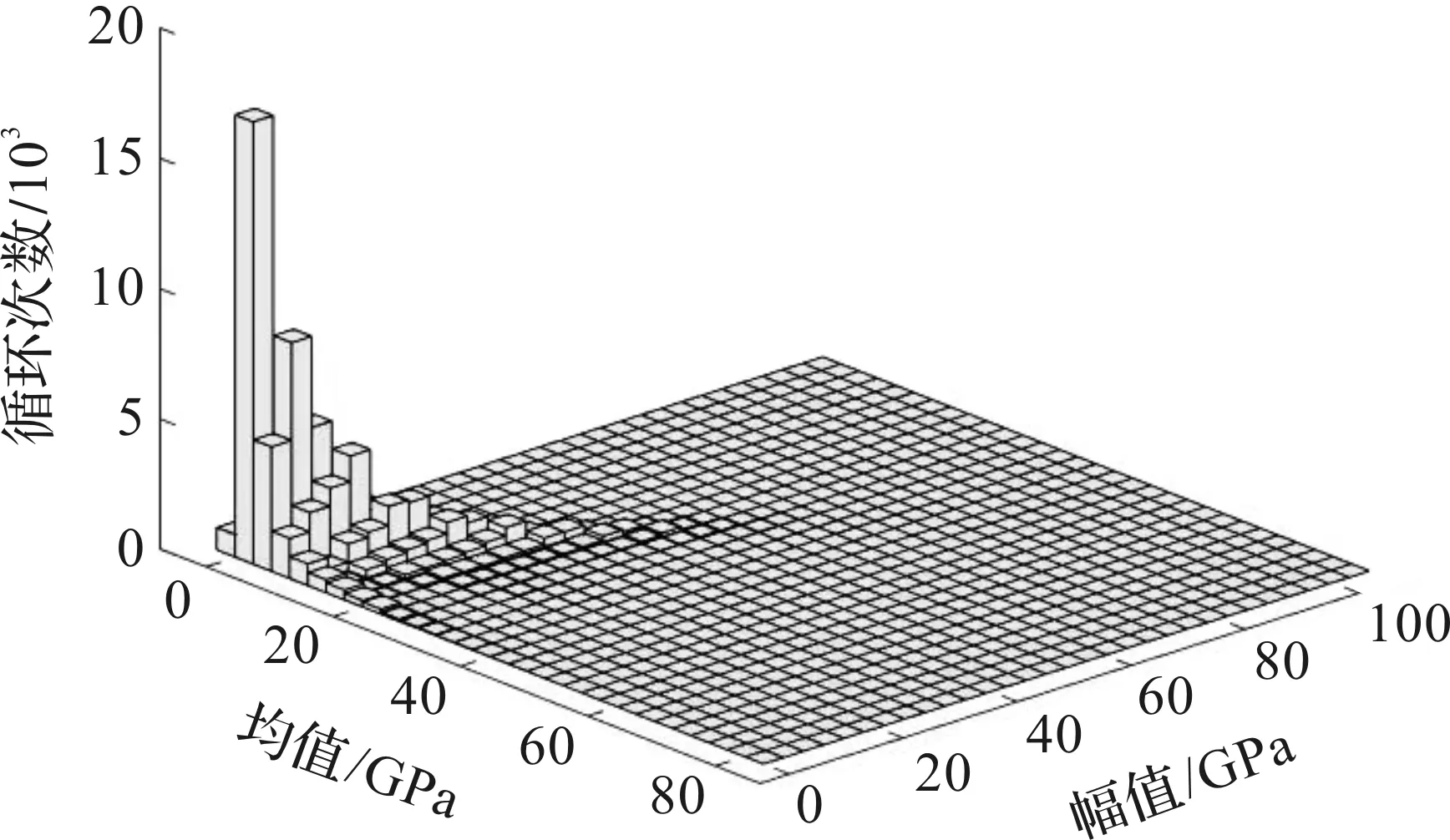
图8 2020年6月1日吊杆H1雨流计数图Fig.8 Rain-flow count of hanger 1 on 1 June 2020
该桥吊杆为平行钢丝索体系,均为121Φ7 mm。根据曾勇等[15-16]的研究,吊杆的S—N曲线近似为
logN=13.95-1.5logS
(4)
以往的研究表明吊杆的疲劳寿命是平均应力水平和应力幅的函数[17]。因此,将应力幅Sm修正为
(5)
式中:σm,σu分别为平均应力和极限抗拉强度。因此式(4)中的应力幅S应替换为Sm。
最终计算所得吊杆的日疲劳损伤值如图9所示。从桥梁中跨到两边桥头,吊杆的疲劳值呈下降趋势。中跨吊杆的疲劳值约为边跨的6倍。
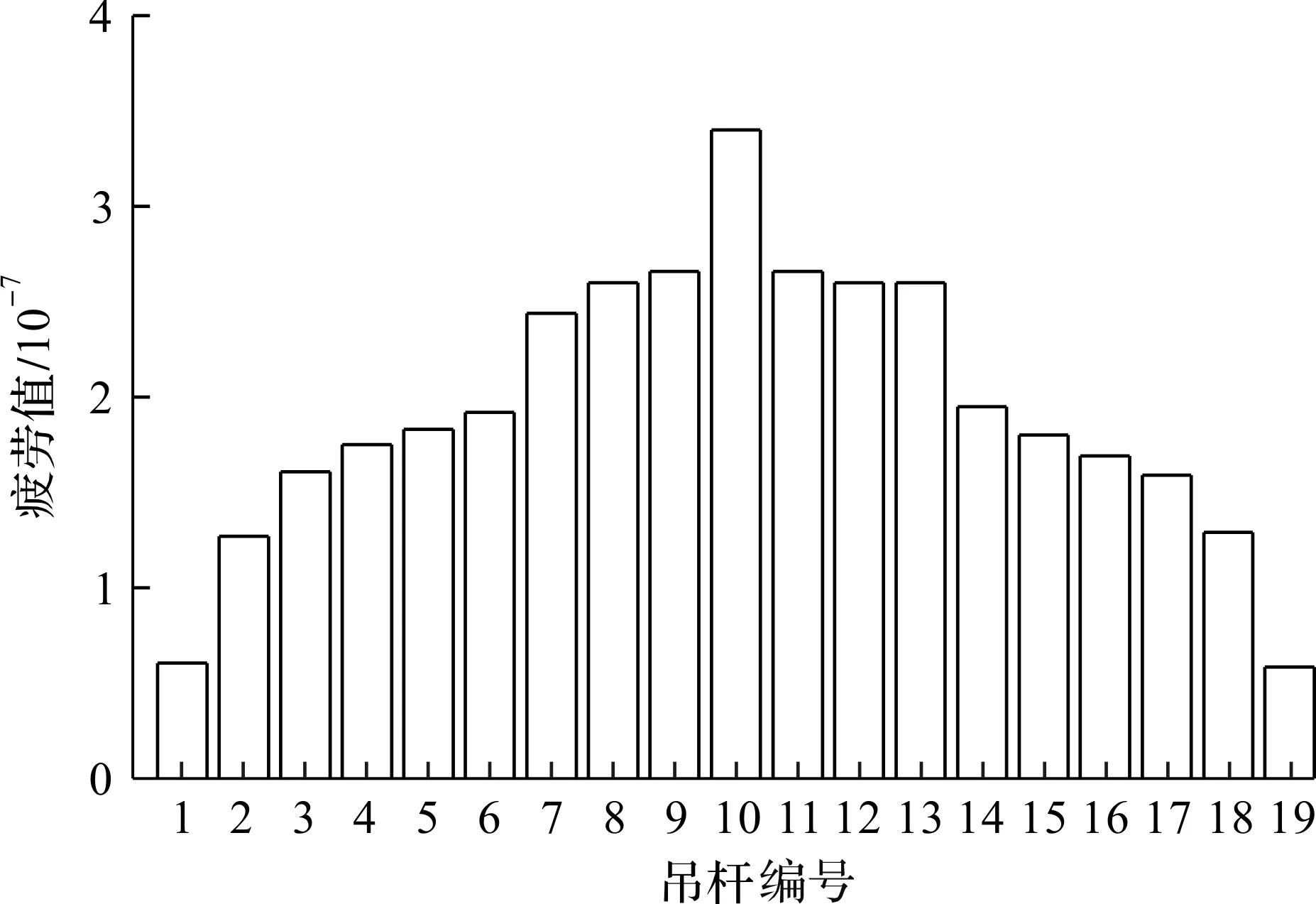
图9 2020年6月1日吊杆日疲劳损伤值Fig.9 Daily fatigue damage value of the hangerson 1 June 2020
3.4 疲劳损伤评估和寿命预测
笔者收集了九堡大桥2020年6—8月的动态称重数据用于计算吊杆的疲劳损伤。吊杆的日平均疲劳损伤值可表示为
(6)
式中:Di为第i天的疲劳损伤值;l为月份的天数。吊杆6—8月的日平均疲劳损伤如图10所示。
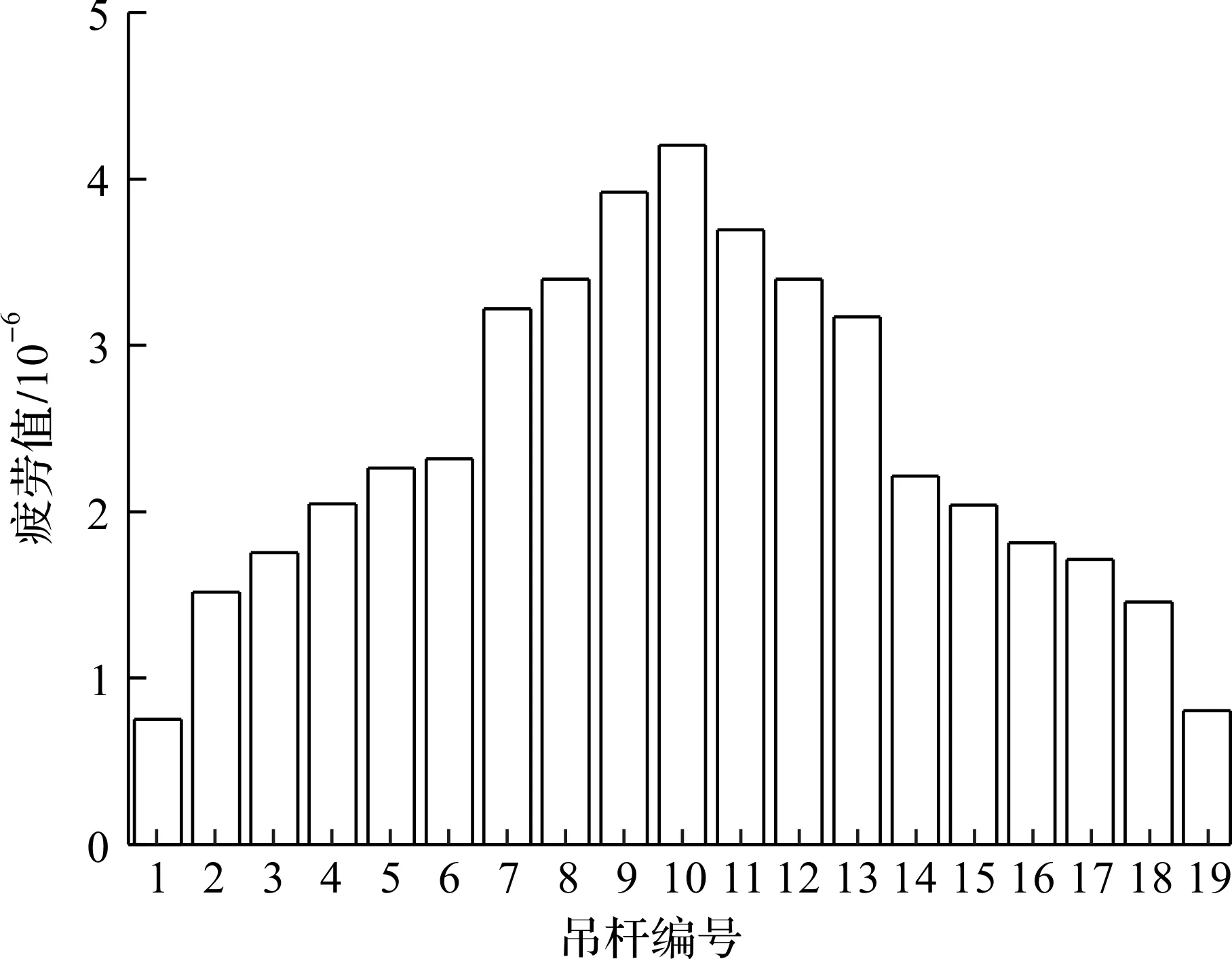
图10 2020年6—8月吊杆日均疲劳损伤值Fig.10 Average daily fatigue damage value of hangerfrom June to August 2020
假设通过该桥的车辆数目与车辆载重在短期内没有大幅度地增加或降低,可以将2020年6—8月的吊杆日疲劳值作为吊杆未来几年内的吊杆日疲劳值进行计算,那么吊杆的疲劳寿命T可表示为
(7)
2020年6—8月日平均疲劳损伤得出的疲劳寿命如图11所示。由图11可知:从桥两端到桥跨中,吊杆的疲劳寿命呈现下降趋势。以2020年6—8月的日均疲劳值进行预测时,吊杆的疲劳寿命均超过500 a,最短为651 a。跨中吊杆疲劳寿命最低,在役桥梁吊杆管理养护、更换时应优先考虑跨中的吊杆。2020年6—8月动态称重数据与疲劳寿命比较如表2所示。由表2可知:在2020年6—8月期间,当日均通过车辆数量、平均车重均以低于20%的幅度增长时,吊杆疲劳损伤值呈现数量级增长,2020年6—7月的预测疲劳寿命值相差接近2倍,2020年7—8月的预测疲劳寿命值相差接近9倍,2020年8月预测数据显示中跨吊杆的疲劳寿命仅为246 a。从桥两端到桥跨中,吊杆疲劳寿命的减小速度是逐渐增大的,交通荷载的增长可以显著加速疲劳损伤的发展,吊杆疲劳性能的研究不应根据经验作判断,而应基于长期的现场实测车辆载荷。

图11 2020年6—8月日平均疲劳损伤得出的疲劳寿命Fig.11 Fatigue life derived from average fatigue damagefrom June to August 2020

表2 2020年6—8月动态称重数据与疲劳寿命比较
Petrini等[6]用概率的方法模拟了一座大跨度悬索桥未来一年里所受到的风荷载与列车荷载,对吊杆的疲劳损伤进行了估算,在风荷载或者列车荷载的单独作用下,桥塔附近吊杆的疲劳寿命均超过1 000 a。汪小超等[8]采用了蒙特卡洛法考虑车辆荷载的横向分布,对大跨度悬索桥在车流荷载作用下吊杆的疲劳损伤进行了评估。结果显示:当仅仅采用1个月的车流数据进行疲劳寿命预测时,吊杆的疲劳寿命均超过5 000 a;当采用1月与8月的数据进行疲劳预测时,两者所得结果相差超过25倍。对吊杆疲劳寿命进行评估分析时,仅采用单日或者单月的数据可能得到差距很大的预测值,采用尽可能大的时间跨度下的数据会得到更合理的预测结果。
3.5 疲劳损伤评估预测分析
影响吊杆疲劳寿命的因素很多,其中包括车辆荷载、环境侵蚀、桥梁初始设计缺陷、动力效应、风荷载和温度荷载等。笔者方法在评估在役吊杆时也存有一些弊端:1) 在进行疲劳分析时只考虑了单一的影响因素;2) 在使用雨流计算法进行分析时,在众多的峰谷里可能没有准确地捕捉到对疲劳寿命影响较大的波峰和波谷;3) 针对动态效应放大系数应先根据不同工程作不同分析,再得出相应的值,而本研究只是取了规范里的值。吊杆疲劳寿命预测是十分具有挑战性的研究,在实际工程应用中桥梁所承受的外荷载,即车辆等外激励荷载不仅难以实时地精确测试[18],而且很难对多个外部荷载作用下的随机结构响应以及在桥梁长期使用过程中外部荷载可能发生的变化进行表征和建模。在未来的研究中,应该致力于研究多个影响因素情况下疲劳损伤评估和寿命预测。
4 结 论
笔者提出了一个研究组合结构拱桥吊杆在现场实测车辆荷载作用下疲劳性能的框架。基于实测动态称重系统收集的实时车辆数据,以九堡大桥为研究对象,对吊杆疲劳性能进行了研究,得出如下结论:1) 从桥两端到桥跨中吊杆的疲劳寿命呈现下降趋势,在役桥梁吊杆管理养护、更换时应优先考虑中跨的吊杆;2) 吊杆疲劳寿命的减小速度是逐渐增大的,车辆数量、车辆总重小幅度的增加会造成吊杆疲劳损伤值数量级增长,因此在实际工程中针对吊杆疲劳性能的研究不应根据经验作判断,而应基于长期的现场实测车辆载荷;3) 在对吊杆疲劳寿命进行评估分析时,仅采用单日或者单月的数据可能得到差距很大的预测值,采用尽可能大的时间跨度下的数据会得到更合理的预测结果。
