基于经验模态分解的RV减速器运动参数降噪研究

宋 雷， 游东东， 郑振兴， 周玉山， 陈龙崇

(1. 广东技术师范大学 机电学院，广州 510635； 2. 华南理工大学 机械与汽车工程学院，广州 510640； 3. 广州汽车集团股份有限公司 汽车工程研究院，广州 510640)

RV(rotate vector)减速器是在摆线针轮传动基础上发展起来的一种二级减速传动装置。与经典的行星传动形式相比，该减速器采用共享曲柄轴和中心圆盘支撑的结构形式组成封闭式行星传动，具有传动比大、体积小、质量轻、承载能力强、刚度大、运动精度高、传动效率高、回差小、寿命长、传动平稳等优点，近年来在机器人等精密传动领域得到了广泛的应用[1-3]。

传动精度是传动装置核心技术问题之一，日本的日高照晃等[4-5]、韩国的Kim等[6]、我国的杨玉虎等[7-8]国内外一大批知名学者针对RV减速器传动精度的建模、影响因素等进行了研究，相关成果对设计、制造产生了有效的指导作用。目前的研究主要关注零部件制造精度对RV减速器工作性能的影响，而在实际工程应用中，测控系统对整机运动精度的影响更加显著，单纯依靠提高制造精度的方式改善传动精度成本较高，且效果不明显，采用有效的信号处理算法，准确获取RV减速器的运动参数，可以为后续的精密控制与误差补偿提供可靠的数据。

经验模态分解(empirical mode decomposition, EMD) 算法是由Huang等[9-10]于1998年提出，该算法可以自适应的对非平稳、非线性信号进行分解，已经广泛应用于信号降噪、特征提取、智能识别等领域，获得了广泛的认可。EMD算法可以按照信号的特性完备的分解为多个不同的固有模态函数(intrinsic mode function,IMF)，这为有效进行降噪处理提供了良好的基础。目前使用EMD进行降噪处理主要有两种策略，一种是基于阈值的策略，即EMD-T(EMD Thresholding)；另外一种是基于信号重构的策略,即EMD-PR(EMD part reconstruction)。EMD-T是受小波降噪处理启发，根据设定的阈值对EMD分解得到的IMF分别进行处理，实现滤除噪声的功能。为了提高降噪效果，希腊的Kopsinis等[11]以IMF相邻过零点之间的间隔为对象进行阈值处理，提出了EMD-IT(EMD interval thresholding)滤波策略，我国的余腾等[12]将EMD与小波阈值滤波结合起来应用在桥梁监测信号的降噪中，取得了较好的效果。基于EMD的信号重构降噪首先对信号成分进行有效区分，并通过重构去除噪声成分，保留信息成分。在EMD-PR中，如何对IMF进行有效区分是算法的关键，法国的Boudraa等[13]针对这一问题构造了连续均方误差(consecutive mean square error, CMSE)指标，并在文献[14-15]中得到应用。此外Komaty等[16]还根据相似性度量提出了基于l 2范数的区分准则。

目前基于EMD的信号降噪研究中，主要是采用单一指标，将信号分解为噪声成分和有效成分，但由于相关指标的局限性，造成信号成分的划分存在一定差异，影响了信号降噪的准确性。本文采用EMD算法对RV减速器运动参数进行降噪处理，将CMSE和l 2范数相结合，把IMF区分为噪声占主要成分的IMF(简称为噪声IMF)，信息占主要成分的IMF(简称为信息IMF)，以及噪声与信息成分相当的IMF(简称为混合IMF)，并进行重构降噪，有效抑制运动参数的噪声干扰，显著提高了信号的信噪比。

1 基于EMD-PR的降噪方法

1.1 EMD算法

EMD算法认为不同的信号成分的波动相互叠加，每个波动都表征了信号的一个特征尺度，而极值点间的时间间隔作为筛选信号波动的时间尺度，根据信号本身的特征自适应的提取出信号中固有的波动特征，将原始的多分量信号分解为多个单分量信号的和。在EMD算法中，分解得到的单分量波动特征叫做固有模态函数，其应符合两个条件：

(1) 信号的极值点数量和过零点数量必须相等或最多相差一个。

(2) 在信号的任一时间点处， 由局部极大值点构成的上包络线和由局部极小值点确定的下包络线的均值为0，即信号关于时间轴局部对称。

EMD算法通过对信号进行自适应的筛选，将原始信号x(t)分解为一系列IMF分量FIM,i(t)与残余信号r(t)的和，为方便表述，将残余信号r(t)也看作IMF，即

(1)

1.2 基于CMSE的IMF区分准则

原始信号x(t)中包含了多种成分的噪声信号，在分解过程中EMD算法具有从高频到低频依次进行分解的特性，一般来讲，低阶的IMF频率较高，噪声信号占据主要成分，高阶IMF频率较低，真实信号占据主要成分。基于这一推断，通过对不同阶数的IMF进行筛选与处理，并进行信号重构，就可以实现对噪声信号的滤除，这也是EMD-PR滤波的基本思路。

对于不同阶的IMF，存在某一阶数M1，在该阶数之前的IMF噪声占据主要成分，在该阶数之后的IMF中真实信号占据主要成分。对于噪声IMF，当阶数由低向高递增过程中，噪声信号的能量逐渐降低，而对于信息IMF，当阶数由低向高递增过程中，信息信号的能量逐渐增加，因此可以将IMF能量作为区分噪声IMF和信息IMF的指标。Boudraa等依据此分析提出了ECMS

(2)

其中

(3)

根据上面的分析，噪声与信息IMF的分界点为

(4)

对于实际信号，CMSE通常不是单调函数，而是存在一定的波动，如果直接采用式(4)对IMF进行划分，会造成划分不准确。越低阶的IMF噪声成分越明显，因此可以将M1定义为CMSE的第一个极小值出现的位置

(5)

1.3 基于l 2范数的信号相似性度量

采用式(5)虽然可以选择出噪声IMF，但却忽略了混合IMF，有必要将混合IMF与信息IMF做区分，以提高降噪的准确度。两个对象接近程度可以用距离进行度量，在EMD分解中，信息IMF可以通过度量IMF与原始信号的相似程度进行选取。信号是多种因素相互作用的结果，特别是随机因素难以忽视，直接对时域信号进行度量受随机因素影响过大，难以反映两个信号实际的相似程度，以信号的数据概率分布进行相似性度量，可以更加真实的度量两个信号之间的相似程度。l 2范数是较为常用的一种距离度量方式，也被应用于信号相似性的度量中。两个点集的概率密度函数分别为P和Q，则两者之间的l 2范数为

(6)

对于信号S1(t)和S2(t)，求得信号的概率分布密度函数分别为FPD,S1(t)和FPD,S2(t)，因此基于距离L的两个信号相似性可定义为

(7)

在Komaty等的研究中，是按照式(8)对IMF进行分割，选取出信息IMF。本文通过式(5)可以选取出噪声IMF，直接采用式(8)计算得到的M2会与M1过于接近，难以有效区分噪声IMF和信息IMF，甚至产生重叠，一般来讲，噪声IMF的阶数较低，信息IMF阶数较高，在采用式(5)确定M1的条件下，采用图1所示准则选取M2。

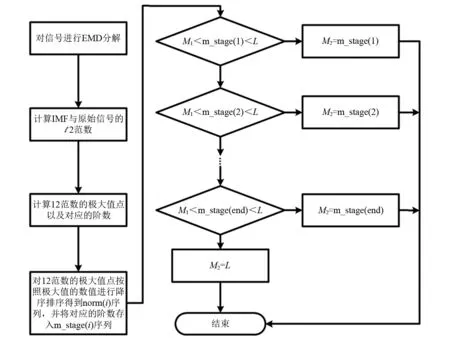
图1 M2阶数选取准则Fig.1 The criterion of M2 selection

(8)

1.4 降噪算法框架

通过CMSE和l 2范数可以将EMD分解得到的IMF划分为噪声IMF、混合IMF、信息IMF的三部分，在降噪处理中，对噪声IMF采用直接去除的方式；对混合IMF在经过降噪之后可用于信号的重构；而对于信息IMF则可直接用于信号的重构。Kalman滤波是一种十分有效的实时信号处理方法，可以有效滤除信号的白噪声。信号通过EMD分解后，IMF近似为线性、平稳信号，而对于混合IMF可以采用Kalman滤波进行降噪，提高信号的准确性。为了抑制EMD分解过程中的模态混叠，在分解过程中使用EEMD分解算法；为了抑制端点效应，采用镜像延拓的方法进行处理。本文的噪声处理算法框架如图2所示，主要步骤为：

图2 降噪算法框架Fig.2 The framework of denoising algorithm

步骤1对信号进行EEMD分解，得到IMF。

步骤2计算IMF的CMSE，根据式(4)确定M1。

步骤3计算IMF与原始信号之间的l 2范数，确定M2。

步骤4对M1+1阶到M2阶IMF进行Kalman滤波。

步骤5将Kalman滤波后的M1+1阶到M2阶IMF，以及M2+1阶-L阶以及余项进行求和，得到重构信号。

该算法可以将信号完备的分解为3个部分，采用不同策略对这三部分信号进行处理，通过重构实现对信号的降噪，可以较好的适应非线性信号的处理。

2 RV减速器试验测试与运动参数降噪

2.1 RV减速器测试试验

以RV40E作为典型的减速器型号，采用减速器专用测试平台对RV减速器进行运行参数测试试验，如图3所示。伺服电机与RV减速器的输入轴之间安装了转矩转速传感器，检测RV减速器输入端的运行参数，RV减速器输出端与负载之间也安装了转矩转速传感器，测量RV减速器输出端的运行参数，输入端和输出端的传感器分别为瑞士Kistler公司的4502A50RA和4503A1KLA 100000传感器。

1. 伺服电机； 2. 输入端转速转矩传感器； 3. RV减速器； 4. 输出端转速转矩传感器； 5. 摩擦轴负载。图3 精密减速器测试平台Fig.3 Measurement platform for precise reducer

转速与转矩是减速器运转过程中最直接的两个参数，也是运行过程中需要进行实时控制的两个核心参数，因此将这两个参数作为研究对象，选取输入转速分别为1 000 r/min，2 000 r/min，3 000 r/min 3个条件进行测试，测试过程中采样频率为1 000 Hz，测得RV减速器输入和输出端转速和转矩如图4～图6所示。

图4 输入为1 000 r/min条件下RV减速器运行参数Fig.4 RV reducer operation parameters under 1 000 r/min

图5 输入为2 000 r/min条件下RV减速器运行参数Fig.5 RV reducer operation parameters under 2 000 r/min

图6 输入为3 000 r/min条件下RV减速器运行参数Fig.6 RV reducer operation parameters under 3 000 r/min

2.2 RV减速器运行参数的降噪处理

从测试数据中可以看出，转速数据噪声较小，数据较为稳定，可以不再进行降噪处理，而转矩数据具有较为明显的噪声信号，如果直接将这些原始数据应用于控制，将对整个系统造成控制误差和额外的冲击，甚至会影响系统的稳定性。

对于输入端的转矩主要受伺服电机控制，从测试获得数据看，输入端转矩信号的噪声主要以白噪声为主，可以推断造成噪声的主要来源为传感器内部电路，而输出端转矩则具有明显的周期性波动，这与减速器的传动特性有直接关系，此外测试过程中产生的噪声干扰与这种周期性的波动相叠加，造成转矩信号噪声干扰较为明显，有必要对转矩信号进行降噪处理。选取3 000 r/min条件下的转矩信号作为典型信号，应用本文提出的降噪方法进行降噪处理。对输入端和输出端的转矩分别进行EMD分解，得到IMF如图7所示。

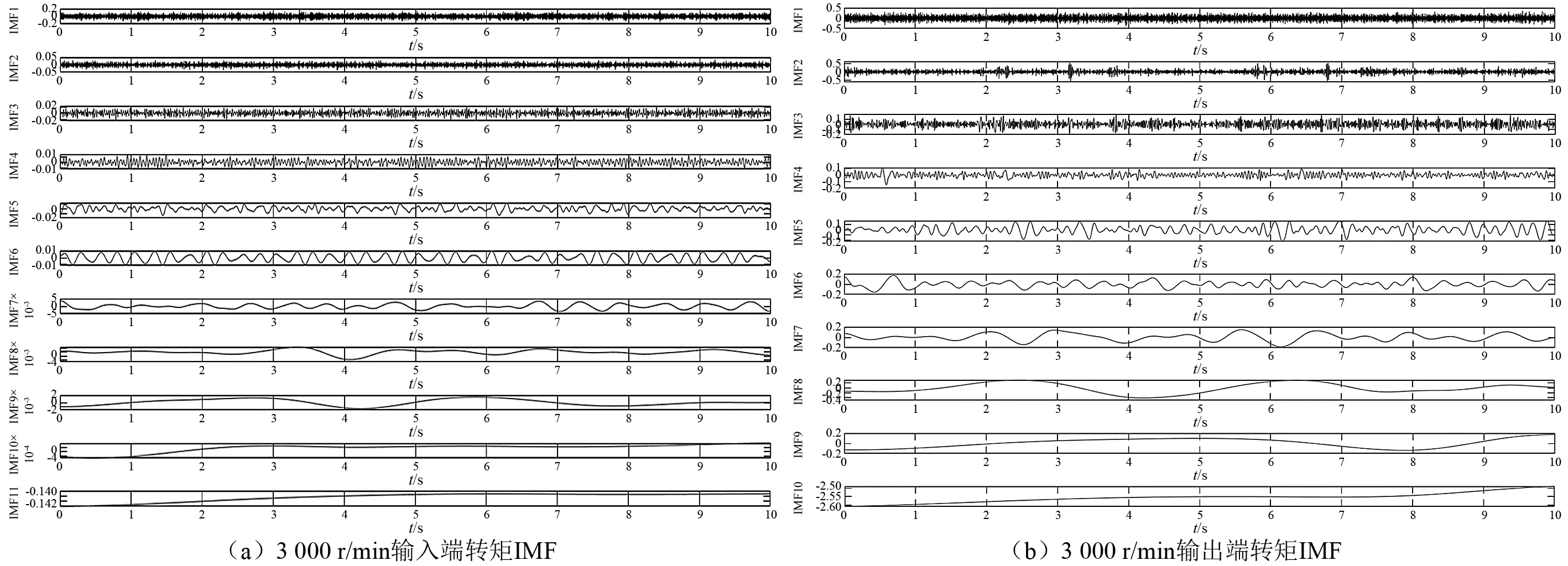
图7 RV减速器转矩信号IMFFig.7 IMFs of RV reducer torque

根据EMD分解得到的IMF，计算得到CMSE，如图8所示，IMF与原始信号之间的l 2范数计算结果如图9所示。根据式(5)和图1所示准则选取输入端转矩IMF的M1和M2阶数分别为4和10，输出端转矩IMF的M1和M2阶数分别为4和9。

图8 转矩IMF的CMSEFig.8 CMSE of torque IMFs

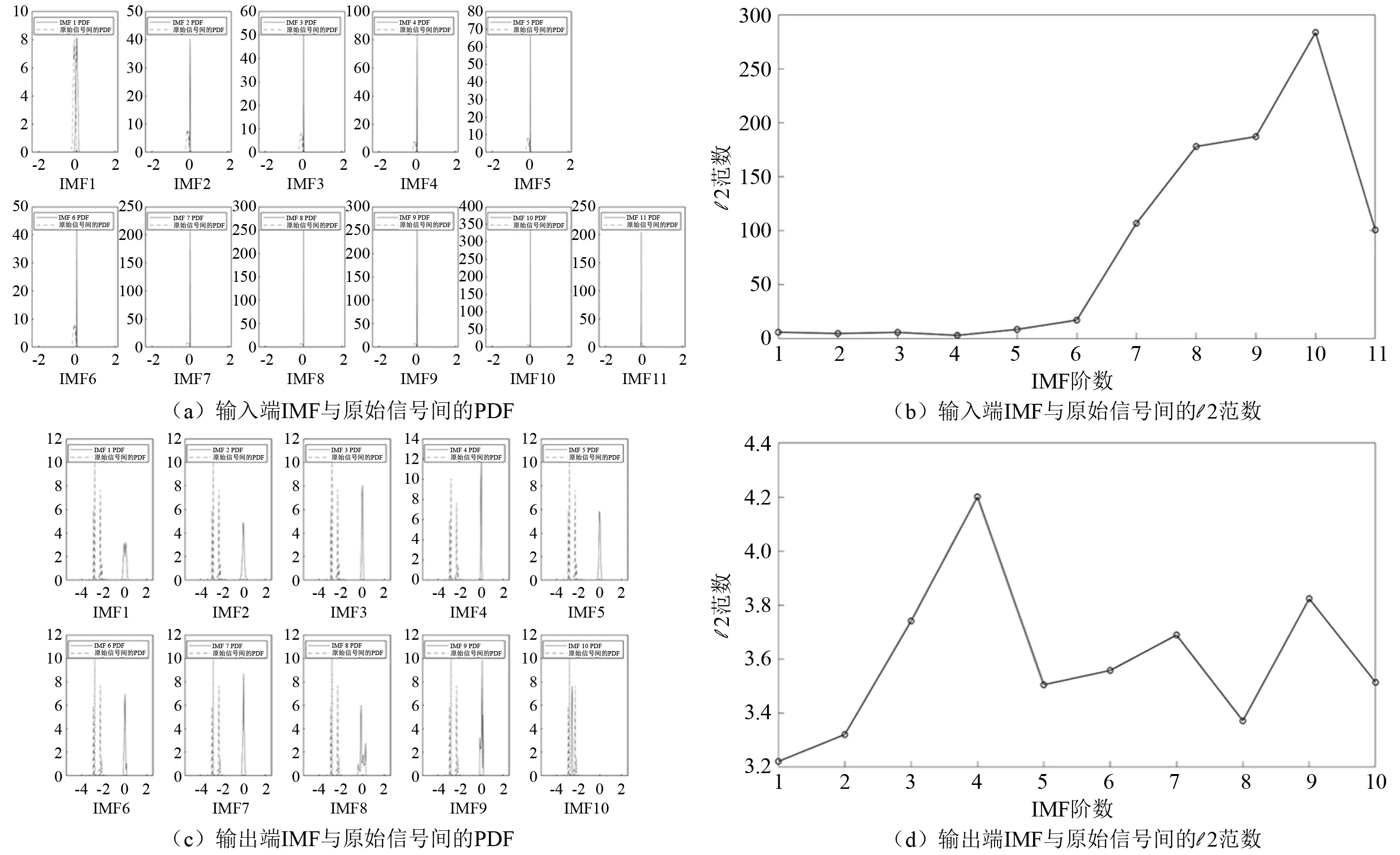
图9 转矩IMF与原始信号间的l 2范数Fig.9 l 2-norm between IMFs of torque and original signal

M1+1到M2阶IMF包含有一定比例的噪声成分，为了提高信号准确程度，对M1+1到M2阶IMF进行Kalman滤波，结果如图10所示。在信号重构中，直接将1～M1阶噪声IMF忽略，M1+1阶、-M2阶含有一定成分的噪声，可以在滤除噪声后用于信号重构，M2+1阶之后的信号为信息IMF，可以直接用于重构。重构后的信号入图11所示。

图10 IMF进行Kalman滤波后的结果Fig.10 Kalman filtering results of IMFs

图11 RV减速器转矩信号重构Fig.11 The reconstruction of RV reducer torque signal

应用该方法对1 000 r/min和2 000 r/min条件下的输入端和输出端转矩信号进行降噪处理，结果如图12所示。

血常规检验是可以对早期病变进行发现的一种有效的检测方式,对骨髓造血、血循环等等问题可以尽早的发现 [3]。现在临床中血液检测的技术日趋成熟,检测的工作变得完善,检测的精度也有了很大的提升。但是,我国使用的三级分类是以白细胞大小作为基准,对嗜酸、幼稚细胞及粒性细胞进行鉴别,而对中性粒细胞、变异性淋巴细胞的鉴别效果不是十分理想。部分仪器会将小型粒细胞判断为中间细胞,把大淋巴细胞当成粒细胞,因此而引发了检验的结果偏差。因此临床中对于血常规检测的重视度必须足够高,尤其是血涂片分析,能够对血细胞指标进行观察,获得的结论能够给临床治疗提供依据,为患者进行复查。

图12 1 000 r/min和2 000 r/min转矩信号降噪结果Fig.12 The results of denoised torque signals at 1 000 r/min and 2 000 r/min

2.3 结果分析

在3个转速条件下，无论是输入端还是输出端转矩信号噪声成分较为显著，随着转速的升高，测得的转矩信号中噪声成分有所增加，但总体而言，噪声对转矩信号的影响较为明显，对真实信号形成了较为严重的干扰。除去噪声的影响，输入端的转矩主要呈现定值特征，这说明输入端的转矩主要受驱动电机控制，输入端转矩信号的噪声主要来自传感器，从噪声信号的影响程度来看，噪声对真值的影响较大，如果直接采用传感器数据，会带来较大的误差。

RV减速器输出端的转矩呈现明显的谐波波动，这与减速器的固有特性有直接关系，与输入端转矩测试数据相类似，输出端转矩信号也具有较为明显的噪声成分，造成输出端噪声的主要原因除了传感器产生的噪声之外，机械结构的振动也是不可忽略的因素之一。

在对信号相似性进行度量的过程中，两个信号概率分布的均值以及概率的峰值都对信号的相似性产生直接的影响，均值的差异表示两个信号基本值的不同，而概率峰值的差异则表示了信号形态的不同。采用l 2范数进行度量并没有对这两种差异进行有效的区分。从l 2范数的几何意义上来看，l 2范数越小，说明两个信号的距离越短，也就是两者越相似；从l 2范数度量结果上看，低阶的IMF主要为噪声成分，但其l 2范数却小于高阶IMF，造成这种现象的主要原因在于l 2范数在度量过程中把信号均值的差异和形态的差异都包括进来了，无法直接表示信号的近似程度。因此在利用l 2范数对信号相似性进行分析时，如果直接根据l 2范数对信号相似性度量会造成不准确的结果，在比较过程中应将低阶IMF和高阶IMF分别进行对比分析。从l 2范数分布情况上看，每一组IMF的最后一阶的l 2范数都是下降的，这说明最后一阶IMF与原始信号的相似度变高，这符合 EMD的分解特性。从CMSE对IMF度量中可以看到，低阶的IMF能量非常低，能量主要集中在最后一阶IMF，这说明EMD分解得到的最后一阶IMF近似于信号中的直流分量，反映信号的稳态作用。除去最后一阶IMF，其余CMSE大致位于同一数量级，且有多个极值点，因此采用第一极小值点对IMF进行区分并不能将噪声成分完全去除，有必要采用与其他的区分指标相配合，更加完整的去除噪声成分。将CMSE主要用于低阶IMF的区分，将l 2范数主要用于高阶IMF的区分。

对降噪前后的转矩信号计算信噪比，结果如表1所示，从表1可以看出，采用本文提出的基于EMD的降噪方法处理，转矩信号的信噪比得到明显的提高，这说明该方法可以抑制转矩信号中的噪声。从表1也可以发现，输入端转矩的信噪比要明显低于输出转矩，这说明输入端的转矩较小，其信号较容易受到传感器等外部因素的干扰，经过减速器之后，转矩明显增大，外部因素对其信号影响程度减弱，但转矩呈现明显的周期性波动，这主要是由减速器引起的，通过降噪处理之后，可以更加准确的提取出这种波动，为误差补偿提供可靠的依据。

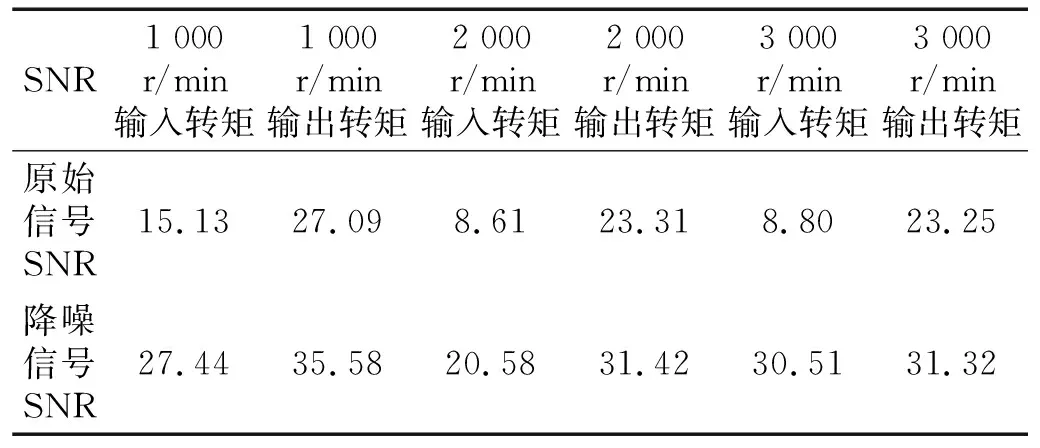
表1 降噪前后信号信噪比比较Tab.1 Signal SNR comparison between denoised and original

3 结 论

RV减速器是一种精密传动机构，现场采集到的运行参数具有较为明显的噪声成分，这成为影响控制精度主要因素，也大大影响了RV减速器的自身性能。本文基于EMD算法采用Part Reconstruction的策略对RV减速器的运行参数进行了降噪处理。

(1) 采用CMSE和基于概率的l 2范数将EMD分解得到的IMF区分为噪声为主要成分IMF、噪声与信息成分相混合的IMF、信息为主要成分IMF，并对选取准则进行了修正。

(3) 对RV减速器进行了试验测试，通过试验数据发现RV减速器的转速数据精度较高，噪声成分较少，可以直接用于控制，转矩数据无论是输入端还是输出端都具有明显的噪声成分，需要经过降噪处理才能用于后续的使用，采用本文提出的基于EMD-PR消噪方法对转矩信号进行了消噪处理，消噪的信号噪声成分得到有效的抑制，信号的平滑性得到明显的改善。