一种0°带束层结构全钢子午线轮胎模态分析方法
2022-09-30张维雁黄继文吴群华柴德龙
张维雁,黄继文,吴群华,柴德龙
(中策橡胶集团股份有限公司,浙江 杭州 310018)
模态分析研究的是系统动力学特性,这些特性独立于作用到系统上的外界激励和系统响应。动力学特性包括频率、阻尼和模态振型,可以通过有限元仿真得到,也可以通过试验由参数识别获得。模态分析是研究全钢子午线轮胎振动特性的重要手段,随着有限元分析技术的发展,其在降低轮胎研发成本和缩短研发周期上有相当大的优势[1-5]。
本工作以12R22.5全钢子午线轮胎为例,建立轮胎的振动模态有限元分析模型,结合振动模态试验测试结果,验证轮胎振动模态有限元分析方法的可行性及结果的有效性。
1 有限元分析
1.1 有限元模型的建立
首先用CAD软件画出材料分布图,去除花纹部分,通过Hypermesh软件进行网格划分及材料赋予,建立轮胎二维轴对称模型;轮胎花纹部分通过UG生成单节距实体花纹,再通过Hypermesh对其进行网格划分及材料赋予,然后旋转生成环形花纹,将去除花纹部分与花纹圈部分通过Abaqus中的接触功能耦合在一起。
关于材料与单元方面,橡胶采用大量CGAX4H和少量CGAX3H轴对称单元模拟,按弹性材料赋予弹性模量、泊松比和密度。将钢丝帘线看作加强筋结构,再利用Abaqus中的rebar功能来模拟,带束层、胎体和钢丝包布都尽可能按实际帘布厚度划分网格,其中加强筋用rebar layer定义,钢丝帘线用rebar定义。
目前Abaqus可以用隐式算法和显示算法来进行轮胎的模拟分析,考虑到本次模拟为静态模拟,采用隐式算法模拟分析轮胎装配、充气、加载等准静态过程的力学行为,可以得到较精确的计算结果。由于轮胎分析时存在复杂的材料非线性、几何非线性和接触非线性,因此隐式算法分析过程中需要大量的迭代过程,且常会出现迭代不收敛,无法完成计算情况,此时需要对网格进行合理划分,以达到最佳计算效果。
考虑到轮胎为3层带束层加两肩缠绕2层0°带束层的结构,为充分考虑0°带束层在轮胎实际充气下的伸张状态,从Abaqus提供的超弹性本构模型Polynomial,Ogden,Arruda-Boyce,Van der Waals和Marlow中选用Marlow模型,通过试验得到0°带束层钢丝帘线的应力、应变数据。
使用Marlow模型能更准确地模拟轮胎充气后的状态,轮胎外轮廓扫描与计算结果对比见图1,加载下轮胎实测与计算接地印痕对比见图2。
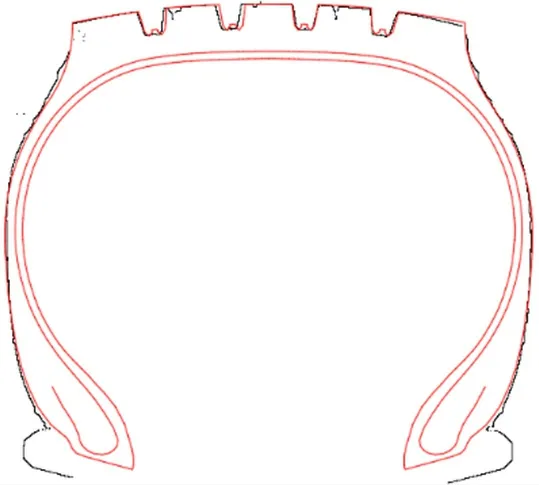
图1 充气轮胎外轮廓扫描与计算结果对比
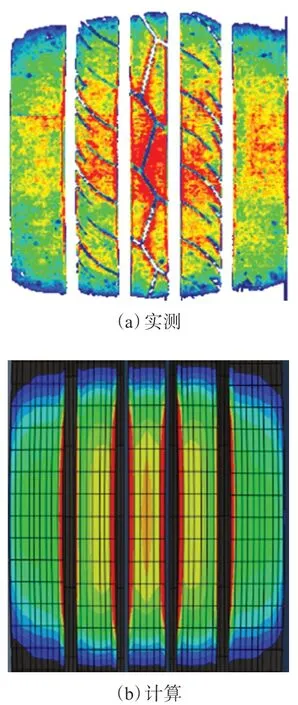
图2 实测与计算接地印痕对比
轮辋部分设定为完全固定约束,轮胎充气压力为930 kPa。轮胎的二维和三维有限元模型见图3,每个二维断面共划分了2 878个单元,圆周均分为90份进行分析,共将三维体划分为259 020个单元。
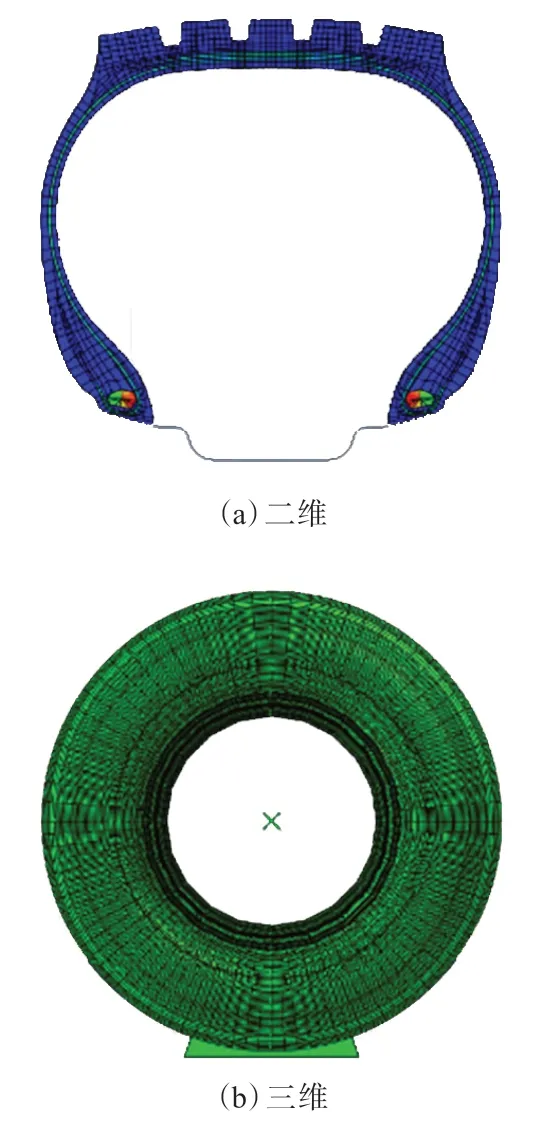
图3 轮胎有限元模型
1.2 理论方法
有限元模态分析实为按动力学响应系统的基本原理求解结构特征值及特征向量,也就是模态分析中的固有振动频率以及振型。其动力学基本方程为
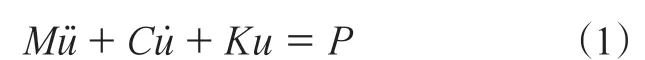
式中:M,C,K,P分别对应质量矩阵、阻尼矩阵、刚度矩阵以及各节点的负荷向量;,˙和u分别是系统各节点处的加速度列向量、速度列向量以及位移列向量。
若不考虑阻尼对结构振动的影响,则式(1)可简化为

若在此基础上,再假设各节点的负荷均为0,则式(2)可进一步简化为

式(3)即为系统自由振动时的动力学方程。
Abaqus具有3种用于模态计算的方法:subspace iteration,automatic multi-level substructuring(AMS)和Lanczos方法。Lanczos方法可在保证精度的前提下显著提高频率的计算效率,因此本研究采用Lanczos方法。
2 结果与讨论
表1和图4分别示出了轮胎在自由状态下1—6阶的径向振动固有频率及振型。
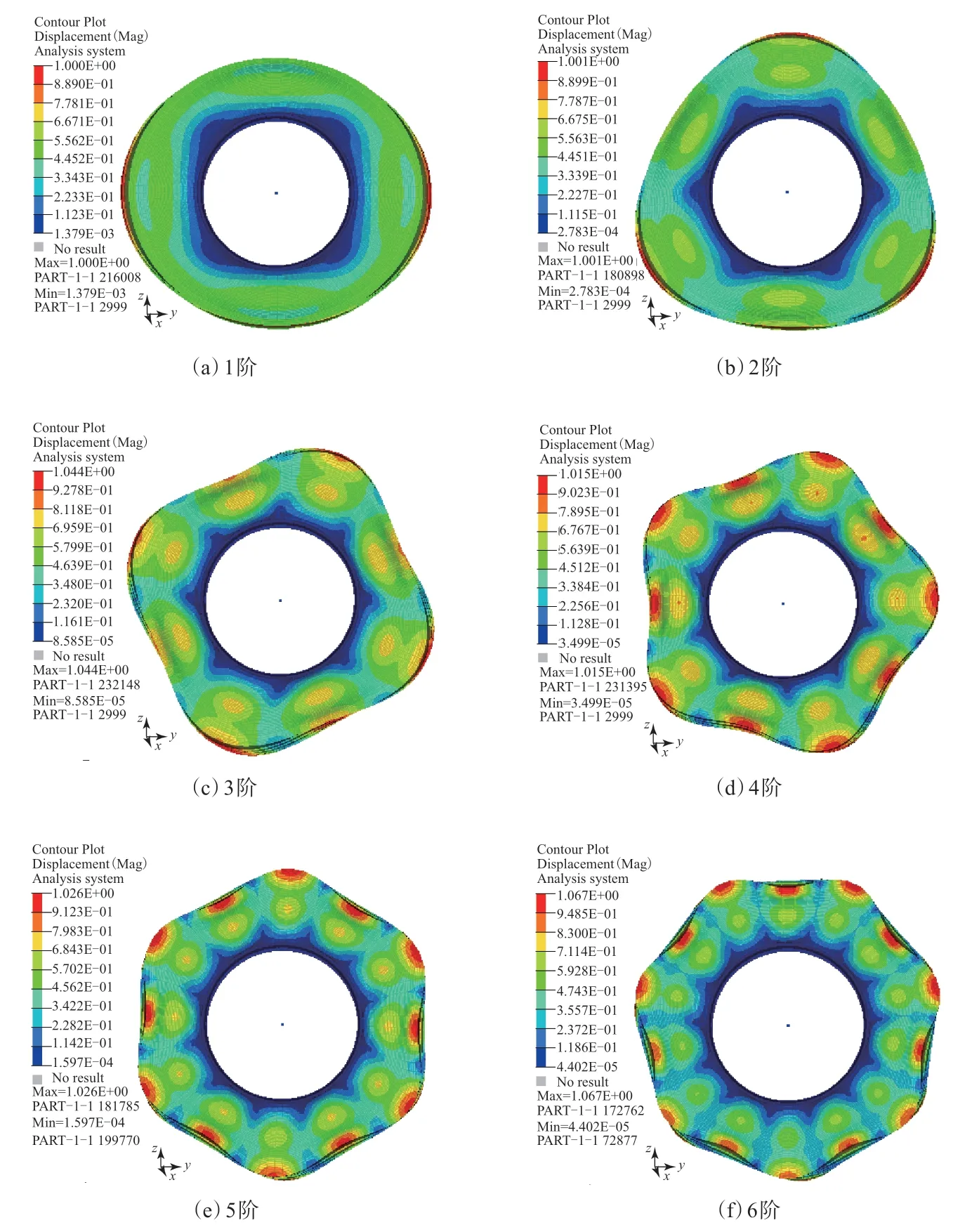
图4 轮胎径向振动1—6阶振型
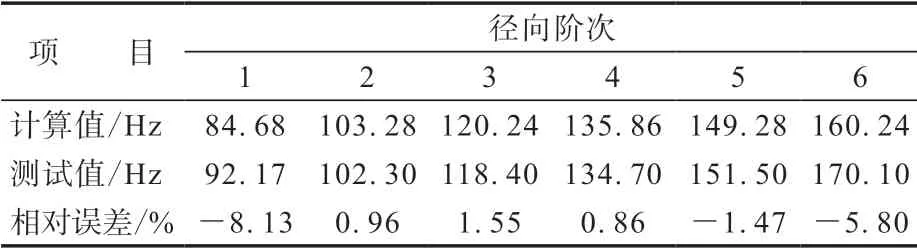
表1 轮胎1—6阶径向振动固有频率计算值与测试值比较
由表1可以看出,计算结果与测试结果的最大相对误差绝对值为8.13%,最小相对误差绝对值为0.96%,计算结果与测试结果有很好的一致性。造成部分误差较大的原因分析如下:(1)在材料设置中,将钢丝帘线作为薄膜rebar单元来分析,可能对准确性有一定的影响;(2)因全钢子午线轮胎质量较大,在测试过程中使用的吊绳可能未能处于完全自由状态。
图5 和6分别为轮胎周向振动1阶振型和轮胎横向振动1—4阶振型。
从图5和6可以看出:周向振动1阶振型中可发现轮胎在周向发生一定角度的旋转;随着阶次增加,轮胎横向振动左右扭动的部位增多。
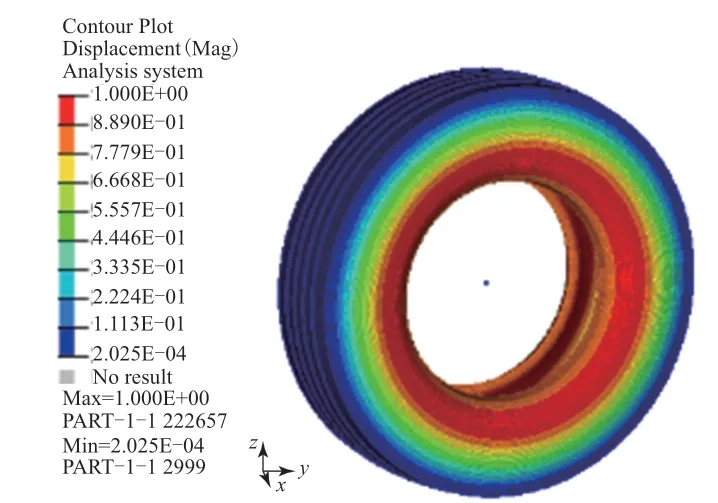
图5 轮胎周向振动1阶振型
3 结论
(1)通过CAD,UG,Hypermesh和Abaqus软件结合模拟计算复杂花纹全钢子午线轮胎的多阶固有频率及相应振型,针对含有0°带束层结构采用了Marlow模型,轮胎固有振动频率计算结果与测试结果有良好的一致性,说明此种建模方法的有效性。
(2)通过计算,得到轮胎的固有振动频率及径向、横向、周向的三维振型。
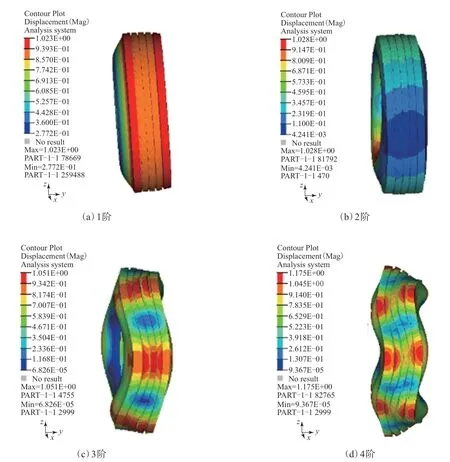
图6 轮胎横向振动1—4阶振型
(3)探讨了利用多款软件结合,更准确地分析轮胎基本振动的可行性,为研究滚动状态下的复杂花纹轮胎提供了一种方法。
