硬岩地层地铁暗挖车站施工过程力学分析
2022-09-30王柯黄成蒲万旭李为腾李永顺李洋
王柯, 黄成, 蒲万旭, 李为腾*, 李永顺, 李洋
(1.山东科技大学, 山东省土木工程防灾减灾重点实验室, 青岛 266590; 2.青岛市西海岸轨道交通有限公司, 青岛 266000; 3.中建八局轨道交通建设有限公司, 南京 210046)
随着地下轨道交通事业的发展,隧道工程建设数量日益增多且工况越加丰富、复杂[1-2]。地铁暗挖车站因其功能要求,一般属于浅埋、大跨隧道范畴。有关学者在此方面做了大量研究,蒋亮等[3]采用数值软件模拟台阶法施工,分析3种工况下浅埋隧道开挖引起的拱顶沉降和地表沉降的异同;徐剑波等[4]以沙子塘浅埋偏压隧道为依托,结合现场监测及数值模拟等技术手段,详细分析了典型监测断面围岩与支护结构相互作用关系;朱苦竹等[5]采用FLAC3D研究了分别使用双侧壁导坑法、交叉中隔墙法和三台阶七步法的浅埋软弱围岩大跨度隧道开挖过程,以确定最优的开挖工法;孔超等[6]以贵阳地铁某单拱大跨隧道为背景,通过开展模型试验,结合有限元极限分析法,对比分析不同工况施工过程中围岩变形规律以及拱盖结构极限承载能力。部分城市如青岛、大连、重庆等为典型的“上软下硬”地层,其地铁车站因此具有浅埋、硬岩、大跨的鲜明特点。郑世杰等[7]通过采用数值模拟和现场监测相结合的方法对青岛地区“上软下硬”复合地层双线平行隧道围岩变形特征和地层移动规律进行了研究;贾宝新[8]以大连地铁5号线地区盾构施工为背景,研究了在穿越上软下硬地层时盾构施工引起的地表沉降;Zhang等[9]通过数值分析推导了大断面隧道开挖围岩压力的计算公式,并将该公式应用于重庆某大断面地铁车站围岩压力的计算。
以上研究大多数是对浅埋隧道、大跨隧道、软岩隧道及硬岩隧道的沉降规律、围岩压力、施工工法等探究,但对同时兼具浅埋、硬岩、大跨特点的隧道施工过程力学分析少有人研究。现以青岛地铁暗挖车站浅埋硬岩大跨隧道为工程背景,在现场监测基础上采用三维数值模拟,研究浅埋硬岩大跨隧道施工过程力学特征,以期为类似工程设计提供依据。
1 工程背景
青岛地铁6号线海港路站为暗挖岛式车站,状况如图1所示。从图1(b)可知,地层从上至下依次为素填土层、强、中、微风化花岗岩层,围岩等级为Ⅲ2~ⅠⅤ2级,该车站地下水类型主要为基岩裂隙水,地下水水量等级贫。车站拱部开挖跨度约22.4 m,高度约7.6 m,矢跨比约为0.34,主体下断面开挖宽度21.1 m,高约10.2 m。车站均位于微风化岩层内,拱顶埋深约14.8~19.9 m,主体结构型式为单拱大跨复合式衬砌结构。

图1 车站概况Fig.1 Station overview
车站施工工法采用初支拱盖法[10-11],通过单层(双层)初期支护形成拱盖结构体系,在其保护下开挖下部岩体,开挖完成后再自下而上顺筑二衬结构。车站施工顺序如图1(c)所示,车站拱部中间分两个台阶开挖,先开挖隧道拱部中间上台阶1部,并施作该部初支拱盖11;与1部相差15.2 m开挖隧道拱部左侧2部,在拱脚位置施作锁脚锚杆12,接长拱顶初支拱盖11,与2部相差15.2 m开挖右侧3部,重复上述工序,完成初支拱盖11施工;在初支拱盖11的保护下,拉槽开挖车站下部岩体,分左、中、右三部分和上、中、下三台阶共9部开挖,并施作相应段的边墙初期支护13,直到开挖到底;自下而上顺筑车站二衬及主体结构,完成车站施工。车站主体结构支护如表1所示。
2 数值计算
2.1 模型及参数
根据地质勘察报告结果,取隧道及四倍跨度的围岩作分析对象,模型尺寸为100 m×75.9 m×45.6 m(宽×高×厚),对Ⅳ2级围岩地层进行简化,进行网格剖分如图2(a)所示,单元数为668 513个,节点数为640 434个。模型的法向位移在前后面和左右面均受约束,底面全位移受约束,上面位移不受约束。围岩采用摩尔-库伦理想弹塑性模型,围岩物理力学参数如表2所示。采用beam单元模拟格栅钢架,采用cable单元模拟预应力锚杆,采用实体单元模拟喷射混凝土,厚度为200 mm,考虑钢筋网对喷射混凝土的增强效应[12],断面支护体系见图2(b),支护结构力学参数如表3所示。为记录隧道全过程施工,选取沿隧道纵向16.4 m处作为监测断面并布置数据监测点,以此来分析隧道施工过程中围岩应力和位移的变化规律[13]。

图2 数值计算模型Fig.2 Numerical calculation model

表1 隧道支护结构参数表Table 1 Parameters of tunnel support structure

表2 Ⅳ2级围岩物理力学参数Table 2 Mechanical parameters of grade Ⅳ2 surrounding rock
2.2 模拟过程
隧道模型开挖方式和支护方式与现场施工保持一致。隧道模型每步开挖进尺0.8 m,并安装预应力锚杆、立架、喷混,隧道模型完全贯通共需288个开挖步序,具体开挖顺序详见1节。隧道代表性施工步序如表4所示。
3 数值模拟结果与分析
3.1 围岩主应力
图3为监测断面各测点[图2(b)]围岩主压力随隧道开挖过程变化曲线,下半部分标识了隧道各部开挖步序。
如图3所示,随着①部导洞掘进逐步靠近监测断面,围岩荷载重分布使得拱顶测点主应力明显增加,其他测点也受影响主应力逐步增加。①部导洞开挖至监测断面时,拱顶测点大、小主应力达到最大值0.72、0.28 MP;断面开挖后,荷载瞬间释放,大、小主应力减少至0.47、0.06 MP;经过断面继续向前推进后,大、小主应力缓慢增加。拱腰测点主应力整体变化规律与拱顶相似。隧道拱部全贯通后,断面拱部各测点主应力无明显变化。
监测断面⑤a部开挖前,受其他导洞开挖影响边墙测点小主应力已缓慢减少,而大主应力快速增加高于初始值。⑤a部开挖后,边墙测点大、小主应力骤减为1.43、0.12 MPa。当⑦a和⑨a部导洞开挖先后通过断面时均会引起边墙测点大主应力显著减小。

表3 支护结构参数Table 3 Support structure parameters
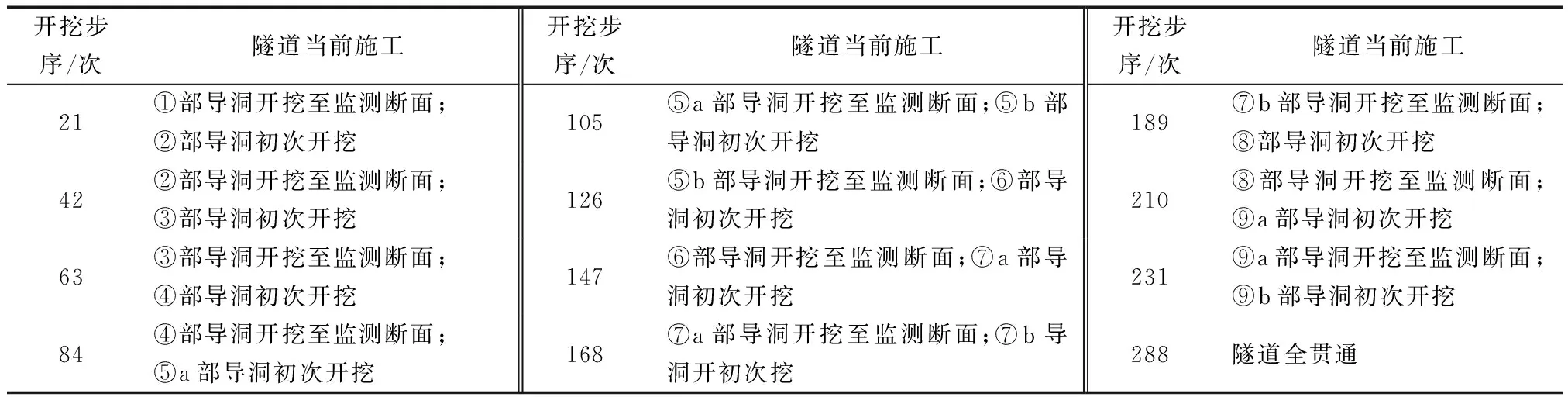
表4 隧道代表性施工步序表Table 4 Typical construction steps of tunnel

图3 隧道开挖过程监测断面各部主应力变化历程Fig.3 Variation history of principal stress at each part of monitoring section during tunnel excavatio
通过以上分析可得:监测断面各测点围岩主应力在开挖过程中表现出先增加超过初始应力达到应力峰值,后释放减小趋于平稳。拱部围岩主应力变化过程受①部导洞开挖影响显著。②、③部开挖对拱顶围岩主应力影响较低。
3.2 围岩强度储备
为了更直观地分析围岩在不同时刻的应力状态,判别围岩是否达到破坏极限[14-15],引入围岩强度储备K,表达式为
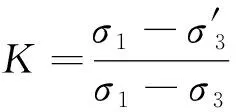
(1)

K越大围岩强度储备越高,当K=1时围岩处于极限状态。图5为监测断面各测点围岩强度储备K随隧道开挖过程变化曲线,图中下半部分标识了隧道各部开挖步序。
如图4所示,拱部各测点K在开挖过程中表现出先逐步下降达到最小值,各部开挖并施加初期支护后上升,最后逐渐降低趋于平稳。受①部导洞开挖影响,各测点围岩大主应力增幅较大、小主应力增幅较小,围岩受力状态变差使得K值下降,且越靠近监测断面越加明显,拱顶尤其突出。断面①部开挖后,开挖面附近围岩由双轴受力转化为近乎单轴受力[16],拱顶K下降到最小值1.55。施加支护结构后,拱顶围岩大、小主应力逐步接近,围岩又转变为双轴受力,K上升明显并在开挖后第5步达到峰值。导洞继续推进后,拱顶K逐步下降趋于稳定。拱腰测点K变化规律与拱顶相似。隧道拱部全贯通后,拱部各测点K再无明显变化。
与拱部测点变化规律不同,⑤a部开挖、施加初期支护后,边墙测点K下降逼近极限状态,后缓慢增加趋于平稳。由于边墙只有少数预应力锚杆和喷射混凝土支护,围岩的三向应力状态未得到足够补偿,导致边墙围岩大、小主应力相差较大,K低于其他部位,需加强边墙支护。
由图5可知,监测断面①部开挖会引起开挖面附近围岩K显著降低,但未有塑性区产生;②部开挖后,右拱腰处产生塑性区,拱腰径向围岩K减小,拱顶K高于其他部位;③部开挖后未产生塑性区,但拱腰径向围岩K继续减小且范围逐步增大;⑤a部开挖后,右拱脚处出现塑性区,此刻边墙位置K已接近极限。隧道全部贯通后,拱顶部位K有所减小,拱腰、边墙部位K有所增大但仍低于拱顶。边墙部位K接近极限,影响深度约为8.9 m。
3.3 隧道位移
图6上半部分为监测断面沉降和水平位移随隧道开挖过程变化曲线,下半部分标识了隧道各部开挖步序。
监测断面拱顶沉降累积过程大致分为3个阶段。①部开挖前,拱顶沉降为增长速率逐步减小的凹曲线;①部开挖后,增长速率开始增大,沉降曲线出现拐点,此时拱顶沉降为4.42 mm占最终值的54.4%;拱部全贯通后,拱顶沉降为8.31 mm占最终值的98.3%,拱顶沉降最终稳定到8.45 mm。
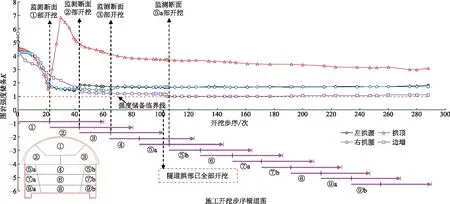
图4 隧道开挖过程监测断面各部围岩强度储备变化Fig.4 Strength reserve change of surrounding rock at each monitoring section during tunnel excavation

图5 监测断面各部塑性区、围岩强度储备K云图Fig.5 Cloud chart of plastic zone and surrounding rock strength reserve K at each part of the monitoring section
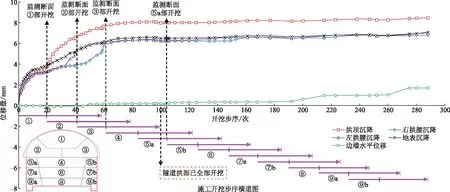
图6 隧道开挖过程断面各部位移模拟数据Fig.6 Displacement simulation data of each section during tunnel excavation
地表沉降主要受隧道拱部开挖影响,整体表现为一条增长速率减少的凹曲线。①部导洞第1次开挖后,地表沉降增至1.55 mm;监测断面①部开挖后,地表沉降为4.03 mm占最终值的57%;拱部全贯通后,地表沉降为6.60 mm占最终值的93.2%,地表沉降最终稳定至7.07 mm。
边墙水平位移变化幅度不大。断面⑤a部开挖后,水平位移增加至0.31 mm,又经过两次阶梯型增加最终稳定在1.70 mm。
拱顶、地表沉降与净空收敛的现场监测数据如图7所示,随时间推移,现场沉降、净空收敛与模拟所得曲线趋势大致相似,位移增长速率发展呈“迅速→平缓”变化特征。由于沉降影响至地表,第80天后,现场隧道拱部至地表呈整体沉降,已充分变形,变化趋势表现一致。监测与模拟数据相差不大,数值与规律比较贴近,拱部开挖完后现场监测和模拟所得曲线均会趋于平稳,后续开挖步序影响较低。
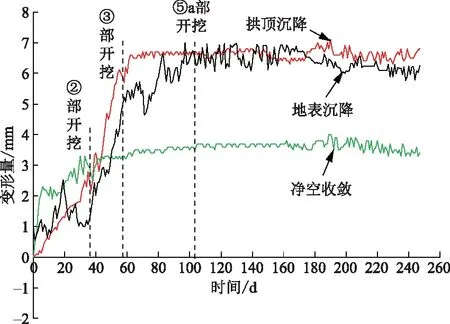
图7 现场监测位移数据Fig.7 Displacement data monitored on site
隧道施工过程中围岩压力的释放规律关系到围岩的稳定性,也决定了隧道位移变化过程的特点。如表5所示,拱顶围岩强度储备最高,其次是拱腰,边墙最低并且有较多塑性区。隧道①部导洞开挖过程引起的拱顶沉降量占比最大;监测断面②、③部扩挖对拱顶沉降影响依次减弱;拱部全贯通后后续开挖基本无影响;地表沉降亦是如此。对于大跨浅埋硬岩隧道,沉降影响至地表,但由于硬岩地层围岩强度高而几乎没有产生塑性区,锚喷格栅初期支护可使隧道达到较高稳定状态。
3.4 支护结构受力
图8为暗挖车站所使用监测仪器及车站现场施工。取监测断面拱顶拱架和锚杆进行掘进过程中受力分析。如图9所示,数值模拟所得的拱架轴力曲线受各部开挖影响明显,各部开挖通过监测断面并施加支护后,拱架轴力上升明显,锚杆轴力无较大变化。拱架轴力稳定在30.74 kN,锚杆轴力稳定在102.17 kN。结合现场监测数据,两者拱架、锚杆轴力曲线变化趋势大致相同,各部开挖通过监测断面时均会造成拱架轴力发生突变,但对锚杆轴力无明显影响,现场围岩侧和临空侧拱架轴力分别为12.55、17.92 kN,锚杆轴力为108.22 kN。总体上看,两者拱架轴力在同一数量级,锚杆轴力相差较小,拱架受力小,锚杆预应力损失小。断面各部开挖时均会造成拱架轴力发生增加,但增量随掘进过程逐渐降低。

表5 监测断面各部围岩强度储备、塑性区、沉降对比Table 5 Comparison of strength reserve, plastic zone and settlement of surrounding rock at each monitored section

图8 现场监测仪器及车站施工图Fig.8 Site monitoring instrument diagram and station construction drawing
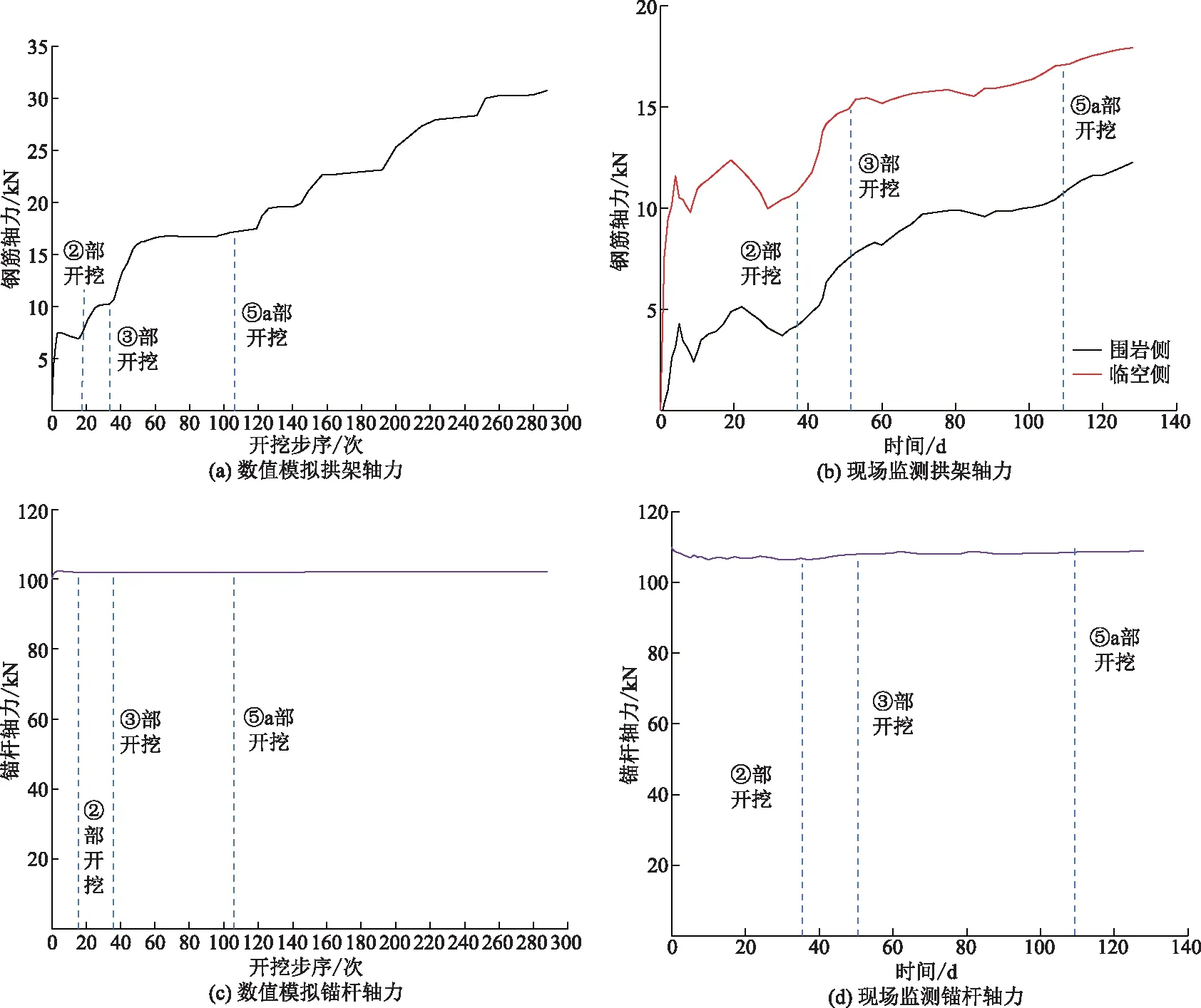
图9 数值模拟、现场监测支护结构受力图Fig.9 stress diagram of support structure through numerical simulation and field monitoring
4 结论
(1)监测断面各测点围岩主应力在开挖过程中表现出先增加超过初始应力达到应力峰值,后释放减小趋于平稳。①部导洞开挖造成的围岩主应力变化最为明显,使开挖面附近围岩强度储备显著降低。②、③部导洞开挖对拱顶主应力扰动较小。
(2)①部导洞引起拱顶及地表沉降量占最终值的54%和56%,②、③部导洞开挖对拱顶及地表沉降影响依次减弱,后续施工影响更小。从总体过程来看,①部导洞开挖对隧道沉降控制最为关键。
(3)隧道全贯通后,拱顶围岩强度储备为3.1,拱腰为1.78,边墙为1.1接近极限状态。从隧道各部位围岩强度储备角度上看,边墙最为关键需支护。
(4)地铁暗挖车站虽跨度大、埋深浅,但由于硬岩地层围岩强度高而几乎没有产生塑性区,锚喷格栅初期支护即可使隧道达到较高的稳定状态。
