基于有限元的不同内圈结构关节轴承径向承载分析
2017-11-21

摘要: 针对宽内圈关节轴承端部台阶处容易出现应力集中而发生开裂的问题,对GEW12型关节轴承的宽内圈提出4种不同的结构形式,利用有限元法分别对其进行轴承径向受载分析,讨论结构变化对等效应力、第一主应力和整体结构位移的影响。试验测试和仿真分析结果认为:在内孔端部倒角为0.2 mm或倒圆角为1.0 mm时,宽内圈容易产生应力集中而导致开裂,而内孔端部倒斜角或沉槽5.0 mm×0.5 mm的结构未发生失效,故后者可作为宽内圈结构设计的较优选择形式。
关键词: 宽内圈; 径向加载; 等效应力; 主应力; 位移; 有限元
中图分类号: V229.2 文献标志码: B
Radial loading analysis on spherical plain bearing with different inner ring structure based on finite element
LIN Zhixun
(Fujian Longxi Bearing(Group) Co., Ltd., Zhangzhou 363000, Fujian, China;
Fujian Provincial Key Laboratory of Spherical Bearing, Zhangzhou 363000, Fujian, China)
Abstract: Spherical plain bearings with extended inner ring are very likely to have cracks on their shoulders due to stress concentration. To solve this problem, the GEW12 bearing is studied with four different extended inner ring structures, and radial loading analysis are carried out for the bearing with finite element method. The influences on equivalent stress, major principal stress and overall structural displacement according to the structure changes are discussed. The test and simulation results show that, if the inner chamfer is 0.2 mm or the fillet is 1.0 mm, the extended inner rings are very probable to show cracks on their shoulders due to stress concentration; while the structure is still working when the inner chamfer or sinking groove is 5.0 mm×0.5 mm, the latter one should be considered as a better choice for the design of extended inner rings.
Key words: extended inner ring; radial loading; equivalent stress; principal stress; displacement; finite element
0 引 言
自润滑关节轴承是一种无须补充润滑剂的特殊关节轴承,相比普通关节轴承,其内圈和外圈之间的球面接触副上镶有自润滑材料,在工作中可产生自润滑效果,具有优异的工作特性,故广泛应用于工程机械、载重汽车、水利设施、建筑路桥、航空航天、军工装备等领域。[1-2]相比国外同类产品而言,国内在该产品的研究和开发上起步较晚,基础薄弱,产品的性能和质量不太稳定,目前航空领域所使用的高性能、长寿命自润滑关节轴承仍需要依靠进口。[3]近年来,随着航空工业的迅速发展,航空自润滑关节轴承的市场需求逐渐扩大,国内轴承制造厂商和研究单位投入大量的人员和经费进行研发,争先恐后地赢取市场先机。
通常,航空自润滑关节轴承和建筑路桥关节轴承主要围绕强度和寿命2个方面进行选型和使用,对应的失效模式同样存在强度失效和磨损失效2种情况。[4]在强度分析方面,国内许多研究者采用有限元方法对自润滑关节轴承的受载进行力学性能分析[5-6],通过改变轴承结构尺寸进一步优化得到最佳轴承结构[7];在寿命计算方面,目前大多基于试验测试和实践经验总结得出的估算公式计算而得[8]。
与普通关节轴承相比,宽内圈关节轴承在结构上有一个显著特点,即内圈两端带有圆柱形台阶,且整体内圈宽度比普通关节轴承宽50%以上。GEW12型宽内圈自润滑关节轴承结构见图1。
在使用时,宽内圈两端的台阶虽然能够取代常用的垫圈在轴向上起到约束作用,但其同时给结构受力带来弊端,这类轴承宽内圈在受到较大的径向载荷作用时,容易在台阶处发生应力集中而造成开裂。[9]为合理解决这一问题,对GEW12型关节轴承的宽内圈提出几种不同的结构形式,在具有相同外形尺寸的条件下,对其径向承载能力进行有限元分析,并结合试验验证,总结得出较为合理可靠的宽内圈结构。
1 宽内圈的不同结构形状特点
为对比分析,选取GEW12型关节轴承的宽内圈作为研究对象,将该型号宽内圈4种常见的内孔结构形状分别命名为A,B,C,D型(见图2),且4种结构的外形尺寸均一样,球径为25.4 mm,内孔直径为12.7 mm,内圈宽度为24.0 mm,主要区别在于:A型和B型在內孔两端分别做0.2 mm倒角和倒圆角1.0 mm;C型在内孔做较大的倒斜角5.0 mm×0.5 mm;D型在内孔两端开沉槽5.0 mm×0.5 mm,且沉槽底部倒斜角0.5 mm×45°。针对这4种不同结构,利用Abaqus软件进行有限元建模分析,观察轴承在径向受载时其内部的应力、位移分布情况,从而判断出轴承的危险部位或可能开裂的地方,为轴承的结构设计和优化提供理论参考。endprint
2 有限元建模分析参数设置
GEW12关节轴承属于向心结构,主要承受径向载荷作用,本文以轴承的径向极限承载试验作为检验内圈承载性能的方法,采用Abaqus对其进行有限元建模分析[10],轴承径向加载试验示意见图3。为减少模型的网格数量,提高计算效率,根据结构的对称性特点选用几何模型。该模型主要由轴承内圈、外圈、芯轴、加载板、支座组成,各零部件的材料属性为弹塑性,具体材料参数见表1。模型网格全部采用六面体网格,对局部应力集中处进行加密处理,单元类型为C3D8R,网格总数约为28万个。
载荷边界条件为:支座底部施加固定约束,模型对称面施加对称约束,加载板顶部施加极限载荷70 kN。各零部件之间的接触面均设置为面-面接触对,切向力选择库仑摩擦模型,摩擦因数取为0.12。
3 有限元分析结果
3.1 不同结构形状对内圈等效应力分布的影响
4种不同内孔结构宽内圈在径向极限静载荷作用下的等效应力分布云图见图4,对应的应力最大值见表2。
A型和B型的等效应力分布规律类似,即:宽内圈上半部分主要承载区域应力数值较大,两端台阶区域呈深红色,等效应力水平在1 300 MPa左右;中间厚壁大部分区域呈绿色,等效应力水平约为750 MPa,蓝色局部区域应力数值较小;内孔表面中心位置出现浅红色,其平均等效应力约为1 100 MPa;下半部分基本呈现深蓝色,表明该区域的等效应力很小,数值趋近于0。
C型和D型结构的宽内圈等效应力分布规律相似,上部承载区域应力水平较高,下部蓝色区域应力水平较低。C,D型与A,B型区别之处在于:C,D型内圈的端部台阶应力显著下降,外倒角呈蓝色,说明应力趋近于0;内孔倒角应力集中部位向中心位置转移,最大等效应力位置仍发生在倒角根部,数值明显增大。
由此可知,当宽内圈的承载接触宽度发生改变(由24.0 mm减小到14.0 mm)时,等效应力集中区域由内孔端部向内侧转移,且最大等效应力数值随之增大,这表明在相同径向载荷作用时,内孔接触面积越小,接触区域端部特别是倒角根部,等效应力集中越严重。此外,由于芯轴和内圈在受载时存在弯矩作用,中间部分发生不同程度的挠曲变形,使得内孔接触表面的等效应力分布由外向内减小。
3.2 不同结构形状对内圈主应力分布的影响
不同结构宽内圈在极限径向静载荷作用下的第一主应力分布云图见图5,对应主应力最大值见表3。
3.3 不同内圈结构对外圈受力的影响
不同内圈结构的轴承外圈受力分析结果见图6。由于内圈的结构变化对外圈的应力分布影响很小,故选一种外圈为代表进行分析。外圈红色区域为径向受压部位,应力水平高,最大等效应力为795.2 MPa,略微超过材料的屈服强度793 MPa,表明径向极限静载荷时外圈发生微量的塑性变形,最大等效塑性应变仅为0.182%。但是,外圈最大应力远未达到抗拉强度965 MPa,而且外圈延伸率高,塑性硬化作用强,在一定程度上仍可抵挡更大的径向载荷作用而不发生破坏。总之,尽管宽内圈的内孔结构形状发生变化,但其并不改变外圈的受力承载面积,所以4种不同结构内圈的轴承在相同载荷作用下的等效应力和等效塑性应变分布基本相同。
3.4 不同内圈结构对承载结构刚度的影响
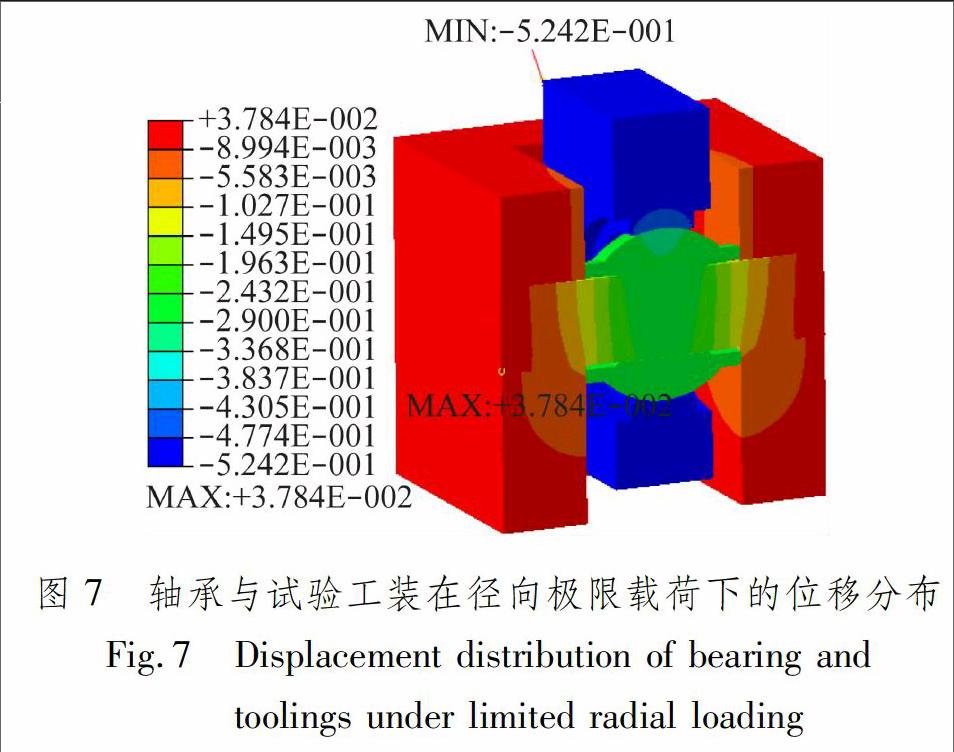
在径向极限载荷作用下,轴承与试验工装的位移分布见图7。红色区域表示基本静止不动的部位,绿色和蓝色区域分别表示向下位移较小和较大的区域,位移绝对值最大位置出现在加载板顶部。芯轴中间部位比两侧受支撑部位的变形要大,中间发生一定程度的向下挠曲变形。
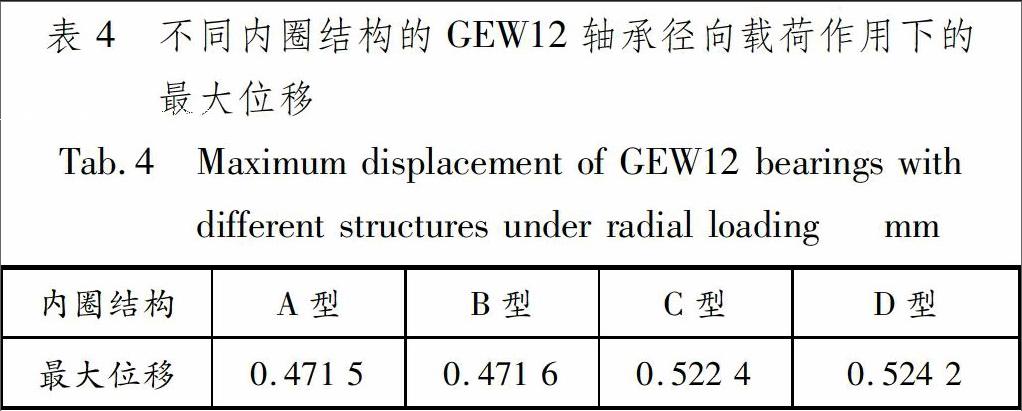
4种不同内圈结构的轴承在相同载荷作用下的最大位移见表4。沿加载方向的加载板最大位移值按照A,B,C,D的顺序依次增大,其中A,B型内圈结构的轴承位移值相近,C,D型内圈结构的轴承位移值也相近,表明轴承内孔的承载宽度或接触面积越大,结构的刚度越好,整体位移变形量越小。
4 极限承载试验结果对比
为对比不同内圈结构的轴承径向承载能力,根据SAE AS81820D标准[12]开展径向极限加载试验,观察轴承内圈在受载时是否出现破裂现象。为确保试验数据的可靠性,不同内圈结构的轴承产品均在相同工艺条件下加工,每种内圈结构各取3套样品进行测试。试验设备采用CMT5105电子式万能试验机,施加最大载荷为轴承径向极限静载荷140 kN,加载速率为1 kN/s。试验得到的A,B,C,D型内圈结构轴承的测试结果见表5,其中位移量由位移传感器测量加载板底面的數值并取无破裂样品数值进行平均计算后得到。
从位移结果来看,试验所得数值与表4仿真分析结果相比,两者较接近,且前者要小于后者约0.03~0.06 mm。造成偏差的原因主要是仿真模型在参数设置时进行简化,与实际条件存在一些偏离。尽管如此,仿真分析结果仍具有较高的可信度,能够用来指导实际工作,可体现出理论分析的价值。
由破裂情况可知:A,B型内圈端面个别样品在载荷未达到140 kN前就出现端部破裂现象(见图8);C,D型内圈样品均能承受极限载荷140 kN的作用而完好无损。结合第3.1和3.2节的仿真分析结果,发现A,B型内圈的端部台阶部位出现较大的应力集中现象,应力数值超过材料的屈服强度,且端部高应力区外围表面呈现开放状态,比C,D型内圈高应力区外围受包容状态更恶劣,更加容易引起裂纹的萌生和扩展。由此可见,仿真分析可根据受载工况的应力分布状态,准确判断轴承结构的应力破坏位置,从而指导产品设计和结构优化。
5 结 论
在相同径向载荷作用下,当内圈内孔接触面宽度减小时,若结构由A,B型变为C,D型,则:等效应力集中部位由内圈的台阶处向内孔中间部位转移,应力最大值均出现在内孔倒角根部,但数值会有所增大;第一主应力最大区域由外倒角处向球面与台阶交界处转移,主应力最大值显著降低;轴承结构的变形略有增大,刚度有一定程度的降低。endprint
结合应力分布和试验结果可知:A,B型宽内圈薄弱之处在端部台阶的外倒角处,径向极限承载试验时发生内圈端部破裂现象;C,D型宽内圈在球面与台阶的交界处主应力较小,试验时未发生内圈破裂现象。内圈受载破裂的概率由大到小顺序为B,A,D,C,显然轴承在径向承载时宽内圈内孔结构以C型最为合理。内圈的内孔结构变化,不会改变外圈内球面的承载面积,外圈整体应力和应变分布基本保持不变。
参考文献:
[1] 杨育林, 祖大磊, 黄世军. 自润滑关节轴承现状及发展[J]. 轴承, 2009(1): 58-61.
YANG Y L, ZU D L, HUANG S J. Status and development of self-lubricating spherical plain bearings[J]. Bearing, 2009(1): 58-61.
[2] 何两加. T型自润滑关节轴承介绍[J]. 机械工程师, 2011(4): 127-128.
HE L J. T type self-lubricating spherical plain bearings[J]. Mechanical Engineer, 2011(4): 127-128.
[3] 杨昆, 林晶. 国外航空自润滑关节轴承标准分析[J]. 航空标准化与质量, 2013(5): 45-49.
YANG K, LIN J. Analysis on the standards of self-lubricating spherical plain bearings used in international aviation[J]. Aeronautic Standardization & Quality, 2013(5): 45-49.
[4] 贺东斌, 冯元生. 航空关节轴承的可靠性分析[J]. 机械强度, 1995, 17(1): 29-31. DOI: 10.16579/j.issn.1001.9669.1995.01.008.
HE D B, FENG Y S. Reliability analysis for spherical plain bearing[J]. Journal of Mechanical Strength, 1995, 17(1): 29-31. DOI: 10.16579/j.issn.1001.9669.1995.01.008.
[5] 王兆昌. 擠压型铝合金自润滑关节轴承性能研究[J]. 轴承, 2015(8): 36-40.
WANG Z C. Study on performance for self-lubricating spherical plain bearings extruded in aluminum alloy[J]. Bearing, 2015(8): 36-40.
[6] 胡宝根, 王卫英, 岳琳琳. 基于有限元法的自润滑关节轴承静力学分析[J]. 轴承, 2014(4): 10-13.
HU B G, WANG W Y, YUE L L. Statics analysis of self-lubricating spherical plain bearings based on FEM[J]. Bearing, 2014(4): 10-13.
[7] 王世超, 王秀梅. 基于ANSYS的自润滑关节轴承结构改进分析[J]. 工业控制计算机, 2014(9): 114-115.
WANG S C, WANG X M. Structure optimization and analysis of self-lubricating spherical plain bearing based on ANSYS[J]. Industrial Control Computer, 2014(9): 114-115.
[8] 李科委, 沈雪瑾, 陈有光, 等. 衬垫自润滑关节轴承研究现状与展望[C]// 第八届全国摩擦学大会论文集. 广州, 2007: 171-176.
[9] 段宏瑜, 刘红宇, 朱淋淋. 基于Workbench的自润滑关节轴承失效分析及优化设计[J]. 轴承, 2016(9): 52-56.
DUAN H Y, LIU H Y, ZHU L L. Failure analysis and optimal design for self-lubricating plain bearings based on Workbench[J]. Bearing, 2016(9): 52-56.
[10] 石亦平, 周玉蓉. Abaqus有限元分析实例详解[M]. 北京: 机械工业出版社, 2006: 165-207.
[11] 刘鸿文. 材料力学[M]. 4版. 北京: 高等教育出版社, 2004: 212-253.
[12] Bearings, plain, self-aligning, self-lubricating, low speed oscillation: AS81820D[S].endprint
